着眼常规 揭示本质 聚焦核心素养
——例谈一道中考试题的解法
◎秦贵平 (湖北省长阳土家族自治县龙舟坪学区,湖北 宜昌 443501)
为进一步体现学业水平考试的选拔功能,压轴综合性试题必不可少,这类题往往综合性极强,考生不容易找到解题的突破口,无从下手,导致得分率低.解决这一类问题,往往需要学生有较强的综合能力和数学素养,找准“题眼”和切入点是解题的关键.
1.试题呈现
(2017年湖北襄阳市中考试题)如图1,矩形OABC的两边在坐标轴上,点A(10,0),抛物线y=ax2+bx+4过B,C两点,且与x轴的一个交点为D(-2,0),点P是线段CB上的动点,设CP=t(0 (1)请直接写出B,C两点的坐标及抛物线的解析式; (2)过点P作PE⊥BC,交抛线于点E,连接BE,当t为何值时∠PBE=∠OCD? (3)点Q是x轴上的动点,过点P作PM∥BQ,交CQ于点M,作PN∥CQ,交BQ于点N.当四边形PMQN为正方形时,请求出t的值. 问题(1)(2)学生一般没有思维障碍,能够顺利解答,本文不再赘述.问题(3)以二次函数为背景,综合考查四边形、二次函数相关知识,命题者在这里设置了P、Q两个“动点”,两个点同时运动导致了图形并不唯一存在,综合考查了四边形、三角形、二次函数相关知识.因此,透过题目表象,如何在运动中求静,即探索动点静止时的特殊位置、特殊图形变成了本题的解题关键.基于此,本文从“模型思想”和“辅助圆”两个视角出发,探究解题路径,寻求直接、自然的解答. 本题实则是在运动中探究特殊四边形的存在性问题,从特殊图形存在性问题的一般处理策略看,我们都是先假设存在,然后根据图形的定义、性质来解决问题本身.因此,如何确定动点的位置,是解决这一类问题的关键.此题中,四边形PMQN已经是平行四边形,那么如何才能使四边形PMQN是正方形呢?我们常规第一反应就是直角,构造“一线三等角”模型,那么此题中如何确定这个直角便成了解决本题的关键?我们注意到矩形COAB,因此我们从∠CQB入手,如果∠CQB是直角,那么一箭双雕.一方面,通过构造“K”图相似,确定点Q的位置;另一方面,平行四边形PMQN成了矩形,这样只需一组邻边相等便可以解答此题. 解法1如图2,假设四边形PMQN为正方形,则: ∠PMC=∠PNB=∠CQB=90°,PM=PN. ∴∠CQO+∠AQB=90°. 又∵∠CQO+∠OCQ=90°, ∴∠OCQ=∠AQB, ∴Rt△COQ∽Rt△QAB, 设OQ=m,则AQ=10-m ∴m(10-m)=4×4,解得:m1=2,m2=8. 题中有两个动点P、Q,加之图形复杂,含参量多,计算量大,令很多考生望而生畏.通过上述解答,我们发现表面上运动的Q点实际上只有两个点,为什么呢?我们冷静下来认真读题、审题,挖掘题中的关键信息和条件,这些条件背后隐含的数学本质是什么,与题中所求解的结论有什么联系,层层剖析,重点突破关键信息,动中求静,我们产生以下第二种思考. 解法2如图3,以CB为直径构造⊙H与x轴交于点Q,连接HQ, 过点H作HF⊥x轴于点F,得HF=4,HQ=5. ∴OQ=OF-QF=2. “圆”是中学数学中必须掌握的重要知识,构造“辅助圆”是解决相关数学问题的重要方法.在解题教学中,如果能根据题设和已知条件构造符合题意特征的辅助圆,这样将题中的固定角转化成圆周角,使得问题顺利解决,同时也体现了一种数形结合思想,代数问题和几何知识互相渗透,综合应用,不仅能够更好地解决问题,还能更好地培养学生分析问题的能力.虽“图中无圆”但必须做到“心中有圆”,教师应帮助学生体会 “‘圆’来可以更简单”的喜悦. 无独有偶,笔者在收集各地中考试题时,发现2020年襄阳中考试题再现“辅助圆”.可见在平时的解题教学中,要注重好的、常见方法的积累.要真正领悟某一类题型的类型和处理策略,从而达到“会当凌绝顶,一览众山小”的境界,这需要长期的积累和内化. 试题再现:(2020年襄阳市中考试题)在△ABC中,∠BAC=90°,AB=AC,点D在边BC上,DE⊥DA且DE=DA.AE交边BC于点F,连接CE.探究证明:当AD≠AF时,请探究∠ACE的度数是否为定值,并说明理由.(结合本文讨论主题,题目有删减.) 此题常规性方法,容易想到用相似解决.但是倘若能够抓住∠AED=∠ACD,∠ADE=90°这两个关键信息,构造如图所示的“辅助圆”,问题迎刃而解.具体解答过程,本文不再赘述. 解题是一位数学教师专业成长中必须经历的一个重要过程,是数学教师的基本功.但教学的终极目的是发展学生,如何通过教师的影响让学生形成解题能力才是关键.很多时候,老师们都有这样的抱怨:“为什么某个题讲了很多遍学生还不会呢?”裴光亚先生说:“数学教学是数学活动的教学,是师生之间、学生之间的交往互动与共同发展的过程”,我想这是对这一“抱怨”的最好解释,也许很多时候我们真的只是做了一个参考答案的“搬运工”.换个角度,也许很多时候忽略了一个问题:学生是不是真正参与了整个解题的思维过程?如本题中,学生若对特殊四边形存在性问题的处理策略没有形成自己的经验,可能就会无从下手.在平日教学里,教师要以“教学资源”为背景,让学生充分感知思维过程,这样的教学活动多了,学生便会积累成基本经验,进而形成能力. 早在先秦时代,我国著名古籍《礼记》就提出“学然后知不足,教然后知困.知不足然后能自反也,知困然后能自强也.”这个观点的核心就是教学相长,要做到这一点并非一件容易的事情,首先教师自身要有扎实的专业功底,有前沿的教育理念,有开阔的教学视野.教学是一个双向选择的过程,单靠教师个人的“功夫”是远远不够的.笔者曾经也有这样的困惑,经常会出现自我认为课堂讲得非常精彩,学生也听得非常认真,甚至沾沾自喜,自我陶醉的感觉,可学生成绩没有得到提升,这是因为教师在很多时候只关注了“讲”和“教”,忽视了教育对象的学习状态.我们还应更多地走下讲台,多站在学生的角度思考,他们怎么看待问题.教学不仅是简单的知识传授,更多地还要关注思维的启发,要尽可能地达到“解一题,通一类”的效果. 裴光亚先生把教师的教学分为三种境界,六个层次,教师的成长,必须经历从经验型教师到研究型教师的跨越,经历从初师到大师的跨越.教学是一个发现学生、发展学生,发现自我、发展自我的过程,是师生共度的生命历程.[1]聚焦核心素养,整合教学资源,揭示知识板块之间的联系,形成数学思维和素养是每一位教师追求的至高境界. 函数及其思想方法是整个数学学习的重头戏,中学阶段函数很好地解释了运动和变化这一数学精髓,用数的形式更好地揭示了数学的“内在本质”和图形的“外在美”.因此用函数作为载体,综合几何问题,搭建运动变化的平台成了命题者的一个最好选择.回看各地中考试题,压轴综合题不是呈现某一个难点知识,这类题往往都是多个知识点、多种思想方法的综合体,既考查教材所要求的方程思想、代数运算、几何性质,又考查考生灵活运用这些知识解决问题的能力.因此在教学中,教师除了注重知识的讲授以外,还应该注重提炼重要的思想方法,挖掘试题考查的本质,总结与之对应的处理策略,发展学生能力,发展教师自我,达到共赢境界,始终盯准数学核心素养的提升.2.试题分析
3.解法探究
3.1 常规出发,寻求自然
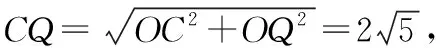


3.2 抓住本质,探求直接
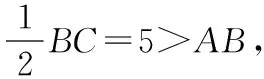

3.3 举一反三,拓展延伸
4.解后反思
4.1 着眼常规,通性通法,积累活动经验
4.2 盘活课堂,教学相长,打造高效课堂
4.3 揭示本质,发展能力,聚焦核心素养

