浅谈矩阵秩的求法

◎薛丽娜 (太原广播电视大学，山西 太原 030000)

矩阵的秩是刻画矩阵特征的重要参数，矩阵秩的求解和应用对学生而言也是重中之重，以下结合实例介绍矩阵秩的几种常用的求解方法：定义法、初等变换法、转换为向量组的秩求解和分块矩阵法.

1 定义法

定义：矩阵A的非零子式的最高阶数称为矩阵A的秩，记为r(A)或秩(A).

定义法求矩阵的秩适用于阶数较小的矩阵.求解方法即在矩阵A中寻找非零的r阶子式(存在即可)，且高于r阶的子式均为零 ，则称r为矩阵A的秩.

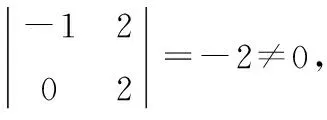
2 初等变换法

矩阵的初等变换(行变换和列变换)不改变矩阵的秩，故可通过初等变换将矩阵简化为阶梯矩阵，阶梯矩阵非零行的行数即为矩阵的秩.

解将矩阵A进行初等变换：

由上述可知矩阵A经过初等变换转化为非零行数为1的阶梯矩阵，因此r(A)=1.

3 转化为向量组的秩

所谓矩阵的行秩就是指矩阵的行向量组的秩；矩阵的列秩就是矩阵的列向量组的秩.

矩阵的行秩与列秩是相等的，统称为矩阵的秩.因此求解矩阵的秩可以转化为求解矩阵向量组(行向量组或列向量组)的秩，即求向量组极大线性无关组所含向量的个数.

令k1α1+k2α2=0，即k1(1,-1,0,0)′+k2(-1,2,1,1)′=(k1-k2,-k1+2·k2,k2,k2)=(0,0,0,0)，

可得k1=k2=0，因此向量α1与向量α2线性无关.

再令k1α1+k2α2+k3α3=0，即

k1(1,-1,0,0)′+k2(-1,2,1,1)′+k3(0,1,1,1)′=(k1-k2,-k1+2·k2+k3,k2+k3,k2+k3)=(0,0,0,0)，

可得k1=k2=1，k3=-1，因此向量α1、α2和α3线性相关.

同理可得向量α1、α2和α4线性无关，α1、α2和α5线性无关，α1、α3和α4线性无关，α1、α3和α5线性无关，α1、α2、α3和α4线性相关，α1、α2、α3和α5线性相关，α1、α2、α4和α5线性相关，α1、α3、α4和α5线性相关，α2、α3、α4和α5线性相关，因此矩阵A的秩为3，即r(A)=3.

4 分块矩阵法

对于复杂的高阶矩阵，上述几种方法并非最优的解决办法，在此介绍分块矩阵法可使高阶矩阵的秩的求解变得更加简单，分块矩阵法主要利用降阶的思想.

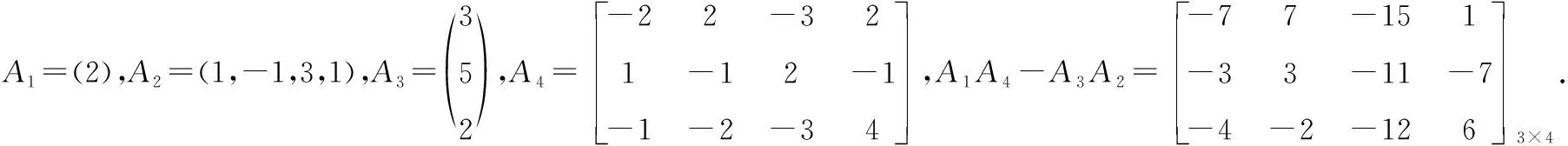
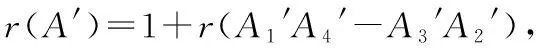
代入矩阵：

故r(M)=2.

以上几种方法的介绍，能帮助学生较好地理解求矩阵秩的基本方法.对于阶数较小的数字矩阵优先采取定义法、初等变换法或转化为向量组的秩进行求解，对于阶数较高的复杂矩阵优先采用分块矩阵法进行求解，熟练掌握这些方法会达到事半功倍的效果.