α阶右侧Caputo分数阶导数的高阶插值逼近
闫羽媛,梁宗旗
(集美大学理学院,福建 厦门 361021)
0 引言
分数阶微积分理论及其数值逼近是数学的一个重要分支,它是传统的整数阶微积分理论的推广。近年来,分数阶微分方程及其应用得到了广泛的关注,其主要归因于分数阶微积分理论自身的迅速发展及其在数学、物理、信号和图像处理等各学科中的广泛应用。分数阶微分方程是广义非整数阶的微分方程,它能获取在时间和空间上具有幂律内存内核的非局部关系,为描述不同物质的记忆和继承性质提供了强有力的工具。研究这类方程具有明确的物理背景,同时也开启了分数阶微分和积分方程理论方面的研究。分数阶微分方程适用于描述现实世界中具有记忆以及遗传性质的物理行为或材料问题,因而更广泛地应用于反常扩散、粘性力学、流体力学、信号处理等领域。在实际求解中,分数阶微分方程的解析解很难显式给出,即使是线性分数阶方程的解析解,也大多含有一些特殊函数,而这些函数的计算本身相当困难。所以,如何构造高效的数值方法来模拟分数阶微分方程是当今最热门的研究课题。关于分数阶导数,现在有几种不同的定义,如空间分数阶Laplace算子[1-2]、Riesz空间分数阶导数[3]等。大多数文献中涉及的Riesz分数阶导数均为Riemann-Liouville框架下的分数阶导数。但Pandey等[4]指出,Caputo定义能够避免一些分数阶导数存在的质量守恒误差、超奇异反常积分、常数的导数非零、初始条件中的分数阶导数无直观的物理意义等问题。分数阶导数定义为在Caputo意义下的Riesz分数阶导数,也称为Riesz-Caputo分数阶导数[5]。
Caputo分数阶导数分为左侧导数和右侧导数。左侧Caputo分数阶导数的离散主要是L1和L2离散:Murio[6]对α阶(0<α<1)Caputo型时间分数阶低扩散方程作L1离散建立差分方程,其截断误差为O(Δt);Lin等[7]也类似地利用L1离散,并将精度提高到O(Δt2-α);Sun等[8]构造了L1-2格式进行离散,并证明其收敛阶O(Δt3-α);Du等[9]改进L1-2格式为一致的L2格式,对α阶(1<α<2)左侧Caputo分数阶导数进行离散,得到了一致的O(Δt4-α)精度。杜瑞莲等[10]对α阶(0<α<1)右侧Caputo分数阶导数作L2-1插值逼近,并证明其收敛阶为O(Δt3-α)。为了得到Riesz-Caputo分数阶导数的高阶格式,需要研究α阶(1<α<2)右侧Caputo分数阶导数的数值逼近格式。本文主要构造了α阶(1<α<2)右侧Caputo分数阶导数的一种高阶数值逼近格式,通过引入新变量,先用L2-1格式构造数值离散,进一步改善得到一致的L2逼近格式,并给出其严格的误差估计,证明了收敛阶为O(Δt4-α)。
1 右侧Caputo分数阶导数的L2-1格式
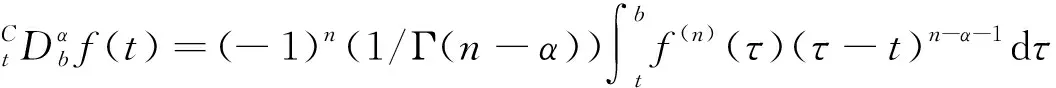
根据右侧Caputo分数阶导数的定义知,当α=n-1时,该导数退化为一般形式的整数阶导数。为方便起见,本文只讨论1<α<2的情况。
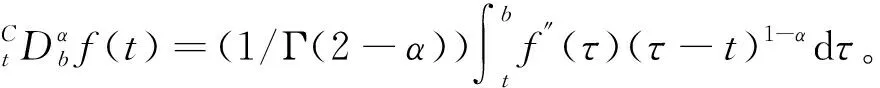
假设g(t)∈C3[t,b],记t=tk (1) 将式(1)中区间[tj-1,tj](j∈[k+1,N-1])上用L2插值P2,jg(t)来近似代替g(t),区间[tN-1,tN]上用L1插值P1,Ng(t)来近似代替g(t),P2,jg(t)=g(tj-1)(tj-t)(tj+1-t)/(2Δt2)+g(tj)(t-tj-1)(tj+1-t)/Δt2+g(tj+1)(t-tj)(tj-1-t)/(2Δt2),P1,Ng(t)=g(tN-1)(tN-t)/Δt+g(tN)(t-tN-1)/Δt,对应的截断误差分别为:g(t)-P2,jg(t)=g‴(ζi)(t-tj-1)(t-tj)(t-tj+1)/6,t∈[tj-1,tj],ζi∈(tj-1,tj+1),g(t)-P1,Ng(t)=g″(ξ)(t-tN-1)(t-tN)/2,t∈[tN-1,tN],ζ∈(tN-1,tN)。 式(1)中右侧α阶(1<α<2)Caputo分数阶导数可以写为: (2) 其中: (3) 注意到, (4) (5) (6) 其中:bl=l2-α-(l-1)2-α,1≤l≤N-k;el=((l-1)3-α-l3-α)/(3-α)+(3(l-1)2-α-l2-α)/2;l≥1。 将式(4)~式(6)代入式(2)中得, (7) 引理1当N≥k+3时,对于任意的α(1<α<2),式(7)中系数wl有下列性质:1)wN-1>|wN-2|;2)wl>0,l≠N-2;3)wN-1>wN-3;4)wN-3≥wN-4≥…≥wk。 证明根据wl的定义及ej、bj的性质,易得1)~3)。下面证明性质4)。 当k+1≤l≤N-3时,wl=eN-l-1+bN-l-1-eN-l=[(N-l-2)3-α-2(N-l-1)3-α+(N-l)3-α]/(3-α)+[(N-l-2)2-α-2(N-l-1)2-α+(N-l)2-α]/2。 令w(x)=[(x-1)3-α-2x3-α+(x+1)3-α]/(3-α)+[(x-1)2-α-2x2-α+(x+1)2-α]/2,则有w′(x)=[(x-1)2-α-2x2-α+(x+1)2-α]+(2-α)[(x-1)1-α-2x1-α+(x+1)1-α]/2。 令h(x)=x2-α+(2-α)x1-α/2,则w′(x)=h(x-1)-2h(x)+h(x+1)。由于h″(x)=(2-α)(1-α)x-α+(2-α)(1-α)x-α-1/2=(2-α)(1-α)(x-α-(α/2)x-α-1)<0,故h(x)是一个凸函数。根据凸函数的性质得h(x-1)-2h(x)+h(x+1)>0。特别地,当x=N-l-1时,w′(N-l-1)=h(N-l-2)-2h(N-l-1)+h(N-l)>0。证毕。 为了研究式(7)中的系数,引入引理2。 引理2假设f(t)∈C4[t,b],记fj=f(tj)。当N≥k+3时,则有: (8) (9) (10) 证明先讨论k+1≤j≤N-2的情况。应用Taylor展开式, (11) (12) (13) (14) 注意到, (15) (16) (17) (18) (19) (20) 利用引理2,当N≥k+3时,式(7)变为 (21) 其中, Rk+1/2=O(Δt4-α)+(Rk+Rk+1)/2。 (22) 在式(21)中,系数dk的具体形式如下: |Rk+1/2|≤(1/Γ(2-α))[((6-α)(α-1)/(6(2-α)(3-α)(4-α))-1/12) (23) 证明由式(3)有, (24) 其中, (6-α)/(6(2-α)(3-α)(4-α))f(4)(ζk)Δt4-α,ζk∈(tk,tk+2)。 (25) (26) (27) 定理1中的式(23),由于在区间[tN-1,tN]上采用L1插值,其整体误差不是一致的O(Δt4-α)格式。实际计算中该区间上的误差对整体误差不会产生较大的影响,为此本节将利用L2在区间[tN-1,tN]上作插值逼近,使其整体误差得到一致的O(Δt4-α)精度。 假设函数f(t)在区间[tk,tN+1]上有定义,可以在每一个小区间[tj-1,tj](j≥k+1)上均利用二次插值多项式P2,jg(t)逼近函数g(t)。 (28) 其中, (29) (30) s2-αds+[(N-k-1)3-α-(N-k)3-α]/2|≤C(N-k)2-α,C是一个正常数。可以得到 (31) 其中, (6-α)/(6(2-α)(3-α)(4-α))f(4)(ζk)Δt4-α,ζk∈(tk,tk+2), (32) (33) 本文先利用L2-1格式对α阶(1<α<2)右侧Caputo分数阶导数进行插值逼近,并讨论了其系数性质。为了改善由L1插值在区间[tN-1,b]上带来的缺陷,进一步提出L2插值逼近格式,通过增加一定的限制条件,得到了一致的O(Δt4-α)阶精度,并分别对二者的截断误差进行估计。基于上述推导,本文提供的是一种对α阶(1<α<2)右侧Caputo分数阶导数的高阶差值逼近格式。下一步的研究可以将这种高阶差分格式应用到求解其他含有Caputo分数阶导数的差分方程并进行误差估计,除此之外,还可以构造α阶(1<α<2)Riesz-Caputo分数阶导数的高精度数值逼近格式,以更高效地解决一些时间或时空分数阶微分方程。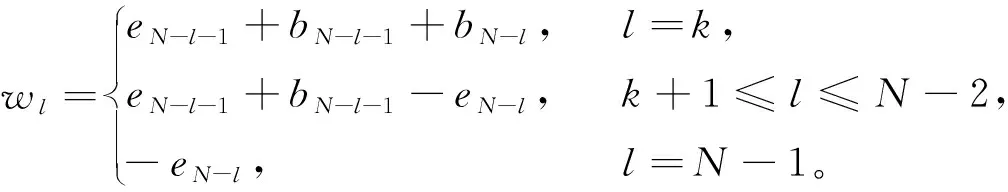
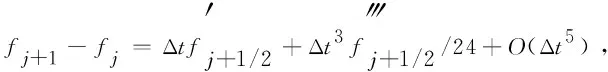
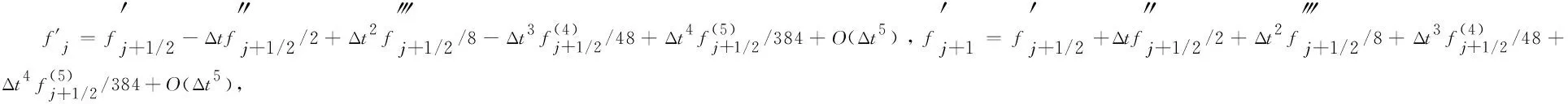
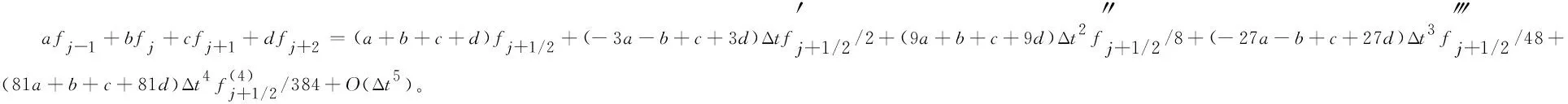
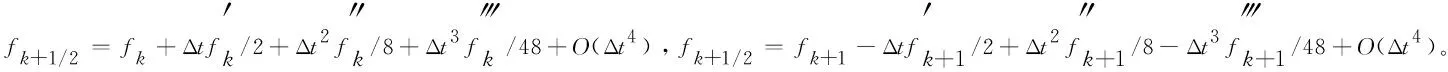
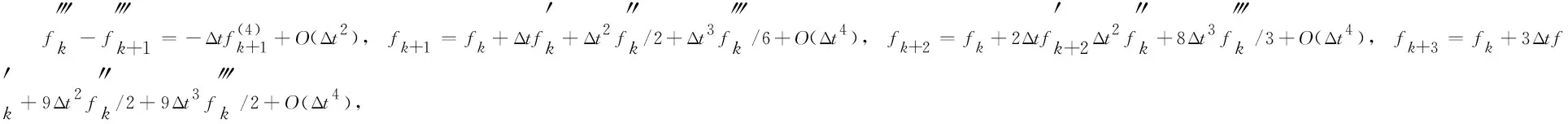
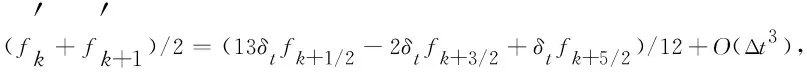
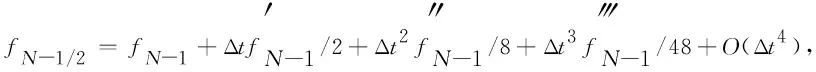
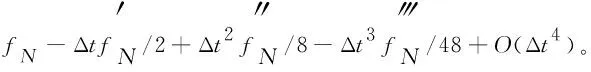
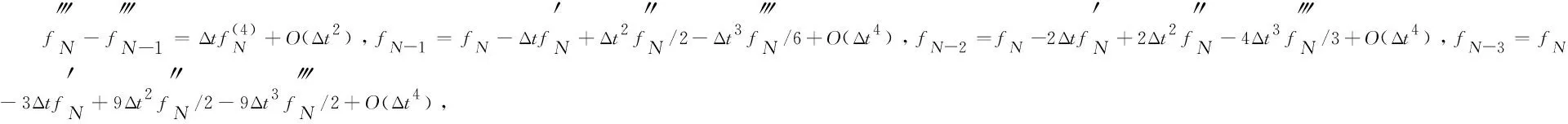
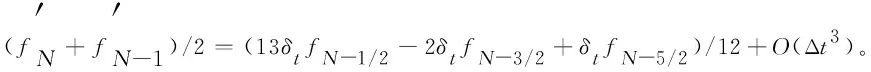
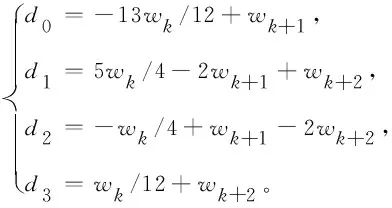
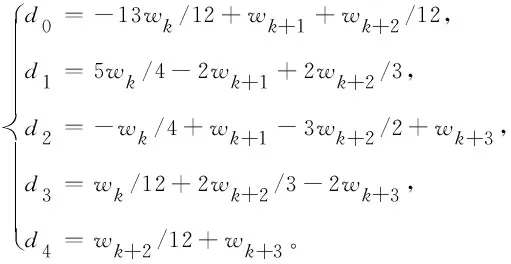
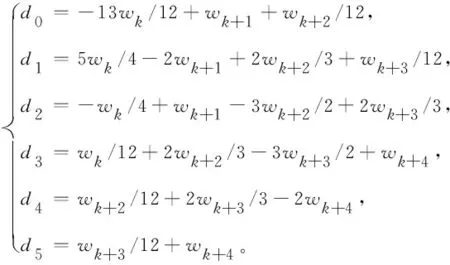
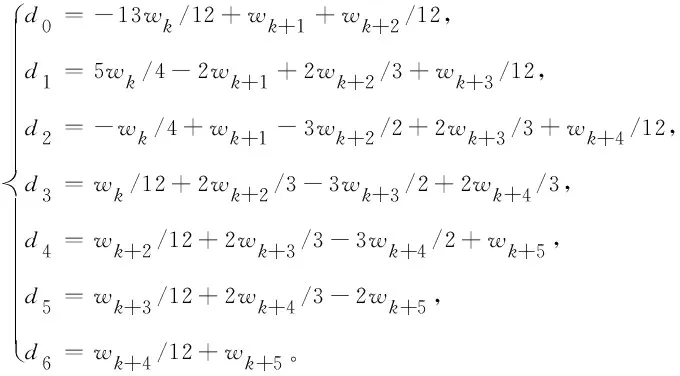
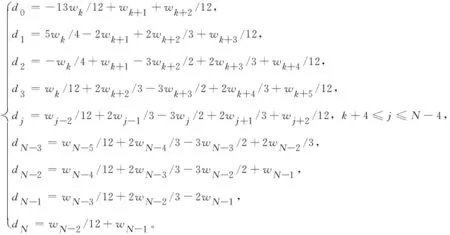
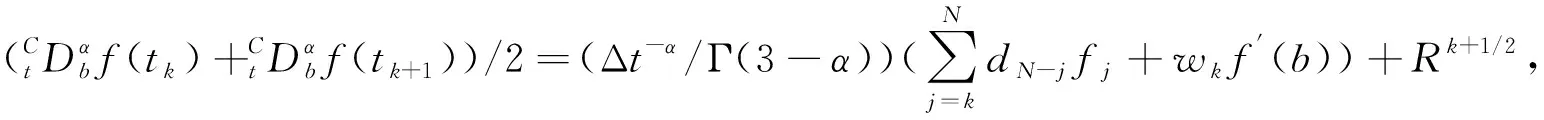
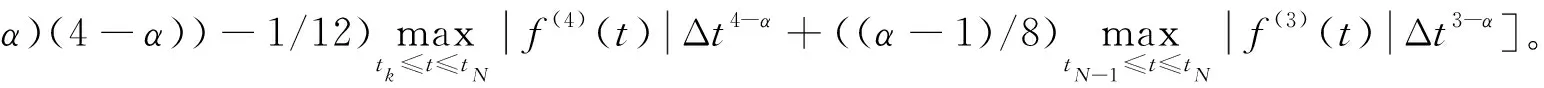
2 α阶(1<α<2)右侧Caputo分数阶导数的L2插值逼近
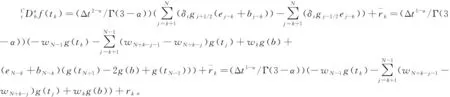
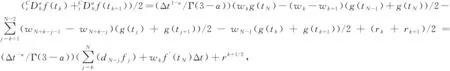
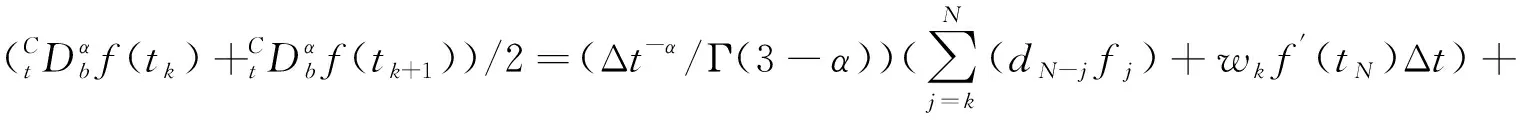
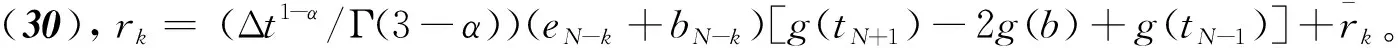
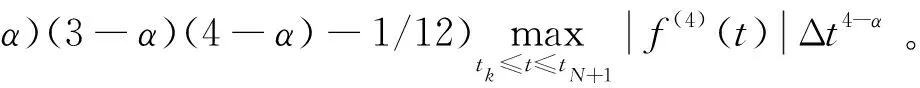
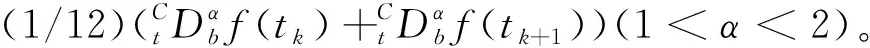

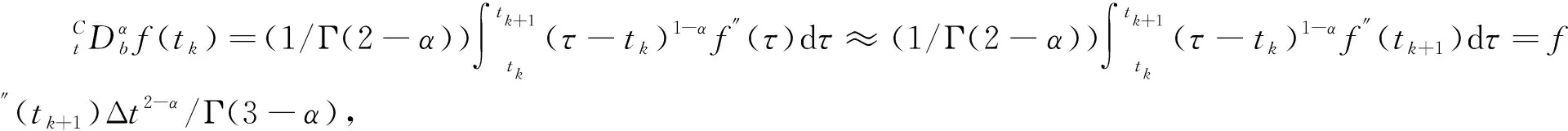
3 结论

