一类含有扰动项的Kirchhoff型方程解的多重性
2021-09-18 07:16汤碧云蓝永艺
集美大学学报(自然科学版) 2021年4期
汤碧云,蓝永艺
(集美大学理学院,福建 厦门 361021)
0 引言
考虑如下Kirchhoff型方程的Dirichlet边值问题
(1)
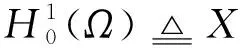
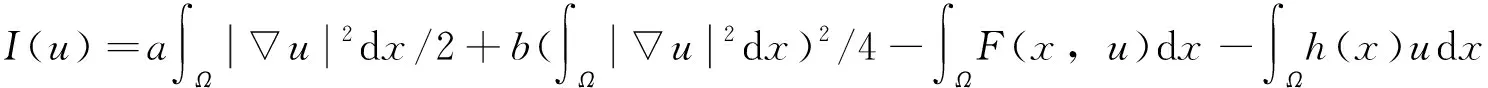
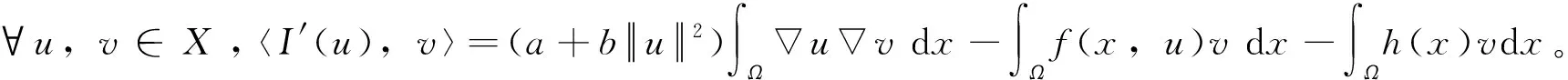
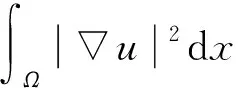
受文献[11]的启发,本文在一般的Kirchhoff 型方程中加入干扰项,形成问题(1),而且将一般的次临界条件以及AR条件弱化为条件F1)和F2),再结合Nehari流形,可以得到方程具有多重解。本文考虑一类非线性项f(x,u)具有更一般的增长性条件,假设:
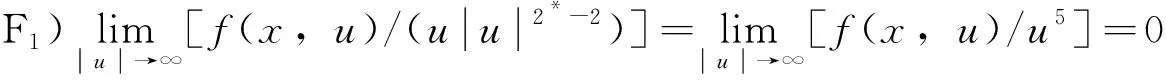
1预备知识
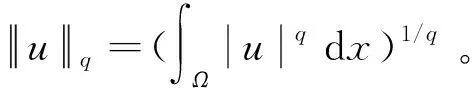
假设u≠0是I的一个临界点,即I′(u)v=0,∀v∈X,则u包含在以下集合
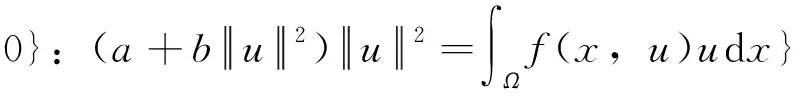
(2)
中,这个集合称为Nehari流形。由文献[9-10]知,在一定条件下,该流形微分同胚于X的单位球面。
考虑N的一个子集:
(3)
在条件F1)~F5)的假设下,给出了以下的几个引理。
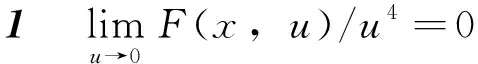
证明由F5)知,∀A>0,∃X,当u>X时,有F(x,u)≥Au4,又因为F(x,u)∈C(Ω),所以∃B>0,使得F(x,u)>-B。综上,∀u∈R,∀x∈Ω,F(x,u)≥Au4-B。
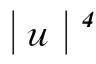
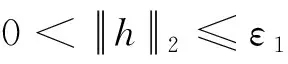
(4)
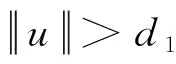
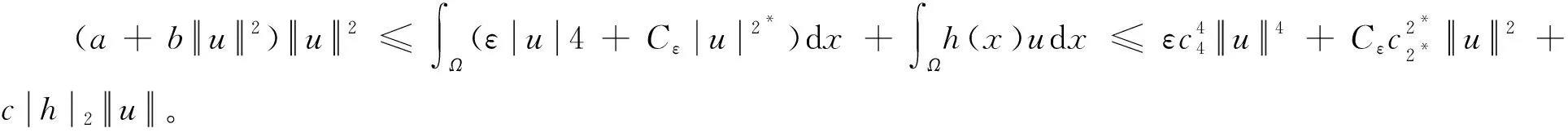
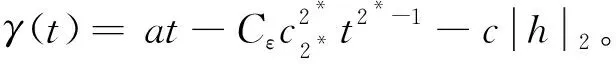
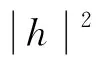
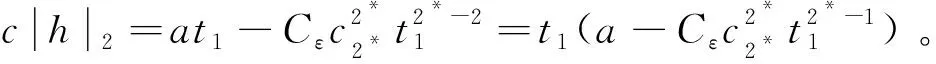
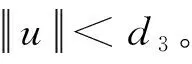
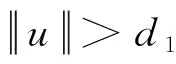
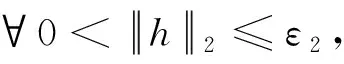
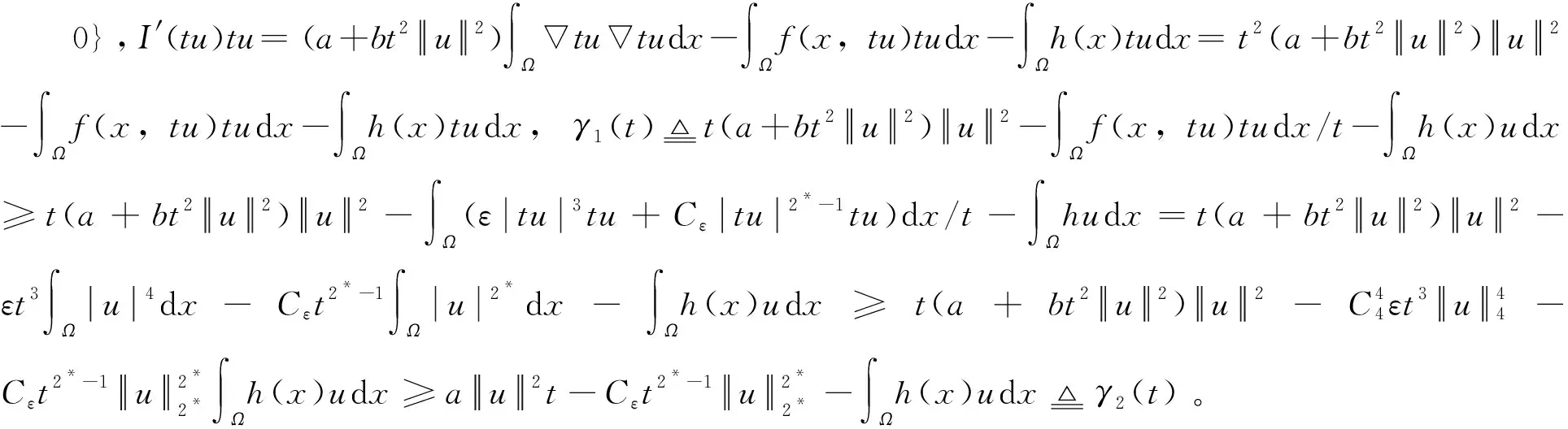
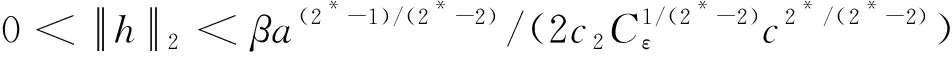
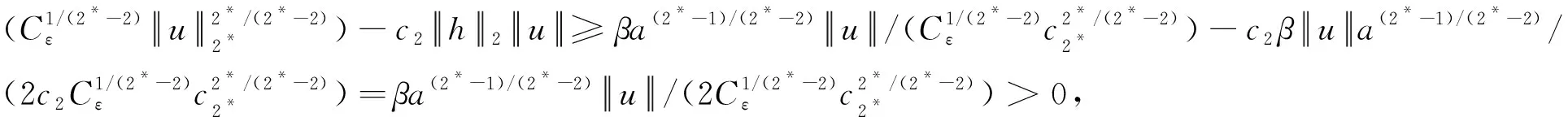
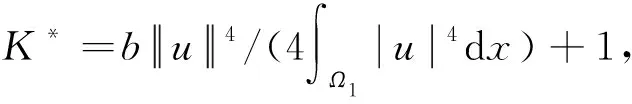
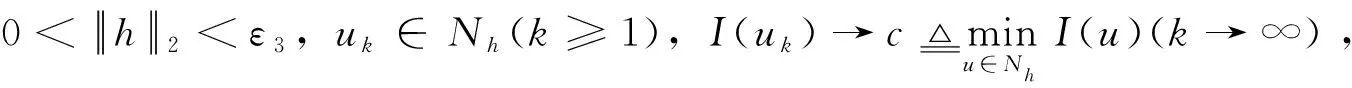
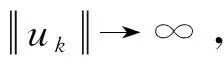
由
(5)
在式(5)中令k→∞,由Fatou引理及F(x,y)的弱连续性知,左边结果为0,右边结果为b/4,这是一个矛盾,所以{uk}有界。
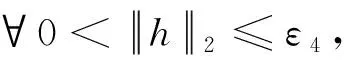
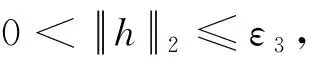
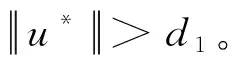
2 定理1及其证明
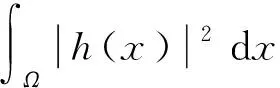
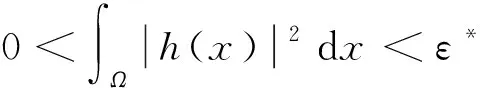
证明定理1分两步来证明。
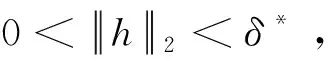
第二步:I(u)在Bτ存在局部极小值,正好是边值问题(1) 的解。
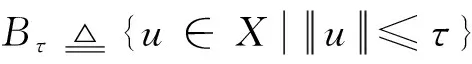
猜你喜欢
中等数学(2022年6期)2022-08-29
滨州学院学报(2022年4期)2022-08-01
中学生数理化(高中版.高考数学)(2021年11期)2021-12-21
厦门大学学报(自然科学版)(2021年1期)2021-02-02
吉林大学学报(理学版)(2021年1期)2021-01-18
华东师范大学学报(自然科学版)(2020年6期)2020-01-11
校园英语·上旬(2019年6期)2019-10-09
华东师范大学学报(自然科学版)(2019年3期)2019-06-24
科技风(2018年1期)2018-05-14
湖南师范大学学报·自然科学版(2014年3期)2014-10-24

