往复流条件下灯浮标回旋运动的参数估计
陈麒龙,毛新健
(1.集美大学理学院,福建 厦门 361021;2.交通运输部东海航海保障中心上海航标处,上海 201208)
0 引言
灯浮标的系碇结构由沉石和锚链组成。沉石起到海底固定作用,锚链长度通常按照3倍水深配置,富余的锚链起到伸缩调节和增加海底附着力的作用,但是会导致灯浮标在回旋半径内漂移[1-2]。如果灯浮标回旋半径过大,就会占用航道。因此,量化灯浮标回旋运动对航道的影响有助于优化灯浮标配布,为灯浮标位置调整提供参考数据。文献[1]用欧氏距离计算灯浮标的理论回旋半径,以灯浮标安全领域边界与航道中心线的垂直距离作为灯浮标回旋运动对航道占用的度量[1]。然而,从安装在灯浮标上的远程测控装置逐小时传回的位置数据(经度、纬度)观测到的情况是:在往复流条件下,回旋区域边界点之间的距离大于2倍理论回旋半径。说明以欧氏距离计算回旋半径误差较大,需要研究更为合理的算法。因此,本文先提出定量描述往复流条件下灯浮标回旋运动的参数,然后提出基于核密度的参数估计模型。为了度量往复流条件下灯浮标安全领域对航道的占用程度,进而优化灯浮标配布,提出基于回旋半径的航道占用率算法。
1 灯浮标回旋运动参数估计
1.1 参数设计
潮流是灯浮标回旋运动的主要外力,潮流对灯浮标的作用是持续且具有周期性的。往复流是随着涨、落潮,流向相反或基本相反的潮流,受其影响的灯浮标回旋运动所形成的区域是一个近似椭圆形的不规则区域。因此,以回旋中心和回旋半径作为往复流条件下定量描述灯浮标回旋运动的参数。
1)回旋中心参数指灯浮标回旋区域大概率的中心点;2)回旋半径参数指每日所有的灯浮标位置与回旋中心距离最大的数值,用于度量每日的灯浮标回旋区域的边界,对于近似椭圆形的回旋区域,回旋半径相当于长轴半径。
1.2 参数估计建模
1.2.1 核密度估计原理
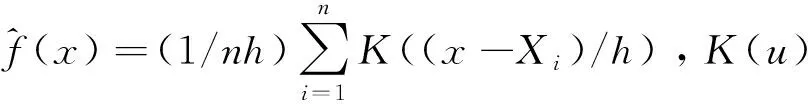
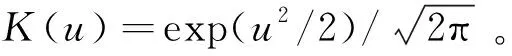
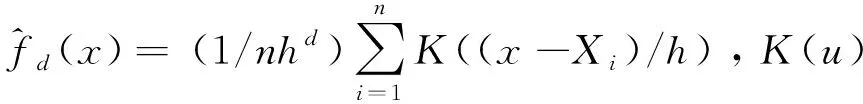
1.2.2 建模步骤
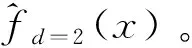
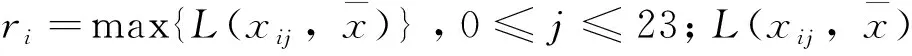
1.3 参数估计值有效性实证分析
1)实验数据来源
灯浮标的位置数据是由安装于灯浮标上的远程测控装置内的GPS模块逐小时采集并上传到航标远程测控系统。洋山港主航道的Y4#灯浮标在20191101—20191231期间的逐小时位置数据取自上海航标处的航标远程测控系统。
潮汐和潮流数据取自海洋出版社出版的《2019潮汐表》(国家海洋信息中心编),潮汐数据取与Y4#灯浮标最近的滩浒潮汐预报点的数据;潮流数据取与Y4#灯浮标最近的杭州湾口潮流预报点的数据。Y4#灯浮标所在水域的潮流属于不规则半日潮,潮流流速较大,潮流运动呈现明显的往复流;流速随涨、落潮呈周期性变化,在转流后3 h达到当日最大流速;日最大流速的变化规律与潮汐交替出现大潮日和小潮日的周期规律一致,在大潮日达到“大潮最大流速”,在小潮日达到“小潮最大流速”,大潮周期和小潮周期的平均值为14.8 d。
2)Y4#灯浮标回旋运动的参数估计
Y4#灯浮标位置的概率密度呈多峰分布如图1所示。以概率密度峰值的加权均值(E122.282 616 25°,N30.542 940 85°)作为回旋中心估计值,然后计算每日的回旋半径估计值,如图2所示。
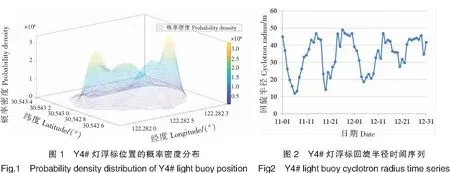
3)Y4#灯浮标回旋运动参数估计值有效性检验
Y4#灯浮标回旋运动的主要外力是往复流作用力,由n个回旋半径估计值所组成的回旋半径时间序列{rt}(1≤t≤n)应当能够反映往复流的周期性波动规律,即:{rt}呈周期性涨落,且波峰和波谷的周期在统计上应当接近14.8 d。
如表1所示,Y4#灯浮标回旋半径的波峰平均周期为14.0 d,波谷平均周期为15.0 d,波峰周期和波谷周期的平均值为14.5 d,接近14.8 d,表明回旋半径的波动周期与往复流周期具有统计上的一致性。

表1 Y4#灯浮标回旋半径时间序列波动周期Tab.1 Fluctuation cycle of Y4# lightbuoy cyclotron radius time series波Wave日期Date周期Cycle/d平均周期Average Cycle/d波峰Peak11-16 11-291312-16 1712-281214.0波谷Valley11-05-11-20 1512-051512-201515.0
4)Y4#灯浮的回旋半径波动规律分析
根据中心极限定理,当样本量大于30时,回旋半径样本均值经过标准化后应当近似服从标准正态分布。检验方法是:对连续61 d的回旋半径估计值进行49次简单随机抽样,每次抽样的样本容量为40,将49个样本均值标准化后使用Kolmogorov-Smirnov检验法来检验是否服从标准正态分布,检验原理如下。
原假设:回旋半径样本均值服从正态分布;
备择假设:回旋半径样本均值不服从正态分布;
统计量D=|Fn(x(i))-F0(x(i))|max,1≤i≤n。其中:F0(x)是正态分布函数;Fn(x)表示一组随机样本的累积概率函数;D表示F0(x)与Fn(x)差距的最大值;取显著性水平α=0.05,用p-value表示实际观测的显著性水平,当实际观测值D 当显著性水平α=0.05时,49个样本均值的Kolmogorov-Smirnov检验的统计量D=0.060 852,p-value=0.988 4,p-value>α,不拒绝原假设(回旋半径样本均值服从正态分布)。 图3中叉号位置的数值为48.21 m,是回旋半径总体均值的点估计,回旋半径数值的波动规律是:沿着48.21 m作周期性波动,交替出现波峰和波谷。 5)实验结论 以Y4#灯浮标为例证明了灯浮标回旋半径的波动周期与往复流周期具有统计上的一致性,基于核密度的回旋中心和回旋半径参数估计值能够有效反映灯浮标回旋运动规律。Y4#灯浮标回旋半径的总体均值点估计和Kolmogorov-Smirnov检验,证明了Y4#灯浮标回旋半径的波动规律是:沿着回旋半径的总体均值作周期性波动,交替出现波峰和波谷。 灯浮标安全领域是指船舶为了避碰,在灯浮标的回旋区域之外保持足够的避碰距离所形成的区域。在灯浮标安全领域之外行驶的船舶不会碰撞灯浮标,在灯浮标安全领域之内行驶的船舶由于避碰距离不足,有可能碰撞灯浮标。灯浮标安全领域对航道的占用程度可以衡量灯浮标回旋运动对航道的影响。灯浮标回旋半径可以用于推算灯浮标安全领域对航道的占用率,有助于分析和优化灯浮标配布。 (1) 在墨卡托投影坐标系中,航道边界线与灯浮标安全领域的交点为A(x1,y1)和B(x2,y2),如图4所示。航道边界线斜率k的计算公式: k=(y2-y1)/(x2-x1)。 (2) 以A和B为端点形成的线段称为弦长AB,计算公式: (3) 灯浮标的回旋中心点O与弦长AB之间的垂线与AB相交于点E,以点O和点E为端点形成的线段称为弦心距OE,计算公式: (4) 线段OA、OB和弦长AB所形成的三角形称为弦心三角形,其面积计算公式为: (5) SOAB=πR2arcsin(AB/2R)/180。 (6) 用阴影部分表示的灯浮标安全领域与单侧航道相交的区域,其面积计算公式为: (7) 航道宽度为W,单侧航道的宽度为W/2,单侧航道在灯浮标附近区域的面积计算公式为: So=W×AB/2。 (8) 灯浮标安全领域对航道的占用率用Z表示,Z越大表示灯浮标安全领域与航道的重叠区域越大,计算公式: (9) 1)Y4#灯浮标安全领域对航道的占用率计算 以Y4#灯浮标为例,回旋半径的概率密度分布如图5所示,当回旋半径到达72.41 m时,累积概率为1。所以,取72.41 m作为Y4#灯浮标最大回旋半径的估计值。船舶与灯浮标必须保持至少40 m的避碰距离,因此Y4#灯浮标安全领域半径R=112.41 m。 已知洋山港主航道在Y4#灯浮标附近区域的宽度W=800 m,在墨卡托投影坐标系中,航道边界与安全领域的两个交点坐标分别是:A(13 612 332.73,3 573 562.28)和B(13 612 548.31,3 573 527.86),根据以上公式计算得到航道占用率Z=0.16。 2)分析与建议 Y4#灯浮标附近航道边界水域的水深为19.3 m,水深条件较好,常有船舶在航道边界附近行驶。在20191101—20191231期间,经过Y4#灯浮标所在的单侧航道的船舶共计1 249艘次,其中有274艘次从Y4#灯浮标安全领域内经过。Y4#灯浮标安全领域对航道的占用率达0.16,途经的船舶中有21.9%的船舶与Y4#灯浮标之间的避碰距离不足40 m。建议将Y4#灯浮标沿垂直航道边界线向外移动113 m,确保航道边界附近行驶的船舶与Y4#灯浮标之间有足够的避碰距离。 为了分析往复流条件下的灯浮标回旋运动规律,先提出以回旋中心和回旋半径作为定量描述灯浮标回旋运动的参数,然后提出基于核密度的参数估计模型,并以洋山港主航道Y4#灯浮标为例,证明了参数估计值能够反映灯浮标回旋运动规律。为了定量描述往复流条件下灯浮标安全领域对航道的占用程度,进而优化灯浮标配布,提出基于回旋半径的航道占用率算法,以洋山港主航道Y4#灯浮标为例,证明了此算法能够有效度量灯浮标安全领域对航道的占用程度,然后结合途经灯浮标的船舶统计数据,分析灯浮标回旋运动对航道和船舶的影响,最后提出调整灯浮标配布的建议。下一步将继续研究回转流水域、非典型潮汐潮流水域的灯浮标回旋运动规律和参数估计模型。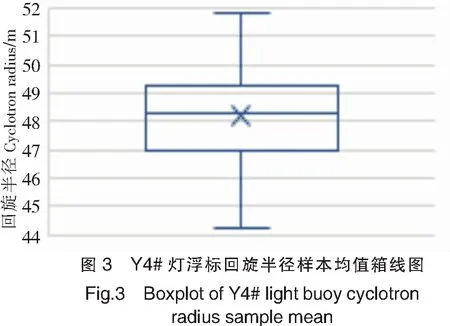
2 灯浮标安全领域占用航道的定量分析
2.1 占用率算法
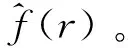


2.2 实例分析

3 结论

