带旋转与尺度估计的全卷积孪生网络目标跟踪算法

姬张建，任兴旺

（1.山西大学计算机与信息技术学院，太原 030006；2.山西大学大数据科学与产业研究院，太原 030006）

（*通信作者电子邮箱jizhangjian@sxu.edu.cn）

0 引言

目标跟踪是计算机视觉领域中一个重要的研究课题，在机器人运动路径规划、汽车辅助驾驶以及军事目标追踪等方面有着广泛的应用，进而得到了越来越多专家学者的关注［1-2］；但是在真实场景中面临的各种挑战，如复杂的背景、光照变化、目标物被遮挡以及运动物体的旋转尺度变化等，严重影响现有目标跟踪算法的性能，使得如何准确地对目标进行跟踪成为研究难题。

目前常见的目标跟踪算法可分为两类：基于相关滤波框架的跟踪算法和基于深度孪生网络框架的跟踪算法。相关滤波算法主要应用于信号处理领域，用来描述两个信号之间的相关性，目标跟踪的过程同样可视为模板与待搜索区域间相关性的计算。Bolme 等［3］首次将相关滤波思想引入到目标跟踪任务中，提出了基于平方误差最小和滤波器的跟踪算法，实现了每秒600 多帧的跟踪速度，但跟踪性能较差。之后为了提高算法的鲁棒性，文献［4］将表征能力更强的梯度直方图（Histogram of Oriented Gradients，HOG）特征［5］引入到相关滤波跟踪模型中实现了更好跟踪性能的核相关滤波（Kernelized Correlation Filters，KCF）算法；然而，该算法仅限于估计目标的平移运动，当目标发生较大的尺度变化时跟踪性能很差。Danelljan 等［6］将深度特征引入跟踪模型中，提出了一种高效的卷积操作（Efficient Convolution Operators for tracking，ECO）算法。由于相关滤波本身缺少对尺度变化的估计能力，文献［7］使用可分离的尺度滤波器来估计目标的尺度提出带尺度估计的算法DSST（Discriminative Scale Space Tracker）。文献［8］则采用多尺度搜索策略SAMF（Scale Adaptive with Multiple Features tracker）解决了传统的相关滤波跟踪器不能解决被跟踪目标尺度变化的问题。为了解决现有的目标跟踪器不能适应运动目标旋转的问题，Li 等［9］在相关滤波跟踪模型下引入对数极坐标系下的谱相关算法用于旋转估计，虽然该算法对旋转目标的跟踪有一定的适应性，但由于其结果是谱相关与相关滤波模型联合训练实现，故对其他如孪生网络等跟踪模型不具备良好的迁移性。另一种主流目标跟踪算法是基于深度孪生网络框架的模型，该结构最早由Chopra 等［10］用来比较两组数据之间的相似性。而Bertinetto 等［11］则开创了将孪生网络应用到目标跟踪的先河，提出利用全卷积孪生网络（Fully-Convolutional Siamese networks，SiamFC）计算模板与搜索区域之间的相似度实现目标的跟踪，取得了较好的性能；但SiamFC 算法没有用回归去调整候选框的位置，且需要多尺度测试来估计跟踪框的大小，破坏了模型的优雅性。为了解决这个问题，Li 等［12］在孪生网络的基础上引入了区域建议网络［13］，提出了区域建议孪生网络（Siamese Region Proposal Network，SiamRPN）模型，能更好地适应被跟踪目标的尺度变化；但没能解决具有旋转变化的目标跟踪问题。Wang 等［14］提出的SiamMask 算法则将目标分割子任务引入到孪生网络结构中，在实现目标跟踪的同时进行目标分割。

为了解决现有基于孪生网络的跟踪算法不能准确地跟踪具有旋转变化的目标问题，本文提出一种带旋转与尺度估计的SiamFC 跟踪算法。在SiamFC 算法跟踪定位基础上，将目标搜索区域从笛卡儿坐标系转换到对数极坐标系下，利用核相关滤波器估计平移量，进而获得目标的旋转角度和尺度，并对SiamFC 的初始跟踪结果的目标位置和区域进行修正得到最终的跟踪结果，极大地提高了SiamFC 跟踪模型的准确率和成功率。

1 相关理论

目标跟踪任务实现的过程可视为：根据待跟踪视频序列所给定初始帧中目标状态，预测后续帧中该目标的区域位置信息。SiamFC 算法首次将孪生网络模型应用于单目标跟踪任务中，通过利用大量数据训练获得的孪生网络来提取模板与搜索区域的深度特征，计算二者之间的相似度实现跟踪；但是当被跟踪目标发生尺度或旋转变化时，SiamFC 算法的跟踪结果不能精确地拟合目标区域。因此，本文在全卷积孪生网络基础上引入了尺度与角度估计模块来提升算法性能。

1.1 SiamFC跟踪模型

SiamFC 算法作为基于孪生网络跟踪模型的典型代表，实现过程可分为训练与跟踪两个阶段。该算法的结构示意图如图1所示。

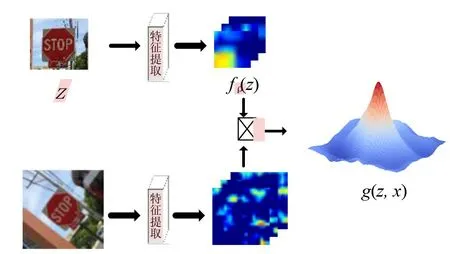
图1 SiamFC算法结构示意图Fig.1 Schematic diagram of SiamFC algorithm architecture

图1中：z表示从初始帧抠出的目标模板，x为表示从后续帧抠出的包含目标的待搜索区域。特征提取网络采用卷积神经网络（Convolutional Neural Network，CNN）［15］作为骨架网络，去掉原始的池化层和全连接层，引入批归一化（Batch Normalization，BN），得到全卷积网络结构。

孪生网络以图像对(z，x)作为输入，利用卷积神经网络fρ(⋅)提取相应的特征图，则得分图可表示为：

其中：⊗表示卷积操作；b表示偏置向量。对于目标跟踪而言，得分图的最大值位置即为目标在当前帧中的位置。

为了实现这个目的，首先需要从训练视频中搜集大量的图像样本对(zi，xi)离线训练网络模型，每一个样本对都有一个真实的空间标签图Yi∈{1，-1}，在空间标签图中，真实的目标位置为正类，其他所有位置都是负类。为了训练模型，需要在整个训练集上利用随机梯度下降算法最小化元素级的Logistic损失L(⋅)，相应的优化目标函数为：

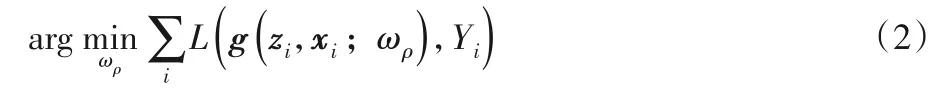
其中：ωρ表示学习的孪生网络模型参数。

在目标跟踪阶段，以前一帧的目标位置为中心抠出搜索图像，利用训练好的网络模型fρ(⋅)提取搜索图像的特征图，通过式（1）计算得分图g(⋅)。为了得到更精确的目标位置，需要利用式（3）对得分图进行双三次插值得到上采样的结果：

其中：p为插值后的点；pij分别表示p点周围16个点的坐标；βij表示插值参数。经插值变换后得分图的最大值所处的位置作为目标位置。

1.2 相关滤波算法模型

在传统的相关滤波模型中，每一个训练样本z由从初始图像帧抠出的图像区域I∈RM×N提取的d维特征图构成。在每 一个空间位置(m，n) ∈Ω：={0，1，…，M-1}×{0，1，…，N-1}，都有一个d维的特征向量z(m，n) ∈Rd。对于训练样本z的每一个位置z(m，n) ∈Rd，都有一个期望的输出值y(m，n)。那么，可通过最小化下面的损失函数（4）得到关于训练样本z∈RM×N×d对应的每一层滤波器wl（l∈{1，2，…，d}）：

其中：⊗表示循环卷积操作；λ≥0为正则化参数。式（4）是一个线性岭回归问题，为了求解它，采用帕萨瓦尔公式，它能被转换到傅里叶域上并获得下面形式的封闭解：

其中：Zl、Y分别表示zl、y的离散傅里叶变换；分别表示wl、zl的离散傅里叶变换的复共轭。

在目标跟踪阶段，当获得了每一层的滤波器wl后，以xl∈RM×N表示从当前帧中的目标搜索图像区域提取的第l∈{1，2，…，d}层的特征图，那么相应的得分图可通过式（6）计算得到：

其中：Xl表示xl的离散傅里叶变换；F-1(⋅)表示离散傅里叶变换的逆变换。得分图g的最大值所处的位置即为待跟踪目标在当前帧中的位置，这一滤波实现过程如图2所示。

图2 相关滤波示意图Fig.2 Schematic diagram of correlation filtering

1.3 对数极坐标变换下的尺度和旋转估计

对数极坐标图像的应用，来源于对生物视网膜生理结构所获得的灵感，作为一种尺度与旋转估计的算法常被应用于图像处理领域［16］。图3展示了图像在笛卡儿坐标系和对数极坐标系之间变换的基本原理，左图中的圆环线与直线分别对应右图中的竖线与横线。

图3 对数极坐标变换示意图Fig.3 Schematic diagram of log-polar transformation

图3左图中的笛卡儿坐标系定义为：

其中：i 表示复数的虚单位。以中心点(u0，v0)为原点，将笛卡儿坐标系任意一点坐标(u，v)，变换到对数极下的坐标(s，θ)的表达式为：

若将图像I(u0，v0)以(u0，v0)为原点旋转Δθ，同时尺度变化Δs，那么变化后的图像在对数极坐标系下可表示为：

其中：I′表示对数极坐标系下的图像；(s，θ)和(s′，θ′)分别表示变化前后图像I(u，v)在对数极坐标系下的坐标。由此可知，图像在笛卡儿坐标系下的旋转和尺度变化等价于对数极坐标系下的平移变化。

基于这一性质，可以在对数极坐标系下利用相关滤波估计被跟踪目标的旋转和尺度变化。若zlp表示训练样本z在对数极坐标系下的特征图，那么根据式（11）可得到对数极坐标系下傅里叶域上的每层滤波器，即：

进而可通过得分图glp最大值所处的位置相对于中心位置的偏移量估计被跟踪目标的尺度和旋转变化。若在当前帧横坐标的偏移量为Δs，纵坐标的偏移量为Δθ，那么在当前帧目标的尺度大小和旋转角度可表示为：

其中：α、θ表示目标在前一帧中尺度大小和旋转角度；α′、θ′表示在当前帧中目标的尺度大小和旋转角度。此外，为了适应目标的变化，本文采用线性加权的方式更新对数极坐标系下每层傅里叶滤波器

2 算法描述

本文的算法包含位置估计模块和尺度与角度估计模块，总体的算法流程如图4 所示。本文算法的具体实现步骤如下：

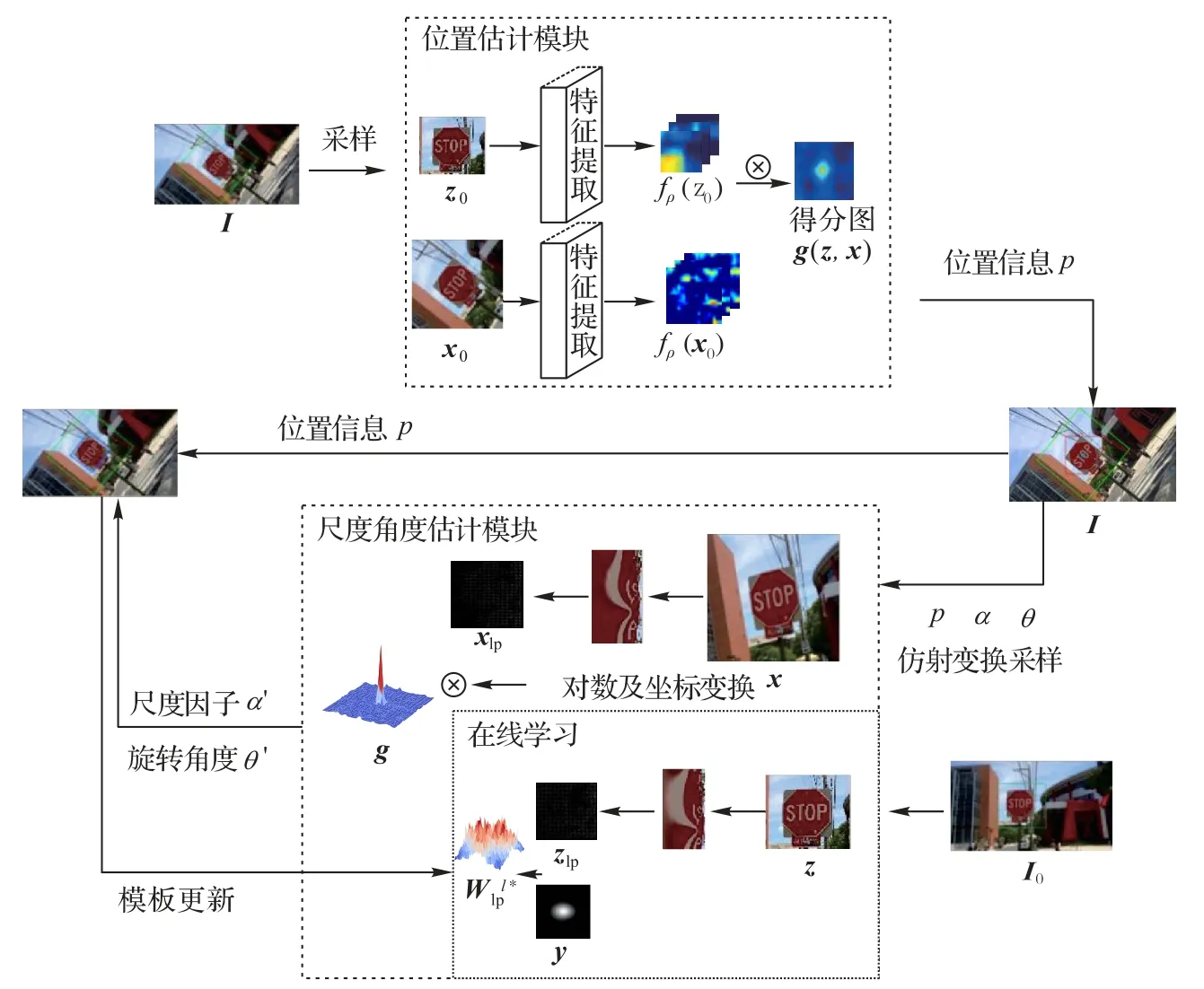
图4 带旋转与尺度估计的SiamFC算法的总体流程Fig.4 Overall flowchart of SiamFC algorithm with rotation and scale estimation

步骤1 在初始帧I0中，根据给定的目标位置p0、目标的大小以及目标初始的尺度因子α和初始旋转角度θ，利用仿射变换抠出目标模板图像z，并将其转换到对数极坐标系下提取特征图zlp，计算对数极坐标系下的傅里叶域上的每层滤波器

步骤2 在当前帧I中抠出待搜索图像区域x0和目标模板图像z0输入SiamFC 模型中，得到得分图，并根据相应得分图最大值所处的位置估计目标在当前帧中的位置p。

步骤3 在当前帧I中，根据目标位置p和给定的目标大小和目标初始尺度因子α和初始旋转角度θ，利用仿射变换抠出目标的待检测图像区域x，将其转换到对数极坐标下提取特征图xlp，利用相关滤波算法得到得分图，并估计出横纵坐标的偏移量Δs和Δθ，利用式（13）～（14）估计出目标在当前帧中的尺度因子α′和旋转角度θ′。

步骤4 根据当前帧的目标位置p、尺度因子α′和旋转角度θ′更新先前的相关参数，并基于更新后的参数在当前帧抠出新的目标模板图像，转换到对数极坐标系提取相关特征图，更新滤波器。

步骤5 返回执行步骤2，直至序列结束。

3 实验与分析

实验运行环境：内存为8 GB，CPU 为Intel 酷睿i7 处理器，主频为3.6 GHz。

特征表示：在本文的相关滤波模型中，使用31 维的HOG特征，该特征采用的元胞大小为4 × 4。

实验数据集：选取了两个目标跟踪数据集POT（Planar Object Tracking in the wild）和OTB2015（Visual Tracker Benchmark 2015）。其中POT数据集包含30组视频序列，涵盖了尺度变化（Scale Change，SC）、目标旋转（Rotation，RT）等目标跟踪任务中常见的7种挑战；OTB2015数据集包含100组真实跟踪场景中可遇到的目标尺度变化、遮挡、运动模糊以及快速运动等情形的视频序列。

3.1 评价指标

目标跟踪通常采用精确率与成功率来评价跟踪算法的性能，本文沿用POT 数据集中的对准误差eAL（ALignment error）作为精度评价指标，选择单应性差异S（Homography discrepancy）作为准确率评价指标［17］，表达式分别如下：

3.2 实验结果

3.2.1 POT数据集实验结果

本文选取了ECO-HC、SiamFC、SAMF、DSST、KCF 和SiamMask 与本文提出的算法模型在POT 数据集上进行了对比实验。其中，ECO-HC为ECO算法未使用深度特征的版本。

表1 展示了每个算法在目标旋转、尺度变化和综合因素挑战下的跟踪成功率与准确率的比较结果，以及各个算法在POT 数据集上的平均帧率；表2 展示了本文提出的算法与原始SiamFC 算法在POT 数据集上7 种不同挑战情形的实验结果。图5（a）给出了不同算法在POT 数据集所有序列上获得的准确率和成功率曲线；图5（b）显示了在POT 数据集中只包含目标旋转序列的跟踪结果；图5（c）为在POT 数据集上仅包含尺度变化序列的跟踪结果，其中准确率性能以对准误差阈值tp=20 时的准确率大小排名，成功率按单应性阈值ts=10时的成功率值的大小进行排名。

图5 多种算法在POT数据集成功率与准确率曲线Fig.5 Curves of success rate and accuracy of several algorithms on POT dataset

从表1 可以看出，本文提出的算法在POT 数据集上跟踪成功率与准确率分别达到了51.8%和53.3%，尤其在含有旋转的序列上跟踪成功率与准确率更是达到了75.9%和85.9%，明显优于其他几种跟踪算法。虽然在尺度序列上的性能不及ECO-HC 和DSST（主要原因在于这两种算法采用了多尺度特征融合，对尺度变化采样更精细），但本文算法不需要在很多尺度上进行特征提取，故对尺度的估计效率也更高。以V02-2 为例，本文算法估计每帧目标尺度的时间开销仅为0.75 ms，而ECO-HC 用时约为1.5 ms。从表3 可以看出，本文算法的帧率为3.271 frame/s，相较于SiamFC算法虽略有下降，但精度却得到了较大的提升；效率不及其他算法的原因在于只有本文的模型与SiamFC 算法使用了深度神经网络，但是为保证对比实验的公平性，所有实验均在CPU 环境下进行，而CPU极大地限制了基于深度神经网络模型性能的发挥。

表1 多种算法在POT数据集上的成功率和准确率比较Tab.1 Comparison of success rate and accuracy of several algorithms on POT dataset

表2 改进前后的SiamFC算法在POT数据集上7种挑战下的成功率与准确率Tab.2 Comparison of success rate and accuracy of SiamFC algorithms before and after optimization in 7 challenges on POT dataset

表3 多种算法在POT数据集上的帧率比较Tab.3 Comparison of frame rate of several algorithms on POT dataset

从表2 结果可知本文算法在多个挑战因素上均优于SiamFC 算法的结果，在综合挑战序列中成功率与准确率提升了13.5 个百分点和13.4 个百分点；尤其在旋转序列上，性能显著优于SiamFC 算法，充分验证了本文算法在估计目标旋转方面的有效性。鉴于SiamMask 算法是采用分割掩模获得带旋转的矩形跟踪框，无法提供帧间连续的角度变化信息，不能采用POT数据集上所提出的评价指标比较它和本文提出的算法的性能，故而采用目标跟踪任务中常用的评估指标（中心点误差和交并比）比较两者的性能，相关阈值参数分别设定为20和0.5，实验结果如表4。

表4 本文算法与SiamMask算法成功率与准确率对比结果Tab.4 Comparison result of success rate and accuracy of the proposed algorithm and SiamMask algorithm

由表4 结果可以看出，在POT 全部数据集上，本文提出的算法与SiamMask算法相比，在成功率上仅低2个百分点，而在精度上却高5 个百分点。特别是对于包含尺度和旋转变化的序列，本文算法在成功率和精度上都明显优于SiamMask。此外，SiamMask 中引入的像素分割模块会严重降低该算法的效率，而本文提出的算法采用对数极坐标系下的相关滤波模型估计尺度和角度变化，基本不会增加额外的计算开销。

3.2.2 OTB2015数据集实验结果

在OTB2015 数据集上，选取ECO-HC、DSST、SiamFC、KCF和Struck（Structured output tracking with kernels）［18］共5种相关的跟踪算法与本文算法进行比较，准确率曲线与成功率曲线如图6所示。从图6中所展示的实验结果可以看出，本文提出的算法性能仅次于ECO-HC 算法，优于SiamFC 和其他几种跟踪算法。但与SiamFC 算法相比，本文提出的算法在OTB2015数据集上的性能提升不及POT 数据集上那么显著，主要原因在于OTB 数据集上采用平行于坐标轴的矩形框作为理想的跟踪框，而由此产生的标定误差会严重影响算法的性能。

图6 OTB2015数据集上的成功率与准确率曲线Fig.6 Curves of success rate and accuracy of several algorithms on OTB dataset

3.3 实验结果可视化表示

表5 给出了POT 中V09_2 序列部分帧关于目标位置、尺度和旋转角度的跟踪估计结果与相应的真实值比较结果，其中位置用目标中心点的坐标表示，尺度与角度以第一帧为基准来比较，且以逆时针旋转为负。在图7中，根据OTB2015数据集中Crossing 和Crowds 序列的跟踪结果绘制相应的目标运动轨迹图。此外，本文也在POT 和OTB2015 两个数据集上定性比较了KCF、SiamFC 及本文算法的性能。从图8 给出的结果可以看出，本文提出的算法在包含尺度变化和旋转变化的序列上得到的跟踪框更精确。

表5 VO9_2序列的部分帧中目标位置、尺度与旋转角度Tab.5 Object positions，scales and rotation angles in some frames of V09_2 sequence

图7 目标的跟踪轨迹图Fig.7 Tracking trajectory of object

图8 三种跟踪方法在部分数据上的可视化结果Fig.8 Visualization results of three tracking methods on some data

4 结语

本文针对SiamFC 模型在目标存在旋转和尺度变化的情况下跟踪不精确的问题，提出以SiamFC 模型得到目标的位置为基础，将待搜索的图像区域转换到对数极坐标下，利用相关滤波模型估计目标的尺度和旋转角度，构建了一个能同步估计被跟踪目标的位置、尺度和旋转角度的目标跟踪模型。与SiamFC 算法相比，该算法在跟踪成功率与准确率上都有较大的提升，但仍有进一步提升的空间，下一步我们打算从以下两个方面着手提升算法的性能：1）因本文提出的旋转、尺度估计模型具有很好的移植性，可将其与性能更好的孪生网络跟踪模型相结合来提升算法的整体性能；2）本文所提出的旋转、尺度估计模型与孪生网络定位模型相独立，而且仅选取了HOG特征用于旋转与尺度的估计，我们拟将其与定位模块统一训练，利用深度学习网络构建统一的位置、尺度与旋转角度同步估计的孪生网络，以获得更好的跟踪结果。