面向C‑V2X通信的基于深度学习的联合信道估计与均衡算法

陈成瑞，孙 宁，何世彪，廖 勇*

（1.重庆工程学院电子信息学院，重庆 400056；2.重庆大学微电子与通信工程学院，重庆 400044）

（*通信作者电子邮箱liaoy@cqu.edu.cn）

0 引言

我国是全球最大的汽车生产国和销量国，且汽车行业正处在向新能源、智能网联和自动驾驶等转型升级的关键机遇期，在未来的场景应用中，车联网（Vehicle to Everything，V2X）通信将是最重要的场景之一［1］。并且，随着智能化的潮流兴起，智能交通系统愈加受到人们的关注，而V2X 作为下一代智能交通的核心，其相关技术的研究也会推动智能交通系统的发展。V2X 是指通过装载在车辆上的传感设备、车载终端及电子标签来提供车辆数据信息，利用先进的通信技术获取到车辆周围的环境信息，进而对车辆进行管控和提供服务［2］。具体来说，V2X 包括的通信场景主要有车辆间通信（Vehicle to Vehicle，V2V）、车辆与路边基础设施通信（Vehicle to Infrastructure，V2I）、车辆与行人通信（Vehicle to Person，V2P）和车辆与网络通信（Vehicle to Network，V2N）等［3］。

为了支持V2X 的在实际生活中的应用，已有相关组织提出了V2X 通信技术标准，主要有短程通信（Dedicated Short Range Communication，DSRC）［4］技术和基于蜂窝网络的车联网（Cellular-Vehicle to Everything，C-V2X）［5］技术，其中C-V2X包括LTE-V2X 技术和5G NR-V2X 技术。LTE-V2X 作为面向车路协同的通信综合解决方案，能够在高速移动环境中提供低时延、高可靠、高速率的通信能力，满足车联网多种应用的需求。本文聚焦于LTE-V2X 通信技术标准，对其接收机中的信道估计与均衡技术进行联合考虑，以改善通信系统的性能。

作为无线通信系统接收机的关键部分，信道估计与信道均衡性能的好坏将直接影响到整个通信系统的通信质量。信道估计利用导频符号获取部分频点或时刻的信道冲激响应，并结合信道插值方法计算整个时频域资源块上的信道响应，最后利用估计得到的信道响应进行信道均衡，来消除在无线信号传播过程中由信道引入的信号畸变和干扰。由上述分析可以得知，信道均衡需要以信道估计的结果作为输入，以恢复原始的发送信号，而在信道估计环节如果不能精准地获得信道状态信息（Channel State Information，CSI），将会对后续的信道均衡环节的系能产生较大影响。而信道估计的算法设计很大程度上取决于该算法应用场景下的信道特征，在C-V2X 通信场景中，由于终端处在高速移动的状态下，因此在多径效应和多普勒效应的联合作用下信道将会呈现出时频域选择性衰落，即双选衰落；此外，由于接收天线阵列与基站之间的波束的几何参数存在快速时变的特性，导致信道冲激响应的时域自相关系数呈现出时变的特性，即非平稳特性。由于在高速环境下信道表现出上述的两种特性，大幅增加了获取到精确CSI 的难度，一旦在信道估计环节引入过大的误差，那么均衡器就无法利用CSI 来对接收数据进行恢复，无疑会导致通信系统的可靠性降低。

C-V2X 通信接收机各项处理技术的目的都是为了更加高效且精准地从接收数据中检测出发送数据，因此在本文中，不仅考虑信道估计与信道均衡技术中的单独环节，还对两者进行联合考虑，将其视为一个整体。深度学习是一种数据驱动的方法，它可以从大量的数据中学习到隐含在数据中的规律，而这也恰恰与本文的目标相吻合，即从接收数据中直接检测出原始的发送数据，不进行显式的信道估计。为了方便描述，将本文中所提出的面向车联网C-V2X环境中的基于深度学习的联合信道估计与均衡算法称为V-EstEqNet。

1 相关工作

为了获取更加准确且实时的CSI，许多研究人员都致力于信道估计的研究。文献［6］提出了一种基于基扩展模型（Basis Expansion Model，BEM）的贝叶斯滤波的信道估计方法，降低了估计复杂度的同时保证了系统性能；文献［7］采用了导频与数据叠加的帧结构，提出了一种改进的迭代卡尔曼滤波（iterative Extend-Kalman Filter，iEKF）信道估计算法；文献［8］对水声正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）通信系统中的信道估计进行了研究，提出了一种基于压缩感知的稀疏信道估计算法。大量的信道估计研究都表明，如果可以准确地获取到CSI，会在一定程度上提升通信系统的误码率（Bit Error Rate，BER）性能，但是，信道估计根据其算法复杂度的不同，需要在不同程度上占用系统资源，也在一定程度上也增加了通信系统的功耗。

信道均衡技术是指为了提高衰落信道中的通信系统的传输性能而采取的一种抗衰落措施。常用的均衡算法主要分成线性均衡算法和非线性均衡算法［9］，线性均衡算法主要有迫零（Zero Forcing，ZF）均衡算法和最小均方误差（Minimum Mean Square Error，MMSE）均衡算法等。ZF 均衡算法较为简单，只是在信道估计结果的基础上通过简单的矩阵运算就可以恢复出发射端发送的信号，但是由于ZF均衡没有考虑噪声的影响，在消除干扰的同时也放大了噪声，造成通信系统的误码率性能下降，尤其是在信噪比较低的条件下。MMSE 均衡算法考虑了噪声的影响，其目标是使得发送端发射的数据与接收端估计的数据的均方误差达到最小，在低信噪比时MMSE 算法性能要好于ZF 算法，但是MMSE 算法需要噪声的先验知识，并且算法的计算复杂度较高。非线性均衡算法主要有判决反馈算法、最大似然算法和Turbo 迭代算法等。判决反馈均衡主要是通过常用的均衡准则预测和判决后干扰抵消［10］，能够有效减小码间干扰对系统性能的影响，提高数据传输的正确性，特别是在信道严重失真时非常适用。最大似然均衡算法主要是进行多次的搜索，寻找出接收向量和所有可能的后处理向量之间的最小欧氏距离，此时对应的向量就是均衡后的信号［11］。Turbo 均衡主要是通过反复均衡以及信道译码来得到发射信号的迭代算法［12］，由于要迭代计算，因此复杂度也非常高。

深度学习在处理大数据时性能优异，已有学者将深度学习应用于无线通信领域中［13-19］，例如数据检测［13-14］、信道估计［15-17］和CSI 反馈［18-19］。在文献［13］中，一种基于全连接（Fully Connected，FC）神经网络的数据检测算法被应用于OFDM 系统的接收端，这种算法将OFDM 和无线信道视为一个黑匣子，直接从接收数据中检测出发送数据；文献［14］提出一种滑动双向循环神经网络（Sliding Bidirectional Recurrent Neural Networks，SBRNN）结构的数据检测算法，主要应用在数据速率相对较低的分子通信中；在信道估计领域，文献［15-16］针对高速移动环境下单入单出（Single-Input and Single-Output，SISO）OFDM 系统下行链路信道估计性能受限的问题，采用深度学习来进行信道估计，提高了信道估计的性能，文献［17］将基于深度学习的信道估计算法扩展到了多入多出（Multiple-Input and Multiple-Output，MIMO）OFDM 系统，相较于传统算法有效提升了系统性能。以上文献仅仅研究了深度学习在信道估计环节的应用，而本文将信道估计和信道均衡进行联合考虑，进一步挖掘了深度学习在通信领域内的应用潜力。文献［18］将通信领域中相关理论与深度学习进行结合，提出了一种名为ComNet 的信道估计算法，它的收敛速度更快且解释性更强；此外，深度学习应用在MIMO 系统中的CSI 反馈相关工作可以在文献［19-20］中找到。根据调研可知，相较于传统算法，深度学习在无线通信中各个环节中都可以在一定程度上改善系统性能。

2 系统模型

随着通信技术的快速发展，人们更加追求高速、稳定的无线数据传输；另一方面，频带资源紧缺的问题也愈发严重。OFDM 通信系统采用多载波调制方式，提升了数据传输速率，并且能有效地对抗多径衰落的影响；正交子载波调制这种方法大幅降低了频带利用率，而且LET-V2X 标准中也采用了OFDM 技术。为了对比传统的分两个阶段进行信道估计与均衡的算法，本文中传统信道估计算法采用导频辅助估计的方法，在目前的研究中，采用较为广泛的导频图样有梳状导频图样、块状导频图样以及格状导频图样等［21］。如前文所述，在高速移动的通信场景中，信道呈现出双选衰落特性，相对来说，块状导频图样更适用于这种场景，所以IEEE 802.11p 以及LTE 等通信协议都采用了块状导频图样来辅助进行信道估计。本文采用块状导频图样及LTE 导频插入模式，基于LTE的OFDM帧结构具体如图1所示。

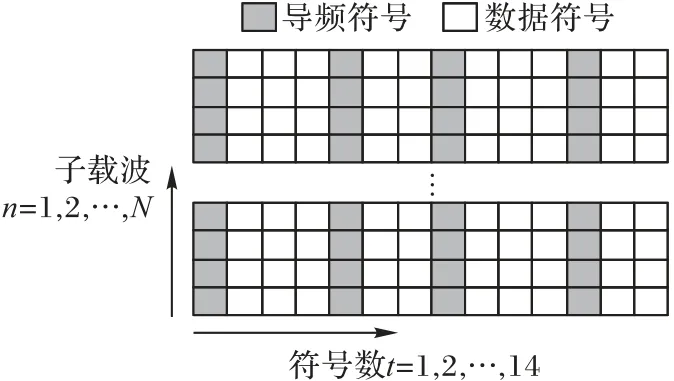
图1 基于LTE的OFDM子帧结构Fig.1 OFDM subframe structure based on LTE

考虑具有N个子载波的OFDM系统，一个子帧总共包含T个OFDM 符号，设第t个OFDM 符号上第n个子载波上传输符的符号用st(n)表示，因此第t个OFDM 符号上传输的符号矢量为。将频域符号经过逆离散傅里叶变换（Inverse Discrete Fourier Transform，IDFT）进行OFDM调制后，有

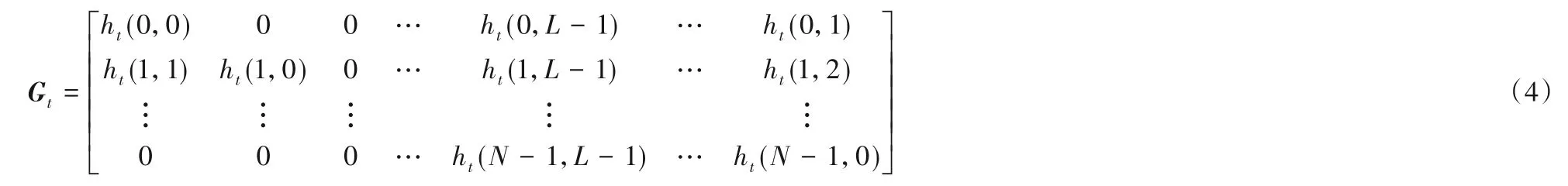
其中：L为多径数；ht(k，l)表示第t个符号时间上，信道冲激响应第l个抽头的第k个采样点。整个系统的信号处理框图如图2所示。

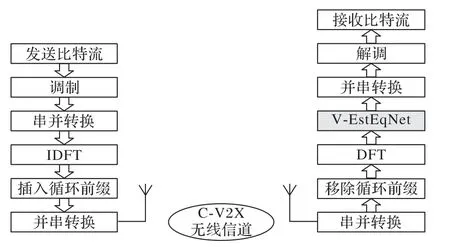
图2 系统信号处理框图Fig.2 Block diagram of system signal processing

在传统算法中，需要首先在信道估计环节获取到估计的，然后利用对接收数据yt进行均衡得到，而在本文算法中，利用深度学习网络在训练阶段从大量接收数据yt中学习到信道变化特性，进而在预测阶段直接从yt得到。

3 本文算法

本文算法V-EstEqNet主要包括一维（One Dimension，1D）卷积神经网络（Convolutional Neural Network，CNN），双向长短期记忆（Bi-directional Long Short-Term Memory，BiLSTM）网络和全连接神经网络（Fully Connected Neural Network，FCN），结构如图3所示。

图3 V-EstEqNet网络结构Fig.3 Network structure of V-EstEqNet

图3 中：1D CNN 网络和与其相连的第一个FCN 主要用于从接收数据中提取叠加的信道特征值，旨在提取信道特性；两个长短期记忆（Long Short-Term Memory，LSTM）单元分别用于正向和反向跟踪信道特性，对接收数据进行补偿和恢复；因为双向LSTM 的输出是具有正反两个方向的数据拼接，所以第二个FCN主要用于降维输出，即最终的估计数据。

通常来说，一个CNN 网络包含多个卷积核，这些卷积核可以视为卷积滤波器，每个卷积核在不同通道上处理该通道上的数据，通过滑动卷积核的位置对数据进行卷积求和。设W为卷积滤波器，其卷积核尺寸为l×w，其中l表示卷积核的长，w表示卷积核的宽。在数据上滑动滤波器，对总共lw个数据加权求和得到卷积输出。其变换公式可以表示为：

其中：b为偏置；f(⋅)为激活函数；*表示卷积操作。本文使用双正切激活函数，即tanh函数，其表达式为：

BiLSTM网络为两个单向LSTM网络的组合，其中：正向的LSTM 网络对信道特性进行正向跟踪，然后补偿和恢复数据；另一个LSTM 网络进行反向补偿。LSTM 网络主要由若干个LSTM单元组成，每个单元由输入门、遗忘门、输出门和记忆单元组成。遗忘门用于丢弃数据中的无用信息，输入门决定添加新的信息的量，输出门用于输出经过变换后的信息。LSTM网络具有内在的存储器单元，能够长时间保持先前提取的信息以用于下一个时刻的预测。单个LSTM的结构如图4所示。

在图4中，所涉及的计算公式有：

图4 LSTM结构Fig.4 Structure of LSTM

其中：it、ft、ot、ct、lt分别为LSTM 网络每个时间步的输入门、遗忘门、输出门、记忆单元和隐藏层矢量；Ui，Wi，Uf，Wf，Uc，Wc，Uo，Wo∈Rd×d为LSTM网络的权重矩阵；bi，bf，bc，bo∈Rd为LSTM 网络的偏置；⊙表示元素乘法；σ为sigmoid 激活函数；d表示输入序列维度，在本文中即为OFDM 子载波个数；t为输入序列长度，即OFDM 符号数，也是LSTM 单元数量。将式（7）～（11）进行组合，记为LSTM(⋅)，则可以将公式简化为：

其中：Θ表示LSTM 网络中的所有参数；Wl2o和bl2o表示隐藏层到输出的权重和偏置。本文使用两个方向相反的LSTM 单元对接收数据进行补偿，即BiLSTM，其输出变换公式可以表示为：

其中：为t时刻BiLSTM 网络的反向输出；pt为t时刻BiLSTM网络的输出；Concat(⋅)函数将两个矢量按指定维度结合起来。将BiLSTM网络每个时间步的输出变换简写成：

其中：为t-1 时刻BiLSTM 网络的反向隐藏层矢量为t时刻BiLSTM 网络的反向输入；Θbi和BiLSTM(⋅)分别表示BiLSTM 网络中的所有参数和变换函数。BiLSTM 网络的输出维度为单向LSTM 网络的两倍，因此在深度学习网络最后一层使用全连接网络对BiLSTM 网络每个时间步的输出进行降维，相较于卷积神经网络，全连接神经网络输入每个元素都连接到一个不同的权重，输出为输入所有的元素加权和。

在搭建好深度学习网络之后，要想使其具备从接收数据中恢复出发送数据的能力，必须对网络中的所有参数进行调整，这个过程称为模型训练。在本文中采用端到端的方式来训练V-EstEqNet，以获取网络中所有的权重和偏置。以往的研究中，学者们提出了许多信道模型，以便在信道统计方面很好地描述信道，可以利用这些信道模型通过仿真得到所需要的数据。

如图2所示，在t时刻，发送端首先产生一个随机比特流，经过星座点映射及OFDM 相关操作后的得到发送数据为st，发送数据经过信道以后，在接收端得到叠加了信道特性的失真数据yt。本文所提学习网络的输入即接收数据yt，发送数据st作为训练标签。特别要指出的是，这里的st是子载波映射之后的OFDM 子帧数据，且包含了导频数据；yt是在子载波解映射之前的OFDM 接收子帧数据。为了让本文所提出的V-EstEqNet 更好地跟踪信道特性对接收数据进行恢复，在训练网络时训练集的数据不考虑噪声的影响。由于神经网络需要以实数作为输入，首先需要对数据进行预处理，这里需要分别对训练数据yt以及标签st的实部和虚部进行拼接，数据的预处理的维度变化示意图见图5。

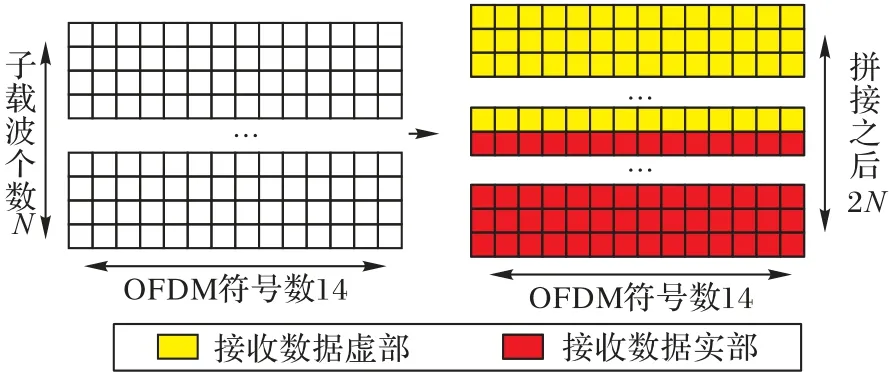
图5 数据预处理维度变化Fig.5 Dimension change of data preprocessing

这里考虑一个具有N个子载波的OFDM 通信系统，如前文所述，本文采用块状导频图样，导频数据位于OFDM 帧结构的1、5、8、12位置处，如图1所示。在一个OFDM 子帧中，共包含14 个OFDM 符号，本文中采用逐帧检测的方法，每当接收端接收到一个OFDM 子帧yt，就利用V-EstEqNet 对其进行校正和恢复。因此V-EstEqNet的输入是OFDM 接收子帧全部数据的实部和虚部，其维度为2N×14，对于标签数据st的处理也是相同的处理方法。

V-EstEqNet 所有层的激活函数均为tanh 函数，网络中的所有需要更新的参数使用自适应矩估计（ADAptive Moment estimation，ADAM）算法进行更新，ADAM 算法与传统采用固定学习率的梯度下降算法不同，它能够通过训练来自适应地更新学习率。在损失函数的选择上，本文采用均方误差（Mean Squared Error，MSE）损失函数，通过最小化神经网络的输出与训练标签st来训练网络，其公式为：

4 复杂度分析

本文中，1D CNN 卷积核的数量为2N，卷积核大小为3，步长为1；BiLSTM 包含2N个神经元；全连接神经网络为时序全连接层，即14 个时序上的接收数据共享同一组参数，包含2N个神经元。

表1 对比了不同信道估计算法与信道均衡算法进行组合之后的计算复杂度，这里以完成一个OFDM 符号数据信道估计和信道均衡处理所进行的实数乘法次数对复杂度进行衡量。

表1 各算法计算复杂度Tab.1 Computational complexity of each algorithm

在本文中，使用以下约定：LS_ZF（Least Squares and ZF）为在导频处使用最小二乘法（Least Squares，LS）进行信道估计，再根据导频处的估计结果对数据处进行线性插值完成整个信道估计；然后对信道估计的结果采用ZF算法进行信道均衡。LMMSE_ZF（Linear Minimum Mean Square Error and ZF）为在导频处使用线性最小均方误差法（Linear Minimum Mean Square Error，LMMSE）进行信道估计，再根据导频处的估计结果对数据处进行线性插值完成整个信道估计；然后对信道估计的结果采用ZF 算法进行信道均衡。LS_MMSE（LS and MMSE）、LMMSE_MMSE同理。

从表1 可以看出，V-EstEqNet 在线预测环节的复杂度尽管高于LS_ZF 算法和LS_MMSE 算法，但是与LMMSE_ZF 和LMMSE_MMSE 算法的复杂度处于同一个数量级内。这是因为神经网络仅仅是一些矩阵的乘法和加法操作，因此其复杂度并没有显著增加。此外，神经网络可以对数据进行并行处理，这也可以大大减少算法的运行时间。总体而言，VEstEqNet的算法复杂度处于可接受的范围内。

5 仿真分析

为对比V-EstEqNet 与其他传统算法的BER 性能。采用WINNER-II D2a［22］信道模型，训练时V-EstEqNet 的初始学习率为0.03，训练集的样本个数为10 000，批量大小为100，epoch为100。仿真系统参数如表2所示。

表2 仿真系统参数Tab.2 Simulation system parameters

5.1 静止状态时各种算法BER性能对比

C-V2X 的大多数应用场景都是终端在不断移动的情况，但是为了实验的完整性，本文从速度为0 的情况下开始进行仿真实验，在这种情况下发送数据受到的影响仅有码间串扰（Inter Symbol Interference，ISI）。图6为静止状态下V-EstEqNet与各个传统算法的BER性能对比。

图6 静止状态时的BER性能对比Fig.6 BER performance comparison in static condition

从图6 的仿真结果可以看出，随着信噪比（Signal-to-Noise Ratio，SNR）的升高，所有算法的BER 均在下降。相较于LS信道估计算法，LMMSE 信道估计算法在导频数据处可以获得更加精准的CSI，再配合线性插值方法完成整个信道估计的结果也会更加接近于真实的CSI，因此再经过均衡之后，在相同的信噪比下，LMMSE_ZF 和LMMSE_MMSE 的BER 性 能均好于LS_ZF 和LS_MMSE；而V-EstEqNet的BER 性能在低信噪比时（SNR 小 于6 dB 时），其BER 性 能 与LMMSE_ZF 和LMMSE_MMSE 效果相当，但是LMMSE 信道估计算法考虑了噪声的影响，需要先验知识，而V-EstEqNet 并不需要先验知识，也可以有与之相当的性能，这说明V-EstEqNet在对抗噪声时也有一定的效果；当SNR 大于12 dB 时，V-EstEqNet 的BER性能就随着SNR 的升高逐渐好于LMMSE_ZF 算法与LMMSE_MMSE算法。

5.2 运动状态时各种算法BER性能对比

当通信终端处于运动状态时，此时信道对发送数据的影响除了有ISI 以外，还会出现载波间干扰（Inter Carrier Interference，ICI）。运动速度越快，多普勒频移也越大，ICI 的影响也就越大。图7～10 分别是在速度为50 km/h、100 km/h、200 km/h、300 km/h时各种算法的BER性能对比。

从仿真结果可以看出，信道环境越恶劣，V-EstEqNet 的BER 性能就越好于传统的算法。如图7～8 所示，当速度为较低的50 km/h 和100 km/h 时，此时V-EstEqNet 相较于传统算法的LMMSE_ZF 与LMMSE_MMSE 最多有3 dB 的增益，相较于LS_ZF 与LS_MMSE 算法最高有6 dB 的增益。这说明本文所提出的V-EstEqNet能够学习到接收数据中所隐含的双选信道的特性，并根据这个特性来对数据进行校正和恢复。

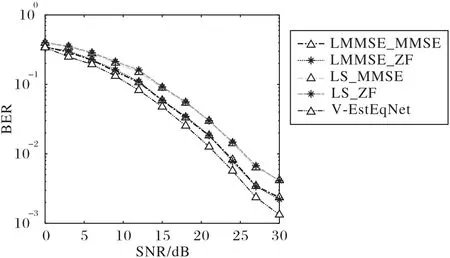
图7 速度为50 km/h时的BER性能对比Fig.7 BER performance comparison at 50 km/h speed

图8 速度为100 km/h时的BER性能对比Fig.8 BER performance comparison at 100 km/h speed

当速度处于较高的200 km/h 和300 km/h 时，此时发送数据所面临的ICI情况相较于低速情况下要更加严重，因此系统整体的BER性能比低速情况下要下降，尤其是在300 km/h时。在速度较高的情况下，传统信道估计算法配合线性插值的方法并不能很好地跟踪信道状态变化，导致获取到的CSI 误差较大，进而在信道均衡时引入了较大的误差，所以BER 性能较差，而本文所提的V-EstEqNet 首先经过了大量数据的离线训练，可以更好地跟踪信道状态的变化，所以表现出了更好的BER性能。如图9～10所示，当处于高速的环境中，V-EstEqNet在200km/h最多比LMMSE_ZF算法和LMMSE_MMSE算法高6dB的增益；而在300km/h时，V-EstEqNet 相较于LMMSE_ZF 算法和LMMSE_MMSE 算法的峰值增益则有9 dB。

图9 速度为200 km/h时的BER性能对比Fig.9 BER performance comparison at 200 km/h speed

图10 速度为300 km/h时的BER性能对比Fig.10 BER performance comparison at 300 km/h speed

由以上的仿真结果及分析可知，在不同的环境下，本文提出的基于深度学习的信道估计与均衡联合算法V-EstEqNet能够更好地适应信道环境，尤其是在高速移动的条件下。

6 结语

本文提出了一种面向LTE-V2X 的联合信道估计与均衡的深度学习网络，不同于传统的分两个阶段进行信道估计与均衡，本文将信道估计与均衡进行联合设计，从接收数据中直接恢复原始的传输数据。仿真实验结果表明，相较于传统算法，无论在静止条件下、低速条件下和高速条件下，本文算法V-EstEqNet 均有着较好的BER 性能，能够更加精准地从接收数据中跟踪信道特性，然后对接收数据进行补偿。