边缘计算支持下的移动群智感知本地差分隐私保护机制

李 卓，宋子晖，沈 鑫，陈 昕

（1.网络文化与数字传播北京市重点实验室（北京信息科技大学），北京 100101；2.北京信息科技大学计算机学院，北京 100101）

（*通信作者电子邮箱lizhuo@bistu.edu.cn）

0 引言

在移动群智感知（Mobile Crowd Sensing，MCS）系统［1］中，用户完成数据感知任务后向MCS 平台提交感知数据，用户的提交数据包括位置信息和感知数据。由于提交中的位置信息与用户的实际位置统一，任务感知结果反映出用户实际所处的真实环境信息［2］，导致用户提交数据存在泄漏用户隐私的风险。一方面，不同属性之间存在不同的用户隐私风险；另一方面，属性之间的关联也会暴露用户隐私。如地图信息感知任务，用户去指定地点查看该地点的建筑名称等信息并提交到MCS 服务器，感知数据为地名、建筑名等公共数据，但只对用户提交数据中的位置信息隐私保护，通过感知结果依旧可以泄露用户的位置隐私。

设计MCS 中的隐私保护机制比较复杂。不同于其他MCS 存在用户主动上传数据这一步骤，这一步骤增加了用户隐私泄露的风险；MCS 中的用户执行的感知任务多为公共数据，导致提交数据中的信息会与众多公开信息关联，进一步增加了用户隐私泄露的风险；同时无法保证MCS 服务平台的可信程度，隐私保护机制不仅要面向攻击者，同时也要面向MCS系统本身。

本地差分隐私（Local Differential Privacy，LDP）［3］保护是一种不依赖可信第三方、不受限于类型的数据隐私量化方法。LDP隐私保护的原理是对整体数据添加随机噪声达到保护个体数据的目的，因此在数据量相同的情况下，发布数据的有效数据比例减小。

综合考虑MCS 中用户提交数据的特点，本文针对边缘计算（Edge Computing，EC）支持下MCS 场景，基于本地差分隐私（LDP）保护原理设计出用户提交数据属性联合隐私保护的CS-MVP（Crowd Sensing with Multi-Value data privacy Protection）算法和用户提交数据属性独立隐私保护的CS-MAP（Crowd Sensing with Multi-Attribute data privacy Protection）算法。针对用户提交数据的多个属性，将属性关联为两部分：一是位置数据和感知结果数据的关联关系，该部分体现数据的可用性；另一部分为用户信息数据分别与位置数据和感知结果数据的关联关系，该部分体现了用户的隐私。CS-MVP 和CS-MAP 算法使得用户提交数据满足上述两部分所构建的LDP隐私约束模型。本文算法的主要优点如下：

1）用户仅需依据算法在本地对提交数据依概率替换，无需增加额外的交互和计算过程，且无需依赖可信第三方。

2）依据MCS 属性关联的LDP 隐私约束相较于LDP 数据隐私约束，避免了对单个属性数据进行大规模统计计算恢复原始感知数据的分布，用户提交数据中直接保留了可用性部分，增加了数据的可用性。

3）针对不同规模的MCS 任务类型设计了CS-MVP 和CS-MAP 两种隐私保护算法。CS-MVP 算法以属性联合的方法来增加隐私性，解决了随机扰动范围较小时，LDP模型的随机性降低造成的隐私性降低问题；CS-MAP算法以属性独立的方式增加数据可用性，解决了任务数量和感知数据范围较大的场景下，LDP模型的随机性增加导致数据可用性降低问题。

1 研究现状

针对MCS 中用户提交数据的隐私保护，当前研究主要集中在保护用户的位置信息和感知数据。

对于提交数据中的位置信息，由于用户在执行感知任务时，自身的位置与提交数据中的位置信息一致，因此，提交数据中的位置信息存在暴露用户位置隐私的风险，用户多次提交数据，可能泄露其轨迹。文献［4］研究虚拟位置技术，将用户的真实位置映射到一个虚拟的位置上来进行数据提交，但虚拟位置存在一些不合理的情况导致隐私性降低，且攻击者根据虚拟的位置和用户背景知识可推断出用户实际位置。文献［5］基于空间泛化技术提出了基于粒度的位置隐私保护算法，自适应地将用户位置泛化到不同粒度空间；在此基础上，文献［6］提出利用沃罗诺伊的概念来生成匿名区域；文献［7］提出一种位置K-匿名的算法，用一个包含K个用户的空间区域替代用户的真实位置，在这K个用户中，任何一个用户的位置都与其他K-1个用户的位置不可分辨。然而用户节点移动性会导致匿名区域的改变，从而使匿名区域面积过小不满足隐私保护要求，或过大降低位置准确性。

文献［8］提出基于区域覆盖数量的中心化差分隐私保护技术，以单位区域中的用户数量来构建差分隐私保护模型，对城市人口流量数据中的个人位置进行保护；文献［9］定义密度约束来计算出整体感知用户位置信息的全局敏感度，构建满足差分隐私的拉普拉斯噪声分量，对整体感知数据的中的位置信息进行差分隐私保护。

提交数据中的感知数据，包含数据类型复杂，且与用户所处环境密切相关。感知数据本身会泄露用户隐私，属性之间的关联也存在隐私泄露的风险，因为通过感知数据可间接获得用户当前位置信息。为降低由用户提交数据导致的用户隐私泄露问题，文献［10］利用多级代理机制，在不可信移动感知平台之间构建代理服务器，并提出了一种新的差分隐私保护机制使得用户数据满足差分隐私约束来保护用户身份隐私；然而这种方式无法保证多级代理之间的可信程度，代理之间可能联合从而使用户隐私泄露。文献［11］设计了一个对数据隐私保护下的移动群智感知系统架构，利用多个功能实体间的相互协作，实现了节点授权验证、节点匿名提交数据、数据隐私验证、用户匿名激励发放等功能。该方法虽然可实现完整的匿名数据提交和匿名数据评估，但将系统功能分散为多个实体增加了系统复杂程度，用户认证、令牌加密等算法也增加了计算复杂性。

LDP 技术由于不受数据类型的限制，已有多项工作使用LDP 技术来保护社会感知数据［12-13］。文献［14］基于Copula 函数构造满足LDP 的多维度群智感知数据。文献［15］提出LoPub 算法，构造多维本地差分隐私扰动机制来解决多属性下的节点隐私保护机制，利用统计计算方法，从多维联合分布中计算出单一属性的边缘分布情况。文献［16］提出面向Key-Value 类型数据的隐私发布机制PrivKV 算法，对Key 属性和Value 属性的数据分别进行LDP 扰动，并提供数据统计算法从被隐私化的数据中分别计算Key的频数和Value的均值。然而，这些算法均只针对通用数据类型来设计隐私保护机制，没有考虑MCS系统中用户提交数据的特点。

本文基于边缘计算支持下的MCS，提出CS-MVP 和CSMAP 用户提交数据隐私保护算法，基于MCS 中用户提交数据的属性关系，构建两种关系之间的LDP隐私约束，不但应用了LDP 理论在隐私保护上的优势，同时避免了在数据恢复时复杂的统计计算。

2 模型定义

本章定义MCS 的系统模型，并给出用户提交数据的隐私性模型和任务数据的可用性模型，提出隐私约束下的可用性最大化问题。

2.1 移动群智感知用户原始感知数据和提交数据模型

首先将用户采提交据构建为数学模型。设MCS 中感知任务位置集合L={l1，l2，…，lN}，感知任务结果的取值范围X={x1，x2，…，xM}，原始感知数据可表示为r=(l∈L，x∈X)，则任意用户ui的提交数据记作di=

2.2 多属性用户提交数据的本地差分隐私模型

用户的原始感知数据可以为任意位置和任意感知数据的组合，即r∈R，其中R为L和X中所有元素对应构成组合的集合。

任务执行后，用户获得正确的原始感知数据ri∈RT。一组能保证任务完成的原始感知数据集合RT是R的一个子集，RT⊂R。RT表示所有位置li与用户实际在该位置感知到的结果xi的组合的集合。

构建满足LDP的用户原始感知数据和发布数据模型。存在隐私保护算法Q，其定义域和值域分别为RT和R，满足：

存在隐私保护算法QX，其定义域和值域均为X；隐私保护算法QL，其定义域和值域均为L，满足：

则算法Q满足隐私预算为ε的用户数据属性联合的本地差分隐私保护，QX、QL满足隐私预算为ε的用户数据属性独立的本地差分隐私保护。

2.3 用户隐私化提交数据的可用性模型

用户真实的提交数据集合D={d1，d2，…，di，…}。对D中所有数据采用相同的隐私保护算法，构建隐私化提交数据集合D'={d'1，d'2，…，d'i，…}。

设D对应的原始感知数据RT中存在ra=，ra∈RT，D'=Q(D)，则集合D'中任意r'∈R的概率为：

对于隐私化的用户提交数据，相同位置中正确数据的概率大于错误数据的概率时，可保留正确感知数据信息。即D'中包含ra的数据的概率大于仅包含数据la的概率：

定义隐私保护算法Q生成的数据满足MCS 任务可用性指标I：

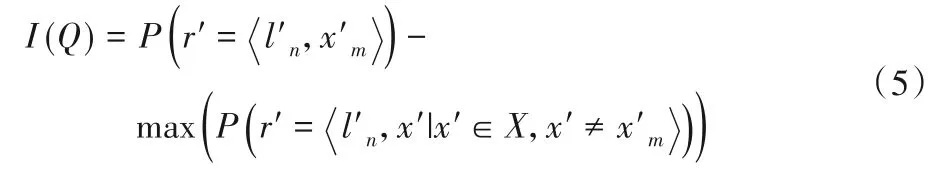
基于LDP 隐私模型，可用性指标I反映了能从提交数据中恢复正确感知数据的概率。

2.4 隐私约束下的可用性最大问题

MCS 中用户发布数据隐私约束下的可用性最大问题可记作：

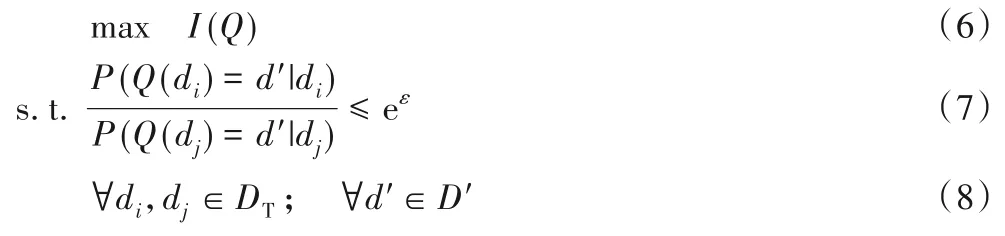
3 EC支持下的用户提交数据隐私保护算法

3.1 EC支持下的移动群智感知系统流程

为分离用户和MCS 云服务器的直接交互，消除MCS 云服务器泄露用户隐私的风险，在MCS 中引入边缘计算架构。同时，满足LDP的隐私保护算法［17-20］对原始感知数据［21-22］隐私处理后会生成部分噪声数据，隐私预算越高，提交数据中的噪声数据越多，引入边缘服务器，在靠近用户端计算恢复出任务需求数据，过滤掉用户提交数据中相同任务的噪声数据，降低MCS系统数据传输成本。

基于边缘计算架构设计了MCS系统流程如图1所示。任务分发阶段，云服务器向边缘服务器发布感知任务，由边缘服务器代替云服务器对用户进行任务分发，用户执行的具体感知任务对云服务器保持隐私性；任务提交阶段，用户首先利用满足LDP的隐私保护算法，本地处理原始感知数据，然后提交隐私化的感知数据给边缘服务器；边缘服务器聚合所有用户提交数据，通过统计计算恢复任务结果提交云服务器。

图1 边缘计算支持下MCS用户数据隐私保护流程Fig.1 Flow of MCS user data privacy protection supported by EC

整个过程中云服务器不直接接触用户数据，而边缘服务器接触到的为用户满足LDP 隐私的提交数据，因此保证了用户隐私。

3.2 CS-MVP算法

本节介绍满足LDP的用户提交数据属性联合隐私保护算法的设计。属性联合即将用户提交数据中的位置和感知结果属性组合成的数据作为整体构建隐私约束。隐私化的发布数据符合用户提交数据取值范围且满足LDP隐私约束。

设L中位置的数量为N，感知任务的取值范围X的元素数量为M，则集合R中的元素个数为M×N。属性联合的原始感知数据的取值范围为RT，隐私化的用户提交数据中感知数据的取值范围为R。Q为RT到R的随机转移矩阵。

考虑感知任务执行前RT未确定。首先构建由R向R的随机转移矩阵QR。QR的元素为条件概率qij=P(rj|ri)。

QR应满足以下约束：

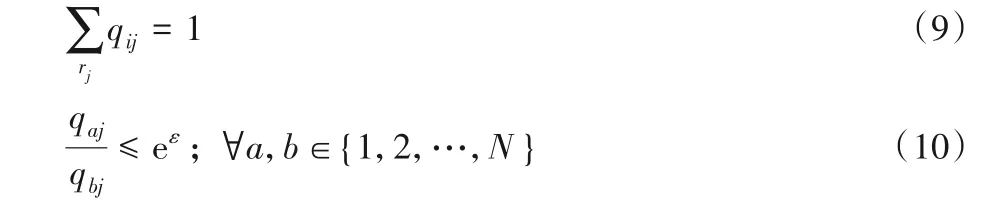
式（9）表示任意元素ri变换为rj所有可能取值的概率和为1；式（10）表示该变换满足隐私预算为ε的LDP隐私约束。

用户提交数据可用性为：

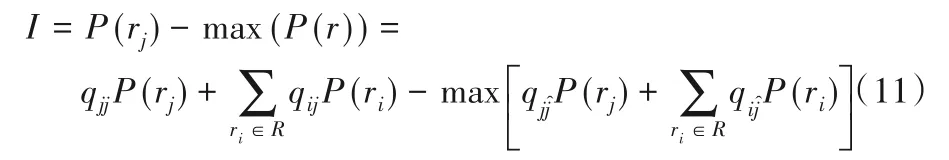
在每个位置感知相同的数据量的情况下，问题（6）可转换为：

求解可得：

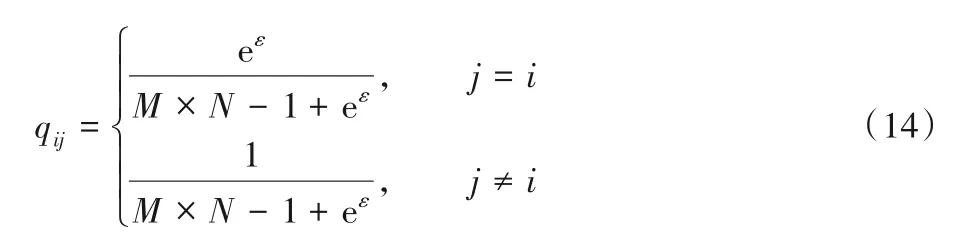
任务执行后，每个用户依据其原始感知数据，选择QR对应的行，所有被选择的行组成由RT向R的实际使用的转移概率矩阵Q。如图2所示。

图2 基于随机转移矩阵的MCS用户提交数据的隐私算法Fig.2 Privacy algorithm of MCS user submitted data based on random transition matrix

实际的状态转移矩阵Q依据真实的感知结果来构建，在任务执行前，边缘服务器根据隐私预算，首先构建完全随机转移矩阵QR，用户在感知结束后选择需要的行对原始感知数据随机变换。隐私化的用户感知流程为：

1）边缘服务器计算感知任务位置数量N，感知数据取值范围元素个数M。

2）边缘服务器生成用户原始感知数据取值范围和提交数据取值范围R：

3）边缘服务器计算转移概率参数a=M×N-1+eε。

4）边缘服务器生成完全随机转移矩阵QR，其元素值为：

5）用户执行感知任务，获得原始感知数据ri，从QR中选择第i行对ri随机变换得到隐私算法的发布数据r'，生成用户提交数据=

属性联合的MCS 用户提交数据隐私保护算法将用户的原始感知数据随机变换到取值空间中任意值，该算法可直接保留位置和感知结果的对应关系。对于同一个任务位置，虽然取值空间存在多个值，但MCS 的用户原始感知数据中，相同位置只存在唯一值，CS-MVP 算法将个体数据随机化，扰乱了数据整体分布，但原始数据保持了最高的后验概率，因此恢复算法仅需统计提交数据的频数即可恢复真实结果。

CS-MVP算法为用户提交数据提供了严格的隐私性，但该算法中数据的取值空间大小为任务量和所有任务结果取值空间大小的乘积，当任务量过多或任务取值范围过大时，提交数据的取值范围也将扩大，这导致原始感知数据恢复算法需求的样本量增加。为解决联合隐私造成的取值空间相乘性扩大问题，本文另外提出了属性独立的MCS 用户提交数据的本地差分隐私保护算法。

3.3 CS-MAP算法

本节介绍属性独立的用户提交数据的本地差分隐私保护算法。将用户提交数据中位置属性数据和感知结果数据独立地进行隐私保护，可降低多个属性取值空间相乘引起的提交数据取值空间的扩大。MCS中任务需求为位置数据和感知结果数据之间的对应关系，因此，设计属性独立的MCS 用户提交数据隐私保护机制需要在保证不同属性独立隐私约束的情况下保留位置和感知结果数据的对应关系，以保留提交数据的可用性。

仍针对上述场景，所有任务的位置L的数量为N，感知任务的取值范围X的元素数量为M。属性独立的本地差分隐私算法即构建由状态空间L到L的转移矩阵QL和由状态空间到X的随机变换矩阵QX。其中QL和QX的元素分别为

对于任意原始感知数据ra=，为保持生成提交数据中la和xa的对应关系，基于独立状态转移，设计了两阶段的转移过程：第一阶段，对ra=做随机扰动，若生成数据为ra=，则用户用原始感知数据构建提交数据；若生成数据为虚假数据，则执行第二阶段。第二阶段，构建虚假数据，分别从集合L和集合X中去掉la和xa，然后以均匀分布分别从中选出的数据构建用户的提交数据。

基于上述步骤，可保留原始感知数据中位置和感知结果的对应关系，即保留了用户提交数据的可用性，并且可得出如下约束条件：

其中：式（17）为在两个属性独立变换过程中保持正确数据的概率相同，且若在变换过程中位置保持不变，则此时感知数据也应保持不变；式（18）为位置和感知数据独立变换的约束，类比式（9）；式（19）属于独立的LDP隐私约束。

用户提交数据可用性为：

属性独立的本地差分隐私保护算法，对用户原始感知数据中的不同属性数据独立扰动，提交数据的取值空间相较于属性联合算法降低了样本需求量；但属性独立算法只对数据的属性满足差分隐私约束，对用户提交数据不满足严格的隐私约束，相较于联合算法隐私性降低。

3.4 基于差分隐私发布的感知数据恢复算法

本文所提出的CS-MVP 算法和CS-MAP 算法均依据MCS用户提交数据属性间关系分析和处理，扰乱用户信息与位置、感知结果的对应关系，保留位置与感知结果的对应关系。边缘服务器汇总所有用户的提交数据，计算恢复任务感知数据的算法不需要经过复杂的统计计算，根据用户提交数据可用性最大化，只需要计算提交数据中相同位置数据中频数最大值即可。具体流程如算法3所示。

汇总所有用户的提交数据，提交数据中携带的隐私化任务感知数据属于取值空间R，将提交数据按取值空间R计数，记录每个可能取值的频数；然后按相同位置将R划分，对每个位置取频数最大的元素，作为恢复的感知结果。

4 理论分析

4.1 算法的时间复杂性

根据算法1和算法2可分析得算法的时间复杂度。

定理1CS-MVP 算法的时间复杂度为O(MN)，CS-MAP算法的时间复杂度为O(max(M，N))。

算法1 中感知任务位置集合L，感知数据取值范围X，采用嵌套循环，外循环共循环N次，内循环共循环M次，则双重循环的时间复杂度就是O(M×N)。类比算法1，算法2 中第4）步构建QX和QL的时间复杂度均为max(M，N)，同时第6）步中用户遍历QX和QL，即MAP 的算法复杂度为O(max(M，N))。

4.2 数据隐私性

定理2算法CS-MVP 的一组发布数据对其原始感知数据满足隐私预算为ε的LDP约束。

证明 依据随机转移矩阵，可得发布数据中任意r'∈R来自于原始感知数据r∈R的转移概率P(r'|r)，

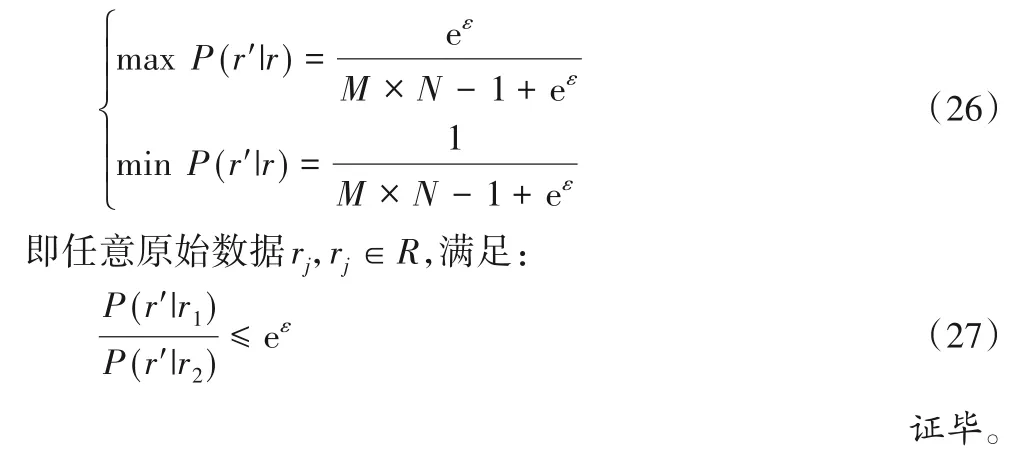
定理3算法CS-MAP 的一组发布数据对其原始感知数据的位置数据和感知结果属性分别满足ε的LDP约束。

证明 发布数据中任意r'=∈R，由原始感知数据变换来的转移概率为：

其为原始感知数据中任务位置属性到la的转移概率，可知对于任意原始数据中位置属性数据li(lj∈L)满足：

对于任意原始感知数据中感知结果属性数据xi，xj∈X满足：

定理4算法CS-MAP的任意发布数据r'∈R对其原始感知数据r∈RT满足隐私预算为ε+ln(min(M，N) -1)的LDP隐私约束。

存在如下等式：

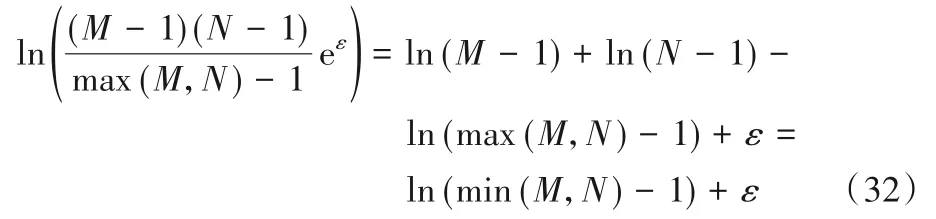
概率比的满足如下：

4.3 数据可用性

对于最优机制，不同任务之间的数据不受任务实际数据如何取值影响，即对任意任务所有可能取值，由其他任务变换而来的概率应相同。公式如下：

5 实验与结果分析

基于Python 环境使用真实数据集GeoLife［23］对算法进行性能评估。GeoLife 数据集是由微软亚洲研究院于2016 年发布的北京地区的轨迹信息，其中主要包含182 个移动设备的17 621 个轨迹数据。将统计相同时间段和一定区域范围内的设备数量作为感知任务，共提取出1 134个感知任务与感知数据对。同时实现了LoPub和PrivKV算法作为对比。

感知数据的可用性表现为真实数据与噪声数据生成概率的差值，随着样本量增大，概率接近于数据频率。可用性越大，正确数据与错误数据的概率差值越大，即样本频率差值越大。即可用性越高，计算获得真实感知数据所需的用户提交数据数量越少。定义数据样本比（Data Sample Ratio，DSR）为所有任务获得的感知数据的平均个数。实验验证在不同隐私预算和DSR 下，计算感知数据的准确率。使用0-1 损失函数来度量统计值和原始值的误差。

任务的平均数据准确率记作：

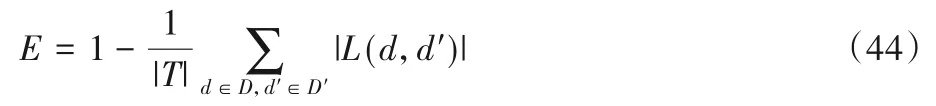
将隐私预算控制在［0，10］，DSR 控制在［0，5 000］。对实验中的每个状态均计算10次结果后取均值。

首先分析在不同DSR 和不同隐私预算下，CS-MVP 和CSMAP算法的平均数据准确性，验证算法的适用范围。

如图3 所示，当隐私预算大于3.5，每个任务平均采集数据量大于300 时，CS-MVP 算法恢复任务结果的准确性大于95%；在隐私预算大于2，每个任务平均数据采集量大于200时，CS-MAP 算法恢复任务结果的准确性大于95%。CS-MAP算法比CS-MVP 算法具有更大的隐私预算适用范围，且在相同隐私约束下，需要采集的数据量更少。

图3 CS-MVP和CS-MAP算法生成数据的平均准确率Fig.3 Average accuracies of data generated by CS-MVP and CS-MAP algorithms

利用CS-MVP 和CS-MAP 算法顺序隐私化处理多个数据，对比运行时间，每次实验统计10 次处理时间取平均值，实验结果如表1所示。从表1可看出，两算法的运行时间随着数据量的增加差距逐渐增大。在数据量为1 000 以内时，CS-MAP算法的运行时间0.04 s以下，而CS-MVP算法的运行时间最长已超过20 s。属性独立的随机算法可显著降低算法的运行时间。

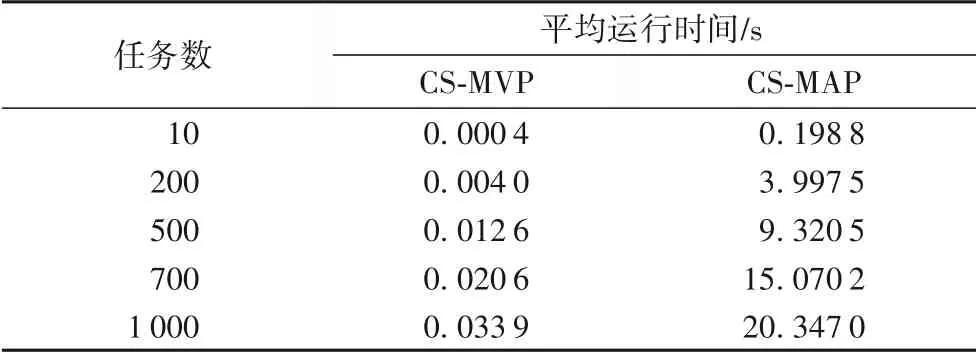
表1 CS-MVP和CS-MAP算法的平均运行时间Tab.1 Average running times of CS-MVP and CS-MAP algorithms

实验过程中实现了LoPub 和PrivKV 算法来对比CS-MVP算法的性能。分别在隐私预算ε=2，4，6 三种情况下，对比CS-MVP、CS-MAP、LoPub 和PrivKV 四种算法随着DSR 增加生成数据的准确性。

如图4 所示，随着数据量的增多各算法生成数据的准确性逐渐增加；对满足LDP 的隐私保护算法，隐私预算增加，隐私性降低，数据可用性增加，图4 中体现在随着隐私预算的增加，在数据达到相同隐私预算下，需要的DSR越小。

从图4 可明显看出，在相同条件下，CS-MAP 算法的准确性大于CS-MVP 算法和PrivKV 算法的准确性。在隐私预算ε≥2 时，CS-MVP 算法的准确性比PrivKV 平均高40%。原因在于：PrivKV是对数据进行二值差分隐私扰动，其发布值的隐私空间小，在隐私性低的情况下能保持较高的可用性；而CSMVP 机制的发布空间为感知数据所有可取值空间，发布值取错误值的概率更大。整体来看，CS-MVP直接从提交数据中计算两个属性数据间的对应关系，而PrivKV 需要统计频次计算分布来得出真实值，因此需要更多的数据量来支撑。

在隐私预算为2 和4 时，CS-MVP 算法的数据准确性比LoPub 高30%；在隐私预算为6 时CS-MVP 算法略低于LoPub算法，其原因在于LoPub 算法发布值的取值空间也为感知数据的所有取值，在隐私预算小时，可用性较低，且需要计算数据的整体分布，然后从中再恢复对应关系，因此需要的数据量较多，在相同数据量下，准确性低于CS-MVP。两种算法的准确率在隐私预算增大时表现得逐渐相等，如图4（c），但LoPub算法需要多次迭代操作来逼近结果，算法复杂度要远大于CSMVP。图4（b）中在样本量大于20 后，CS-MVP 的准确性大于LoPub，其原因在于，LoPub是利用EM（Expectation Maximization）算法计算分布，EM 算法迭代过程中预设初始分布为均匀分布，群智感知结果分布与均匀分布相差较大，计算的任务数据准确率较低。

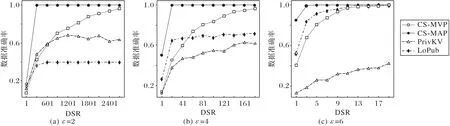
图4 CS-MAP、CS-MVP、PrivKV、LoPub生成数据的准确性对比Fig.4 Accuracy comparison of CS-MAP，CS-MVP，PrivKV，LoPub generated data

最后，CS-MAP的算法的数据准确率在三种情况下均大于其他三个算法，且在较低的隐私预算下也能保持较高的数据准确性。原因在于该算法发布值的空间只在每个属性的各自独立空间中，且直接保留了位置和感知结果的对应关系。从图4 可知，CS-MAP 算法比LoPub 算法的数据准确率平均提高了26.94%，比PrivKV 算法平均提高了84.34%；CS-MVP 算法比LoPub算法平均提高了66.24%，比PrivKV 算法平均提高了144.14%。

接下来验证边缘计算模式支持下隐私保护的MCS 系统感知开销。保持用户提交的感知数据量不变，分析网络中的数据传输量。记Ce为边缘计算支持下的传输数据量，Cc为不引入边缘计算模式时的传输数据量。传输数据降低比记作：

在保证感知数据恢复准确性大于95%的情况下，实验结果如图5所示。

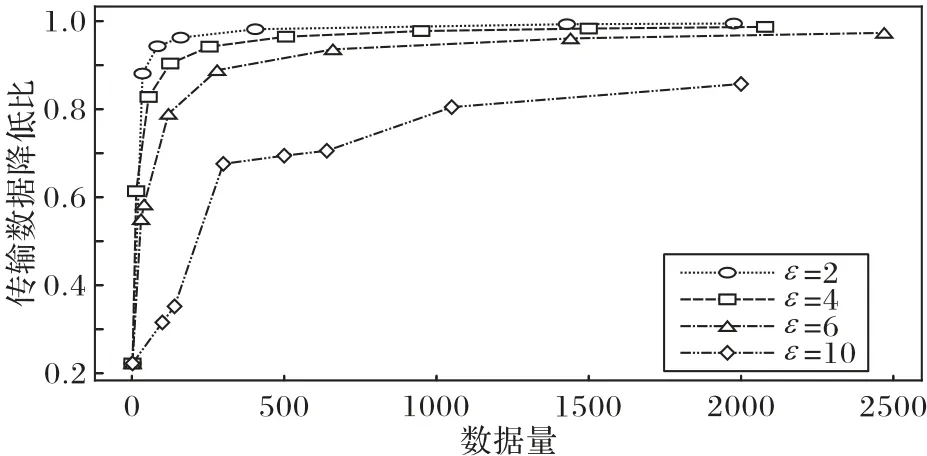
图5 边缘计算模式对MCS系统数据传输量的影响Fig.5 Influence of edge computing mode on data transmission amount in MCS system

从图5 可知，随着提交数据总量的提升，边缘计算可显著减少数据传输量。边缘计算服务器汇聚所有隐私算法生成的发布数据，忽略随机算法生成的错误数据，只向云端传输实际任务数据，当平均任务数据DSR 大于10 时，对每个任务采集10 个以上的感知数据，而只向云端传输一个数据，可降低90%网络中的数据量，这与实验结果相符合。

6 结语

本文针对MCS 用户数据提交阶段隐私保护困难和因隐私保护带来的成本增加问题，建立了用户提交数据的隐私性和任务数据可用性模型，设计了基于用户提交数据属性关系的CS-MVP 算法和CS-MAP 算法。在MCS 中引入边缘计算架构，设计了边缘计算支持下的隐私化MCS 系统感知模式。针对MCS 用户提交数据可用性的下界进行理论分析，证明CSMVP 算法在数据属性联合隐私约束下的最优性，CS-MAP 算法在数据属性独立隐私约束下的最优性，并定量给出CS-MVP和CS-MAP 算法生成数据的可用性。实验结果表明，与现有的LoPub 和PrivKV 算法相比，在相同隐私预算下，CS-MVP 和CS-MAP 算法拥有更高的数据准确性和更低的数据量需求。CS-MAP 算法较之CS-MVP 算法拥有更高的数据可用性和更低的算法复杂度，但其隐私约束局限于一组任务数据，对存在多组感知数据的用户数据不满足隐私约束。边缘计算的引入可减低MCS 系统中90%的数据传输量。在当前工作的基础上，未来拟开展隐私保护下的MCS 任务分发和激励机制的优化研究。