利用随机多项式展开的海底声学参数反演方法

李风华 王翰卓

1) (中国科学院声学研究所, 声场声信息国家重点实验室, 北京 100190)

2) (中国科学院大学电子电气与通信工程学院, 北京 100049)

为了提高地声反演算法的计算效率, 探索克服地声反演结果多值性问题, 本文利用宽带、多收发位置的传播损失数据结合传播损失在地声参数先验搜索区间内的随机多项式展开系数矩阵, 反演得到海底纵波声速、吸收率和密度比重.使用随机多项式展开近似传播损失时, 展开系数的自变量为声波频率、收发位置等参数, 随机多项式的自变量为表示声速、吸收率、比重在各自搜索区间内均匀分布的随机变量.传播损失的展开系数通过嵌入随机多项式的声学宽角抛物方程结合盖辽金投影、最小角度回归算法计算求得.在低频、一定声传播水平距离以内和地声参数搜索区间长度适中时, 使用随机多项式展开近似传播损失的相对误差在1%以下.仿真发现, 在浅海环境中使用低频、一定声传播水平距离以内的传播损失数据, 在接收信号信噪比较高、声源和水听器相对位置误差较小时, 选择合适的随机多项式展开截断幂次可较准确地反演海底声速、吸收率和密度比重, 且计算效率比网格遍历搜索方法提高一个数量级以上.

1 引 言

海洋声学中的逆问题是利用海水中声波所携带的声源位置及海洋信道环境特性信息, 对声源位置和介质参数进行求解.地声反演问题是快速获取局部海域等效海底声学参数的方法, 是水声逆问题的重要研究方向[1].地声反演过程需要进行以下几个方面的内容: 海底环境模型选取, 待反演参数搜索范围的确定, 拷贝声场计算, 匹配物理量及代价函数的构造, 最优化算法的选取, 反演结果的评价.为求解待反演参数的全局最优值, 需要采用遍历或最优化算法在待反演参数空间内反复选取待反演参数向量、计算其对应的拷贝声场以及代价函数.传统基于遍历搜索方法所需计算量大, 计算时间长;代价函数对部分待反演参数的不敏感以及待反演参数在代价函数中的耦合效果使得代价函数存在多解性问题[1].提高反演速率以及克服多解性是地声反演中需要解决的问题.

为了减少求解反演参数空间拷贝声场的计算规模, Gerstoft[2,3]和Dosso[4,5]分别提出了基于遗传算法和模拟退火的贝叶斯推断法, 该方法可快速求解作为代价函数的后验概率密度; Sambridge[6]提出了邻域插值近似方法, 该方法利用集合信息指导参数空间的重采样, 从而减少了计算量.

为了解决地声反演中的多值性问题, Holland和Osler[7]提出了组合反演方法, 将空间-时间域和空间-频率域的数据结合起来, 采用多种不同的地声模型拟合同一数据集.李整林等[8−13]在综合分析简正波的频散特性、海底反射系数、传播损失等声场特性的基础上, 应用匹配场处理器、自适应时频分析算法和并行遗传算法提出多物理量联合地声反演方法.

随机多项式展开法[14]是一种表示方程中的多维随机参数在方程解中非线性传递函数关系的方法.近些年引入到海水声速起伏[15−23]、海底参数不确知[22−25]、声源和接收点深度不确知[25,26]的声场建模中.随机多项式展开方法将频域复声压信号表示成以随机多项式为基底的级数展开形式, 随机多项式的自变量即为描述不确知(或随机)环境的随机变量.在地声反演问题中, 假设待反演参数为在搜索区间内均匀分布的随机变量[24], 通过随机多项式展开可以得到声场关于待反演海底参数的解析表达式.该方法的计算效率较遍历方法高, 可以作为计算拷贝声场的“代理”模型.

本文利用宽带多收发位置的声传播损失数据,结合地声参数搜索区间内传播损失函数的随机多项式展开系数矩阵, 求解随机多项式基底的数值,利用基底中的一次幂项, 唯一地反演海底声学参数.该方法比传统遍历搜索法计算速度快, 且对信号噪声和收发距离随机误差有一定的稳健性.

2 海底参数不确知下声场的随机多项式展开

在频率为f, 二维柱坐标水平和深度位置(r,z)处, 海底参数在各自区间内取值对应的向量为时, 频域复声压可以用随机多项式展开方法表示为

其中 k0是参考波数;{γq(f,r,z);q=0,1,···,Q−1}为随机多项式展开的系数, 是频率f和空间位置(r,z) 的函数;是随机多项式展开基, 是随机变量的函数; N是复声压的随机多项式展开中展开基的截断幂次; Q代表展开截断幂次为N时, 复声压的随机多项式展开项数.在均方意义下, 在截断幂次 N →∞ 时, 频率复声压的随机多项式展开近似结果可以收敛到真实值, 误差随着截断幂次N的增加指数减小[14].随机多项式基底有勒让德多项式的函数形式, 满足加权正交归一化条件:

其中 µ 为常数, 约为0.0366; κe(f) 为复波数平方的随机多项式展开系数; 随机多项式展开基与(2)式中复声压的展开基为同一组，M是复波数的随机多项式展开中, 展开基的截断幂次, 要求M < N,在计算中通常取M = 2; E代表展开截断幂次为M时复波数的随机多项式展开项数.

为了求解(2)式中的复声压随机多项式展开系数 { γq(f,r,z);q=0,1,···,Q−1} , 将(2)式代入到声学抛物方程(4)式后采用盖辽金投影法[14],在等式两端依次正交上随机多项式展开基的每一项, 获得展开系数 { γq(f,r,z);q=0,1,···,Q−1} 满足的方程组,可求得不同位置 ( r,z) 处, 复声压随机多项式展开系数 γq(f,r,z) 的数值[14,28].利用(1)式中海底声速、吸收率、比重与随机变量的关系, 将(2)式中的替换成得到复声压关于海底参数的解析表达式

浅海声传播中传播损失是对地声参数较敏感且易于观测和计算的物理量, 传播损失定义为接收位置 ( r,z) 处声压与距离声源位置1 m处的声压 P0幅度之比的分贝形式,表达式为

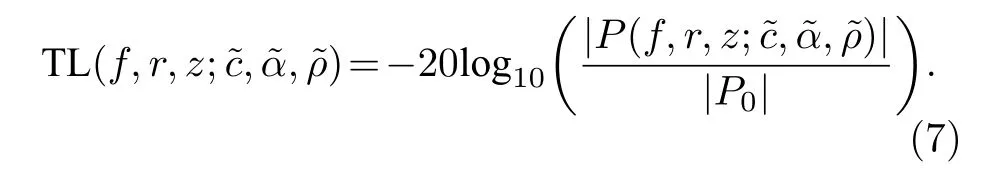
如(8)式所示, 声传播损失同样可表示为随机多项式展开形式, 其中展开系数为 { ιq(f,r,z) ; q=0,1,···,Q−1}.关于传播损失展开系数的计算,需对(2)式中的海底参数(对应到各随机变量)进行拉丁超立方采样[29], 利用(2)式中复声压的随机多项式展开近似结果以及(7)式中声传播损失的表达式, 获取大量地声参数-传播损失的训练样本, 采用稀疏自适应最小角度回归[30]计算得到传播损失的随机多项式展开系数 ιq(f,r,z).

3 基于声传播损失随机多项式展开的地声反演方法

依照以上的理论建模, 可以在一定条件下获取声传播损失关于声速、吸收率、比重在一定不确知区间内的解析表达式.本节讨论利用多频点、多收发水平距离的声传播损失随机多项式展开系数矩阵, 获取地声参数的反演算法.

为了书写方便, 假设接收深度z是统一的,(8)式中, 随机多项式展开方法把频率为 fi, 收发水平距离为 rj, 在地声参数搜索区间内的声传播损失 T L(fi,rj;表示成了Q项随机多项式展开项的叠加.对于有F个频点、R个收发距离的声传播损失, 可以将(8)式写成矩阵形式, 如(9)式.其中的展开系数 { ιq(fi,rj);q=0,1,···,Q−1 ;i=1,2,···,F;j=1,2,···,R}组成系数矩阵随机多项式 { pq;q=0,1,···,Q−1} 记成向量; 对应的传播损失 { TL(fi,rj) ; i=1,2,···,F;j=1,2,···,R}记为向量

其中 p0是常数项, p1p2p3分别是声速、吸收率、比重的一次幂函数.q >3 时,是各地声参数的高次幂项及交叉项.

若实验区域海底真实的声速、吸收率、比重参数为c,α,ρ, 实验获取的传播损失向量为在先验搜索区间内, 计算得到的随机多项式展开系数矩阵为可使用线性方程组求解方法计算随机多项展开基的数值:

4 反演仿真计算与评估

4.1 声场随机多项式展开的计算精度和效率

上述算法可以成功反演海底参数的前提是(2)式和(7)式中复声压和传播损失的随机多项式展开级数可以精确地近似其真值.为了方便讨论(2)式中不同截断幂次下随机多项式展开表达声信号的精度[31], 首先假设声压为平面波的情况,(14)式是声速和吸收率随机均匀分布的介质中, 平面波复声压的随机多项式展开.

研究得到, (14)式中当声速、吸收率的分布区间,随机多项式展开的截断幂次一定时, 平面波复声压的相对误差正比于频率、水平传播距离; 误差上限一定时, 随机多项式展开截断幂次越大, 可预报的频率f越高、距离r越远.图1给出随机多项式展开在不同截断幂次下, 频率-距离平面上复声压相对误差等于1%的等值线图.可以看出, 误差小于1%的最远距离r (单位为km)与最高频率f近似满足 r ∝f−1, 如频率 f =50Hz , 误差小于1%的

图1 不同截断幂次下, 在“频率f-距离r”平面上随机多项式展开平面波声压相对误差1%的等值线.其中声速的范围是1645−1655 m/s, 吸收率的范围是0.55−0.65 dB/λFig.1.Isolines of 1% relative error about sound pressure for plane wave expanded by the polynomial chaos in frequencyrange space.The intervals of sound speed and attenuation are 1645−1655 m/s and 0.55−0.65 dB/λ, respectively.

最远距离r为2.9 km.

在实际波导下的声传播环境中, 声压由多个模态干涉叠加产生.以浅海Pekeris波导为例, 对随机多项式展开的计算精度和计算效率进行分析.其中海底声速、吸收率的范围同上, 比重的范围在1.4—2.0.波导的水文环境和声源参数如表1所列.

表1 Pekeris波导的水文环境和声源参数Table 1.Hydrological conditions of Pekeris waveguide and acoustic source parameters.

在展开截断幂次N = 4时, Pekeris波导中地声参数取区间中值时的距离-传播损失曲线、地声参数区间内随机多项式展开近似传播损失的距离-验证集平均误差曲线分别[30]如图2和图3所示.在传播水平距离10 km以内, 随机多项式展开近似传播损失的误差小于1%; 在趋势上误差仍随着水平传播距离r的增加而增加, 但不再单调, 如图2和图3中圈点部分, 传播损失的部分极大值点位置上近似误差出现极大值.

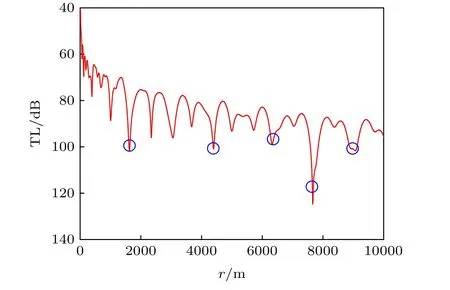
图2 Pekeris波导中100 m深度不同水平距离上的声传播损失, 圈点为传播损失的部分极大值点Fig.2.Acoustic transmission loss at different horizontal ranges with the depth of 100 m in Pekeris waveguide.Circled points are partial local maximum points.

图3 Pekeris波导中100 m深度不同水平距离上随机多项式展开近似声传播损失的验证集误差, 圈点为部分误差极大值点Fig.3.Validation set errors of acoustic transmission loss expanded by polynomial chaos at different horizontal ranges with the depth of 100 m in Pekeris waveguide.Circled points are partial local maximum points.

在计算效率方面, 嵌入随机多项式的声学抛物方程的计算复杂度与算法在深度、水平方向的差分网格数和随机多项式展开截断幂次有关.若声场计算中, 在深度方向上差分离散的网格数为正整数Z, 水平方向上差分离散的网格数为正整数X, 随机多项式展开基个数为Q (对应随机多项式展开截断幂次为 N, Q与N的关系见(2)式), 算法的时间复杂度为

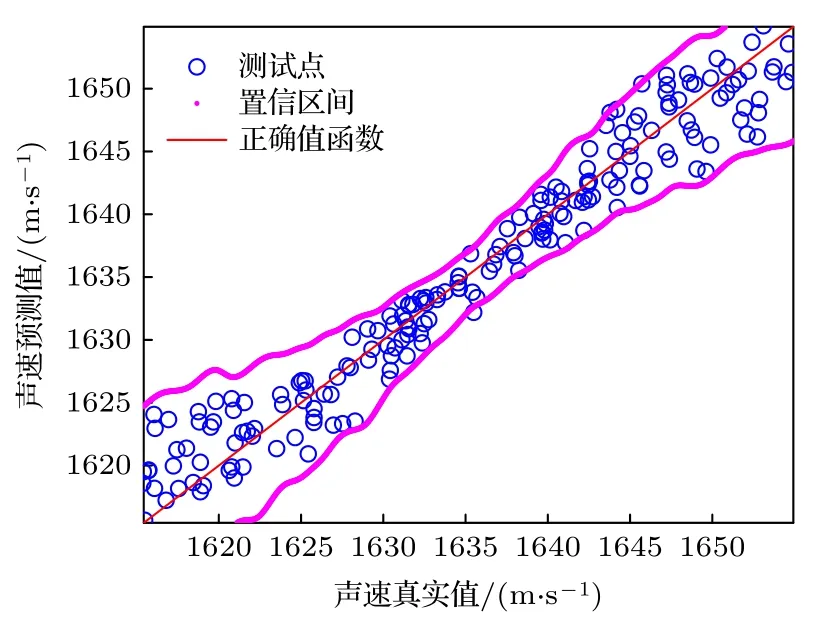
其中参数a正比于截断幂次N, 当 0 ≤N≤10 时,a的变化范围是 1.00

使用基于声学抛物方程的遍历方法, 取海底声速、吸收率、比重取各自搜索区间不同网格点上的数值并计算对应的拷贝声场.方法的计算复杂度与地声参数搜索区间上的网格划分数目有关.假设海底声速、吸收率、比重区间上划分的网格数目相同，记为正整数Y, 基于网格遍历搜索的地声反演算法的计算复杂度为

图4为遍历方案中地声参数的搜索网格数Y取值为50, 随机多项式展开截断幂次N取不同值时遍历搜索法与随机多项式展开法运算复杂度之比随抛物方程算法在深度上的离散网格数Z的变化曲线.可见, 若遍历搜索法的参数搜索网格数Y一定, 随机多项式展开方法的截断幂次N和抛物方程深度方向上的离散网格数 Z 越小时, 随机多项式展开法的计算效率优势越明显.在浅海、低频环境下, 宽角抛物方程声场计算在深度方向上的离散网格数 Z 较小, 随机多项式展开法地声反演的计算效率比遍历搜索法会有极大提升.如在截断幂次N≤6,Z≤6000时, 随机多项式方法相比遍历法的计算效率提高至少一个数量级.

图4 不同随机多项式截断幂次N、不同深度方向差分网格数Z下, 遍历法与随机多项式展开法计算复杂度之比Fig.4.Calculation complexity ratio of the ergodic method and the polynomial chaos expansion method under different polynomial truncated power N and difference grid number in depth direction Z.

4.2 地声反演仿真计算与评估

仿真采用浅海负梯度声速剖面的声传播环境,海水声速剖面如图5所示.声源深度50 m, 采用20—200 Hz频段, 1/3倍频程间隔共计12个中心频点的数据.接收水听器位于海底100 m深度, 收发水平距离为2000—5000 m, 均匀间隔共计61个接收水听器.海底纵波声速、吸收率、比重的搜索区间为

图5 仿真计算使用的海水声速剖面Fig.5.Sound speed profile used in the simulation case.

以嵌入随机多项式的抛物方程模型计算展开系数矩阵, 用简正波模型[32]计算的传播损失作为仿真的实验传播损失, 以此反演海底的声学参数.

考虑实际的实验条件, 声信号的信噪比条件、水文的不确知和水听器位置的误差都会影响反演结果的准确度.仿真验证了在接收信号不同信噪比, 收发水平距离存在不同大小的随机误差时的反演结果.表2和表3为在海底声学参数搜索区间随机取样5000组声速、吸收率、比重作为真实值, 使用随机多项式展开反演结果之误差均值.海底声速、吸收率、比重的反演平均误差随着信噪比的增加近似指数衰减, 随着收发水平距离误差的增加近似指数增加, 在实验中应避免选择信噪比低或收发水平位置存在较大误差(如垂直阵中靠近海表的水听器)的信号作为数据, 以提高反演精度.

表2 接收信号不同信噪比下反演误差均值Table 2.Average inversion errors under different signal to noise ratios.

表3 收发水平距离不同误差下反演误差均值Table 3.Average inversion errors under different horizontal distances.

在信号存在噪声、收发水平距离存在随机误差时, 存在最优的展开幂次 Nb使得反演的误差最小.图6给出了无噪声、收发距离准确, 以及信噪比15 dB、收发距离存在 ± 20 m以内的随机误差时, 反演误差均值与随机多项式截断幂次N的变化.

图6 不同随机多项式展开截断幂次下, (a)海底声速、(b)吸收率、(c)比重反演结果的误差Fig.6.Errors of geo-acoustic inversion results for (a) sound speed, (b) attenuation and (c) ratio of density under different truncated powers of polynomial chaos.

在不考虑信号噪声和收发位置随机因素时, 反演结果随着随机多项式展开截断幂次的增加而愈加准确; 但是噪声和收发水平距离误差使得反演存在最优截断幂次 Nb.

1) 当截断幂次 N

图7 随机多项式展开截断幂次 N =1 时的海底声速的反演结果Fig.7.Geo-acoustic inversion results of sound speed of seabed when the truncated power of polynomial chaos N =1.

2) 当截断幂次 N >Nb时, 随着截断幂次N的增加, 随机多项式展开基的个数快速增加, 系数矩阵的条件数快速增长, 方程(13)的解对传播损失的误差愈加敏感, 反演方法的鲁棒性丧失,使得反演结果不准确.

Nb的选择受到待反演物理量、信噪比、收发水平距离误差大小的影响.仿真算例中, 信噪比15 dB、收发水平距离误差为 ± 20 m时, 海底声速、吸收率、比重的最优截断幂次 Nb分别为 Nb=3,2,3.在反演的区间内随机抽取声速、吸收率、比重的三者测试样本200组, 反演结果与95%置信区间如图8所示.在此条件下, 海底声速、吸收率、比重的反演平均误差为1.34 m/s, 0.02 dB/λ, 0.03.在实际的反演过程中, 为了保证反演结果的可靠性, 可以采用后验方法评估反演的结果, 从采用不同截断幂次的反演结果中挑选出泛化效果最优的结果.

图8 信噪比为15 dB, 收发水平距离误差为 ± 20 m时,(a)模拟声速、(b)吸收率、(c)比重的反演结果及其置信区间Fig.8.Geo-acoustic inversion results and its confidential intervals of (a) sound speed, (b) sound attenuation and (c) ratios of density between seabed and sea water when the signal to noise ratio is 15 dB and error of horizontal distance is ± 20 m.

在反演的计算时间方面, 采用遍历法在海底参数搜索区间网格数Y = 40与采用随机多项式展开法在不同截断幂次N下反演所需要的计算时间如表4所列.在本算例采用的最优截断幂次下, 随机多项式展开法的计算用时在遍历法的1%以内。此外, 仿真发现: 在截断幂次 N ≤6 时, 使用随机多项式展开方法反演地声参数比基于代价函数搜索的遗传算法具有效率优势.

表4 使用遍历法与随机多项式展开法反演海底参数所需计算时间Table 4.Calculation time of geo-acoustic inversion using method of traversing and polynomial chaos expansion.

5 结 论

本文提出一种利用宽带、多收发位置的传播损失和地声参数搜索区间内传播损失的随机多项式展开系数矩阵快速反演海底声速、吸收率、比重的方法。展开系数矩阵由嵌入随机多项式的宽角抛物方程声场计算模型求解获得.根据仿真实验的结果，得到以下主要结论.

1)随机多项式展开法在中低声波频率、一定的声传播水平距离以内、海底参数搜索区间长度适中时, 相较于遍历搜索的地声反演方法, 提高了反演的计算效率: 在深度上的差分网格数小于6000,随机多项式展开截断幂次小于6时, 计算效率至少可以提高一个数量级.在仿真算例中, 使用最优的随机多项式展开截断幂次时, 随机多项式展开法反演地声参数的时间开销不到遍历法的1%.

2)在高信噪比、收发相对位置误差较小时，使用宽带多收发位置传播损失随机多项式展开系数矩阵, 可准确且唯一地反演海底声速、吸收率、比重.仿真算例中: 在信噪比大于15 dB, 收发距离误差小于20 m时, 声速、吸收率、比重的反演误差小于1.34 m/s, 0.02 dB/λ, 0.03.