基于光路补偿的数字全息干涉法测量液相扩散系数
黄子珊,林佳茂,翁佳炫,邓军灿,陈俊旭,彭 力, 2, 3
(1. 华南师范大学 物理与电信工程学院,广东 广州 510006;2. 华南师大(清远)科技创新研究院有限公司,广东 清远 5115173;3. 华南师范大学 物理国家级实验教学示范中心,广东 广州 510006)
液相扩散系数在化工、炼油、生化、制药环保等领域中有着重要的作用[1],如何有效测量液相扩散系数有着重要的意义. 目前,测量扩散系数的方法有膜池法[2]、毛细管法[3]、Taylor分散法[4]与光干涉法[5]等. 但上述方法有操作时间长、精度较低、较难读取数据等不足之处. 由此,本文以光干涉法为基础,应用数字全息技术来测量两种不同溶液间的扩散系数,使用CCD相机对得到的干涉条纹进行记录,并通过Matlab软件对数据进行处理,得到所需的液相扩散系数. 此外,在原有的Mach-Zehnder干涉光路中,本文添加了与扩散槽尺寸材质等完全相同的补偿槽,添加光路补偿后的干涉条纹明暗衬比度显著提高.
1 理论分析
1.1 扩散原理
在各向同性材料中,单位时间内通过垂直于扩散方向的单位截面积的扩散物质(称为扩散通量Diffusion flux,用J表示)与该截面处的浓度梯度(Concentration gradient)成比例,即[1]
(1)
式中C为物质的浓度,z代表扩散方向,D为扩散系数,负号表示扩散方向与浓度梯度方向相反.
本文中的扩散体系高度远大于长宽,扩散可看作仅在竖直方向中进行,即扩散为一维z方向扩散.图1中扩散体系为一个长方体体积元,其边长分别为2dx、2dy、2dz.

图1 扩散体系
设长方体的中心P(x,y,z),该点处的溶质浓度为C,溶质由下表面扩散到体积元的速率为
(2)
溶质由上表面扩散到体积元的速率为
(3)
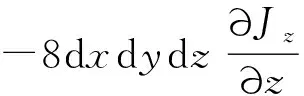
(4)
体积元中扩散溶质的增加速率还可以表示为
(5)
结合式(4)和(5),可得
(6)
将式(1)代入式(6)中可得
(7)
当扩散可看做是一维时,在初始时有较为明显的分界面. Turchiello R F等人求解式(7)后,可得扩散槽中自由扩散的浓度分布为[6]
(8)
其中C1、C2为两个不同溶液的浓度.
1.2 水平条纹判读法
溶液的浓度变化会改变其折射率,进而改变其透射光的光程差(或相位差).在本实验中,物光波的相位差就是由于折射率变化引起的.相位差变化为
(9)
其中L是扩散体系的厚度,λ是激光的波长,而Δn(z,t1,t2)则是在扩散体系z位置t1、t2时刻之间的折射率变化.
在较小的浓度变化范围,折射率可视为线性变化的[7],可得
(10)
其中(dn/dc)0是折射率对浓度的导数,在小浓度变化范围内可以视作常数,n0为常数.
将式(10)代入到式(8)中,折射率之差的分布可以表示为
Δn(z,t1,t2)=
(11)
对式(9)求导并使其等于0,可得到浓度变化的极值点.
(12)
在相位差分布曲线图(如图5)上存在两个极值点,设在z方向坐标分别为zA和zB.
由式(11)和式(12)可得
(13)
由式(13)可推导出液相扩散系数的表达式为
(14)
其中Δz=zA-zB.
在获得不同时刻的干涉图像后,将两幅不同时刻再现的物光波前作点除运算,利用郭盈等人的全息图样处理方法[8]得到浓度变化最大值之间的距离Δz后即可由式(14)计算出液相扩散系数.
1.4 数字全息的实验条件
全息图的光强分布由4个分量所决定,对其做傅里叶变换,可得到全息图的空间频谱为
G(ξ,η)=C1(ξ,η)+C2(ξ,η)+C3(ξ,η)+C4(ξ,η)
(15)
若物光波分布为有限带宽,其最高空间频率为fmax,带宽为2fmax.其中C1是在频谱平面坐标原点上的一个δ函数,C2是物光波频谱分布的自相关函数,带宽扩展到为4fmax,C3和C4分别表示物光波的±1级频谱,其中心分别位于±f0处,带宽为2fmax[1].为了提取物光场,应使C2、C3、C4互相不重叠,即需要满足条件
(16)

θmin=arcsin(3fmaxλ)
(17)
当物参夹角大于θmin时,可以在频谱面上滤掉C2、C3和C4分量,仅将C3提取出来,对该分量进行傅里叶变换,可以重现全息图平面上的物光波前.
物参夹角的确定除了需要满足物光频谱信息分离条件外,干涉条纹间距还需要满足大于CCD的分辨率的条件. 根据奈奎斯特采样定理,为了准确恢复干涉强度分布函数,每一个干涉条纹周期必须大于两个CCD像素周期,即
δx≥2ΔxH,δy≥2ΔyH
(18)
干涉条纹的空间频率由物光和参考光之间夹角决定,最小条纹周期对应的物光夹角为
(19)
其中,δmin为最小条纹周期,θmax为最大物参夹角.
由于物参夹角一般较小,所以sinθ≈θ,由此可得到物参夹角范围为
(20)
综合式(17)和式(20),可以得到数字全息干涉的有效物参夹角需要满足的条件为
(21)
物参夹角存在一个最佳值,在这个物参夹角的情况下,所能记录的物波频谱达到最大.其中fcx=1/(2ΔxH)为所能记录的最大频谱,当f0=3dfcx/4,记录下的物波频谱达到最大,即
(22)
(23)
将实验中CCD照相机尺寸ΔxH=5 μm和λ=520 nm代入上式,得到最佳物光夹角为2.2351°.在实验中,可以通过调节图2中的平面镜角度来调节物参夹角使之达到最佳角度.
2 实验装置
如图2所示,实验装置由左至右分别为520 nm固体激光器、扩束镜、挡光板、反射镜与半透半反镜、扩散槽、补偿槽和工业CCD相机.

图2 实验装置图
液相扩散在扩散槽中进行,槽内下半部分装有锥形整流栅,可减湍流和返混对实验测量的影响,使扩散稳定进行.
为了提高明暗条纹的对比度,实验光路中添加了与扩散槽完全相同的补偿槽. 补偿槽可以补偿光程,使参考光和物光的光强大致相等,从而提高干涉条纹明暗对比度.
将CCD工业相机与计算机相连,将实验获得的干涉条纹导入计算机后,经处理便可得到相应的扩散系数.
3 实验数据处理
本文采用的图像处理方法思路如图3所示.

图3 图像处理方法思路
采集不同时刻的干涉图样,对图样进行小波去噪,滤除噪声的同时保持干涉条纹细节,从信号中提取信息. 经过矩形窗口频域滤波,滤除掉参考光的直透部分、物体各点的自相关以及物体各点之间的互相关项和原始物光波前共轭像的频谱,保留原始物光波前的频谱,将该频谱经过逆傅里叶变换转换到空间域,得到包含扩散进行程度信息的物光波[9].
利用不同时刻的两幅物光波中的相位信息,求得包裹相位差. 对包裹的相位差进行二维解包裹运算后可得连续的相位差. 判读出扩散方向上浓度变化极值点间的垂直距离,代入式(14)后可计算得到质扩散系数值.
4 实验结果与讨论
4.1 25℃时0.1 mol/L蔗糖水溶液扩散系数
使用浓度为0.1 mol/L的蔗糖水溶液作为样品,在25℃下进行实验,利用CCD工业相机得到不同时刻干涉图样. 图4为不同时刻的蔗糖水溶液干涉图样.


图4 不同时刻蔗糖水溶液干涉图样
经过最小二乘解包裹算法后得到连续的相位差(图5),进一步可得到峰-峰值距离Δz.

图5 连续相位差图
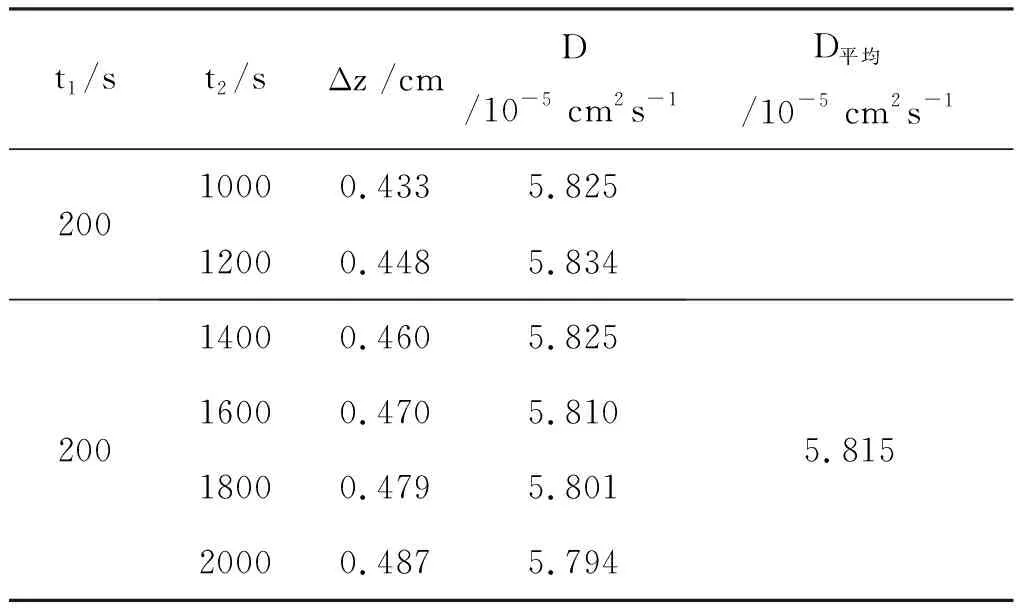
表1 25℃时0.1 mol/L蔗糖水溶液扩散系数
记录多组不同时刻的干涉图样,利用Matlab对每组干涉图样进行图像处理,得到峰峰值距离Δz,再根据式(14)计算出每组干涉图样所对应的扩散系数,实验结果如表1所示,可得扩散系数的平均值为5.815×10-5cm2s-1. 在25℃下0.1 mol/L的蔗糖水溶液扩散系数理论值为5.694×10-5cm2s-1[10],实验所得扩散系数与理论值的百分误差为2.121%.
4.2 光路补偿对于实验的影响
如图6所示,在未加入补偿槽时,干涉图样明暗条纹对比度低,条纹模糊不清. 添加与扩散槽尺寸相同的补偿槽后,实验图像明显清晰了许多.

图6 补偿槽加入与否的干涉图样对比图
在后期数据处理时,明暗条纹衬比度不够会使Matlab识别产生偏差,干涉图样模糊的图像在图像处理后得到的连续相位差图波动较多,更难判别浓度变化极大值点. 光路补偿后的干涉图样衬比度高,提高了图像处理的精度.
分析实验的各个影响因素,实验误差主要来源于以下几个方面:实验时,注液速度过快等会使扩散体系内有湍流产生,浓度变化过大时浓度与折射率关系不再呈线性,实验精度将受到影响;用CCD工业相机采集全息干涉条纹时,人员走动和外界振动等干扰因素会导致干涉条纹图的微弱振动,这将一定程度上影响干涉条纹的质量;室内、外杂光的影响会使条纹的调制度降低,对后续的处理带来影响,降低数字图像处理结果的准确性;空气的温度、湿度和气流的变化都可能会对干涉光路造成影响,从而使得实验精度下降.
4 结束语
本文基于光路补偿的数字全息干涉法测量液相扩散系数,利用生活中易得的低功率激光器,搭建了操作简单、成本低、安全性高的装置. 在对扩散系数进行测量的同时还定性分析了扩散系数测量的影响因素,在接下来的工作中,可以建立数学模型对其进行定量的分析,讨论抖动、注液速度快慢等对于扩散系数测量的影响,从而提高扩散系数的测量精度.

