数学学科育人的几个视角

张金勤 朱宇

教育的根本使命在于“育人”，这是所有学科共同的核心任务。作为基础教育的一门重要学科，小学数学理应体现立德树人导向，寓育人目标于学科教学之中。育人目标不是空谈，要渗透到实实在在的教学实践中，从这个意义上说，课堂是学科育人的主阵地。那么，怎样发挥数学学科特点，发掘育人关键元素，从学科教学走向学科育人，实现教书与育人的和谐统一呢？在此，笔者辑录几位数学名师的教学案例片段，与读者共同分享他们在教学中把握育人契机，让数学学科立德树人功能真正落实的教学智慧。

【片段一】学科知识的视角——系统认知，整体建构

许卫兵（认识面积）

师：怎样计量，才能知道面积的大小呢？

生（齐）：定标准，去测量，得结果。

师：很好。这是计量的步骤，也是测量的方法。今天，我们在学过计量时间、长度、质量的基础上，又学到了一种新的计量——

生（齐）：面积。

师：那你觉得面积和时间一样吗？和长度一样吗？和质量一样吗？

生：都不同。

师：千金难买回头看。计量长度时，用含有刻度的尺子去测量，尺子上的刻度，实际上就是测量用的标准。先定下标准，然后去测量，就能知道实际长度了。这样一比较，你有什么发现吗？

生：每一个时间单位，其实也是标准，用时间标准去测量，最后得到多少时间。

生：计量质量时，我们也先定了质量的标准才能测量，最后得到有多重。

师：面积、长度、质量、时间，它们虽然看起来都不一样，但是在数学上，我们把它们都叫作计量。所以，看起来我们学习了很多内容，实际上——

生：实际上学得很少。

生：它们之间都是相通的、有联系的。

【赏析】《义务教育数学课程标准（2011年版）》指出：“把每堂课教学的知识置于整体知识的体系中，注重知识的结构和体系……”碎片化的零散堆砌不符合数学知识体系严密性和系统性的要求。因此，在教学中，许老师抓住知识点间的纵横联系，帮助学生形成知识结构和认知建构，促进学生思维水平自动化程度的提升。许老师站在系统的、结构的高度，从本课的计量对象——面积，扩展到长度、质量、时间等其他计量对象，以整体关联的视角，启发学生感悟到面积、长度、质量、时间，它们虽然看起来都不一样，但是都经历了“定标准，去测量，得结果”这几个步骤，在深化概念理解的同时，促进了学生原有认知结构的完善与发展。这样的处理，让学生得到了宏观的、结构化的引导，由衷地感受到知识是会“生长”的，主动求知的积极情感被充分激发，课堂由此充满了张力。

【片段二】学科技能的视角——激发兴趣，张扬个性

潘小明（角的度量）

教师出示练习纸，让学生独自尝试测量∠1的度数并做记录。学生在投影仪上演示，量得∠1是30°。

师：有没有量出的度数不是30°的？

生：我量出的是150°。

（许多学生认为错了，该生也发现自己是看反了）

生：我发现好像是31°。

（教师让该学生在投影仪上演示，该学生可能想要证实自己的31°是正确的，将一条边往31°刻度线靠，其他同学纷纷指出下面的边要对齐）

师：还有不同答案吗？有没有32°的？

生：我开始量出的是32°，我想确认一下，再量了一次，发现刚才的一条边没有对齐，应该是30°。

师：刚才这位同学说，他开始量出的是32°，为了确认一下是否正确，他又量了一次，结果量得是30°。那我就不知道到底是第一次的32°对，还是第二次的30°对？

生：第二次的30°是对的。

（教师让学生在投影仪上进行演示）

生：我前面不小心量成了32°，后来我再量时发现没对齐，应该是30°。

师：你说的对齐，是指要对齐哪些东西？

生：先要把这个孔与角的顶点重合。

师：这个孔就是量角器的什么？

生：是量角器的中心。

师：既要将角的顶点与量角器的中心对齐，又要把角的一条边与0刻度线对齐，然后，看另一条边对准的刻度就是这个角的度数。

【赏析】数学学习的价值不仅在于习得学科知识，还在于掌握学科技能。学科技能是发展学生综合能力的重要组成部分。学科技能的掌握，是成就学生个性化发展的必由之路。在教学中，潘老师没有直接带领学生学习量角的方法，而是本着“理解量角器原理”与“掌握量角方法”兼顾的原则，放手让学生独立尝试量角，启发学生反思出现不同答案的原因，自发寻找“对准”“重合”等关键要素，自主归纳量角的步骤和方法。从上述教学片段中，我们不难看出，潘老师精心组织实践操作，秉承“差异性”和“个性化”的育人理念，引导学生充分经历度量工具形成的过程，不断进行对比分析，促进学生对量角本质的理解，为下节课画角技能的习得打下基础。技能训练不能把学生当作亦步亦趋的“操作工”，要追求方法的深刻性、本质化，促进学生思维能力、解决问题能力的实质性提升，培养学生自信、自主、独立的精神品质。

【片段三】数学思想的视角——聚焦本质，着眼长远

周卫东（常见的数量关系）

师：老师开车从苏州到海安，汽车的速度是90千米/小时，时间2小时，路程是多少千米？

生：90×2=180（千米）。

师：感谢你们帮老师算出了苏州到海安的路程是180千米。如果老师开摩托车要几小时？摩托車的速度是60千米/小时。

生：180÷60=3（小时）。

师：如果将来开通了动车要几小时？动车的速度是180千米/小时。

生：180÷180=1（小时）。

师：你们都是怎么求出时间的？

生：路程÷速度=时间。

师：看来根据路程和速度就可以求出时间了。

师：那如果要求速度呢？

生：路程÷时间=速度。

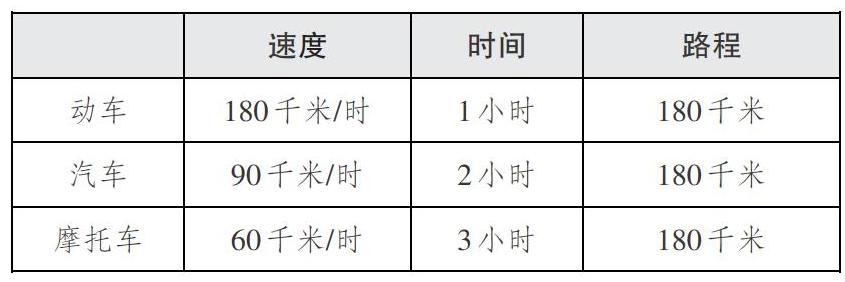
[ 速度 时间 路程 动车 180千米/时 1小时 180千米 汽车 90千米/时 2小时 180千米 摩托车 60千米/时 3小时 180千米 ]

师：观察上面这张表格，你们还有什么发现吗？

生：我发现速度×时间=路程。

生：我发现路程相同，速度不同所用的时间也不同。

生：路程不变，速度越快，时间越少。

师：随着交通工具的发展，速度越来越快，所需时间越来越短，但这三者之间的关系有没有发生变化？

生：没有。

师：都是路程=速度×时间。

【赏析】“常见的数量关系”是苏教版数学教材四年级下册第三单元“三位数乘两位数”中的重要内容，是学生进一步学习正、反比例函数的重要基本模型。教学中，周老师为学生提供丰富的感性材料，培养学生的数学思维，不断丰富学生对“路程、时间和速度”三者之间关系的感知，在此基础上通过理性的思考抽象出三个量之间的关系的模型。在层层深入的对话中，创设了路程不变、时间随着速度的变化而变化的教学情境，含而不露地进行了函数思想的启蒙，其价值已经超越了知识的理解与模型的建构。抽象思想是数学的基本思想之一，学生从量或形的视角，认识、分析客观事物，抽象出某种数学模型，这个过程与人类认识客观世界的过程完全一致，教学中，周老师让学生经历了知识的“再创造”过程，在促进学生对数量关系理解的同时，抽象、函数思想等数学素养的培育也落到了实处。

【片段四】数学文化的视角——培根固本，丰厚底蕴

蔡宏圣（用字母表示数）

师：下面一个练习是“编故事”，故事的主角是a×4。老师先做个示范。如果a表示一本数学书的重量，那么a×4就是？

生（齐）：4本数学书的重量。

师：而且是4本同样的数学书的重量。下面，哪个同学来编？

（学生用a代表各种数量，说了a×4的意思）

师：既然大家把a×4讲得这样丰富多彩，老师就讲个这方面的历史故事。

（学生鼓掌）

师：在历史上，对于数量和数量之间的关系，我们人类最初是用文字表示的。

（课件出示：单个重量×4，单个价钱×4，每班人数×4。其中“重”“价”“人”用红色标出）

师：这样表示比较烦琐。后来，古希腊数学家丢番图想到了用缩写的方法来表示。这里的“单个重量×4”，取“重”发音的第一个字母，表示成“z×4”。那么“单个价钱×4”和“每班人数×4”怎样用缩写的方法表示？

生：j×4和r×4。

师：丢番图用字母的缩写来表示数量间的关系，虽然简洁了，但每个字母都表示特定的意思，不能把z×4和j×4混同起来，所以，并没有给数学家研究数学带来更多的简便。到16世纪，法国数学家韦达想，如果把各种情境中字母表示的特定意思都去掉的话，不都是一个数和4相乘吗？

（课件中的“z×4”“j×4”“r×4”依次变为“□×4”）

师：所以，韦达就表示成了a×4，这里的a还是特定的意思吗？

生（齐）：不是！

师：对，字母a已经不表示任何具体的意义，和这里的小方块一样，只是一个符号而已。（板书：符号）自从韦达把字母当作符号来表示数之后，许多数学难题得到了解决，数学获得了飞速发展，韦达被称为现代代数学之父。

师（稍做停顿）：从丢番图用缩写的方法表示数到韦达把字母当作符号来表示数，用了整整1200年！

（学生情不自禁地发出了惊呼）

师：同学们，我们只用了40分钟就跨过了人类认识提升的1200年历史，你们的表现是最棒的。

【赏析】无数的教育实践告诉我们，学科文化之于育人，就如同“一方水土养育一方人”，通过学科文化的路径来培育学生，实质就是“育其根”。教学中，蔡老师放手让学生“编故事”，充分体验“用字母表示数”的概括性，还原从“具体对象”到“字母式子”的抽象过程。在此基础上，水到渠成地呈现从丢番图到数学家们1200多年所走过的抽象表示数的历程。特别是“我们只用了40分钟就跨过了人类认识提升的1200年历史”激发了学生的学习热情，让他们感受到数学的神奇魅力。层层递进的精彩演绎，学生感受到的不是枯燥无味的历史记录，而是洋溢着探索精神、彰显着人类智慧的不平凡的历程。此时的学生，收获的不仅仅是“用字母表示数”的知识，更有对数学这一学科的价值认同，对数学精神、数学美的深切感受，数学学科文化素养得到了提升。

以上几位名师的教学片段告诉我们，在数学学习的全过程中育人，要以促进学生发展為旨归，将数学的思想和思维方法、数学的精神和品质、数学的文化和价值，潜移默化地落实到数学学习活动的各个层面，促进学生生动活泼、全面而有个性的成长。

（作者单位：江苏省高邮市实验小学 江苏省高邮市天山小学）