去中心基于属性Σ 协议的一般性构造及其应用

杨晓莉，黄振杰

1.闽南师范大学 福建省粒计算及其应用重点实验室，福建 漳州363000

2.闽南师范大学 计算机学院，福建 漳州363000

基于属性密码是密码学的研究热点之一，能通过属性和关于属性的访问结构实现细粒度的访问控制，而且具有很好的隐私性，因此有极广泛的应用场景，其主要内容包括基于属性加密[1]（attribute-based encryption）、基于属性签名[2]（attribute-based signatures）和基于属性身份识别[3]（attribute-based identification）等。基于属性密码的研究成果丰富且持续不断，2020 年仍有不少研究成果报道，比如Dong 等[4]基于格提出一个服务器辅助可撤销基于属性加密方案，Ishizaka等[5]给出一个从可搜索加密到基于属性加密的一般性构造，Cui 等[6]给出一个密钥可再生的基于属性加密方案，Ali等[7]给出一个基于属性层次加密方案，Deng 等[8]给出一个基于属性代理重加密方案，Le等[9]的基于属性加密的密文压缩，Takashima[10]提出一个表达力强且密文长度固定的基于属性加密方案，Zhao等[11]研究了基于属性加密的黑盒和公开可追踪性，Okamoto等[12]的去中心基于属性加密和签名。

在最初的基于属性密码系统中，用户密钥是由单个属性权威中心颁发的，如果这个权威中心腐败了，那么整个系统就没安全性可言了，这是一个严重的缺点。另外，单个属性权威中心也容易出现瓶颈问题。为满足大规模分布式应用的需求，学者们提出了多权威（multi-authority）基于属性加密[13]、多权威基于属性签名[14]和去中心（decentralized）基于属性加密[15]、去中心基于属性签名[16]。多权威基于属性密码系统虽然是由多个属性机构来分发密钥，但仍然有一个特殊中心权威机构，由它给各属性权威机构分发密钥。这个特殊中心权威机构仍然身系整个系统的安全性，因此，多权威基于属性密码虽然解决了瓶颈问题，但仍未解决安全性问题。去中心基于属性密码系统中不存在任何特殊的中心机构，系统中的各个属性机构相互独立。一个机构的腐败只影响其管理的属性，不构成整个系统的安全性灾难。去中心基于属性密码最大程度解决传统基于属性密码的两大缺点。

零知识证明（zero-knowledge proof）是Goldwasser等[17]于1985 年提出的重要密码原语，同时具备两个看起来相互矛盾的性质：一方面，要使验证者接受某个声明；另一方面，要让验证者不能从证明过程中得到任何知识。Σ 协议是一种三轮公开抛硬币诚实验证者零知识交互证明协议，是由Cramer等[18-19]首先定义的。Σ 协议的一个重要应用是通过Fiat-Shamir转换得到数字签名方案，重要的Σ 协议和对应的签名方案有：Schnorr[20]和Beth[21]的基于离散对数的协议和签名方案；Ong等[22]的基于大整数分解的协议和签名方案；Guillou 等[23]、Shamir[24]、Okamoto[25]和Girault[26]的基于RSA困难性的协议和签名方案；Hess[27]和Cha等[28]的基于Computational Diffie-Hellman 困难性的协议和签名方案。

虽然基于属性密码和Σ 协议都受到密码学学者的广泛注意，但到目前还没有基于属性Σ 协议的研究报道。目前已有一些相近的概念，但都与基于属性Σ 协议有重要的区别。

相近的概念有：

（1）Cramer 等[18]的部分知识证明（proofs of partial knowledge）和Anada 等[29]的谓词知识证明（proofs of predicates knowledge）本质上是相同的，都是一种证据不可区分证明协议，可以用来证明拥有满足访问结构的某个证据集，而且在证明过程中到底是使用哪个证据集是不可区分的。这两个性质与基于属性Σ 协议是相同的，但它们都不考虑共谋攻击问题，即不要求用来证明的证据集是属于同一个人的，也就是说，证据集是可以“凑”的；而在基于属性Σ 协议中，证据必须是同一个用户的，这就是基于属性Σ 协议的抗共谋性。

（2）Anada等[3,29]的基于属性身份识别（ABI）通过证明拥有满足访问结构的某个属性集私钥来证明身份，而且也考虑了抗共谋性。它与基于属性Σ 协议的区别在于安全性要求不同：基于属性身份识别主要是要求抗假扮（against impersonation），不考虑零知识性；而基于属性Σ 协议要求具有特殊鲁棒性（special soundness）和诚实验证者零知识性（honestverifier zero-knowledge）。一般来说，基于属性Σ 协议可以用作基于属性身份识别方案，反之则不一定可以。比如文献[3]的基于属性身份识别方案就不是零知识证明协议，更不可能是Σ 协议。

（3）Anada等[30]研究的匿名身份验证（anonymous authentication）与基于属性身份识别有点相近，具有匿名性，能抗错误验证（against misauthentication），但这里的匿名性是指不知道用户到底是使用哪个密钥，对应的属性集却是明确的，这与基于属性密码的隐私性是有明显不同的。基于属性密码的隐私性要求对应的属性集是隐藏的、不可知的。另一方面，为了减少计算量，匿名身份验证也不要求抗共谋。因此，匿名身份验证在隐私性和抗共谋性方面都弱于基于属性Σ 协议。

本文将基于属性密码引入到知识证明领域，研究基于属性Σ 协议。作为直接的应用场景，基于属性Σ 协议可以为各种信息系统提供匿名认证服务。与现有匿名认证机制相比，基于属性Σ 协议具有访问控制表达能力强、粒度细的优点。本文所提出的方案是去中心的，解决了单个机构的瓶颈问题和系统的安全性问题，因此应用场景更加广阔。基于属性Σ协议作为一种新的密码学原语是十分值得研究的，不仅能进一步丰富基于属性密码和知识证明这两个密码学重要领域的内容，还能通过其重要应用而间接丰富数字签名、匿名认证、匿名访问控制等其他领域。

本文的主要贡献有：

（1）提出基于属性Σ 协议的概念，给出（去中心）基于属性Σ 协议的定义和安全模型。

（2）基于标准Σ 协议、陷门可取样关系和平滑秘密共享方案，提出一个去中心基于属性Σ 协议的一般性构造方法，并证明方案的安全性。因为已有丰富的标准Σ 协议[20-28]，所以由本文方法可以得到一系列去中心基于属性Σ 协议。

（3）作为去中心基于属性Σ 协议的应用，利用Fiat-Shamir转换，得到一个去中心基于属性签名和一个去中心基于属性双层签名的一般性构造方法。同样地，由此可以得到一系列去中心基于属性签名和去中心基于属性双层签名方案。

（4）效率分析表明，本文的去中心基于属性签名和去中心基于属性双层签名方案相比已有的方案在数据长度和计算开销两方面都具有显著的优势。而且本文的方案是去中心的，克服了瓶颈问题和系统安全性依赖单个中心的问题。

1 预备知识

1.1 平滑秘密共享方案

秘密共享方案可以将一个秘密值s的份额分发给n个参与者，每个参与者得到一个份额，使得一些参与者可以使用他们所拥有的份额重构出秘密值s。能够重构出秘密值的参与者子集称为许可集。秘密共享方案称为完善的，如果任何非许可集都不能获得关于秘密值s的任何信息。

如下Shamir(t,n)门限方案是一个常用的完善秘密共享方案，可以将域F中的秘密值s分拆成n个份额，使得任意t个互不相同的份额可以重构出秘密值s。

Shamir(t,n)门限方案：

（1）分拆方法：随机选取常数项为s的t-1 次多项式f(x)∈F(x)，随机选取xi∈F，i∈{1,2,…,n}，计算n个份额f(xi)。

（2）重构方法：已知t个互不相同的份额j∈{1,2,…,t}，构造Lagrange插值公式：

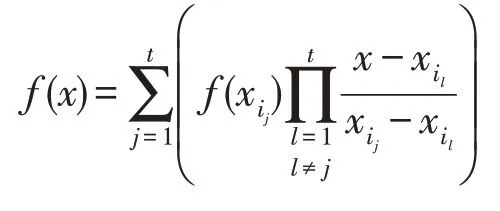
计算秘密值s=f(0)。

所有许可集构成的集合称为秘密共享方案的访问结构Γ。一个访问结构Γ称为单调的，如果A是一个许可集，那么任何包含A的集合也是许可集。

设Γ是总体N上定义的访问结构。对任意A⊆N，记为A在N中的补集。定义Γ的对偶访问结构Γ∗如下：

例如，上述(t,n)门限的对偶是(n-t+1,n)门限。

定义1一个完善的秘密共享方案称为半平滑的（semi-smooth），如果满足下面（1）～（4）；如果还满足（5），则称为平滑的（smooth）。

（1）方案生成的所有份额都是多项式长的。

（2）秘密的分发和重构都可在多项式时间内完成。

（3）给定秘密及其全部份额，可以在多项式时间内检验它们是正确的。

（4）给定任何秘密值，由任何非许可集的份额都可以在多项式时间内扩充成完整份额。

（5）对于任意非许可集，其成员的份额都是互相独立的。

上述Shamir(t,n)门限方案就是平滑的。

1.2 标准Σ 协议

知识证明是这样的一种协议，通过它证明者P可以向验证者V 证明其知道指定声明x所对应的证据w。所有的声明x和相应证据w构成一个二元关系R={(x,w)}。

定义2标准Σ 协议是一种3 轮公开抛硬币诚实验证者零知识交互证明协议，由Σgen、Σcom、Σcha、Σres、Σvrf、Σext、Σsim7个算法组成。

（1）Σgen:输入系统安全参数1k，输出公开参数pp和一个二元关系R={(x,w)}。

（2）Σcom:由证明者P 执行，输入一对声明和证据(x,w)，输出承诺COM和状态St，并发送承诺COM给验证者V。

（3）Σcha:由验证者V 执行，输入承诺COM和声明x，公开抛硬币随机选择一个挑战CHA发送给P。

（4）Σres:由证明者P 执行，输入声明x，证据w，承诺COM，状态St和挑战CHA，输出一个响应RES，并发送给验证者V。

（5）Σvrf:由验证者V 执行，输入声明x，承诺COM，挑战CHA和响应RES，输出一个决定值d。d=1表示接受本次证明；d=0 表示不接受。

（6）Σext:是证据提取器，输入相同声明x的两个会话副本，提取证据w′。

（7）Σsim:是仿真器，输入声明x，输出一个仿真副本(COM∗,CHA∗,RES∗)。

在执行一次证明协议过程中，双方交互的所有消息所构成的集合称为一个会话副本。能让验证算法输出1的副本称为可接受副本。

Σ 协议应具有正确性、特殊鲁棒性和诚实验证者零知识性：

正确性（completeness）：对于任何的(x,w)∈R，如果(COM,CHA,RES)是正确执行协议所产生的副本，那么它是可接受副本。即

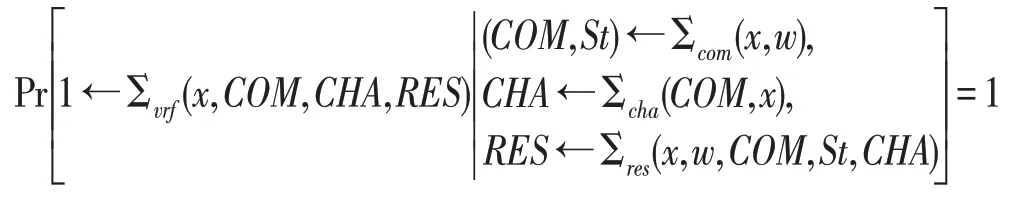
特殊鲁棒性（special soundness）：如果存在一个知识提取器Σext，从对应于相同声明x的两个可接受副本(COM,CHA,RES)和(COM,CHA′,RES′)（其中承诺COM相同，挑战CHA、CHA′不同），能以压倒性概率μ提取出x的一个证据w′，则称Σ 协议具有特殊鲁棒性。即

诚实验证者零知识性（honest-verifier zeroknowledge）：如果存在一个仿真器Σsim能产生与真实副本不可区分的仿真副本(COM∗,CHA∗,RES∗)，则称Σ 协议具有诚实验证者零知识性。即，对于任意的多项式时间区别器D，都有：

分别为真实副本和仿真副本分布，ε为可忽略量。这里假定验证者V是诚实的，它总是诚实运行Σcha来产生挑战值。

由Σ 协议的上述3个性质可知，它也具有如下证据不可区分性。文献[18]中的Σ 协议也是证据不可区分的。

证据不可区分（witness indistinguishable）：对于任意的验证者V、任意的声明x及其任意的两个证据w1和w2，分别使用证据w1和w2进行证明所得的两个副本是不可区分的。即，对于任意的多项式时间区别器D，都有：

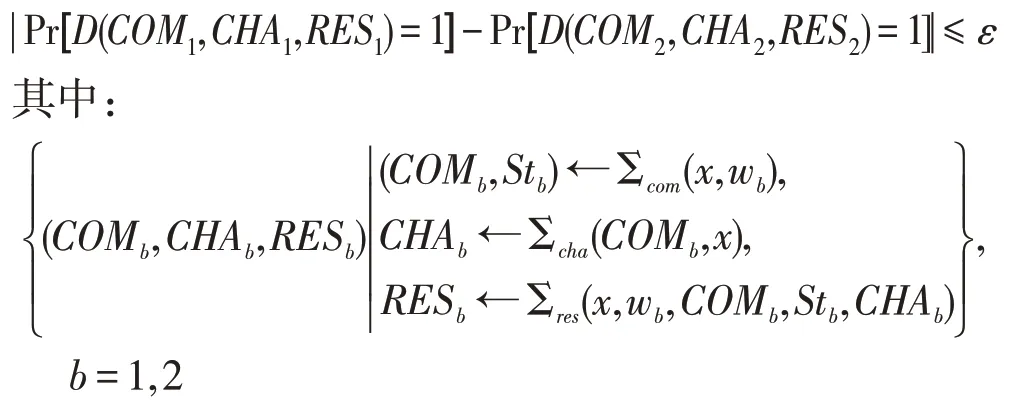
如下Beth方案[21]是一个常用的Σ 协议。

Beth-Σ 协议：

①选择大素数q阶乘法群G及其生成元g，记=(G,q,g)；

②随机选取r∈Zq，计算R=gr；

③随机选取x∈Zq，计算X=gx；

④随机选取h∈Zq，计算s=r-1(h-Rx) modq；

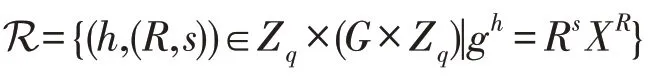
1.3 陷门可取样关系

对于关系R，定义值域Rng(R)={y:∃x,(x,y)∈R}，x的像集R(x)={y:(x,y)∈R}，y的原像集R-1(y)={x:(x,y)∈R}。

定义3一个陷门可取样关系（trapdoor samplable relations，TSR）由满足正则性和求逆困难性的三个算法(TDG,Smp,Inv)组成，记为∏TSR(TDG,Smp,Inv)。

（1）生成算法TDG：输入安全参数1k；输出公开参数pp，关系R的描述和陷门t。

（2）取样算法Smp：输入关系R 的描述；输出在关系R上均匀分布的(x,y)。

（3）求逆算法Inv：输入关系R的描述，对应的陷门t和元素y∈Rng(R)；输出y的一个随机原像x。

（4）正则性:对于由TDG产生的任意一个关系R，存在一个正整数d，使得对所有的y∈Rng(R)，都有|R-1(y)|=d。

陷门可取样关系实例：

（1）TDG(1k)：

①选择大素数q阶乘法群G及其生成元g，记=(G,q,g)；

②随机选取陷门x∈Zq，计算X=gx；

上述陷门可取样关系是q-正则的，其求逆困难性相当于求离散对数困难性。

2 去中心基于属性Σ 协议

2.1 去中心基于属性Σ 协议的定义

在定义基于属性Σ 协议之前，先定义一种特殊的关系，称之为基于属性关系。

假设系统属性总体为N，Γ为N上的访问结构，基于属性关系定义为：

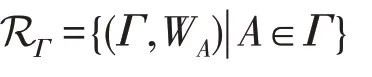
其中，WA为“拥有属性集A∈Γ”的同用户同次证据。

一般来说，系统会在不同时候为不同用户对相同或不同属性集A生成不同的证据。在关系RΓ中，要求证据WA是为同一个用户生成的关于属性集A的同一次证据，目的是防止共谋攻击，即防止用A1的证据和A2的证据凑成作为A1⋃A2的证据。假设用户1拥有属性子集A1，用户2拥有属性子集A2，A1和A2都不满足访问结构Γ，但A1⋃A2可能满足访问结构Γ；或者，用户原来拥有属性子集A1，后来由于身份变化而变更为拥有属性子集A2，有可能A1和A2都不满足访问结构Γ，但A1⋃A2满足访问结构Γ。如果不要求是同用户同次证据，恶意用户就可能欺骗验证者。

称关于上述基于属性关系RΓ的具有属性隐私性的Σ 协议为基于属性Σ 协议。下面给出去中心基于属性Σ 协议的准确定义。

为方便叙述，假设系统有n个属性机构，每个属性机构管理1 个属性，即总属性集N={1,2,…,n}，属性机构i管理属性i。

在去中心系统中，每个属性机构是独立为用户生成对应证据的，为了防止上述的共谋攻击，让各自独立的属性机构能协同生成一致性的同用户同次证据，在下面的定义及一般性方案中都引入证据标识τ。具有相同证据标识τ的证据才能一起使用，用来防止敌手从不同属性机构处“凑”证据来欺骗验证者。

定义4一个去中心基于属性Σ 协议由如下算法组 成，记 为

2.2 安全性定义

基于属性Σ 协议除必须具有一般Σ 协议的正确性、特殊鲁棒性和诚实验证者零知识性外，还须具有属性隐私性。

正确性：对于任何的(Γ,Wτ,A)∈RΓ，如果(COM,CHA,RES)是正确执行协议所产生的副本，那么它是可接受副本。即

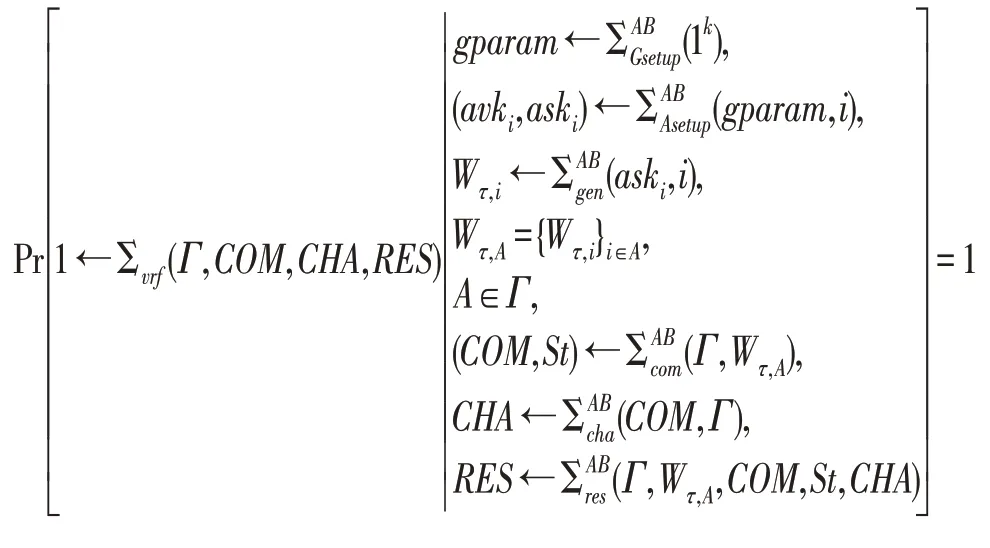
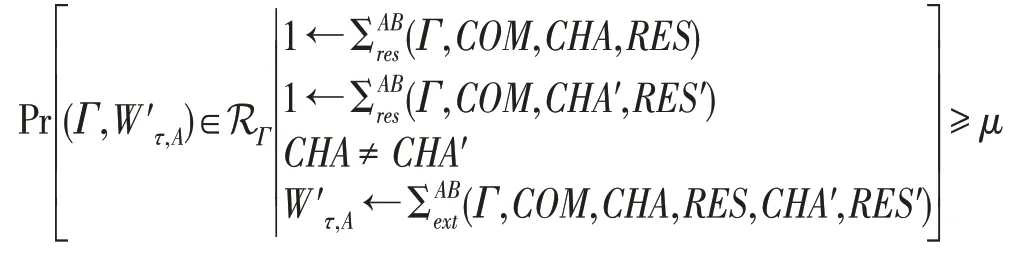
注：上述定义要求有相同证据标识τ是防止共谋攻击的关键，如果对于不同证据标识的副本也能提取证据，那么就会存在共谋攻击。

分别为真实副本和仿真副本分布，ε为可忽略量。这里假定验证者V是诚实的，它总是诚实运行来产生挑战值。

属性隐私性（attribute-privacy）：对于任意的访问结构Γ和任意两个属性集A,A′∈Γ，用证据Wτ,A和Wτ,A′进行证明，所产生的副本(COM,CHA,RES) 和(COM′,CHA′,RES′)是不可区分的。即对于任意的多项式时间区别器D，都有：

3 去中心基于属性Σ 协议的一般性构造

本章利用标准Σ 协议、陷门可取样关系和平滑秘密共享方案来构造去中心基于属性Σ 协议，并证明其安全性。

3.1 一般性构造方案

条件1如下两个分布相同：

条件2仿真器是从挑战空间随机选取挑战CHA∗的。

条件3的挑战空间与Ψ的份额空间相同。

满足这样条件的标准Σ 协议是普通存在的，比如引言中提到的文献[20-28]所提出的方案都满足条件。

②选取Hash函数H:{0,1}∗→Rng(R)；

③输出全局参数gparam=pp。

①计算xi=H(i||τ),wi←Invi(xi,ti)；

②输出Wτ,i=wi。

①计算xi=H(i||τ),i∈N；

②(COMi,Sti)←

③(COMi,CHAi,RESi)←

④输出承诺COM={COMi}i∈N；

⑤状态St={{Sti}i∈A,{CHAi,RESi}i∈Aˉ}。

①将份额{CHAi|i∈Aˉ}扩充成CHA关于Γ∗的完整份额，记扩充得到的份额为{CHAi|i∈A}；

②RESi←

③输出响应RES={(CHAi,RESi)}i∈N。

①计算xi=H(i||τ),i∈N；

②如果有某个i∈N则输出0；

③如果{CHAi|i∈N}不是CHA关于Γ∗的完整份额，则输出0；

④输出1。

①记A={i|CHAi≠CHA′i,i∈N}；

②wi←i∈A；

③输出{wi}i∈A。

①随机选取A∈Γ；

②从挑战空间随机选取挑战CHA∗和

注：基于属性Σ 协议的作用是让证明者可以向验证者证明其拥有满足访问结构的属性，因此双方都必须知道证明所指向的访问结构，把访问结构作为的输入。但其运行时只需要知道挑战空间，不需要输入访问结构Γ、承诺COM和标识τ，这是因为Σ 协议的挑战是随机选取的。把它们作为输入只是为了方便验证阶段找准对应的数据。

3.2 一个实例

使用1.2 节的Beth-∑协议，1.3 节的陷门可取样关系实例和1.1节的Shamir(t,n)门限方案，由上述的一般性方法，可以得到如下去中心基于属性Σ 协议。证明者可向验证者证明其拥有系统n个属性中的t个。为方便叙述，不妨假设证明者拥有前t个证据。记为

①选择大素数q阶乘法群G及其生成元g，记

②选取Hash函数H:{0,1}∗→Zq；

③输出全局参数gparam=

①随机选取xi∈Zq，计算；

②输出该机构的公私钥avki=Xi，aski=xi。

①随机选取ri∈Zq，计算，hi=H(i||Ri||τ)，

②输出证据Wτ,i={Ri,si}和标识τ。

①对每个i∈{1,2,…,t}，随机选取yi∈Zq，计算承诺

②对每个i∈{t+1,t+2,…,n}，随机选取ci,zi∈Zq，Ri∈G，计算

③计算hi=H(i||Ri||τ),i∈{1,2,…,n}；

①用(0,c),(t+1,ct+1),…,(i,ci),…,(n,cn),i∈{t+1,t+2,…,n}这n-t+1 个点构造n-t次拉格朗日插值多项式Pn-t(x)；

②计算ci=Pn-t(i),i∈{1,2,…,t}；

③计算zi=yi+cisimodq,i∈{1,2,…,t}；

①用(0,c),(t+1,ct+1),…,(i,ci),…,(n,cn),i∈{t+1,t+2,…,n}重构n-t次拉格朗日插值多项式Pn-t(x)；

②验证是否有ci=Pn-t(i),i∈{1,2,…,t}；

③计算hi=H(i||Ri||τ),i∈{1,2,…,n}；

⑤如果以上都成立，则输出1；否则输出0。

①记A={i|ci≠c′i,i∈{1,2,…,n}}；

②si=(ci-c′i)-1(zi-z′i) modq,i∈A；

③输出{si}i∈A。

②随机选取n-t次多项式Pn-t(x)，记其常数项为c∗；

3.3 安全性证明

本节证明上述构造的协议是去中心基于属性Σ协议，即具有正确性、特殊鲁棒性、诚实验证者零知识性和属性隐私性。

定理1如果所使用的标准Σ 协议、陷门可取样关系和平滑秘密共享方案是正确的，且满足3个条件，那么上述构造的去中心基于属性Σ 协议是正确的。

证明因为∏TSR(TDG,Smp,Inv)是陷门可取样关系，且Smp的输出与的输出同分布（条件1），所以算法产生的(xi,wi)可以作为的声明与证据。条件3保证算法中的扩展份额可以进行。

对于任意属性集A，当i∈A时，COMi是由产生的，CHAi是产生的CHA在Γ∗下的份额，RESi是由(COMi,Sti,CHAi,wi)产生的，因此只要是正确的，那么一定能有(COMi,CHAi,RESi)=1。当i∈Aˉ时，(COMi,CHAi,RESi)是由(H(i||τ))产生的，只要是正确的，自然也有RESi)=1。

注意到，在方案中{CHAi|i∈N}本来就是CHA关于Γ∗的完整份额，因此只要是正确的，就是正确的。

定理2如果所使用的标准Σ 协议具有特殊鲁棒性且秘密共享方案是半平滑的，那么上述构造的去中心基于属性Σ 协议具有特殊鲁棒性。

证明假设(COM,CHA,RES)和(COM,CHA′,RES′)是对应于声明Γ的相同证据标识τ的两个可接受副本，且CHA≠CHA′，只需要证明提取器能提取出满足访问结构Γ的证据{wi}i∈A。

令A={i|CHAi≠CHA′i,i∈N}，因为是对于每个i∈A调用来提取wi的，所以由的特殊鲁棒性可知能提取出{wi}i∈A，而且所有证据{wi}i∈A都对应于同一个标识τ。

接下来证明A∈Γ。否则，如果A∉Γ，那么就有。注意到={i|CHAi=CHA′i,i∈N}，而且CHAi和CHA′i分别是CHA和CHA′关于Γ∗的完整份额，则有CHA=CHA′，与假设矛盾。

总之，{wi}i∈A是声明Γ的一个合格证据，上述构造的去中心基于属性Σ 协议方案具有特殊鲁棒性。

定理3如果所使用的标准Σ 协议具有诚实验证者零知识性，且满足条件2，那么上述构造的去中心基于属性Σ 协议具有诚实验证者零知识性。

证明条件2 保证方案的仿真器能正确运行。仿真器就是对每个i∈N使用，只要输出的副本是不可区分的，那么输出的副本就也是不可区分的。因此，只要具有诚实验证者零知识性，那么就具有诚实验证者零知识性。

定理4如果所使用的基础Σ 协议是证据不可区分的，秘密共享方案是平滑的，那么上述构造的去中心基于属性Σ 协议具有属性隐私性。

证明首先，因为基础Σ 协议是证据不可区分的（文献[18]），所以{COMi|i∈N}，只与yi=H(i||τ)有关，与所使用的属性集无关。

最后，因为{RESi|i∈N}由{COMi,CHAi|i∈N}完全决定，所以也与所使用的属性集无关。

总之，整个副本{(COMi,CHAi,RESi)}i∈N与所使用的属性集无关，属性隐私性成立。

4 去中心基于属性Σ 协议的应用

4.1 去中心基于属性签名

使用著名的Fiat-Shamir 转换可以将上述去中心基于属性Σ 协议转换成去中心基于属性签名，得到如下方案，记为∏ABS(Gsetup,Asetup,Gen,Sign,Vrf)。

（1）Gsetup(1k)：同3.1 节的，但增加一个从{0,1}*到挑战空间的Hash函数H1。

（2）Asetup：同3.1节的

（3）Gen(aski,i,τ)：同3.1 节的，只是这里把输出的wi称为关于属性i私钥skτ,i，属性集A的私钥skA={skτ,i}i∈A。

（4）Sign(skA,m,Γ)：输入私钥skA={skτ,i}i∈A，消息m和访问结构Γ。

①令Wτ,A={wi}i∈A={skτ,i}i∈A=skA；

②{COM,St}←

③计算CHA=H1(COM||Γ||τ||m)；

④RES←

⑤输出签名σ=(τ,COM,CHA,RES)。

（5）Vrf(m,Γ,σ)：输入消息m，访问结构Γ和签名σ。

①计算CHA=H1(COM||Γ||τ||m)；

②b←

③如果b=1，则签名σ有效，否则无效。

将上述一般性方法用于3.2 节的方案，可以得到一个新的去中心基于属性签名方案，其签名算法如下，算法（1）～（3）和（5）基本上和3.2节方案的对应算法一样。

去中心基于属性签名方案：

（1）Gsetup(1k)：同3.2节的

（2）Asetup：同3.2节的

（3）Gen(aski,i,τ)：同3.2 节的，只是这里把输出的wi称为关于属性i私钥skτ,i，属性集A的私钥skA={skτ,i}i∈A。

（4）Sign(skA,m,Γ)：输入私钥，标识τ和消息m。

①对每个i∈{1,2,…,t}，随机选取yi∈Zq，计算

②对每个i∈{t+1,t+2,…,n}，随机选取ci,zi∈Zq，Ri∈G，计算

③计算hi=H(i||Ri||τ),i∈{1,2,…,n}；

④计算c=H(R1||R2||…||Rn||Y1||Y2||…||Yn||m)；

⑤用(0,c),(t+1,ct+1),…,(i,ci),…,(n,cn),i∈{t+1,t+2,…,n}这n-t+1 个点构造n-t次拉格朗日插值多项式Pn-t(x)；

⑥计算ci=Pn-t(i),i∈{1,2,…,t}；

⑦计算zi=yi+cisimodq,i∈{1,2,…,t}；

⑧输出签名σ=

（5）Vrf(m,Γ,σ)：同3.2 节的，只是这里c=H(R1||R2||…||Rn||Y1||Y2||…||Yn||m)。

Fiat-Shamir转换保证签名方案的不可伪造性，只要Σ 协议具有特殊鲁棒性。去中心基于属性签名方案的属性隐私性直接从去中心基于属性Σ 协议继承。

4.2 基于属性的双层签名

双层签名（tow-tier signature）[31]是Bellare和Shoup在PKC2007提出的，签名方案中用户有两个密钥，第一个称为一层密钥，用来计算第二层密钥；二层密钥是一次性签名密钥，用来对消息进行签名，但每个二层签名密钥都只签一个消息，每个消息都换新的密钥来签。这样做的好处是可以提高安全性，达到标准模型下的可证明安全性。2016 年Anada 等[32]研究了基于属性双层签名（attribute-based two-tier signatures），给出正式定义和一个方案。

用Fiat-Shamir 转换也可以将3.1 节的一般性方案转换成基于属性双层签名方案。上节本文转换出基于属性签名的一般方案，本节直接转换出基于属性双层签名的具体方案，得到首个去中心基于属性双层签名方案。下面方案的访问结构是(t,n)门限，为叙述方便，假设用户拥有前t个属性。记为∏ABTTS(Gsetup,Asetup,PKGen,Sign,Vrf)。

（1）Gsetup(1k)：生成全局公共参数。

①选择大素数q阶乘法群G及其生成元g，记

②选取Hash函数H:{0,1}∗→Zq；

（2）Asetup(N)：由属性机构i运行，生成属性机构i的公私钥。

①随机选取xi∈Zq，计算

②输出该机构的公私钥avki=Xi，aski=xi。

（3）PKGen({avki,aski},i,τ)：输入机构i的公私钥(Xi,xi)和证据标识τ，生成第一层私钥。

①随机选取ri∈Zq，计算，hi=H(i||Ri||τ)，

②输出用户第一层私钥{Ri,si}。

注：拥有属性集A的用户从相关的属性机构处获得用同标识τ生产的第一层私钥{Ri,si}，构成其第一层私钥

（4）SKGen({avki,aski}i∈A,SKτ,A)：输入属性机构的公钥，用户的第一层私钥，生成第二层公私钥。

①对每个i∈{1,2,…,t}，随机选取yi∈Zq，计算

②对每个i∈{t+1,t+2,…,n}，随机选取ci,zi∈Zq，Ri∈G，计算

③计算hi=H(i||Ri||τ),i∈{1,2,…,n}；

（5）Sign({avki}i∈A,SPKτ,A,SSKτ,A,m,Γ) ：输入第二层公私钥对(SPKτ,A,SSKτ,A)和消息m。

①计算c=H(SPKτ,A||τ||m)；

②用(0,c),(t+1,ct+1),…,(i,ci),…,(n,cn),i∈{t+1,t+2,…,n}这n-t+1 个点构造n-t次拉格朗日插值多项式Pn-t(x)；

③计算ci=Pn-t(i),i∈{1,2,…,t}；

④计算zi=yi+cisimodq,i∈{1,2,…,t}；

（6）Vrf({avki}i∈A,SPKτ,A,σ,m,Γ)：输入机构的公钥，二层公钥SPKτ,A，消息m和签名σ。

①计算c=H(SPKτ,A||τ||m)；

②用(0,c),(t+1,ct+1),…,(i,ci),…,(n,cn),i∈{t+1,t+2,…,n}重构n-t次拉格朗日插值多项式Pn-t(x)；

③验证是否有ci=Pn-t(i),i∈{1,2,…,t}；

④计算hi=H(i||Ri||τ),i∈{1,2,…,n}；

⑥如果以上都成立，则输出1；否则输出0。

同样地，由Fiat-Shamir 转换可以保证上述签名方案的所有安全性。3.2节、4.1节的例子与上面例子的安全性都基于离散对数困难性假设。

4.3 效率比较

基于属性签名方案已有很多，其中大部分是需要双线性对运算的，本文在4.1节给出的一般性方法可产生许多去中心基于属性签名方案，可以是有双线性对运算的方案，也可以是无双线性对运算的方案。一般来说，无对的方案效率会比较高，将本文的方案与现有的无对运算的基于属性签名方案进行比较。因为文献[33-34]的方案都是门限的，所以本文的方案和文献[35]的方案也选择门限结构来比较，结果见表1。在表1和表2中，n是属性总数，t是签名者的属性个数，l是用户数的上限，k为离散对数问题的安全参数，λ为RSA问题的安全参数。RSA模N的长度为2λ，因此当k=160 时就可以达到λ=512 的安全强度。用E和E'分别表示数据规模为160 bit和1 024 bit的一次幂指数运算，tE 就表示计算t次幂指数运算。用DL 表示离散对数困难假设，RSA 表示RSA 假设，SRSA表示强RSA假设（strong RSA assumption）。

从表1 可以看出，本文的方案和文献[35]的方案在各项指标上是相当的，只在签名私钥上本文的方案少1k。这两个方案在除密钥生成开销外的所有指标上都是最优的，而且优势非常显著。在密钥生成开销方面，最优的是文献[33]方案，但这个方案在其他指标方面都是最差的。

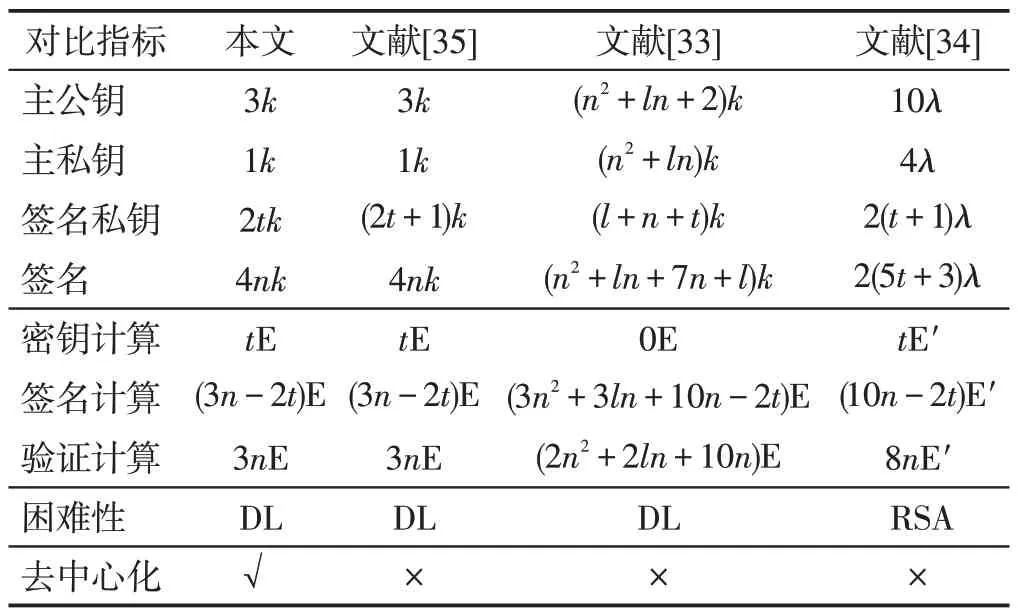
Table 1 Comparison of ABS scheme performance efficiency表1 ABS方案性能效率对比

目前已有的基于属性双层签名方案只有文献[32]的方案，因此将本文4.2节的方案与文献[32]的方案进行效率比较，结果见表2。仍然以访问结构为(t,n)门限作为例子来进行比较。

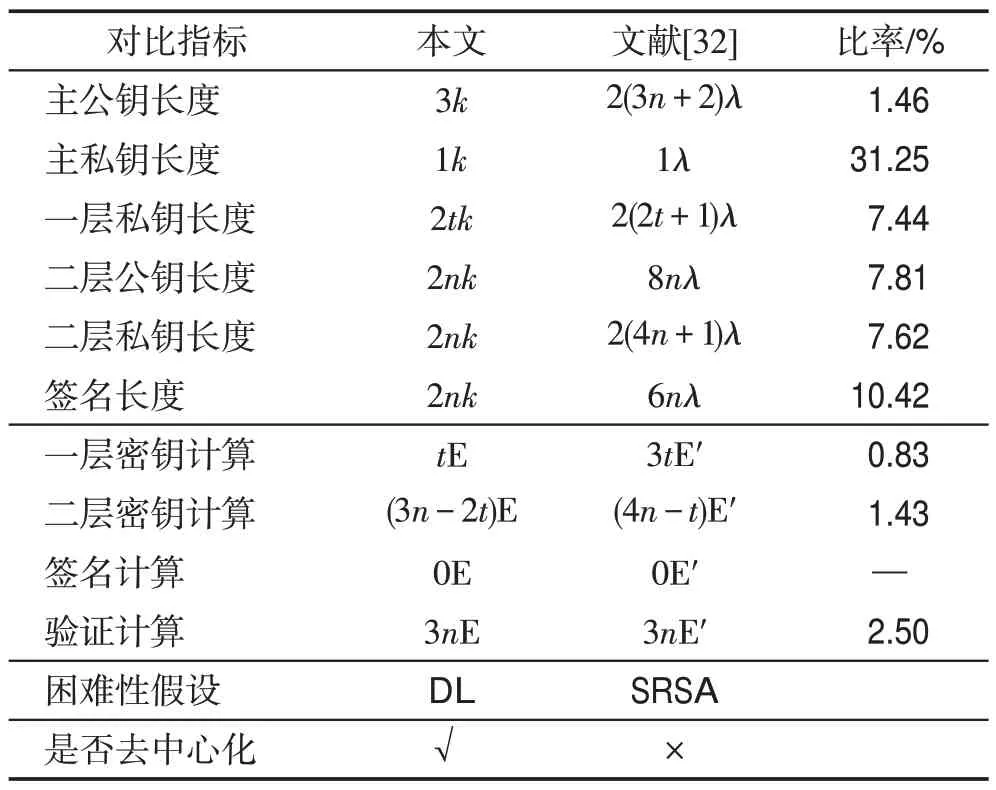
Table 2 Comparison of ABTTS scheme performance efficiency表2 ABTTS方案性能效率对比

为了更直观地比较，用n=10,t=n/2,k=60,λ=1 024 计算了本文方案各项长度和计算开销与文献[32]方案相应值的比率。虽然E和E'都是一次幂指数运算，但由于数据规模差别很大，计算开销也差别很大。在本文方案中，E 是160 bit 规模的幂指数运算，而在文献[32]方案中则是1 024 bit，数据长度相差6.4倍，计算开销至少相差40 倍（长度倍数的平方）。在表2中，按40倍进行估算。

从表2可以看出，对于除签名计算之外的所有指标，本文方案都大大优于文献[32]的方案。两个方案的签名计算都主要是数的相乘、相加和求逆，由于数据规模的原因，本文方案也是有很大优势的。

表2 中，主公钥和主私钥是与文献[32]方案一样按有中心的来计算的，如果按去中心的来计算，每个属性机构都需要各1k长的属性机构公钥和私钥度，因此系统机构公钥总长度为(n′+2)k，机构私钥总长度为n′k，其中n′为属性机构的个数，其最大值是n。按取最大值n′=n来计算，主公钥长度的比率为5.86%，主私钥长度的比率为312.50%。除了主公钥和主私钥的长度之外，其他指标不受是否去中心的影响。也就是说，做到了去中心，本文方案仍然在除主私钥和签名计算之外的指标上具有绝对的优势。因为在去中心系统中，每个属性机构一定要有自己的私钥，所以私钥总数是肯定要增加的，但如果就每个属性机构来说，其私钥长度仍然只有1k，仍然只是文献[32]方案的31.25%。

综上所述，本文方案在数据长度、计算开销和去中心化等方面都具有显著优势。

5 结束语

基于属性密码和Σ 协议都是密码学的重要研究对象，本文将基于属性引入到知识证明领域，研究基于属性Σ 协议，给出其定义，刻画其安全模型。去中心化可以提高基于属性密码系统的抗攻击能力，解决有中心系统的瓶颈问题，本文基于标准Σ 协议、陷门可取样关系和平滑秘密共享方案，给出一个去中心基于属性Σ 协议的一般性构造，并证明其安全性；作为去中心基于属性Σ 协议的应用，利用Fiat-Shamir转换，得到去中心基于属性签名和去中心基于属性双层签名的一般性构造和相应的例子。本文方案要求访问结构是平滑秘密共享方案，提出更一般访问结构的基于属性Σ 协议是未来进一步研究的目标。