结合降噪和自注意力的深度聚类算法
陈俊芬,张 明,赵佳成,谢博鋆,李 艳
1.河北大学 数学与信息科学学院 河北省机器学习与计算智能重点实验室,河北 保定071002
2.北京师范大学珠海分校 应用数学学院,广东 珠海519087
聚类是把无标签数据划分为若干个不相交的类簇,挖掘出有价值的特征和类别信息[1-2]。深度聚类是指基于深度学习技术的聚类方法。相较于传统聚类方法,深度聚类利用网络结构自动学习输入数据的潜在特征,并通过最小化聚类损失函数调整网络参数来达到最优的聚类指派。
自编码器(auto-encoder,AE)是近年来一种经典的无监督学习的非线性特征提取方法[3-5]。自编码器拥有对称结构能进行特征维度约简,其瓶颈层输出可以学习到高维输入数据的低维紧凑的特征表示[6-7]。早期的深度聚类工作是分开执行特征提取与聚类分析[8-9]。特征提取和聚类划分任务依顺序进行,两者耦合度低,学到的特征表示不一定带来好的聚类划分。为了克服这一不足之处,堆叠自编码器的深度嵌入式聚类模型DEC(unsupervised deep embedding for clustering analysis)用联合学习策略来学习特征表示和类标分配[10]。通过不断迭代优化KL损失函数调整模型参数和K-means 的聚类结果。这种联合训练能捕捉适合聚类的特征表示,提高了聚类性能。但当图像的质量下降(噪声、姿态、表情、光照、背景等因素造成),特征映射空间会出现较大偏差,在类边界处的出错率很高,说明特征表示的可分性不够。视觉注意力机制最大化有限的注意力,从局部获得有价值的信息,抑制无用信息。Zheng等人[11]将自注意力加入CNN(convolutional neural network),更好地完成了图像细粒度的识别任务,用更加全局的信息来弥补小卷积核获取信息不足的缺陷。同时,Fu 和Zheng 等人[12]提出了一个全新的循环注意力卷积神经网络,通过由粗到细迭代地生成区域注意力完成纹理细密的物体识别学习。受此启发,将自注意力机制引入深度聚类模型,加强对输入图像的某个局部信息的关注。
为了进一步提高深度聚类模型对复杂图像数据的聚类性能,本文提出了一种新的聚类算法DDC(deep denoising clustering)。DDC聚类方法主要思想包括:采用深度卷积降噪自编码器[13]学习输入数据的特征表示;通过自注意力机制弱化数据的无用信息捕获关键特征;联合训练卷积降噪编码器与K-means聚类算法的统一模型;同时完成特征表示学习和聚类划分两个任务。自注意力机制的本质是对输入数据的各个特征赋予不同的权重来突出更重要的信息,使模型获得更准确的特征表示。本文的主要贡献点为:
(1)提出一种新的深度聚类模型,由卷积降噪自编码器结合自注意力机制组成。
(2)引入一个超参数,放大数据点到非近邻类中心距离来降低其相似性。加快具有唯一最大值的概率向量收敛到one-hot向量的速度。
(3)增加深度聚类模型的多样性,扩大了图像聚类的应用范围。
1 相关工作
1986 年Rumelhart 等人首次提出自编码器概念,主要用于数据压缩[14]。2006 年Hinton 等人[15]用逐层训练好的堆叠自编码器网络参数值作为深度信念网络(deep belief network,DBN)的参数初始值,并用BP(back propagation)算法成功训练了DBN得到很好的分类性能。这种预训练极大地改善了陷入局部极小的情况,由此产生了深度自编码器。2008 年Vincent等人[13]提出降噪自编码器网络(denoising auto-encoder,DAE),通过对噪声数据重构得到干净数据的方式获取更鲁棒的特征表达。堆叠降噪自编码器(stacked denoising auto-encoder,SDA)需要层级训练,过程比较麻烦。为此,Chen等人提出了marginalized SDA[16],其核心思想是随机噪声对图片的损坏利用期望的乘积表示,从而得到了优美的闭形式解,而且算法简单,实验验证效果还不错。2011 年Masci 等人[3]提出卷积自编码器用来捕获图像数据的空间结构信息,进而得到了更好的特征表示。
Tian 等人[8]通过堆叠自编码器学习原图像的非线性特征表示,然后K-means对特征表示执行聚类获得了出色的聚类结果。这类深度聚类算法分为特征学习和聚类划分两部分,前一部分不一定学习到最适合后一部分(聚类划分)的特征表示,从而影响了聚类性能。
近几年,很多新型的深度聚类算法采用联合训练策略去统一学习特征表示和类标分配[17-18]。联合训练策略充分利用聚类结果来调整网络参数。Xie 等人[10]提出一种深度嵌入式聚类算法DEC。该算法使用降噪编码器逐层预训练方式初始化堆叠自编码器,然后优化Kullback-Leibler 散度损失微调该聚类模型。4 个图像数据集上的实验对比显示采用联合训练的DEC 比分部训练的DEC 提供了更出色的聚类性能,验证了联合训练的有效性。接着,Li 等人[19]提出了基于卷积自编码器的深度聚类算法(discriminatively boosted clustering,DBC)。该算法的优势:(1)卷积操作能保留图像的空间局部性[20];(2)判别式增强分配能提高聚类分配的纯度;(3)直接端到端预训练替代层层预训练来初始化卷积自编码器。DBC在MNIST 上聚类精度达到0.964,大大超过DEC 的0.843。Dizaji 等人[21]提出了深度嵌入正则聚类模型(deep clustering via joint convolutional auto-encoder embedding and relative entropy minimization,DEPICT)。该模型使用端到端模式训练卷积降噪编码器,得到初始化的特征表示;使用多项逻辑回归函数(即Softmax 函数)计算特征点与聚类中心点的相似性;编码器的重构损失正则约束KL 散度避免深度聚类模型过拟合。DEPICT 在MNIST 数据集上的聚类精度达到了0.965,目前是最高记录。Yang 等人[22]提出一个基于循环网络的深度聚类框架(joint unsupervised learning of deep representations and image clusters,JULE),该模型将卷积自编码器与agglomerative层次聚类联合训练,获得强大的特征表示和更精确的图像聚类结果。然而,JULE需要微调大量参数,对真实聚类问题并不现实。
尽管这些研究工作从不同方面对联合模型的统一训练进行了研究、优化并取得很好的进展,但仍存在一些不足之处。当图像数据被噪声损坏时,特征映射空间也会出现偏差,这将导致聚类效果大打折扣。为了提高对噪声数据的聚类鲁棒性,本文提出了一种新的深度聚类模型,它可以更好地将被污染的数据映射到特征空间并准确地完成聚类划分。
2 基于卷积降噪编码器的深度聚类算法
图像、视频等高维数据的复杂性体现在:(1)特征内容通常包含一些扰乱信息,影响类簇的划分;(2)体量大,人工选择特征会耗费大量的财力和物力。经典堆叠自编码器的特征表示能力有限,需要加入卷积模块来提高局部特征的表示能力,同时有从噪声数据中提取特征的表示能力,因此本文建立卷积降噪自编码器模型来学习输入数据的最优特征表示。具体地,用深度卷积降噪自编码器和自注意力的深度聚类模型DDC(如图1)来提高K-means的聚类性能。
图1模型的上半部分是卷积降噪编码器;下半部分由编码器网络和聚类算法组成。DDC深度聚类问题描述为:原始图像数据是X=[x1,x2,…,xN],带高斯噪声的图像数据为,每个xi和都代表一幅图片;特征空间的特征嵌入为Z=[z1,z2,…,zN],zi∈Rn,其中N为图片个数,n是特征空间中的特征维度。由原始空间到特征空间的映射为ƒθ:Χ→Ζ,其中θ是网络参数的集合,聚类的类中心为U=[u1,u2,…,uK],其中K是类簇的个数。深度聚类的最后输出是最优的特征表示和类中心以及每个图像的硬指派类标。训练DDC模型包含下面两部分:
(1)用端到端策略训练深度卷积降噪自编码器(deep convolutional denoising auto-encoder,CDAE),见图1 的上半部分,得到网络参数和图像的特征表示;并对当前的特征表示进行K-means 聚类,得到类中心点和聚类划分的硬指派。
(2)用联合策略训练编码器和K-means聚类组成的统一模型DDC(图1的下半部分),优化聚类损失函数来更新网络参数和聚类结果。
2.1 DDC的网络结构
卷积自编码器的网络结构示意图是图1 的上半部分。有4组卷积层和池化层交替连接,会有自注意力层随机加在某个卷积层后面,最后有1个卷积层用来压扁特征图为特征向量,还有1个全连接层组合局部特征。

Fig.1 Framework of DDC algorithm图1 DDC算法的框架示意图
被污染的图像数据指的是混入高斯噪声的原始图像,作为该卷积编码器的输入,输出设置为原始图像,引导网络学习输入数据的鲁棒特征。文献[12]的自注意力机制如图2所示,其中函数f(x)、g(x)和h(x)都是1×1卷积核,但它们的输出通道数会有不同。自注意力的计算过程[12]简单描述为:(1)图像特征分别经过卷积操作转换为3 个特征空间。(2)将f(x)的输出特征转置与g(x)的输出特征相乘,得到各个元素点之间的相关性得分矩阵。(3)利用Softmax 对相关性得分转换成所有元素权重之和为1的概率分布,突出重要元素的权重。(4)将权重系数分布和h(x)输出特征逐元素点相乘,得到自适应的注意力特征。
搭建好具有自注意力和降噪学习的深度卷积降噪编码器结构。随后训练该网络,即最小化目标函数式(1),得到图1上半部分的网络参数值。
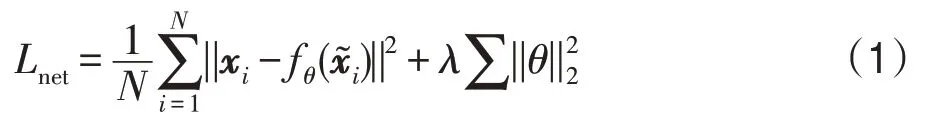
其中,第一部分是降噪卷积编码网络的重构误差;第二部分是网络参数的正则项,可以降低网络过拟合的风险,超参数λ>0。
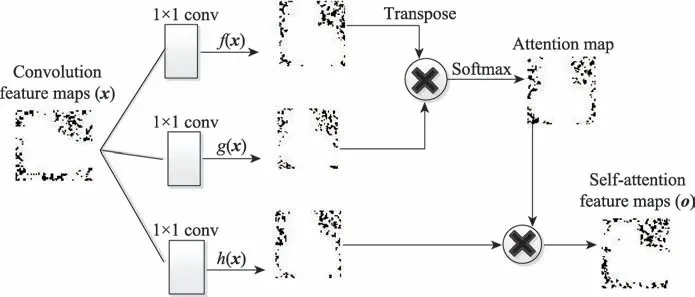
Fig.2 Self-attention mechanism图2 自注意力机制
该深度卷积降噪自编码器将带噪声的图像数据由高维原始空间映射到低维特征空间,得到特征表示。K-means算法对当前得到的特征表示执行聚类,得到类中心点和每个图像数据所属的类别。这也是实验3.6 节中提到的分部训练的CDAE-Kmeans 聚类算法。至此完成了DDC算法的参数初始化。
2.2 DDC的自学习算法
首先计算嵌入点zi与类中心点μj的相似性并归一化为概率值,作为归类的软指派,计算公式为:

由式(2)和式(3)得到两个概率分布向量qi=[qi1,qi2,…,qiK]T和pi=[pi1,pi2,…,piK]T,它们有下列关系:
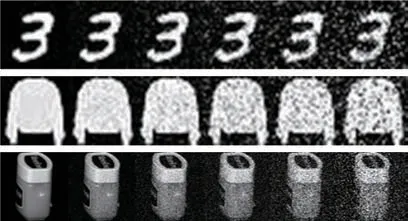
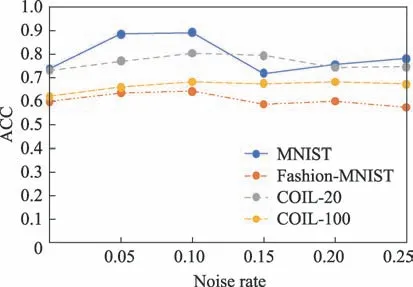
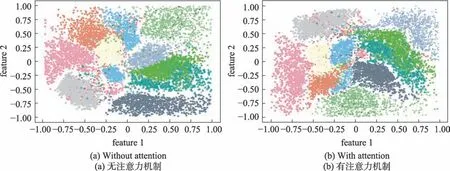
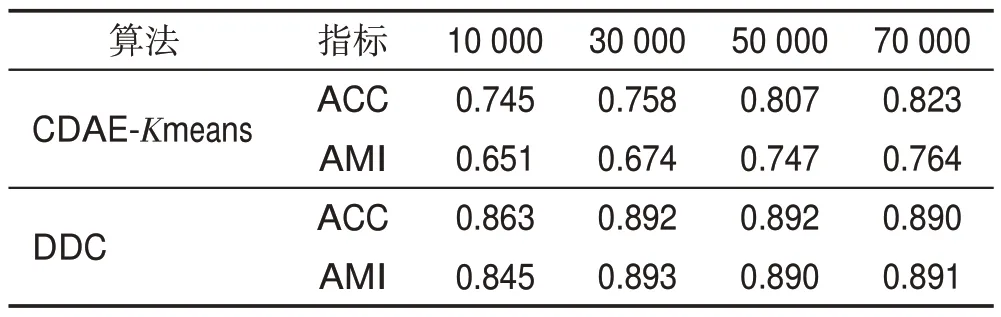
如果有qic=arg max{qi1,qi2,…,qiK}>,则一定有pic>qic且pij 该结论说明辅助目标提高了聚类划分的清晰度。当样本点xi属于类μc,辅助概率pic比聚类概率qic要高,同时降低了属于其他类μj的概率,详细证明过程可见文献[19]。 深度聚类DDC算法的目标函数是所有图像的真实归类的概率分布与目标概率分布的差异性之和,还有网络参数θ的L2约束防止DDC模型过拟合。 计算目标函数Lc对嵌入点zi与类中心点μj的偏导数,得到下面的式(5)和式(6): 根据式(5)用反向传播来更新网络权重和用式(6)更新类中心点,重复该过程直到满足收敛条件。基于深度卷积降噪自编码器与K-means 联合训练的聚类算法,DDC伪代码描述在算法1和算法2中。 算法1CDAE-Kmeans 聚类算法(初始化DDC算法) 输入:图像数据集、类簇个数。 输出:网络权值、特征表示;类中心和聚类指派。 1.预处理 对该数据集进行归一化处理 加入高斯噪声 用高斯分布的随机数初始化网络参数 2.使用端到端策略训练CDAE 对目标函数(1)用随机梯度下降的算法最小化迭代直到收敛 3.输出网络参数值和瓶颈层的特征表示 4.K-means算法对特征进行聚类,得到聚类中心和聚类指派 算法2DDC聚类算法 输入:编码器的参数值和特征表示。 输出:类标向量和类簇中心。 联合训练过程 1.根据式(2)计算真实的概率分布 2.根据式(3)生成辅助概率分布 3.根据式(5)和式(6)迭代更新网络参数和聚类中心,直到满足停止条件 4.对每一个特征表示,按欧式距离找到最近聚类中心点,并将其归入此类簇 算法1(BP 算法训练卷积降噪编码器CDAE)的时间复杂度需要考虑前馈和反向传播两阶段,每一阶段又主要包括卷积层和全连接层的复杂度分析。对一个训练样例,循环一次的算法复杂度为: (1)信息前传过程中卷积层的时间复杂度是O(CinCoutK2M2),其中Cin是输入通道数;Cout是输出通道数;K是卷积核的尺寸;M=是输出特征图的尺寸,由输入尺寸I、卷积核尺寸K、边缘填充p(padding)、步长s(stride)决定。反向传播时的时间复杂度是O(CoutCinK2I2)。 (2)前传过程中全连接层的时间复杂度为O(n1n2),其中n1是输入神经元个数,n2是输出神经元个数。误差反向过程中时间复杂度和前馈计算相同,也是O(n1n2)。 (3)空间复杂度包括卷积层的O(CinCoutK2)和全连接层的O(n1n2)。 算法2 的复杂度主要是K-means 算法的复杂度,其时间复杂度为O(tmNk),空间复杂度为O(N),其中N是样例个数,k是聚类个数,tm是算法循环次数。 本章在4 个真实图像数据集上验证所提算法的聚类性能,并与经典深度聚类算法进行比较。实验环境:硬件平台为Intel®CoreTMi5-4590处理器,8.0 GB RAM;编程环境为Anaconda5.3.1,使用开源的深度学习框架Keras库搭建DDC网络。 MNIST 是10 个手写数字的图像集,包含70 000张28×28 的灰度图片。Fashion-MNIST是10类日常穿着的数据集,也包含70 000张28×28 的灰度图片。COIL-20 包含20 类常见的生活物品,每类物品有72张128×128 不同角度的灰度图片,共1 440 张图片。而COIL-100包含100类物品的128×128 不同角度的7 200个彩色图片。4个图像数据集的部分图片展示在图3中。 Fig.3 Several examples of 4 image datasets图3 4个图像数据集的部分样例 已知图像数据X和真实划分U={U1,U2,…,UR},某一聚类算法提供的聚类结果为V={V1,V2,…,VC}。本文的评价指标包括聚类结果可视化、聚类精度(clustering accuracy,ACC)和调整互信息系数(adjusted mutual information,AMI)[23-24]。 聚类精度ACC 是聚类正确的数据数N1与总数N的比值,即: 指标AMI 利用基于互信息来衡量聚类结果,计算公式如下: 其中,H(U)和H(V)是U和V的信息熵,MI(U,V)是互信息,E[MI(U,V)]是互信息的期望。聚类精度和调整互信息这两个评价指标的数值越接近1,说明聚类结果越可靠,准确度越高。 深度聚类算法DDC在这4个数据集上的网络参数列于表1。表1中,Conv和Pool列中的第一个数字代表卷积核个数,第二部分代表卷积核尺寸,而“—”表示该部分不存在。MNIST上Conv1后有一个自注意力层;Fashion-MNIST 和COIL-100 的Conv2 后各有一个自注意力层;而COIL-20上Conv4后有一个自注意力层。自注意力机制的本质是对各个特征赋予不同的权重使模型获得更准确的特征表示,因此本文网络模型中卷积层后随机加入1个自注意力层。 首先,用正态分布Ν(0,0.012)生成的随机数初始化权重。所有层的激活函数是ReLU函数,卷积核都是5×5 且步长为1,除了COIL-20 上的Conv5 是4×4。全部用2×2 的最大池化,且每个池化层后有一个正则化层,这能缓解梯度消失并规范权重。每个batchsize是256。 Table 1 Detailed network structure settings表1 详细的网络结构设置 其次,联合训练阶段采用Adam 优化器[25]。相比于随机梯度下降优化器(stochastic gradient descent,SGD)[26],Adam优化器能更快收敛且最终聚类性能较SGD好。 最后,为了减少随机初始化类中心点对K-means聚类性能的影响,后面实验提供的K-means聚类结果均是重复50次实验中最好的结果。 首先,一组实验在带噪声的数据集上进行,来验证深度卷积降噪编码器从噪声数据学习特征表示的有效性。人工混入高斯噪声,噪声比例范围是0~25%,图4 展示了加入不同高斯噪声比的3 个图像。经典K-means 聚类算法对所提取的特征数据进行聚类。DDC 算法在这3个带噪声的数据集上的聚类性能指标画在图5、图6中,注意此组实验加入了注意力机制。 Fig.4 Examples from COIL-20 dataset with different proportional Gaussian noises图4 COIL-20数据集上不同高斯噪声比的样例 Fig.5 ACC with varying noise rates on 4 datasets图5 在4个数据集上变化噪声比的聚类精度 Fig.6 AMI with varying noise rates on 4 datasets图6 在4个数据集上变化噪声比的标准互信息 由图5和图6可以看出,在干净数据上DDC算法的聚类精度和互信息不是最高。当噪声比例由0 变到10%,聚类精度逐步提升,说明卷积降噪编码器能捕捉到有效的特征表示。当噪声比超过10%,图像受损比较严重,导致该编码器的重构偏差比较大,特征表示能力又下降,因此聚类精度有所下降。在嵌入了10%噪声的数据上,聚类精度和互信息都达到了最好。验证了深度卷积降噪编码器能从噪声数据中学到更鲁棒的特征表示,提升了K-means 的聚类性能。在后面的实验中,DDC 均采用含10%高斯噪声的数据执行聚类分析。 第二组实验在4个数据集上验证DDC算法对注意力机制的有效性。K-means 算法对这组特征表示的聚类性能列于表2。相应地,随机选取部分聚类结果可视化在图7~图10。 Table 2 Influence of self-attention mechanism used in DDC algorithm on clustering performances表2 DDC算法中自注意力机制对聚类结果的影响 由表2可以看出,注意力机制较大幅度地提升了DDC算法在COIL-20数据集上的聚类性能;在Fashion-MNIST数据集上有小幅度的提升;而在MNIST数据集上没变化。由此可见,注意力机制有助于卷积编码器学习适合聚类的特征表示,为正确聚类划分提供有力保障。 Fig.7 Clustering results of DDC algorithm on MNIST图7 DDC算法在MNIST上的部分聚类结果 Fig.8 Clustering results of DDC algorithm on Fashion-MNIST图8 DDC算法在Fashion-MNIST上的部分聚类结果 从图7可以看出,DDC算法提供了不错的聚类结果。但是DDC算法对同一类簇的某些“异形个体”不能正确归类,比如带钩的数字9、带横的数字1和物品的侧面等。当某些个体和类簇内的主体差别较大时,如何对它们正确归类是下一步要研究的问题。 Fig.9 Clustering results of DDC algorithm on COIL-20图9 DDC算法在COIL-20上的部分聚类结果 Fig.10 Clustering results of DDC algorithm on COIL-100图10 DDC算法在COIL-100上的部分聚类结果 观察图8~图10 可以看到,DDC 算法在Fashion-MNIST 上的聚类性能稍弱;COIL-20 中存在少量“侧视图”,DDC 难以辨识这些有稍大旋转角度的图像,例如标号2 的物体被错误地划分为15 和13;COIL-100的某些类簇之间相似性很大,比如汽车之间主要存在颜色差异,DDC算法未能识别这种差异,聚类结果不是很好。 另外,深度卷积降噪编码器在MNIST 数据集上学习到二维特征展示在图11 中。图11(a)是未引入注意力学到的二维特征,而图11(b)是引入注意力学到的二维特征。若类簇间具有清晰的边界则表明卷积编码器性能优异,学到的特征表示有益于正确归类。可以看到图11(a)的团簇分布交叠较混乱,边界模糊且某两个数字均被分为不相关的区域里;而图11(b)的类簇比较集中,边界比较清晰,每个数字基本上都有自己的区域。可见,结合了自注意力的卷积降噪编码器更能捕获手写数字的关键细节特征,摒弃无用信息,能更好地完成特征学习任务。 本组实验包括DDC和CDAE-Kmeans算法在4个数据集上的深度聚类,聚类性能指标见表3。CDAEKmeans算法是先学习特征表示,然后K-means聚类。DEC[10]和K-means算法对干净图像聚类。 在MNIST 数据集上,K-means 的聚类性能最差,聚类精度仅仅达到0.392。用端到端联合训练的DEC 算法提供了0.841 的聚类精度。同样用端到端联合训练的DDC 算法有0.892 的聚类精度。用端到端分部训练的CDAE-Kmeans的性能优于K-means却比DEC 和DDC 差。这组实验证实了特征表示对提升聚类性能的重要性;联合训练比分部训练提取到更有利于聚类的特征表示;拥有降噪和注意力的DDC算法优于其他3个算法。 Fashion-MNIST 数据集上的结果与MNIST 上的结果类似,K-means的聚类性能最差,而DDC最好,但DEC 的性能比CDAE-Kmeans 稍差。这是由于DEC算法采用堆叠编码器提取特征,而CDAE-Kmeans 用卷积降噪自编码器提取特征。卷积网络的优势是其特征中保留着近邻关系和空间局部性。 在COIL-20 数据集上,DEC 算法的聚类性能低于K-means,而CDAE-Kmeans 和DDC 的聚类性能都优于DEC。观察COIL-20 的图像可知:很多物品的轮廓大致对称,并且多张图片有旋转角度。DEC 算法学到的特征表示不能辨识出较大角度的图片,而CDAE-Kmeans和DDC算法表现比较好,能学到一些有辨识力的特征表示,从而出色地完成聚类划分。 在COIL-100上,DEC算法的聚类性能与K-means相当,CDAE-Kmeans和DDC均优于DEC。由于COIL-100 的类别数比COIL-20 多,物体有较大的旋转角度,导致区分某些类簇的难度增大,故DDC 算法在COIL-100上表现略差。 Fig.11 Distribution of two-dimensional feature extracted from MNIST dataset图11 MNIST数据集的二维特征的分布 Table 3 Comparison of clustering performances of 4 clustering algorithms on 4 image datasets表3 在4个图像数据集上对比4个聚类算法的聚类性能 最后一组实验检测样本个数对DDC聚类精度的影响,结果列于表4。可以观察到随着样本个数的增多,CDAE-Kmeans 的聚类性能缓慢提升;而DDC 算法在30 000 个样本时有0.892 的聚类精度,随后不再增长,说明在较简单的MNIST 数据集上深度聚类模型DDC达到饱和。 Table 4 Influence of different number of data on clustering performances on MNIST表4 在MNIST上样本个数对聚类性能的影响 本文提出了一种基于深度卷积降噪编码器结合注意力的DDC 聚类模型,其中深度卷积自编码器比堆叠自编码器有更强的特征学习能力;注意力引导聚类模型获取局部特征;联合训练使特征学习和聚类指派交叠完成。这些策略提升了DDC算法的聚类能力,很好地完成了对复杂图像的聚类划分。实验结果也验证了本文的DDC具有更好的聚类划分能力。 自注意力算子提高了卷积特征的辨识能力,而DDC算法求解的核心思想是利用当前的聚类结果对卷积自编码器进行“监督”式微调,并更新聚类划分。 DDC 算法显著提升了聚类性能,但其性能受模型参数的影响较大。网络参数的初始化、优化方法、学习率的大小等对实验结果都有影响。实验中发现要根据数据和具体任务设计不同的网络结构,缺乏普遍适用性,这将是未来的研究工作之一。另外,当某一类的图像具有不确定性,即某些个体和类簇内的主体差别较大时,如何完成对它们正确归类也是将要研究的问题。
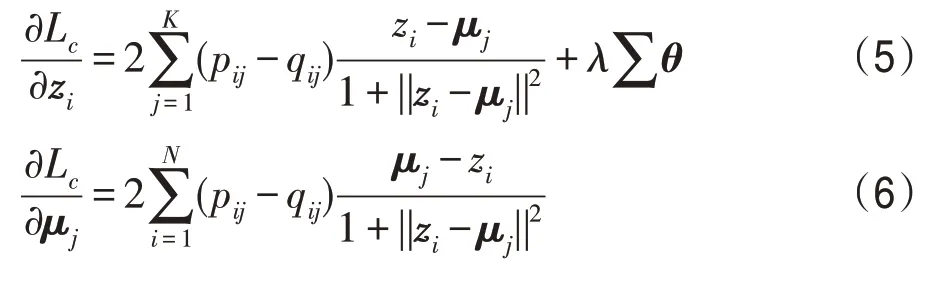
3 实验与分析
3.1 数据集

3.2 聚类评价指标

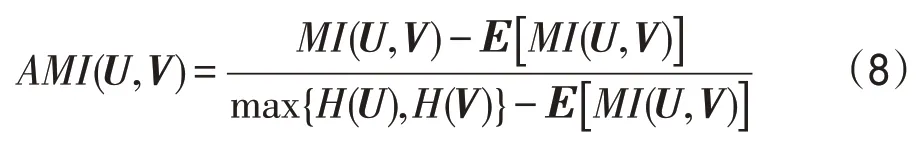
3.3 网络结构的设置

3.4 算法对噪声的有效性

3.5 DDC算法对注意力机制的有效性





3.6 与其他聚类算法的对比实验

4 结束语

