基于单种群蛙跳优化CNN的眼底图像多病变检测

任龙杰，孙 颖，丁卫平，鞠恒荣，曹金鑫

南通大学 信息科学技术学院，江苏 南通226019

彩色眼底图像是诊断眼科疾病最基本的检查方式[1]。同时，眼底图像能使人们尽早地发现各种眼部病变，如青光眼、视神经炎、黄斑病变等，方便及时、有效的治疗[2]。早期诊断与及时治疗可以有效地减少患病率。但由于中国人口数目庞大，眼科医生数量相对有限，单纯依靠医生诊断眼科疾病，需要消耗大量的时间，亟需其他方法进行大规模筛查。医学图像分析技术不仅可以大大减少医生的工作量，而且具有客观、快速、准确的优点[3]。

国内外许多学者从事视网膜病变的研究。在眼底图像病变检测方面[4]，Ganguly等人[5]针对糖尿病视网膜病变红色病变这种广泛的眼球病，提出了一种基于自适应阈值的检测方法。该方法能够对每个眼底图像使用不同强度的阈值进行处理，使其能够应用于不同摄像机获取的质量和分辨率不同的眼底图像上；Balasubramanian 等人[6]利用方向梯度直方图（HOG）特征提取和基于Gabor滤波器血管提取的视网膜眼底图像支持向量机分类方法对青光眼检测进行评估；Liu 等人[7]提出了一种基于眼底图像的杯盘比自动测量系统，可以对青光眼进行自动诊断。眼底图像分割方面[8-9]：Hossain等人[10]采用基于MRF 模型的血管分割方法，该方法相对于高度复杂的图像分割方法更有效；Samad等人[11]利用模糊C-均值对眼底图像中糖尿病视网膜病变对象的边界进行聚类和检测，可以高效、快速地分割糖尿病视网膜病变。深度学习方法在眼底图像识别中的应用也十分广泛[12-14]，Xu 等人[15]利用深度卷积神经网络方法，对彩色眼底图像针对糖尿病视网膜病变进行自动分类；Prentašić等人[16]使用卷积神经网络检测彩色眼底图像中的渗出物，实验证明CNN能有效地检测眼底图像中的渗出物。

上述研究均是对某一病种的分类，例如糖尿病引发的眼体病变判断分类，或者是对眼底图像病变、血管进行图像分割，但眼底图像中多种病变可能同时交织存在，如图1 所示，上述研究未能实现对出现于视网膜的多种病变（如硬渗出物、出血等）同时检测。本研究提出一种改进的卷积神经网络，能对同时存在于眼球的多种病变进行识别判断，例如硬渗出物、软渗出物等病变进行检测。眼底图像内容复杂，属于不同类别的图像可能相似度极高，对眼底图像进行检测识别时受到血管形变、图像本身的亮度、对比度及其他病变区域的影响[17]，采用传统的卷积神经网络进行分类检测需要大量的训练样本，而且容易陷入局部最优，训练效率较低。因此，本研究提出采用单种群蛙跳算法优化卷积神经网络的权值初始化与反向传播。通过高斯分布函数生成蛙群，不断更新最差蛙的位置，找出全局最优解并将其作为卷积神经网络的初始权值；然后监听每次训练的损失值，对异常梯度通过蛙跳算法进行修正；最后对网络最终权值进行进一步优化，最终得到了较高的病变识别准确率。

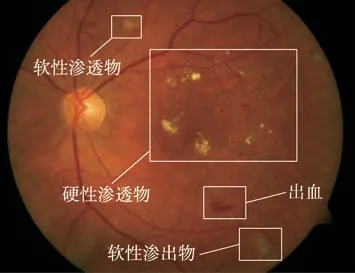
Fig.1 Fundus image with multiple lesions图1 存在多种病变的眼底图像

1 相关算法

1.1 CNN模型

卷积神经网络（convolutional neural networks，CNN）是一种多层前馈网络[18]，由LeCun等人[19]在1989年提出，作为深度学习的代表算法之一，近年来随着带注释数据量的快速增长和图形处理器单元性能的巨大提高，卷积神经网络的研究迅速兴起，并在各种任务上取得了最新的成果[20]。CNN是一种包含卷积层的深度神经网络模型，已成为当前语音分析和图像识别领域的研究热点[21]。

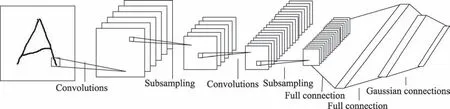
Fig.2 Classic LetNet structure图2 经典LetNet结构

时间延迟网络和LetNet-5是最早出现的网络[22]，经典的LetNet-5如图2所示。从结构上看，卷积神经网络包含输入层、隐层和输出层，其中隐层包含卷积层、池化层和全连接层。卷积层的主要功能是对图片特征进行提取，其内部包含几个卷积核，卷积核包括权重系数组成的矩阵和一个偏差值。卷积计算公式如下：

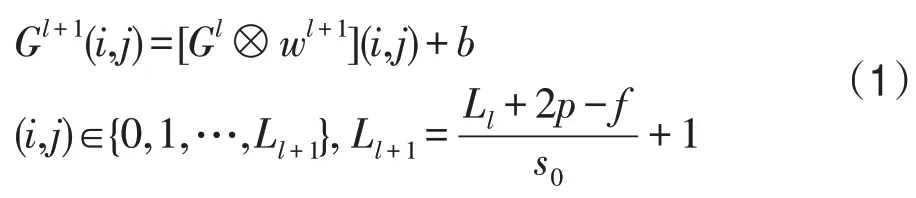
式中，b为偏差值，Gl表示第l+1层卷积的输入，Gl+1表示第l+1 层卷积的输出，Ll+1表示Gl+1的大小，wl+1表示第l+1 层的卷积核，f表示卷积层参数，s0和p分别表示Filter大小和步长。

在一次卷积计算之后，输出的特征图经过激活函数计算后会进入池化层，借助池化层来对结果进行压缩，降低数据的空间尺寸，减少网络中参数的数量，使得计算资源耗费变少，有效控制过拟合。池化也称为下采样，用S=down(C)表示。常见的池化操作主要有最大池化、平均池化等，其中应用最广泛的是最大池化[23]。最大池化如图3所示。

Fig.3 MAX pooling图3 MAX池化

经过多层卷积池化计算后，最后输出的特征图会依次按行展开，连接成向量进入全连接网络，经过多层神经网络最后得到输出。与BP 神经网络一样，卷积神经网络也是通过梯度下降来进行权值更新及反向传播。

1.2 混合蛙跳算法

混合蛙跳算法(shuffled frog leaping algorithm，SFLA)是进化计算领域中一种新兴、有效的亚启发式群体计算技术[24]，一种结合了遗传基因的模因演算算法[25]，主要包含局部搜索和全局信息交换两部分，局部搜索和全局信息交换一直持续进行到满足收敛条件[26]。SFLA 的基本工作流程：随机生成由F只青蛙组成的蛙p={f1,f2,…,fF}，则第i只青蛙表示为fi=[x1,x2,…,xs]，s表示每只青蛙的维度。生成青蛙后，将所有青蛙按适应值进行降序排序，划分成M个种群，划分规则为：

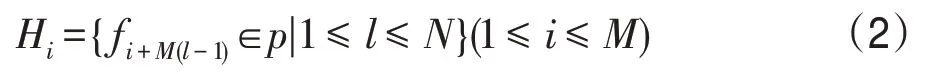
每个种群包含有N只青蛙，满足F=M×N。划分种群之后，记录全局最优蛙fg，在每个种群内部进行局部搜索，在第j次局部搜索后种群内适应值最差蛙表示为fw(j)，适应值最优蛙表示为fb(j)，对每个子种群中的最差蛙循环更新，更新公式如下：

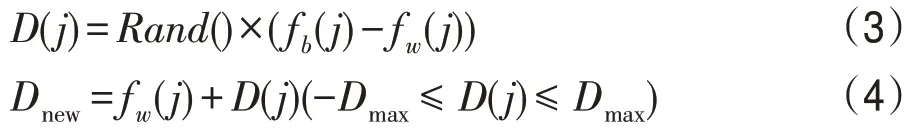
其中，Rand()表示0 到1 之间的随机数，Dmax表示最大蛙跳距离。青蛙位置更新之后，如果没有得到改进，则将fg代替fw(j)，如果仍然没有改进，则随机产生一个新的青蛙取代fw(j)。

当所有种群经过Umem次搜索时，将所有青蛙混合到一起，按适应值重新排序，重新划分子种群，使得各个种群中青蛙的模因信息能够充分传递，然后继续进行局部搜索。重复以上步骤，直至符合收敛条件，算法结束。

2 基于单种群蛙跳优化的CNN模型

针对眼底图像的复杂性，本研究将单种群蛙跳引入卷积神经网络权值初始化和权值更新中。通过不断更新最差蛙的位置，寻找出全局最优蛙作为网络的初始权值。在网络迭代过程中，监听每次计算的损失值，对产生异常损失值的网络权值通过蛙跳算法进行纠正。采用单种群蛙跳优化的卷积神经网络算法（single population frog-leaping optimization convolutional neural network algorithm，SFCNN）流程如图4所示。

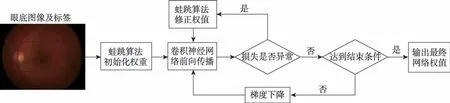
Fig.4 SFCNN algorithm图4 SFCNN算法

2.1 基于单种群蛙跳算法的权值初始化

卷积神经网络中，卷积核、全连接层权值等一般采用随机的方式生成，由于眼底图像中多种病变可能同时存在，呈现不规则分布，并且健康眼底图像与病变眼底图像区分不明显，如图5所示。当网络随机生成的权值太差时，网络就需要花费更多的时间和样本进行梯度下降运算来对权值进行修正，同时也容易使网络陷入局部最优，影响最终结果。针对这个问题，本研究提出引入单种群蛙跳算法对卷积神经网络权值初始化。

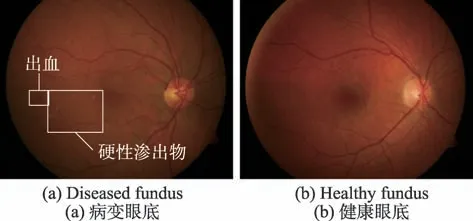
Fig.5 Similar fundus images图5 相似眼底图像

混合蛙跳算法是一种亚启发式群体进化算法，具有优良的全局搜索能力，能够有效计算出全局最优解，但是将其直接应用于本研究中的权值初始化会产生大量的计算，增加算法整体运行的时间成本，影响效率，因此本研究通过简化混合蛙跳算法，提出了单种群蛙跳算法。与混合蛙跳算法不同，本文不再对初始样本进行种群的划分，而是将所有青蛙视为一个种群，直接进行全局寻优，并且在蛙跳规则上做了一些改进。

算法具体步骤如下：

算法1权值初始化算法

步骤1参数初始化。确定青蛙数量m，根据高斯分布公式：

其中，设置μ=0，σ=1。

步骤2排序。将所有未计算损失值的青蛙带入如图2所示的CNN模型，从训练图像库中随机选取n张图像作为参照图像，进行CNN前向传播，计算每只青蛙的损失值，这里的损失值计算函数即为单蛙群算法的适应度函数，损失计算公式为：

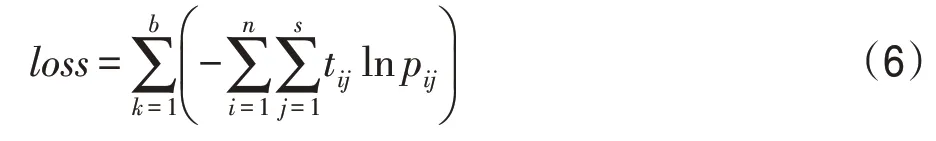
其中，p表示网络输出值；t表示真实值；s表示每组病变标签的维度；b表示需要同时检测的视网膜病变种类数。根据适应度函数对所有青蛙进行升序排序。

步骤3种群内进行搜索和位置更新。由步骤2可以得出最优蛙fb和最差蛙fw，通过位置更新函数对最差蛙的位置进行更新。针对青蛙位置更新，本研究在传统蛙跳公式中添加了一个偏移量，同时适当增大Rand()函数的随机区间，公式如下：

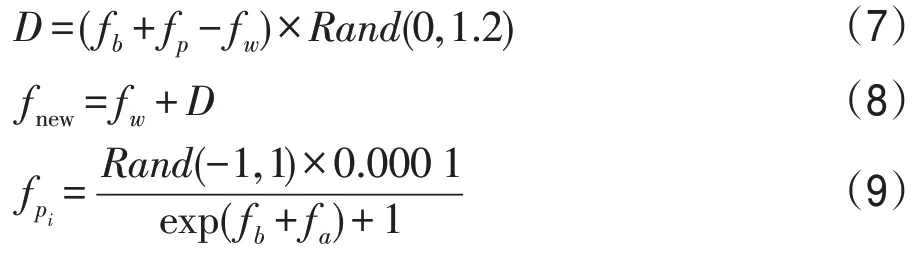
式中，fp表示偏移量，其维度与每只青蛙的维度相同；fpi表示fp中第i个维度上的值；fnew表示更新后的青蛙。通过添加偏移量的方式，能够有效提高蛙跳的性能，增大随机区间使得算法更容易寻找到最优解。将本步骤提到的跳跃方式映射到二维坐标如图6所示。

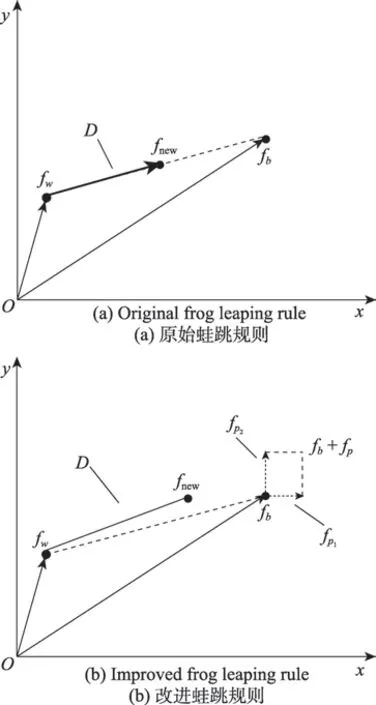
Fig.6 Improvement of frog leaping rule图6 蛙跳规则改进

步骤4检验计算停止条件。判断算法是否满足收敛条件，如果满足则停止算法，将最优蛙的值作为卷积神经网络的初始权值，否则转到步骤3。

2.2 基于单种群蛙跳算法的权值初始化

传统的CNN 反向传播本质上就是梯度下降法，通过前向传播计算得到的损失值更新网络参数，从而找到最优解。而眼底图像存在血管密布、病变处交织重叠、某些病变处十分微小等问题，并且受拍摄时光照影响严重，因此对眼底图像进行多种病变识别难度较大，采用梯度下降算法容易出现损失值变化幅度较大的异常情况，影响算法的执行效率，甚至会引起算法收敛到局部最优等问题。针对上述问题，本研究采用单种群蛙跳算法对卷积神经网络反向传播的较差梯度进行修正。

在网络迭代过程中，监听每次前向传播计算得到的损失值，如果第i次计算的损失值与i-1 次的损失值差值的绝对值大于阈值o，即|li-li-1|>o，则认为第i次前向传播中的权值为无效权值，采用单种群蛙跳算法重新寻找最优权值；在卷积神经网络符合结束条件后，得到训练完成的权值fqb，最终算法再执行一次单种群蛙跳计算，通过最后一次的单种群蛙跳寻优可以直接有效避免局部最优。

算法2权值更新算法

步骤1输入样本。输入眼底图像和对应的标签，对标签进行one-hot编码。

步骤2卷积，池化。对输入的眼底图像进行多层的卷积与池化操作，每次池化计算结束对输出结果采用ReLU函数进行激活。

步骤3全连接计算。经过多层全连接计算得到预测值，将预测值带入softmax()函数计算得出结果后，通过式（6）计算损失值。

步骤4误差值比对。判断本次迭代的损失值与前一次损失值差的绝对值是否大于阈值o，如果不大于阈值，跳转步骤10，否则执行步骤5。

步骤5初始化参数。记录第i-1 次前向传播的权值wb，设置青蛙数c。

步骤6生成青蛙。与上文提到的采用高斯分布生成青蛙的方式不同，这里的青蛙主要围绕wb生成，生成公式如下：

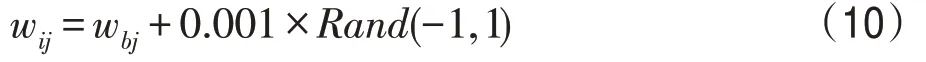
其中，1 ≤i≤c-1，wij表示生成的第i只青蛙的第j个维度上的值，n表示青蛙总数。此时蛙群中，必然存在青蛙wg满足条件lg≤lb，lg和lb分别为wg和wb的损失值。

步骤7排序。随机抽取少量训练图片作为输入值，将c中所有青蛙带入图2所示的CNN模型中，根据式（6）计算损失值，并将所有青蛙按损失值降序排序。

步骤8种群内进行搜索和位置更新。此步骤与2.1节中步骤3相同。

步骤9检验蛙跳停止条件。判断算法是否满足收敛条件，如果满足则停止算法，将最优蛙的值更新网络权值，否则转到步骤8。

步骤10检验网络停止条件。判断网络是否符合收敛条件，如果满足则停止迭代，否则跳转到步骤1。

步骤11优化最终权值。算法训练结束后，网络中的权值即为最终权值，将最终权值作为初始蛙wb，通过式（10）生成蛙群，然后依次执行步骤7～9，最终得到全局最优蛙wqb即为算法最终训练完成的权值。

算法流程图如图7所示。

3 SFCNN眼底图形多病变检测实验

为验证本研究中算法的有效性，实验算法采用Python3.5 编程实现，实验环境为Windows10/2.6 GHz/8 GB PC，实验中所有彩色视网膜眼底图像均来自公共数据库DRIVE（digital retinal images for vessel extraction）数据库[27]和糖尿病性视网膜病变图像数据库DIAREDB1。

针对眼底图像的复杂性，如受光照影响、病变处交织重叠等，实验中首先采用单种群蛙跳算法寻找最优初始权值，然后监听卷积神经网络每次前向传播计算的损失值，发现异常损失值时，采用单种群蛙跳算法对产生异常损失值的权值进行修正，从而提高网络执行效率，避免网络陷入局部最优。实验流程如图8所示。

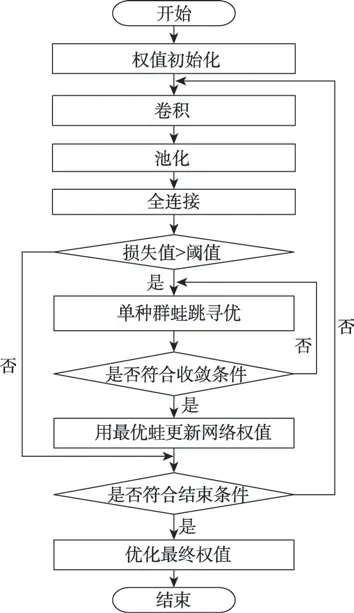
Fig.7 Weight optimization flow chart图7 权值优化流程图

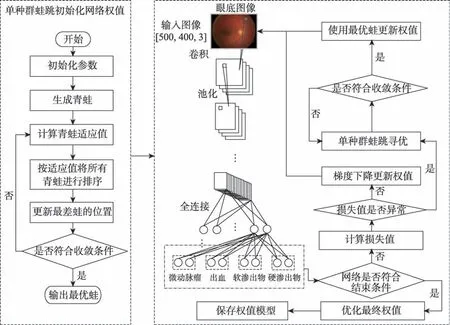
Fig.8 SFCNN algorithm experiment图8 SFCNN算法实验

3.1 交叉熵损失计算方法

实验同时对硬渗出物、出血、微动脉瘤和四种视网膜病变进行检测，首先对每张眼底图像进行标签标注，并进行one-hot编码，组成包含8个元素的二维数组，如y_true=[[1,0],[0,1],[1,0],[1,0]]，8 个元素被分成4 组，每组元素第一位值为1 代表没有病变，第二位值为1 代表发生病变。经过卷积神经网络前向传播计算后的预测值y_predict也是一个包含8 个元素的二维数组，将预测值中的每组分别进行softmax()计算，然后通过式（6）计算得到损失值。

3.2 实验结果分析

单种群蛙跳算法通过全局寻优，找到最优的初始权值，能够有效降低网络初始损失值，提高网络计算效率，甚至能够对最后的分类结果产生较大的影响。如表1 所示，可以看出，通过蛙跳算法寻优后的初始值第一次损失值计算相比较于传统高斯分布随机产生的初始损失值降低了很多，由于眼底图像有一定的复杂性，不同病变的图像可能存在一定的相似性，这使得传统方法生成的初始网络权值稳定性较差，计算的损失值优劣差距较大，较差的初始参数就需要更多步梯度下降计算来优化，并且还可能导致算法陷入局部最优。因此通过单种群蛙跳算法优化初始值，能有效保证卷积神经网络在眼底图像多标签分类中初始值生成的稳定性，并且优质的网络初始权值，可以有效减少网络迭代次数，提高网络执行效率，在一定程度上避免网络陷入局部最优。

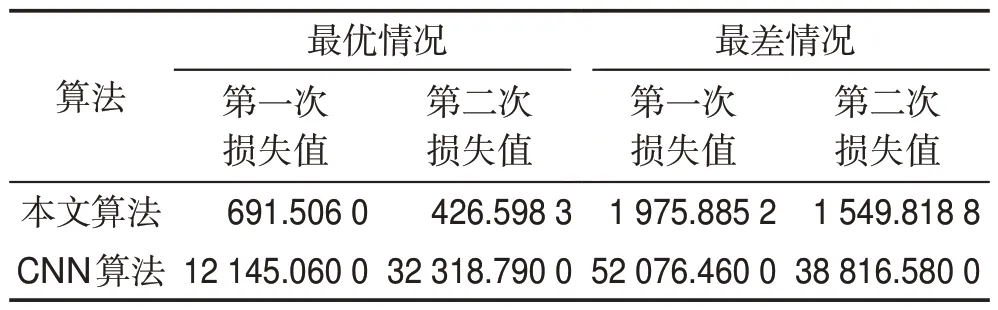
Table 1 Comparison table of initial loss表1 初始损失值对比表

随着迭代次数的增加，网络的损失值呈曲折下降趋势，但是由于眼底图像图片相似性高，受光照、微小病变点影响严重，传统的卷积神经网络误差会出现波动值较大的情况，这就会影响算法的执行效率，甚至会导致陷入局部最优，如图9所示。

本研究通过监听误差值与阈值进行比较，针对造成异常损失值的权值，通过单种群蛙跳算法进行纠正。权值比较方法如下：

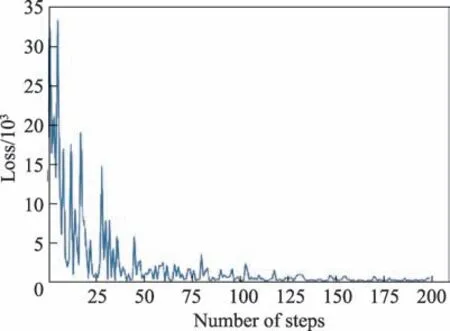
Fig.9 Loss reduction chart of CNN图9 CNN损失下降折线图

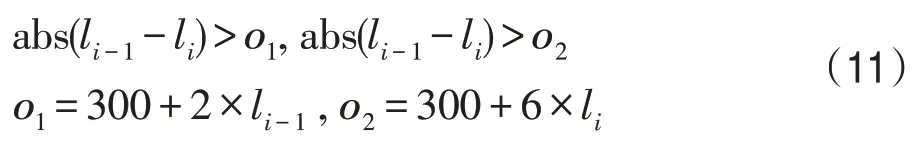
其中，o1和o2是定义的两个阈值，li为第i次迭代的损失值，abs()为取绝对值函数。通过单种群蛙跳算法优化之后的损失值折线图如图10 所示，可以看出相对于优化之前，优化之后的波动更小，过大波动较少，从而有效减少陷入局部最优的可能性。

Fig.10 Loss reduction chart of improved algorithm图10 改进算法损失下降折线图

在卷积神经网络执行结束后，再对网络最终权值进行一次单种群蛙跳寻优，可以直接有效避免陷入局部最优，同时也是对网络权值的进一步优化，使其对于光照过亮、光照过暗、病变交织重叠等复杂眼底图像的病变检测更为准确。图11 展示了CNN 和本文算法对三种受不同因素影响的复杂眼底图像的多病变检测效果，图中HE（hard exudates）表示硬渗出物，SE（soft exudates）表示软渗出物，M（microaneurysms）表示微动脉瘤，H（hemorrhages）表示出血，Loss 表示网络对四种病变检测的总损失值（精确到小数点后两位）。图12 显示了两种方法对相似眼底图像进行多病变识别的准确度和损失之和，从图中可以看出，SFCNN 算法对此类眼底图像的准确率更高，损失值更低。从图中可以看出，传统CNN算法在部分眼底图像上个别病变检测不准确，而SFCNN 在这类眼底图像上准确率较高，并且损失值更小。

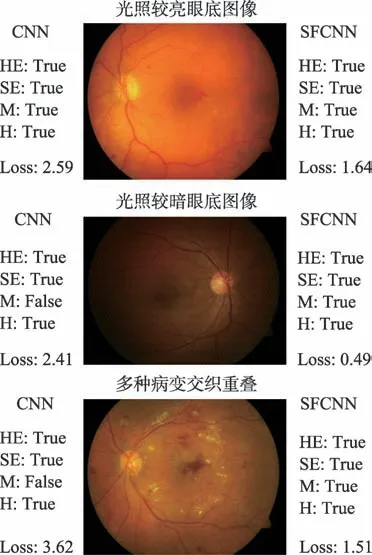
Fig.11 Complex fundus image detection图11 复杂眼底图像检测

实验中卷积神经网络部分主要通过两层卷积、两层池化层和一层全连接层对眼底图像进行多病变分类检测。主要从准确率（accuracy）和灵敏度（sensitivity）两方面对算法进行评价，公式分别如下：

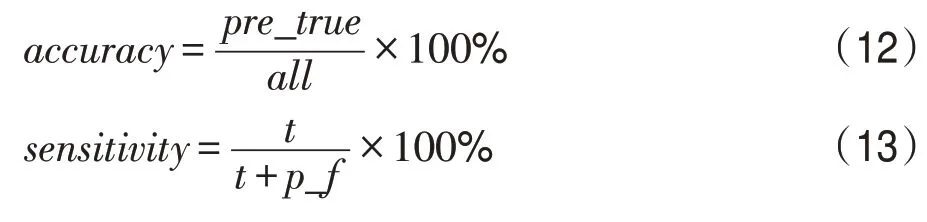
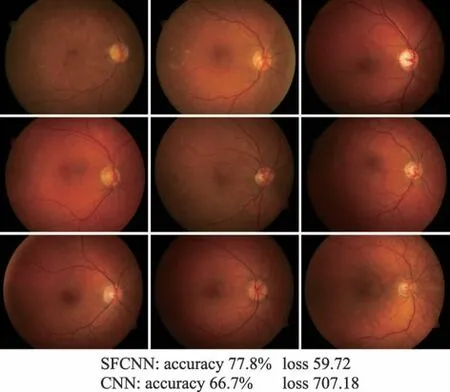
Fig.12 Similar fundus images图12 相似眼底图像

其中，pre_true表示识别正确的眼底图像数量，t表示真存在病变的数量，p_f表示假存在病变的数量，并且加入综合识别率和整体识别率作为参考，其中综合识别率为p=(c1+c2+c3+c4)/n，这里c1、c2、c3、c4分别代表四种病变识别正确的数量，n代表测试集样本总数；整体识别率为每个样本同时对四种病变检测正确的百分比。从表2 和图13 中可以看出，相对于SFLA-CNN、AlexNet 神经网络、LetNet-5 神经网络，SFCNN 都有不同程度的提高。图14 展示了SFCNN 和SFLA-CNN 算法的运行时间对比，分别取运行150步、300步、500步、1 000步、1 500步和2 000步的3次运算时间平均值。从图中可以看出，运行时间随步数增加而增长，具有一定的随机性，但相同运行次数的SFLA-CNN 的运行时间普遍要比SFCNN的运行时间长，因此通过对混合蛙跳算法进行改进后，更适合用于本文的改进方式中。

实验还将本文提出的SFCNN算法与传统的CNN算法、SVM[28]算法和KPCA+SVM 融合算法[29]单独对眼底图像硬渗出物分类检测准确率进行比较，检测准确率用柱状图表示为如图15所示。从分类效果柱状图可以看出，SFCNN 算法在多病变检测和单一病变检测方面，相对于已有算法，准确率均有所提高，证明了单种群蛙跳优化的卷积神经网络具有一定的优越性及有效性。

Table 2 Comparison of experimental accuracy表2 实验准确率对比 %

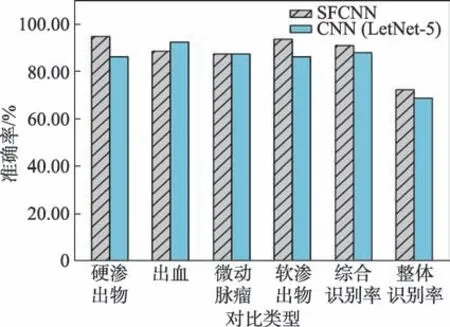
Fig.13 Accuracy contrast of multiple lesions图13 多病变准确率对比

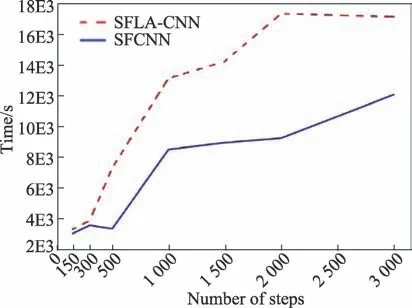
Fig.14 Comparison of time图14 时间对比

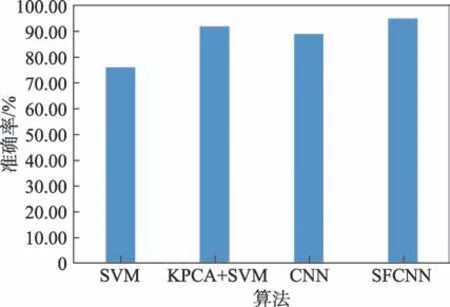
Fig.15 Hard exudation detection accuracy图15 硬渗出检测准确率

4 结束语

本文提出利用简化的SFLA算法，将全局视为一个种群进行蛙跳计算，提出单种群蛙跳算法优化CNN 应用于眼底图像多种病变的识别。由于CNN的初始权值选择存在不确定性，容易影响网络执行效率，CNN自身的反向传播计算容易陷入局部最优，本文提出采用单种群蛙跳算法来对损失值异常的权值进行优化，修正参数值，避免算法陷入局部最优，提高病变的识别率，降低训练成本。

对于多分类的准确率进一步提升，今后需要继续对训练样本库进行扩充，提高样本和标签质量；同时对于执行时间方面，结合最新蛙跳算法研究成果，寻找效率更高的改进方法提高算法训练时效。在后续研究中，可以探索卷积神经网络在眼底图像中的分割、病变定位等应用，以解决传统方法难以解决的综合问题。