蜗杆砂轮磨齿加工参数优化

王利亭 赵秀栩 李 娇

1.武汉理工大学机电工程学院，武汉，430070 2.韶能集团韶关宏大齿轮有限公司，韶关，512000

0 引言

在齿轮实际服役过程中，齿面粗糙度对齿轮的耐疲劳性、耐磨性、耐腐蚀性和传动质量都有显著影响[1-2]。日本机械学会对齿轮传动失效实例的调查结果显示，约74%的齿轮传动接触疲劳失效与齿轮啮合时的齿面粗糙度的大小有直接关系[3-4]，因此，在齿轮制造过程中必须严格保证齿轮最终表面的粗糙度。

蜗杆砂轮磨齿加工是展成法加工渐开线齿轮轮廓的方法之一，通过蜗杆砂轮与待加工齿轮的啮合传动来磨削齿轮齿面待加工余量，具有加工效率高、加工性能稳定、产品质量高等优点，被广泛用于中小模数齿轮的精加工。目前，针对蜗杆砂轮磨齿加工的研究主要有三个方面：①基于蜗杆砂轮磨齿机各轴的运动特点，从数控系统出发对蜗杆砂轮磨齿机各运动轴的误差进行补偿，从而提高齿向、齿距和齿形等齿轮几何精度[5-8]；②运用某种径向热误差补偿方法[9-10]减小机床热误差对齿轮M值(即跨棒距，反映齿轮分度圆齿厚的一项测量指标)的影响，提高齿轮的齿厚精度和运动精度；③采用改变蜗杆砂轮冲程速度的加工方法形成不规则的齿面纹理，进而减小齿轮的啮合噪声[11-12]。现有的研究很少从磨削参数的角度对齿面质量进行改进，本文首先以蜗杆砂轮磨削20CrMnTi齿轮试验为基础，采用均匀设计磨削试验，利用德国马尔Xcr20粗糙度仪测量零件齿面粗糙度，研究磨削参数(砂轮线速度vs、砂轮沿齿轮轴向进给速度vw、磨削厚度ap)对蜗杆砂轮磨削加工20CrMnTi齿轮齿面粗糙度的影响。然后基于均匀设计试验，对试验数据采用二级逐步回归分析方法，建立磨削参数与齿面粗糙度的多元回归预测模型。最后构建以加工效率、齿面粗糙度为目标的多目标优化模型，采用粒子群优化算法对加工参数进行优化，寻求加工效率高、齿面粗糙度小的磨削参数。

1 磨削试验

1.1 试验条件

试验设备为德国KAPP NILES公司生产的KX500 FLEX数控磨齿机，磨削砂轮为德国BIKE公司生产的立方氮化硼(CBN)砂轮，砂轮的基本参数如表1所示。试验所用齿轮零件为某变速箱高速行星轮，材料为20CrMnTi，齿轮零件基本参数见表2，材料力学性能见表3。

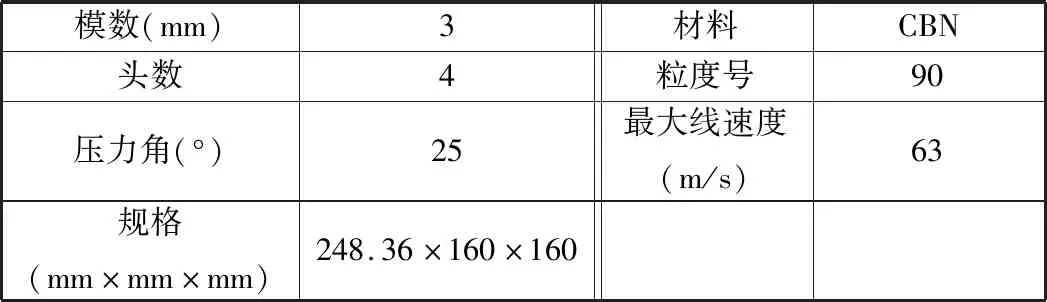
表1 砂轮基本参数表Tab.1 Basic parameters of grinding wheel

表2 试验零件基本参数Tab.2 Basic parameters of test parts

表3 20CrMnTi力学性能Tab.3 Mechanical properties of 20CrMnTi

1.2 试验方法

蜗杆砂轮磨削是一个动态和高度非线性的复杂过程，影响磨削表面粗糙度的因素有磨削加工运动轨迹、磨削参数(砂轮线速度vs、砂轮沿齿轮轴向进给速度vw、磨削厚度ap)、砂轮特性与形貌、砂轮是否磨损与修整、磨削液、工件材料、工艺系统的刚度及其动态特性等[13]。

试验的思路是：实际加工生产中，机床、砂轮、冷却润滑液、工件材料等相对固定，根据具体的加工对象，变更可控制的磨削参数，采用均匀设计试验方法，探究磨削参数对20CrMnTi齿轮齿面粗糙度的影响。以磨削参数为影响因素，齿面粗糙度为试验指标，根据车间操作者的磨削经验以及砂轮制造商所提供的磨削参数范围，利用数据处理系统获得的均匀设计试验组如表4所示。

表4 均匀设计试验表Tab.4 Uniform design test table

在KX500 FLEX数控磨齿机上依据均匀设计试验的试验参数进行齿轮工件磨削加工，将加工好的工件清洗干燥后，采用德国马尔Xcr20粗糙度仪测量零件齿面粗糙度。

2 试验结果与齿面粗糙度模型的建立

2.1 试验结果与分析

按照表4中的均匀设计方案完成9组试验，从每组试验中选取1个样品进行齿面粗糙度检测。其中每个齿面测量2个粗糙度数值，取其平均值作为该齿面粗糙度值，详细数据如表5所示。

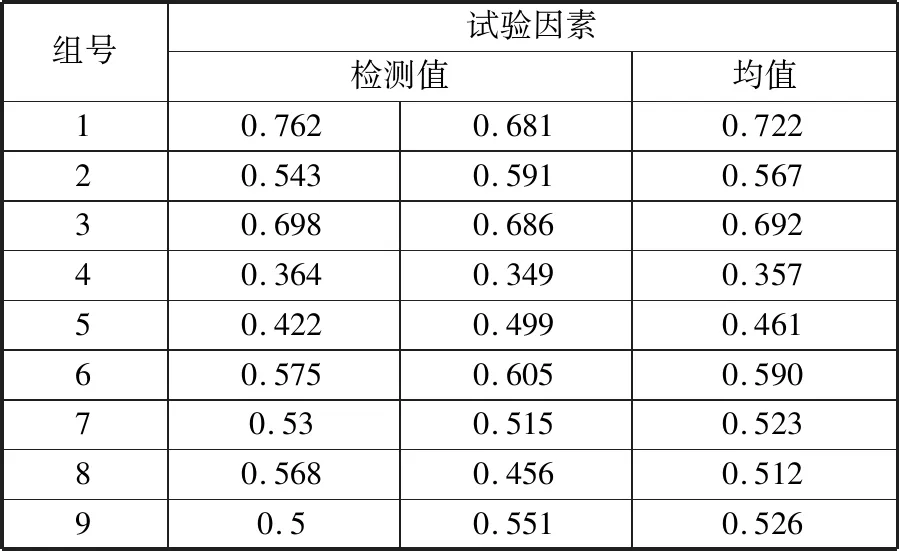
表5 齿面粗糙度检测结果Tab.5 Test results of tooth surface roughness

试验自变量水平的设置是否能够显著地影响因变量，对试验结果的分析非常重要。本节采用单因素方差分析法和多因素方差分析法验证因变量水平设置的有效性。方差分析又称“F检验”，用于两个或两个以上样本均值差异的显著性检验。该检验方法的计算公式为

(1)

式中，SA、SE分别为组间平方和与组内平方和；m为因素的水平等级；n为样本个数。

将齿面粗糙度检测值进行单因素方差分析，其中砂轮线速度与齿面粗糙度单因素方差分析结果如表6所示。

由表6可以看出，R2=0.926 95，P值接近于0，表示各组间数据显著性不同，表明在砂轮线速度水平设置上具有一定的显著性，试验因素水平设置合理；对砂轮沿齿轮轴向进给速度、磨削厚度进行相应的分析，结果也同样表明试验因素水平设置合理。对齿面粗糙度数据进行多因素方差分析，结果如表7所示。

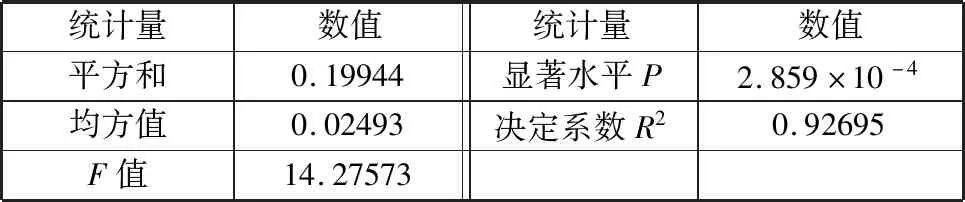
表6 砂轮线速度与齿面粗糙度单因素方差分析结果Tab.6 Results of single-factor analysis of variance between grinding wheel linear velocity and tooth surface roughness

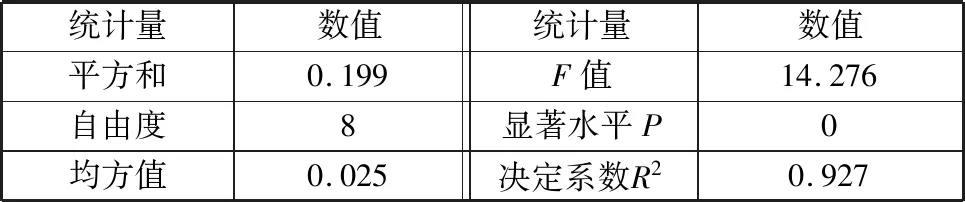
表7 齿面粗糙度多因素方差分析结果Tab.7 Results of multi-factor analysis of variance for tooth surface roughness

由齿面粗糙度的多因素分析结果可知，R2=0.927，P值为0，表示多因素水平设置所得结果显著不同，试验因素水平综合设置具有一定的有效性。

2.2 齿面粗糙度模型的建立

将齿面粗糙度数据导入数据处理系统，选择二次多项式逐步回归得到二次回归方程如下：

0.1421x2x3

(2)

式中，y1为齿面粗糙度；x1、x2、x3分别为砂轮线速度、砂轮沿齿轮轴向进给速度和磨削厚度。

将模型计算所得粗糙度值与实测粗糙度值进行比较，结果如图1所示，模型计算值与实测值比较接近。

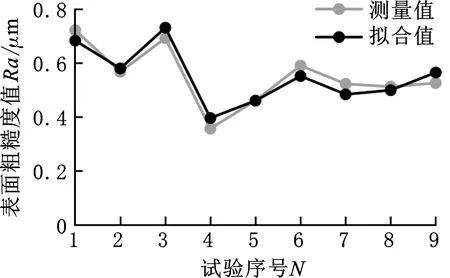
图1 齿面粗糙度测试数据和拟合数据对比图Fig.1 Comparison of tooth surface roughness test data and fitting data

表8所示为回归模型显著性检验结果。F=23.2078>F0.05(6，2)=3.374，表明回归效果显著，决定系数R2=0.9059，表明因变量与自变量高度相关。从拟合图和回归分析结果可以看出拟合情况非常理想。

表8 齿面粗糙度回归模型显著性检验Tab.8 Significance test of tooth surface roughness regression model

表9所示为回归模型中各项显著性检验结果，可以看出齿面粗糙度模型中各项与齿面粗糙度y值之间的偏相关性，即该项值发生变化时对y值的影响趋势。偏相关值范围是-1～1，“-1”表示完全负相关，而“1”表示完全正相关，中间值“0”则表示不相关。可以看出：①砂轮线速度x1与齿面粗糙度y之间的关系为高度负相关，即当砂轮线速度增大时，齿面粗糙度值会明显减小。这是因为提高砂轮速度后，每颗磨粒切下的磨屑变薄，磨粒在工件表面上产生的理论残留面积高度变小；另外，砂轮速度的提高有利于磨屑的形成，磨削表面因塑性侧向隆起的高度也会变小[14]。因此，砂轮速度增大后，既可提高磨削效率，又可减小齿面粗糙度值。②砂轮沿齿轮轴向进给速度x2的平方与齿面粗糙度值y的偏相关值为0.8777，表示它们之间的正相关性较高，即齿面粗糙度值随砂轮沿齿轮轴向进给速度的增大而增大。其原因是随着轴向进给速度的增大，在单位时间内磨削齿面的磨粒切刃数减少，使得单位面积齿面上形成的磨削残留高度增大；此外，磨床的颤振增强也会对齿面粗糙度产生一定的影响，使粗糙度数值有增大的趋势[15]。③磨削厚度x3的平方与齿面粗糙度值y的偏相关值为0.8505，表示它们之间的正相关性较高，即齿面粗糙度值随磨削厚度的增大而增大。这是由于磨削厚度的增大，使得单颗磨粒的最大切削厚度增大，划痕数减少，从而增大齿轮磨削材料的塑形变形，使得磨粒切削刃通过磨削工作区时在齿轮表面留下的切痕深度增大，从而使齿轮表面变得更加粗糙[13]。同时，各因素之间还存在交互影响，并且偏相关性绝对值都接近于1，表明加工参数之间的交互作用也会显著影响齿面粗糙度值。

表9 齿面粗糙度模型各项显著性检验Tab.9 Significance test of tooth surface roughness model

3 多目标优化模型的建立与求解

3.1 多目标优化模型

优化蜗杆砂轮磨削加工20CrMnTi齿轮参数时，在保证加工质量的情况下应提高加工效率。磨齿加工时间体现加工效率，根据加工运动过程，加工时间计算公式如下：

(3)

式中，y2为加工时间，min；L为齿轮齿面宽，mm。

根据多目标加工工艺参数优化的特点，采用线性加权法将多目标问题变为单目标问题求解，即为求解f(x)的最小值：

minf(x)=W1y1+W2y2

(4)

其中，W1、W2为各目标的权重，W1、W2∈(0，1)，W1+W1=1。为将各目标的量纲进行统一，对各目标进行归一化处理，本文选用最小值-最大值归一化方法，其表达式为

x′=(x-xmin)/(xmax-xmin)

(5)

即该目标函数化解为

(6)

约束条件如下。

(1)砂轮线速度约束。为保证砂轮的使用性能，加工过程中一般不允许砂轮线速度超过砂轮厂家规定的上限值，但是过低的砂轮线速度又会影响加工效率，设置31 m/s≤vs≤63 m/s。

(2)砂轮轴向进给速度约束。砂轮轴向进给速度直接决定着加工时间，进给速度过大，机床刚度不足容易产生齿面振纹，影响齿轮质量，而过小则会使得加工时间过长而影响生产效率，设置80 mm/min≤vw≤176 mm/min。

(3)磨削厚度约束。磨削厚度过大会影响齿面粗糙度值并造成齿轮烧伤，过小则会增加加工次数从而增加加工时间，设置0.015 mm≤ap≤0.79 mm。

(4)表面烧伤约束。齿面烧伤会影响齿面性能，因此必须保证加工过程中齿轮不被烧伤。根据小野浩二公式[16]，需要满足：

(7)

式中，da0为砂轮直径，mm；Cb为材料烧伤临界值，m·mm/min，不同的加工环境取不同的值。

在企业实际加工过程中发现，当Cb值为7226 m·mm/min时发生轻微烧伤(砂轮线速度为63 m/s，磨削厚度为0.015 mm)，因此将此值作为临界值，即

(8)

联合上述目标等式和约束条件，完整的优化模型为

(9)

式中，T为加工时间；Tmax、Tmin分别为最大加工时间和最小加工时间。

3.2 优化算法

粒子群优化(particle swarm optimization，PSO)[17]是一种通过评价函数来衡量个体的优劣程度，同时根据评价函数得到的适应度值在种群进行随机搜索的方法[18]。PSO算法通过个体的随机速度来改变个体，没有如交叉、变异等遗传操作，其计算过程容易；另一方面，PSO算法只有当前全局最优解将信息单向传递给另一粒子，这使得粒子的搜索更新伴随着当前全局最优解，在搜索性能上略优于遗传算法。

PSO算法首先初始化一群随机粒子，然后通过迭代逐渐逼近最优解。设在n维空间里有m个微粒，每个粒子的坐标定义为xi=(xi1，xi2，…，xin)，目标函数作为适应度值f，在每一次迭代中，计算各个粒子的目标函数值，并将两个“极值”进行比较，将较优的解保存为当前极值。每个粒子的当前速度表示为Vi=(Vi1，Vi2，…，Vin)；每个粒子所经过的最好位置表示为Pi=(Pi1，Pi2，…，Pin)。粒子通过下式更新自己的速度与位置[14]：

Vi(t+1)=ωVi(t)+c1r1(Pi-xi(t))+

c2r2(Pb-xi(t))

(10)

xi(t+1)=xi(t)+Vi(t+1)

(11)

式中，Vi(t)为粒子i在第t代的速度；ω为粒子的惯性权重；c1、c2为学习因子；r1、r2为两个介于0～1之间的相互独立的随机数；Pb为所有粒子所经过的最好位置(全局历史最优位置)。

粒子群优化算法流程如图2所示。

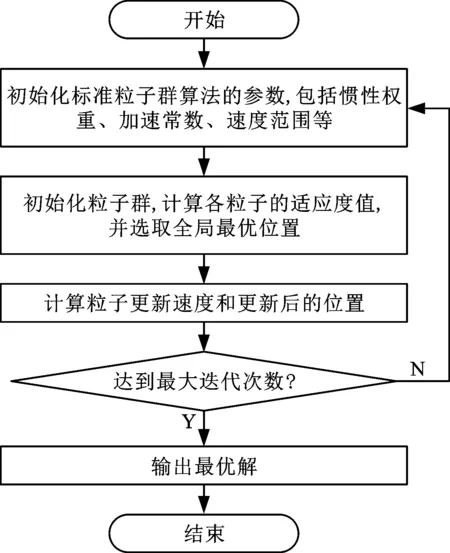
图2 粒子群优化算法流程Fig.2 Flow chart of PSO

3.3 优化结果

在MATLAB中编写粒子群优化算法，群体大小设为50，最大迭代次数设为1000，学习因子c1=c2=2，惯性权重ω=1，r1=r2=0.95；考虑加工效率与表面质量，选用权重系数W1=0.4、W2=0.6进行优化求解，车间现有实际加工、优化计算结果和采用优化参数的实际加工结果对比如表10所示。

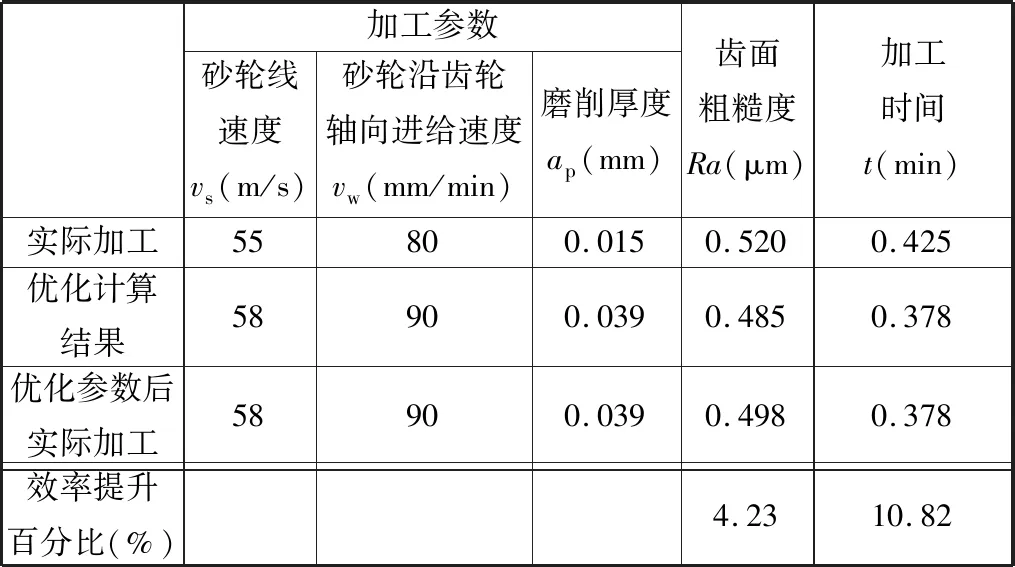
表10 优化结果对比Tab.10 Comparison of optimization results

由表10可知，与实际加工参数对比，采用优化求解参数进行实际加工获得的齿面粗糙度值比实际加工值减小0.022 μm；加工时间缩短0.046 min，生产效率提高10.82%。综上，优化结果能显著提高加工效率和减小齿面粗糙度。

4 结论

(1)本文以蜗杆砂轮磨削加工20CrMnTi齿轮为研究对象，选择均匀设计试验，根据试验数据建立了齿面粗糙度预测模型，通过回归模型统计量、模型拟合数据与试验所测数据对比可知，建立的齿面粗糙度预测模型可靠，能够对蜗杆砂轮磨削加工20CrMnTi齿轮时合理选择切削参数提供指导。

(2)由预测模型可知，齿面粗糙度随砂轮线速度增大而减小，随砂轮沿齿轮轴向进给速度和磨削厚度的增大而增大。

(3)与车间现有实际加工相比，采用优化后的磨削参数进行加工，生产效率可提高10.82%，齿面粗糙度可减小0.022 μm。