连接区域灌封的复合材料蜂窝夹芯结构承载能力研究
王 汝
(浙江机电职业技术学院智能制造学院,浙江 杭州 310053)
蜂窝夹芯结构是由上、下面板及蜂窝芯通过胶黏剂胶接构成,此类结构因其具有力学性能优、减重效果好被各行各业广泛采用[1]。蜂窝夹芯结构多通过连接件与其他构件装配在一起,主要受拉、拔载荷的作用,连接件通常为其主要承力部件。结构的失效区域多分布于连接件的周围。蜂窝夹芯结构的失效形式复杂多样,主要有蜂窝面板的破坏、连接件的失效、蜂窝芯的变形失效等等[2]。
在蜂窝夹芯结构的设计以及优化过程中,更多学者倾向于采用实验结合数值分析的方法进行研究。Bai等[3]采用非接触数字测量并结合实验及数值仿真的方法,研究了蜂窝夹芯结构的承载能力及失效机理;Demelio等[4]结合实验与数值仿真研究了蜂窝夹芯结构在不同载荷下的承载能力及失效机理。由于复合材料蜂窝夹芯结构复杂多变,在对其进行计算时多采用等效板理论进行简化计算,目前较常用的是等效三明治理论。
本文首先对连接区域灌封后的复合材料蜂窝夹芯板进行拉拔实验研究,得到结构的极限承载能力以及破坏模式,然后在有限元分析软件ANASYS中建立蜂窝夹芯结构的计算模型,并对其进行数值模拟计算,比对实验结果和计算结果,验证计算结果的有效性。
1 实验
1.1 实验件及设备
本文采用的蜂窝夹芯结构实验件如图1所示,两块边长为170.0 mm、厚度为23.9 mm的方形蜂窝夹芯板通过螺栓连接件错开90°装配连接,对蜂窝夹芯结构中间的四边形(边长为60 mm)区域的蜂窝进行灌封胶填充,蜂窝夹芯板边缘的孔为实验载荷加载孔,为了避免在结构失效前出现加载区域的失效,在实验件的加载孔周围也填充了灌封胶,以提高加载区域的承载能力。依据实验测试标准(NASM 1312-8)设计的卡具如图2所示,实验卡具分上、下两套,均由底座和台阶销组成,根据静力分析结果,底座和台阶销选用45钢。
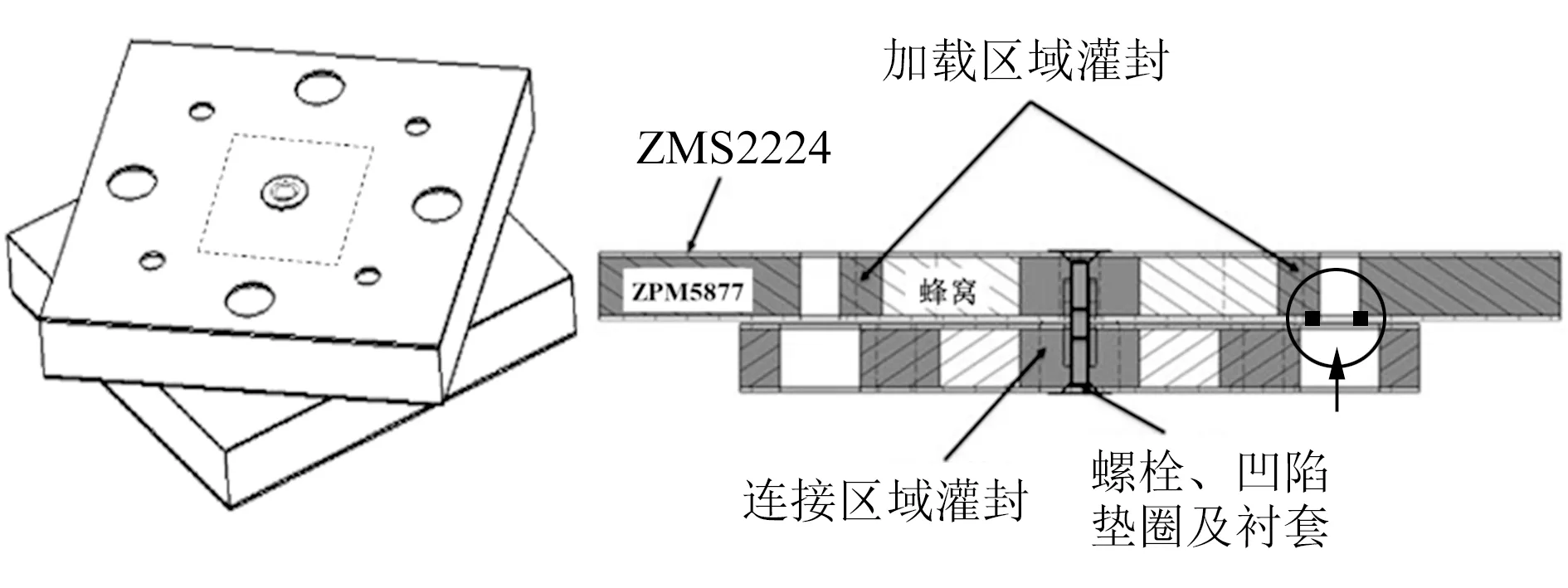
图1 实验件装配图
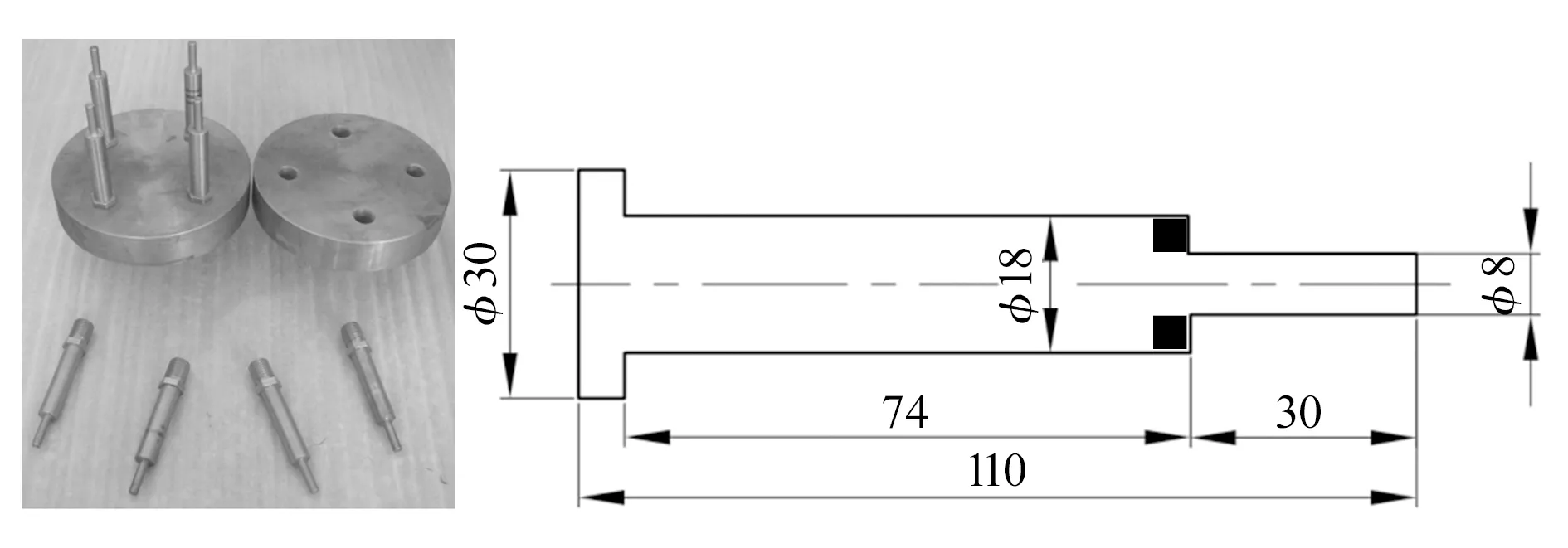
图2 实验卡具及台阶销尺寸
拉伸实验机型号为CSS-2205,如图3所示,实验时沿垂直于蜂窝夹芯结构面板方向加载位移载荷直至实验件拉脱失效。位移载荷的加载速率为0.2 mm/min,上端的载荷通过台阶销传递给下壁板,下端的载荷通过台阶销传递给上壁板,使得连接蜂窝夹芯板的螺栓承受拉伸载荷。

图3 实验装置
1.2 实验结果
图4所示为一组实验件在拉拔载荷下得到的载荷-位移曲线图,由图可以看出,曲线的变化趋势基本一致,且可分为3个阶段:第一阶段为结构初始承载区域,载荷随位移呈线性增长,结构的刚度约为1.2 kN/mm(由图4中的载荷和位移计算得到的均值),直到出现第一个转折点,此时失效载荷约为3 kN,位移约为2.5 mm,实验件已经出现局部破坏,在曲线的第一个转折点处有一小段较为平缓的区域,在此阶段整个结构的刚度重新进行匹配,实验件进入主要承载区,此时刚度约为0.95 kN/mm,实验件刚度下降,但仍有很大的承载潜力,直到曲线的最高点,即极限载荷约为8.5 kN,对应的位移约为8.3 mm,此时实验件进入第三阶段,已经彻底失效,不能继续承载,曲线急剧下降。
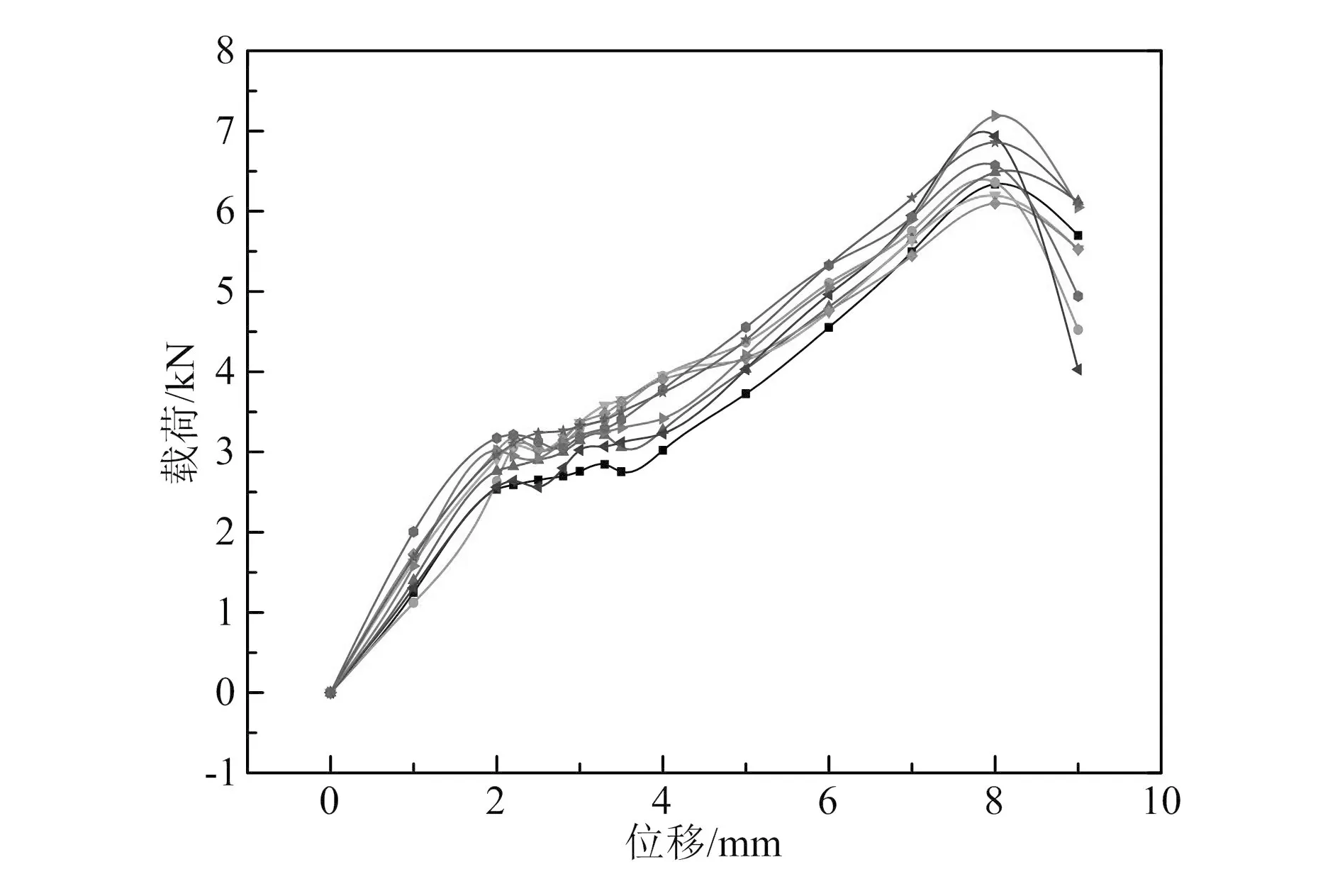
图4 实验件载荷-位移曲线
对实验件进行加载直到其彻底失效,其主要的失效情况如图5所示。由图可以看出,实验件失效后连接件已经陷入面板中,且面板出现了不同程度的损坏,垫圈也出现了裂纹甚至断裂,实验件的失效主要集中在连接区域及其周围。

图5 实验件失效破坏情况
图6为下壁板在载荷小于失效载荷时的变形示意图,下壁板受到上面卡具台阶销向下的作用力,螺栓连接件在上壁板的作用力下牵引下壁板向上运动,因此实验件在螺栓连接区域发生向上的形变,随着载荷的继续增加,螺栓连接件继续向上,直到垫圈陷入到面板中,面板发生不可逆的损坏,实验件失去承载能力,如图7所示。为了进一步了解螺栓连接区域的变形及失效情况,取螺栓连接件附近的A、B、C点作为研究对象,三点的位置分布如图6及图7所示,其中A点接近连接件,C点接近灌封胶填充的边缘,B点则位于A、C两点之间。三点的应变随位移、载荷的变化情况如图8所示,由图可见,在位移-载荷线性变化的初始阶段,A点因距离螺栓连接件较近,垫圈挤压附近的面板,因此A点的应变为负,且随着载荷的增加持续受压;C点离连接区域较远,在受载的初始阶段被拉伸,因此应变为正;B点在A、C两点之间,初始阶段应变不明显。当载荷-位移曲线的第一段结束时,连接区域附近的基体逐渐被压溃,A点由受压转为受拉,B点和C点继续受拉,应变的变化趋势变缓,直到载荷达到极限载荷时,三点的应变较大,此时结构已经失效,A点彻底被破坏。

图6 下壁板变形示意图(载荷小于失效载荷)

图7 下壁板变形示意图(载荷达到失效载荷)
2 数值仿真
2.1 蜂窝夹芯结构的等效模型
本文采用三明治夹心等效模型理论[5],将整个蜂窝夹芯板等效为一块正交各向异性的板,其对应的等效弹性参数为:
(1)
式中:Ecx,Ecy,Ecz分别为x,y,z方向的弹性模量,c为等效后的参数;Gcxy,Gcxz,Gcyz分别为对应方向的剪切模量;μs,Es,Gs分别为蜂窝夹芯结构密度、弹性模量以及剪切模量,s为等效前蜂窝芯的工程常数;l为蜂窝单胞的外接圆半径;t为蜂窝芯的壁面厚度;γ为修正参数,取值为0.4~0.6。
2.2 破坏准则
本文的破坏准则采用“扩展Hashin准则”[6],当e2>1时认为材料发生了不可逆的破坏。其主要破坏模式及刚度衰减见表1。

表1 Hashin失效准则及对应的刚度衰减
2.3 有限元模型
在ANASYS中建立复合材料蜂窝夹芯结构实验件的有限元模型,蜂窝夹芯板的上下壁板为复合材料层合板,铺层为[45/0/45/]S[45]3,材料为ZMS2224,计算时采用SOLSH190单元;蜂窝夹芯板中间的NOMEX蜂窝(3型2类A级)材料为ZMS1974;蜂窝空腔的填充灌封料为ZPM5877,计算时采用SOLID185单元。
2.4 数值计算结果
图9所示为数值仿真计算得到的实验件载荷-位移曲线图,由图可以看出,整个曲线非常平滑,并没有出现实验数据图中明显的转折点,这是因为对计算模型作了简化处理,如理想加载、理想连接、0-1退化等等,但曲线仍模拟出了蜂窝夹芯板在拉拔载荷下的载荷-位移变化趋势,曲线在第一段也呈线性变化,随着载荷的进一步增加,曲线斜率减小,刚度降低,直至达到结构的极限载荷。数值仿真计算得到结构的极限载荷约为5.9 kN,实验得到结构的极限载荷的平均值约为6.5 kN,计算结果小于实验数据,误差在10%以内,本文采用的计算模型得到的计算结果较安全。若能有更多的相关数据,则可以通过实验值和计算值的比较得到安全系数,从而可以对结构的承载能力进行准确的预测。在工程实际中进行设计或者结构优化时,往往需要快速知道结构的承载能力,此时可以通过数值计算进行准确的预判。
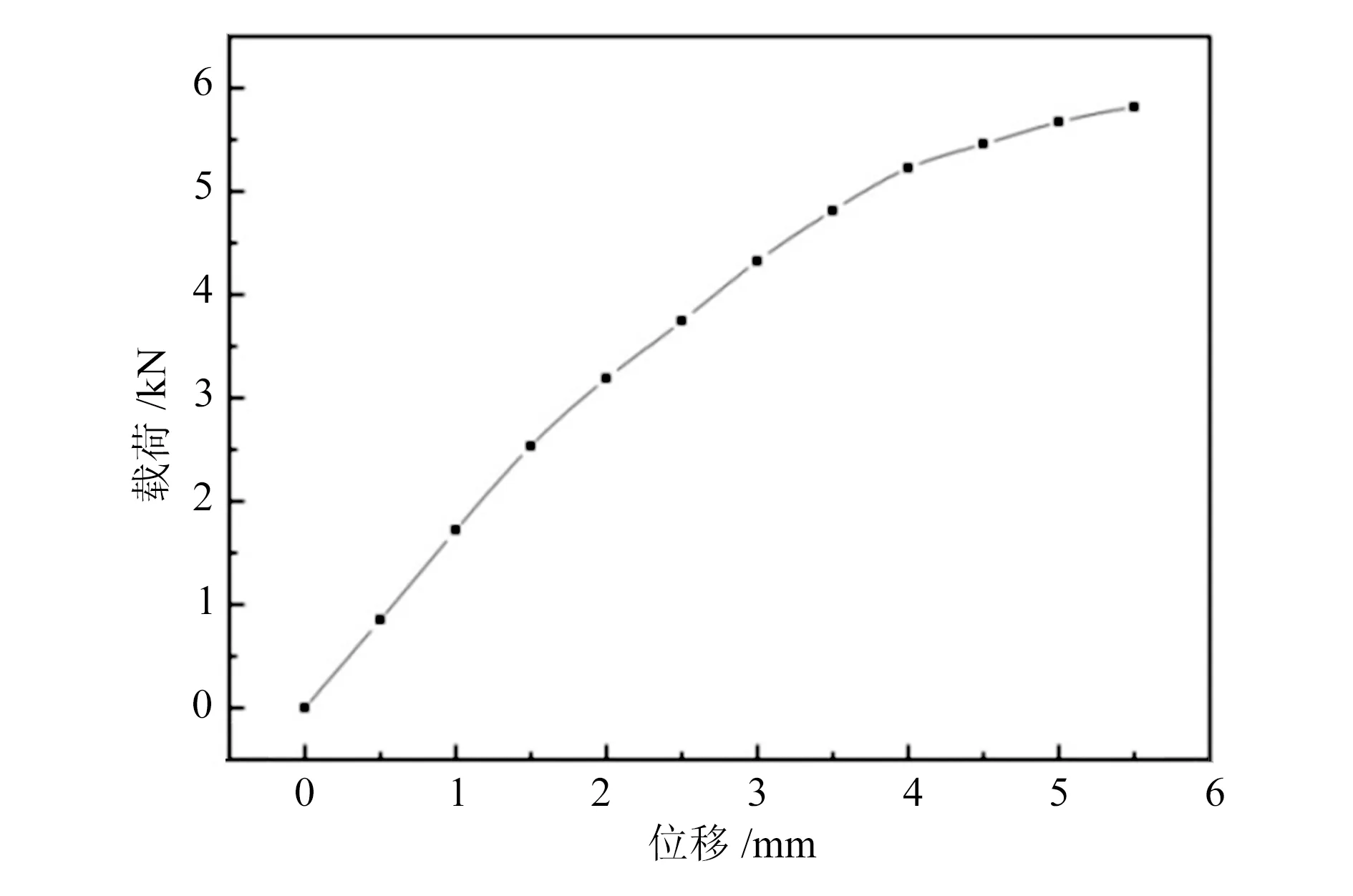
图9 数值仿真计算载荷-位移曲线
3 结论
本文对复合材料蜂窝夹芯结构进行拉拔实验以及有限元数值模拟计算,得到以下结论:
1)蜂窝夹芯结构在拉拔载荷的作用下,失效的主要区域集中在连接件周围,多以垫圈凹陷、面板损坏的形式出现;
2)本文建立的数值仿真模型计算得到的承载能力小于实验值,且误差不到10%,较安全,对蜂窝夹芯结构承载能力的预测有实用价值。

