面向线上-线下异步社会网络的病毒式营销算法

王长军， 王葛格， 2

(1.东华大学 旭日工商管理学院，上海 200051; 2.杭州百世网络技术有限公司，浙江 杭州 310013)

现实中，企业常借助口碑(word of mouth， WOM)实现在消费者中的“病毒式”扩散，激发需求，实现经营目标。无论是文献[1]中传统的面对面WOM相关研究，还是文献[2-3]中基于互联网媒体工具的e-WOM(electronic WOM)的相关研究，均验证了信息传播和市场结果间存在的直接联系。因此，基于口碑传播的病毒式营销策略设计变得至关重要。

一般情况下，营销者为部分用户提供免费产品，希望其使用后能在朋友圈中进行宣传，以吸引新用户，并由此将影响扩散开来[4]。Domingos等[5]最早将这一问题归结为网络中的种子节点选取，旨在通过种子节点的社会联系扩散口碑，以影响网络中尽可能多的节点，实现影响最大化(influence maximization， IM)。IM问题的提出引发了研究者们广泛的研究兴趣，但目前相关研究大多针对单层社交网络展开，故仅考虑了单种口碑[6]。实际中，面对面传播的WOM和e-WOM同时存在，两者分别依托线下和线上社会网络，且网络结构和传播速度也不同，通常线上传播速度快于线下[7]。针对这一双层异步网络，如何设计病毒式营销策略以实现IM，成为决策者面临的核心问题。

现有文献在研究基于网络的IM问题时关注两个重点：一是构建口碑在网络中各节点间的扩散机理；二是基于该机理选择设计营销策略，即选取口碑扩散的源头(种子节点)。前者根据口碑扩散过程是确定的还是随机的，将口碑扩散模型分为确定型[8]和不确定型两类。后者由于能够描述传播过程中的随机性而广受关注，其中最常见的是独立级联(independent cascade， IC)模型[9-12]。IC模型中，一个已被成功影响(又称激活)的节点会以一定的概率影响其未被激活的邻居，由此进行传播。继而，大量研究关注了基于IC模型的种子节点选取。

Kempe等[9]较早深入研究了基于IC模型的IM问题，证明最优的种子节点选择为NP-hard，并设计了选取种子节点的贪婪算法，利用函数的次模性证明了算法具有1-1的性能界，仿真结果也表明贪婪算法的表现优于传统的出度规则和随机选择规则。但是，贪婪算法中的遍历操作致使其时间复杂度很高，对于稍大的社交网络存在伸缩性的缺点[13]。Leskovec等[14]利用目标函数次模性对贪婪算法进行改进，减少每次选择初始种子节点的计算量，由此提出CELF(cost-effective lazy forward)算法。CELF算法运算速度较经典的贪婪算法有显著提高，但仍难以应用于大规模网络[15]。王长军等[16]构建基于IC模型的马尔科夫模型，采用贪婪算法进行种子节点的选取研究，但也只能针对小规模网络进行仿真。

由于贪婪算法及其扩展算法存在问题，因此更多文献考虑设计启发式算法解决基于IC模型的IM问题。典型的如Chen等[15]提出的Single Discount算法和Degree Discount算法。这两种算法都是基于“度(degree)”的算法，为避免邻近的种子节点影响的重叠，两者在度折算上采用不同的方式。仿真结果显示，以上两种算法在计算时间和效果上较出度规则和CELF算法都有着更为优异的综合表现。Estevez等[17]考虑节点在网络中的位置，提出集合覆盖贪婪(set covering greedy， SCG)算法，以避免同一社团中的种子节点被选中，从而获得影响的最大程度扩散，仿真表明该算法较出度规则和贪婪算法更为有效。然而，这些工作都是基于单层网络。

近年来，有研究[7， 18-19]注意到多层网络下的IM问题的重要性，并指出这是一个新的、快速发展的领域，但多数研究仅考虑多层线上网络(如推特、Facebook)的信息传播[13]。由于网络特性相似，故而研究要么单独对每层建模，再将每层影响直接叠加(如Erlandsson等[20])，要么将多层网络缩减为单层网络予以研究(如Zhang等[21])。这就忽略了不同层级网络下WOM和e-WOM传播可能具有的不同特性，如传播异步性等[7， 22]。现有工作也未研究适用于单层网络的启发式算法是否能扩展至多层网络这一问题。显然，设计高效启发式算法对解决现实中的大规模双层网络下的IM问题是至关重要的[6]。

综上，本文扩展经典IC模型以描述影响WOM和e-WOM在双层社交网络下的病毒式传播，并对经典的启发式算法(包括Single Discount、 Degree Discount和SCG算法等)进行改造，解决双层网络下IM问题中的营销策略设计问题，通过仿真对比分析其营销结果。本文创新点：一是扩展了经典IC模型，构建适用于双层异步网络IM模型；二是设计可求解大规模情境下这一问题的启发式算法；三是无论是模型构建还是算法设计，都考虑了WOM和e-WOM所依托的网络结构和传播速度的不同。

1 模型构建

依托双层的线下和线上网络，WOM和e-WOM分别进行传播，并考虑传播的不同步性。考虑现实情境，假设WOM传播慢于e-WOM。为此，引入变量ξ(∈N+)，设定e-WOM在上层网络中每周期传播1次，而WOM每ξ个周期才传播1次。为反映当前时刻t是否存在WOM传播，引入0～1变量λ(t)，如式(1)所示。

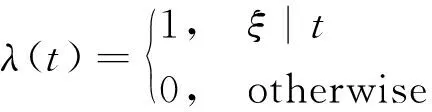
(1)

式中：ξ|t表明t为ξ整数倍，λ(t)取1，表示WOM传播也可起作用，反之，λ(t)为0，此时信息仅通过上层网络传播。

将经典IC模型扩展至双层相依网络的关键在于，网络中任一节点如何处理来自于某邻居节点由不同传播途径传递的信息的问题。注意到文献[23，25]在相依网络研究中对来自不同层级网络的影响做叠加处理，可以理解为现实社交网络中的人会受到WOM和e-WOM的叠加影响。基于这一想法，同时考虑λ(t)的存在，对IC模型进行扩展，则在t时刻，节点vi被vj激活的概率pij(t)可表述为式(2)。

(2)

该动态扩散过程始于种子节点的选取，即需从节点集合V中最多选取k(≤N)个节点，构成种子节点集合，定义为S，作为影响扩散的起点。另记最终被激活节点集合为δ(S)。假设决策者掌握准确的双层相依网络(V，Ez)信息，由此相应的IM问题如式(3)所示。

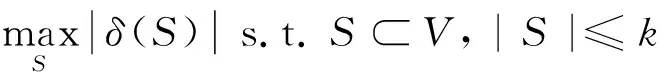
(3)

Kempe等[9]证明单层网络下IM问题为NP-hard。显然，对于大规模网络，求解问题的精确解是困难的。为此，本文关注高效的启发式算法的设计。

2 病毒式营销中的种子节点选取算法设计

现有研究设计的Single Discount算法、Degree Discount算法和SCG算法已被成功应用于单层网络，此处将3种算法进行扩展，以使其适用于上文的双层相依网络下的IM问题。

2.1 扩展Single Discount算法

输入：(V，Ez) (z={u，l})，k和ξ

输出：集合S

1：INITIALIZES=φ，N=|V|

2：FORi=1 toNDO

4：ENDFOR

5：FORt=1 tokDO

6： 找到vi=argmaxvi∈VShi(ξ)，更新S=S∪{vi}

7：FORvj∈VSDO

8：COMPUTEhj(ξ)=hj(ξ)-

10：ENDFOR

11：ENDFOR

12：OUTPUTS

2.2 扩展Degree Discount算法

输入：(V，Ez)(z={u，l})，k和ξ

输出：集合S

1：INITIALIZES=φ，N=|V|

2：FORi=1 toNDO

5：ENDFOR

6：FORt=1 tokDO

11：ENDFOR

12：ENDFOR

13：OUTPUTS

注意到以上算法的第10步中为修正vj的影响程度，故要判断当vi被选作种子节点时对它的影响，因此，式中采用的是pji(t)而非pij(t)。

2.3 扩展SCG-d算法

输入：(V，Ez)(z={u，l})，k、ξ和d

输出： 集合S

1：INITIALIZES=φ，N=|V|

2：FORv=1 toNDO

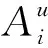
4：ENDFOR

5：FORt=1 tokDO

6： 找到vi=argmaxvi∈VShi(ξ)，

8：ENDFOR

9：OUTPUTS

3 试验与分析

基于扩展IC模型，利用所提的3种启发式算法和传统的Max Degree规则(即直接选取出度hi(ξ)最大的节点)与Random规则(即随机选取种子节点)求解双层相依网络IM问题，观察对比各自的营销结果。

3.1 试验设置

以人际间的线下和线上网络为背景，构建仿真所需的双层相依网络。注意到线下人际关系满足“六度分离”，具有典型的小世界特征[26]，而线上网络不仅具有小世界特征，其“度”还服从幂律分布，符合无标度网络[27]，故分别采用这两个网络构建仿真所需的线下和线上网络，这一做法与文献[3，22]一致。

小世界模型的构造算法[26]：(1)构建规则网络。给定一含有I个点的环状最近邻耦合网络，每个节点都与它左右相邻的各Q/2个节点相连，其中Q为偶数。(2)随机化连边。随机重新连接网络中原有边，即保持每条边的一端点不变，而将另一端点改为连接至随机选择的一个节点，但不能有重边和自环。

无标度模型的构造方法[27]：(1)增长。建立一个具有m0个节点的连通网络，每次引入一新节点并且连到网络中m(≤m0)个节点上。(2)优先连接。新节点会优先与网络中连接度大的节点相连。

将从传播概率、网络结构、WOM/e-WOM传播异步程度3等方面进行仿真试验。其中，网络节点数为10 000，种子节点数量k的取值规模取值为[5～50]。定义影响扩散比例(influence diffusion ratio， IDR)为IDR=|δ(S)|/N，即用激活节点数占网络总节点比例来衡量营销结果。为避免扩散模型的随机性带来的干扰，每组参数重复计算10次，将IDR均值作为仿真结果。

所有试验均在配有Windows 10 64位操作系统、主频为4.00 GHz、内存为32 GB的台式电脑上运行，编程采用C语言。

3.2 基于不同影响传播概率的试验与分析

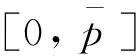
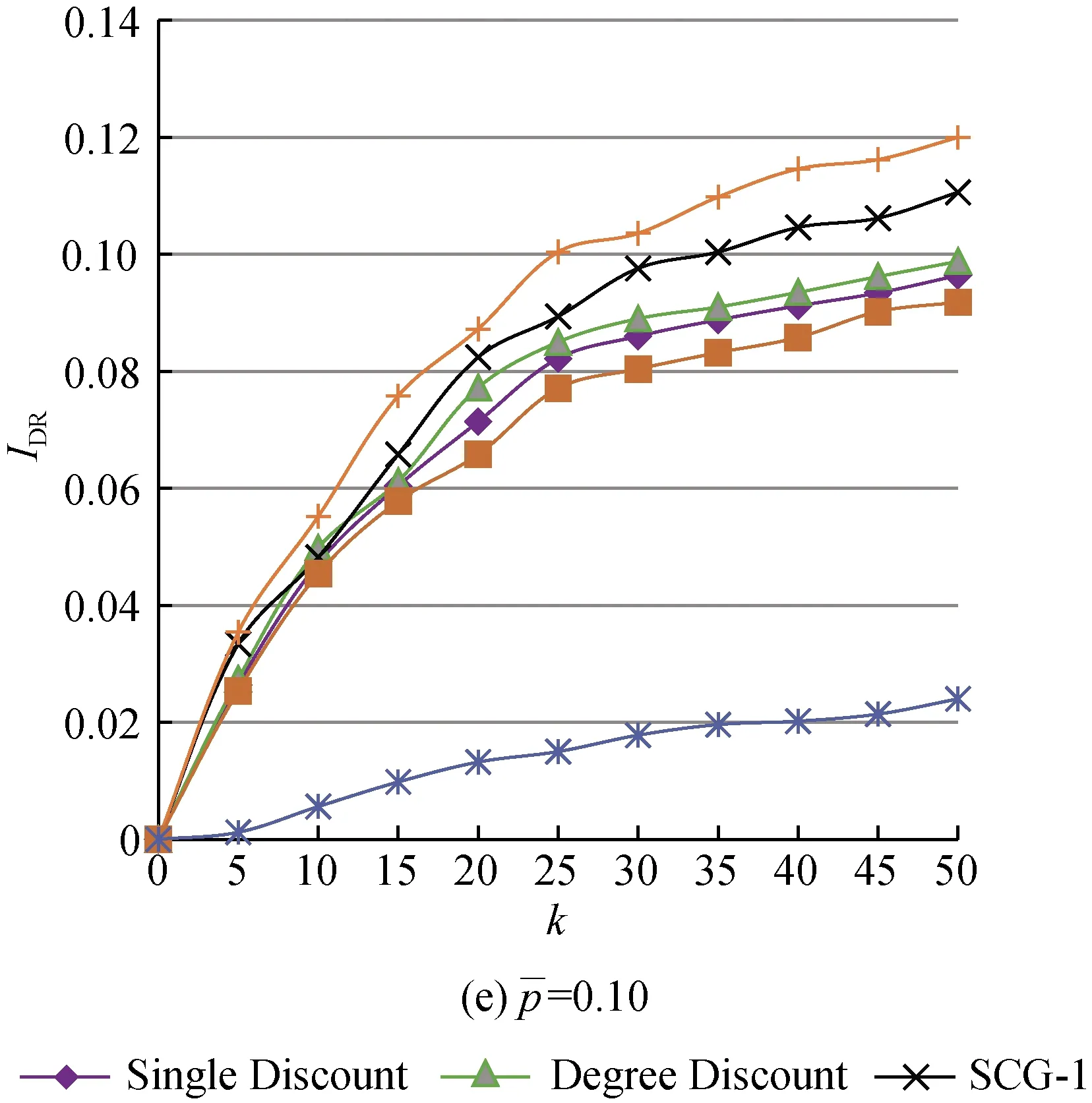
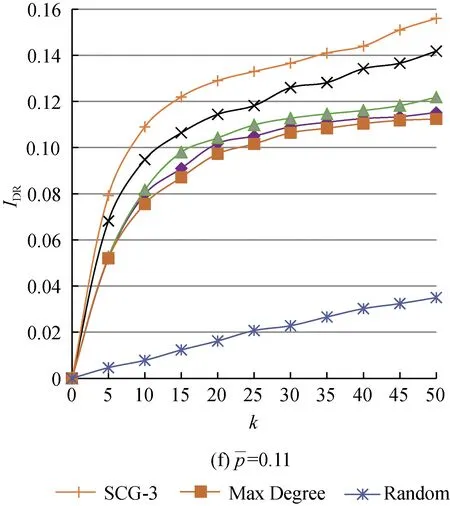
图1 不同值下的仿真结果

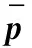
表1 不同下SCG-3与其他算法IDR的差异Table 1 IDR difference between SCG-3 and other algorithms under different %

由图1和表1可得出以下结果：

(1) 随着激活概率的增大，各算法的IDR都呈上升趋势。这是因为口碑在传播能力强的网络中的扩散范围必然大于传播能力弱的网络。Single Discount、 Degree Discount和Max Degree算法的效果较为接近，这是因为从根本上它们都是基于节点出度做选择的。

(3) SCG-3始终优于SCG-1，这是因为SCG-3考虑了更大的邻域，减少种子节点的聚集情况，使传播更为快速有效。

表2给出了k=50下的平均计算时间。不难发现，随机算法的耗时最短，Max Degree只需计算一次所有节点的出度，耗时次之。SCG-1节省了节点出度更新的步骤，但需给出邻域；SCG-3需要在更大的领域中搜索，耗时最长。但考虑到此处网络规模为10 000个节点，不同算法的计算耗时都是可以接受的。

表2 k=50不同算法的平均运行时间Table 2 Calculation time of different algorithms when k=50 s

3.3 基于不同网络结构的试验与分析

选取4种不同的(Q，m，m0)组合，分别为Ⅰ=(4， 5， 5)、Ⅱ=(6， 7， 7)、Ⅲ=(8， 9， 9)、Ⅳ=(10， 11， 11)，用以表达不同的双层网络结构。节点间激活概率服从[0， 0.1]之间的均匀分布，ξ=1。

仿真结果见表3和图2。结果表明：随着网络间连接的增加，各算法IDR逐渐改善。这是因为网络中边的数量和节点平均出度增大，利于WOM和e-WOM的扩散。随网络间节点连接的加强，SCG-1和SCG-3的所得结果改善明显。这是因为节点间的邻居节点重叠率在上升，激活行为重叠的现象也愈加明显，而SCG算法能够削弱种子节点重叠的概率并使之分布相对分散。各算法计算耗时与第3.2节结果相近，此处不再赘述。

表3 不同网络结构下SCG-3与其他算法的IDR差异Table 3 IDR difference between SCG-3 and other algorithms under different network structures %

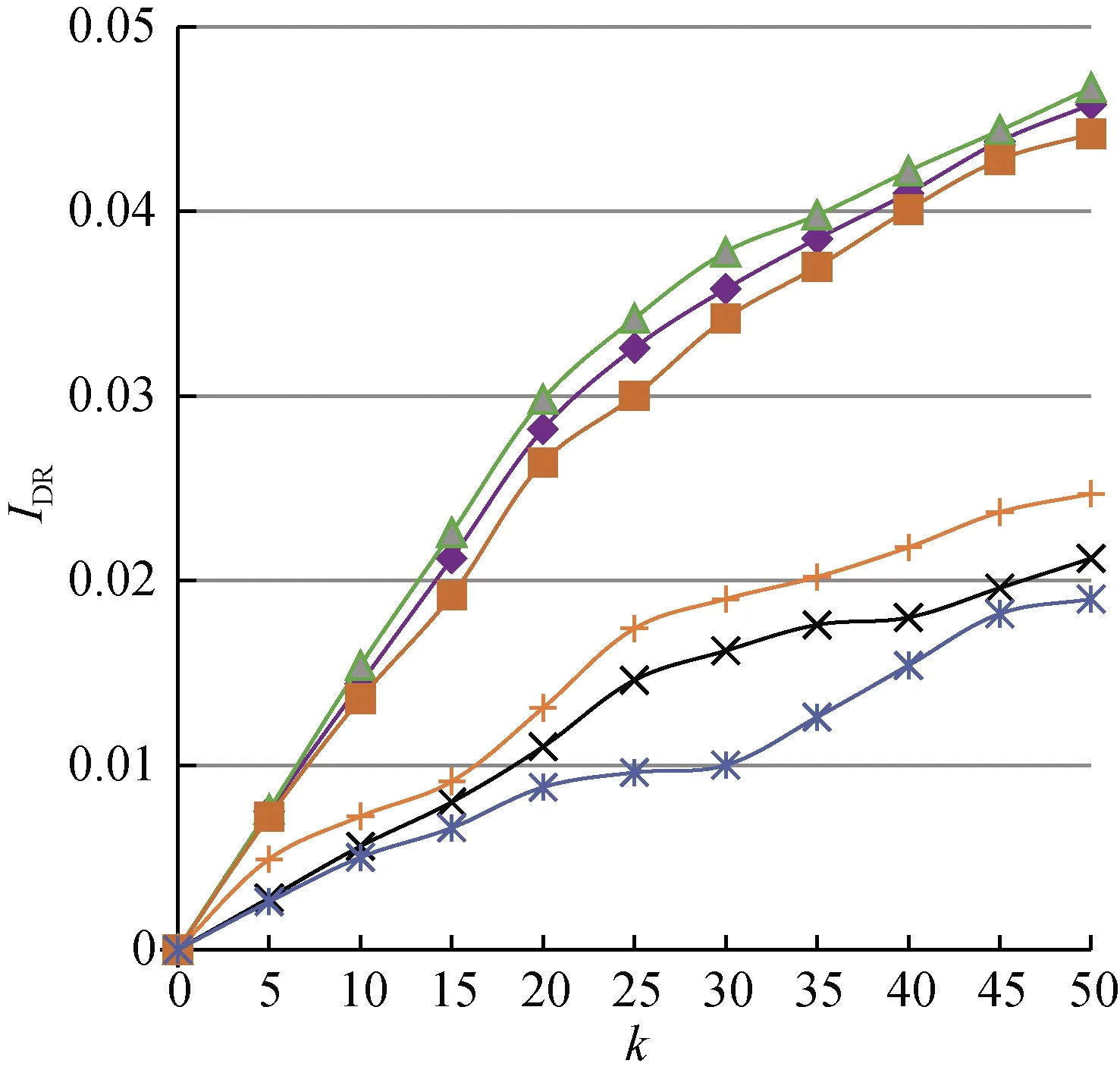
(a) 网络结构Ⅰ

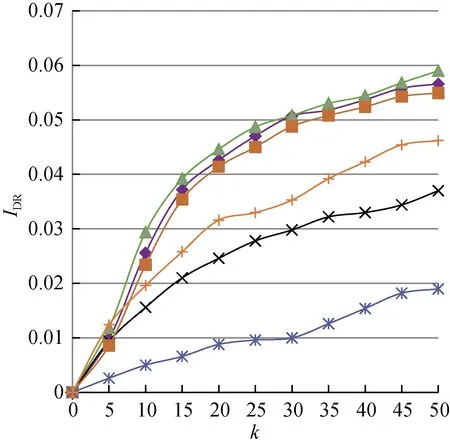
(b) 网络结构Ⅱ

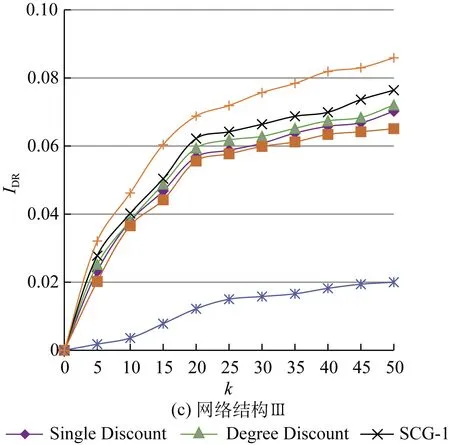
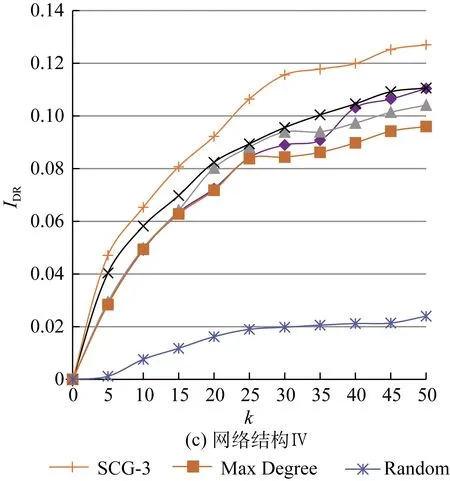
图2 不同网络结构下的仿真结果

3.4 基于WOM/e-WOM异步程度的试验与分析

研究不同传播异质程度下的营销结果，取ξ={2， 4， 6， 8}，Q=10，m=10，m0=10。双层网络中各节点间激活概率服从[0， 0.1]的均匀分布。

观察差异化网络传播异步程度时SCG与其他算法的IDR百分比差异(见表4)和IDR变化情况(见图3)，可以得出：随着WOM/e-WOM传播异步程度的增加，式(2)中λ=1的情形越来越少，节点间的总体激活概率减小，导致各方法的营销结果普遍变差。此外，在这一网络结构下，无论ξ取何值，SCG算法的结果始终稳定地优于Single Discount、 Degree Discount以及Max Degree等基于度的算法。

表4 差异化WOM/e-WOM传播异步程度时SCG-3算法与其他算法的IDR差异Table 4 IDR difference between SCG-3 and other algorithms under different asynchronous extents of WOM/e-WOM diffusion %

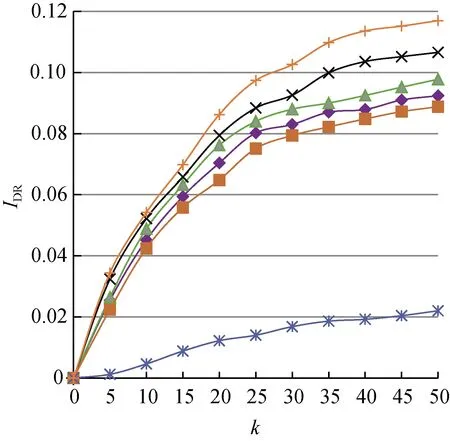
(a) ξ=2

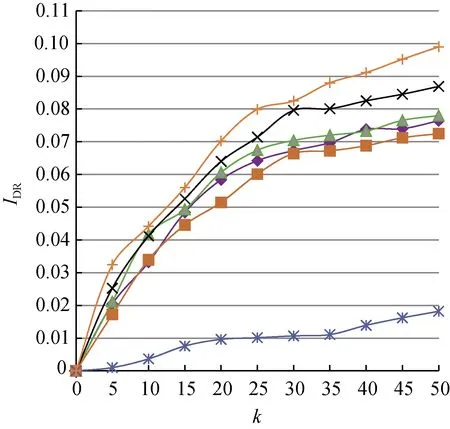
(b) ξ=4

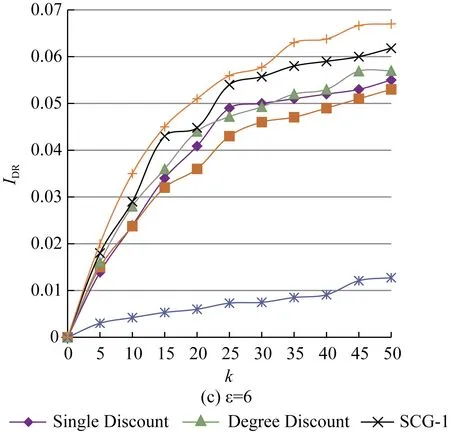
(c) ξ=6

(d) ξ=8

4 结 语

基于口碑的病毒式传播已成为企业获取需求的重要方式。在复杂的商业环境中，口碑以不同形式结合不同的途径进行传播，典型的则是面对面的传统口碑和基于互联网媒介的数字化口碑的共存。研究面向双层异步网络病毒式口碑营销策略，扩展经典独立级联模型，构建相应的影响最大化模型，并将单层网络下的典型种子节点选取算法扩展到双层相依网络下，以解决营销策略的制定问题。结果表明：所设计的基于度的算法和集合覆盖算法明显优于传统的随机规则和最大度规则，揭示不同算法对于不同传播概率以及网络结构情境的适用性，同时发现传播异步性对于以上算法的营销效果的负面影响。此外，包括消费者规模、网络结构、口碑传播概率以及异步性等在内的市场信息，对于成功展开病毒式营销、预测营销结果是至关重要的。显然，这一问题的研究和相关结论对于身处复杂信息传播环境的企业营销决策有着重要意义。

后续研究可从3个方面展开：(1)在口碑方面，仅考虑了2种不同的口碑形式，而未考虑口碑的内容，关于正负口碑的研究已不鲜见，但在双层网络上考虑口碑的正负性还有待进一步研究。(2)本文揭示传播概率和网络结构等因素对于营销效果的影响，可以继而考虑双层网络中不同影响概率分布以及人群的社团效应，设计更有针对性的种子节点选取方法，以解决复杂场景下的现实问题。(3)本文假设决策者掌握准确的网络结构信息，这对于线上网络是可能的，但对于线下人际关系网络并不容易。因此，如何在网络信息有限的情况下进行病毒式营销也是未来一个重要的研究问题。