CAES轴流涡轮弯导叶优化设计与流动损失控制机理

王 星 ，李文 ，朱阳历 ，左志涛 ，陈海生 ,4

（1中国科学院工程热物理研究所，北京 100190；2中国科学院大学，北京 100049；3毕节高新技术产业开发区国家能源大规模物理储能技术研发中心，贵州 毕节 551712；4中科南京未来能源系统研究院，江苏 南京 211135）

压缩空气储能(CAES)系统是实现电力调峰、克服风能和太阳能不稳定性的重要技术。上述优点使该系统被广泛应用于现代电网[1]、可再生能源[2]、余热利用[3]、多能联产[4-5]等领域。

轴流涡轮是CAES系统中重要做功装置，对系统性能有重要影响[6]。由于该涡轮常在高总压、低温度工况下运行，因此该类涡轮导叶具有低展弦比的结构特点，这种结构特点会使轮毂和机匣附近端壁二次流的影响程度提高并增加轴流涡轮内部流动损失。

弯叶片是改善轴流涡轮端壁流动的关键技术之一，对提高效率有重要作用[6]。随着加工技术的不断进步，弯叶片在叶轮机械上的应用可行性增加，因此近几年有不少学者在这方面开展了广泛研究。Zhao等[7]对低压涡轮级进行了弯导叶优化设计，结果表明，当采用正弯导叶且弯角为18°时，涡轮性能最优，并且弯导叶能够通过改善出口气流角实现对端壁二次流的控制。韩俊等[8]采用数值模拟方法对小展弦比涡轮叶片进行了弯曲造型优化设计。通过对比分析不同方案的膨胀比和流量，发现反弯设计要优于正弯和直叶片设计，且反弯15°方案最优。陈雷等[9]采用数值模拟方法研究了弯导叶设计对两级涡轮性能的影响，结果发现采用第1级静叶反弯、第2级静叶正弯的结构形式能够使涡轮气动绝热效率相对最优，且J形弯曲造型设计更能改善负荷分配，并降低二次流损失和激波损失。隋秀明等[10]将叶片弯曲造型方法引入氦工质涡轮中，研究叶片弯曲造型参数对高负荷低展弦比涡轮端壁损失的影响机理。结果表明：叶片正弯会使叶顶负荷减小，显著降低叶顶间隙泄漏涡与通道涡强度及损失，使涡轮性能得到改善。Yao等[11]研究了新型S弯导叶对1台超声速工业汽轮机气动性能的影响，结果表明，该叶片能够提高超音速涡轮的效率，导叶的能量损失系数可降低2.4%以上，在变工况条件下，能量损失系数减小幅度更高。

随着叶轮机械理论和技术的不断进步，又有学者将其他流动控制方法与弯叶片相结合，以进一步改善气动性能。Zhang等[13]将反弯叶片与非定常脉冲抽吸孔结构相耦合以提升高负荷压气机的气动性能和效率。结果表明，当反弯角为10°时，总压损失系数可降低24%。Guo等[13]将弯叶片造型和端壁非轴对称设计相结合，采用实验方法，研究了对涡轮叶栅气动性能的影响。研究结果表明，弯叶片和端壁非轴对称造型的耦合能够有效减小低展弦比叶栅的二次流影响面积和叶型损失。

除气动性能方面外，弯叶片设计在控制涡轮非定常气流激振力方面也能带来有益效果。杨彤等[14]开展了弯曲叶片造型对涡轮叶栅非定常作用力影响的数值研究。结果表明：正弯曲造型能够通过改变静叶出口处径向压力梯度和涡量分布实现动静叶片表面气动力的非定常脉动的有效抑制。刘建等[15]对不同倾斜/弯曲导叶构型的跨声速涡轮级进行全三维黏性非定常数值模拟，研究了倾斜/弯曲导叶对涡轮级效率及效率波动影响，结果表明：正倾斜和正弯曲导叶通过降低不同阶转子叶片扰动强度可减低转子叶片扰动，并可以有效提升涡轮级效率。

然而弯叶片对轴流涡轮气动性能改善效果也会存在局限。Tan等[17]在对某一涡轮导叶进行弯曲造型设计研究中发现，正弯造型既不能减小叶栅两端壁附近的损失，也不能使出口气流偏转角分布更加均匀，并指出需要仔细考虑尾缘的影响。

以上研究结果表明，弯叶片的造型会对气动性能产生复杂影响，需要结合具体的导叶进行研究和分析。另一方面，在空气储能涡轮领域，弯导叶设计对轴流涡轮影响研究较少，关于弯导叶参数对涡轮等熵效率和质量流量影响规律探索也存在不足。

综上所述，以弯高和弯曲角为自变量，以等熵效率为优化目标，通过CFD模型获得样本点数据集并构建响应面模型，并以此采用遗传算法开展了压缩空气轴流涡轮弯导叶优化设计，使轴流涡轮等熵效率进一步提升，并进一步分析了最优弯导叶对流动损失的影响机理。

1 研究对象

选取10 MW压缩空气储能系统中高压级轴流涡轮做为研究对象。见表1，该级涡轮运行压力较高，导叶平均叶高与弦长之比约为50%(表2)。上述结构特点使端壁二次流体在导叶通道内发展过程较长，影响范围较大。出于加工要求，导叶叶根和叶顶还有倒角结构，进一步对端壁附近流动产生复杂影响，轴流涡轮整体结构如图1所示。

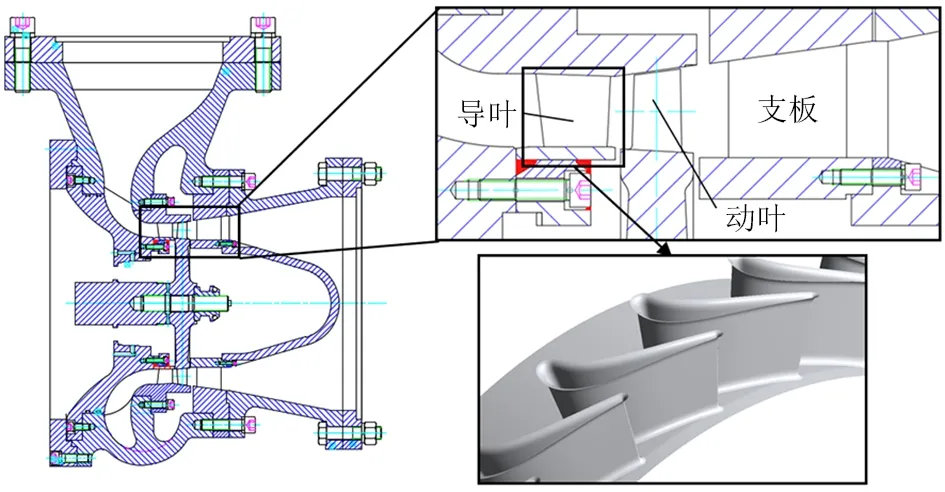
图1 本文轴流涡轮几何结构Fig.1 Geometry of axial turbine in present study

表1 本文轴流涡轮的运行工况参数Table 1 Operation condition parameters of axial turbine in present study

表2 原导叶主要几何参数Table 2 Geometric parameters of original vane

2 研究方法

2.1 低展弦比弯导叶造型方法

上述结构特点表明导叶端壁二次流是影响本文轴流涡轮流动损失的主要因素之一。已有研究结果表明，J形弯叶片结构对叶根部附近局部压力场和流场分布有显著影响[17]，因此本文引入J形弯叶片结构并开展研究。图2为J形弯叶片参数模型，如图所示，叶片的弯曲造型主要通过叶根弯角α1、弯高C1以及弯曲线控制点相对高度P1实现，叶顶部分则不做弯曲造型处理。本文主要以叶根弯角α1、弯高C1为变量开展研究，保持P1值不变。图中各参数的取值范围见表3。

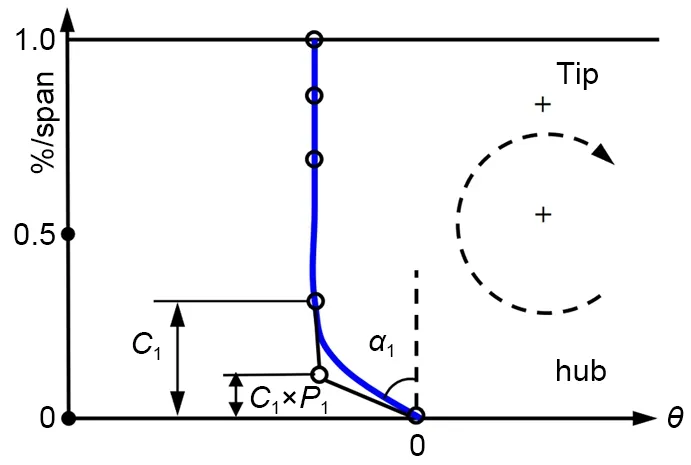
图2 J形弯叶片参数模型Fig.2 Parameter model of“J”-type bowed vane

表3 本文弯叶片参数取值范围Table 3 Range of bowed vane parameters in present study

2.2 轴流涡轮三维流场数值求解方法

2.2.1 数值模型

本文采用全三维计算流体动力学(CFD)模型完成轴流涡轮内部流场结构以及等熵效率、流量等气动性能参数的求解，模型详细结构如图3所示。采用单通道流动域建模方法，在进口给定总温、总压边界条件；出口给定静压边界条件，壁面采用无滑移边界，动静交界面采用“stage”类型；湍流模型采用k-ε模型。采用结构化六面体单元对流动域进行离散。总网格单元数在701056个，并对近壁面网格进行加密使第1层网格单元厚度y+满足湍流模型求解要求。

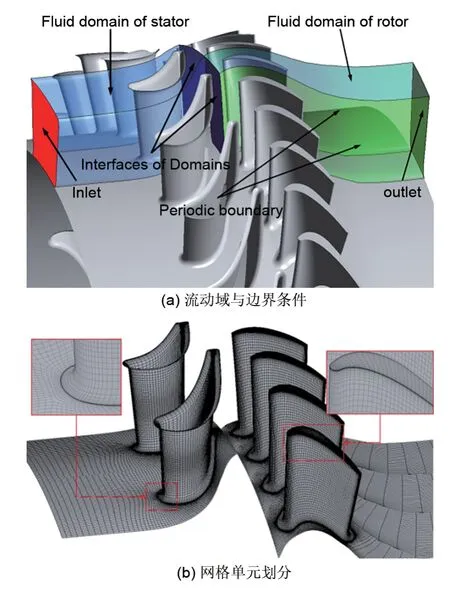
图3 本文CAES涡轮数值计算模型Fig.3 Numerical simulation model of CAES turbine in present study

2.2.2 数值方法验证

本文采用典型Aachen轴流涡轮[18]完成模型验证。图4(a)为Aachen涡轮的几何结构；图4(b)为针对该涡轮建立的数值模型以及相关的网格划分。本文采用与2.2.1 节中相同类型的边界条件、网格单元划分方法、数值求解方法对流场进行求解以验证数值模型精度。

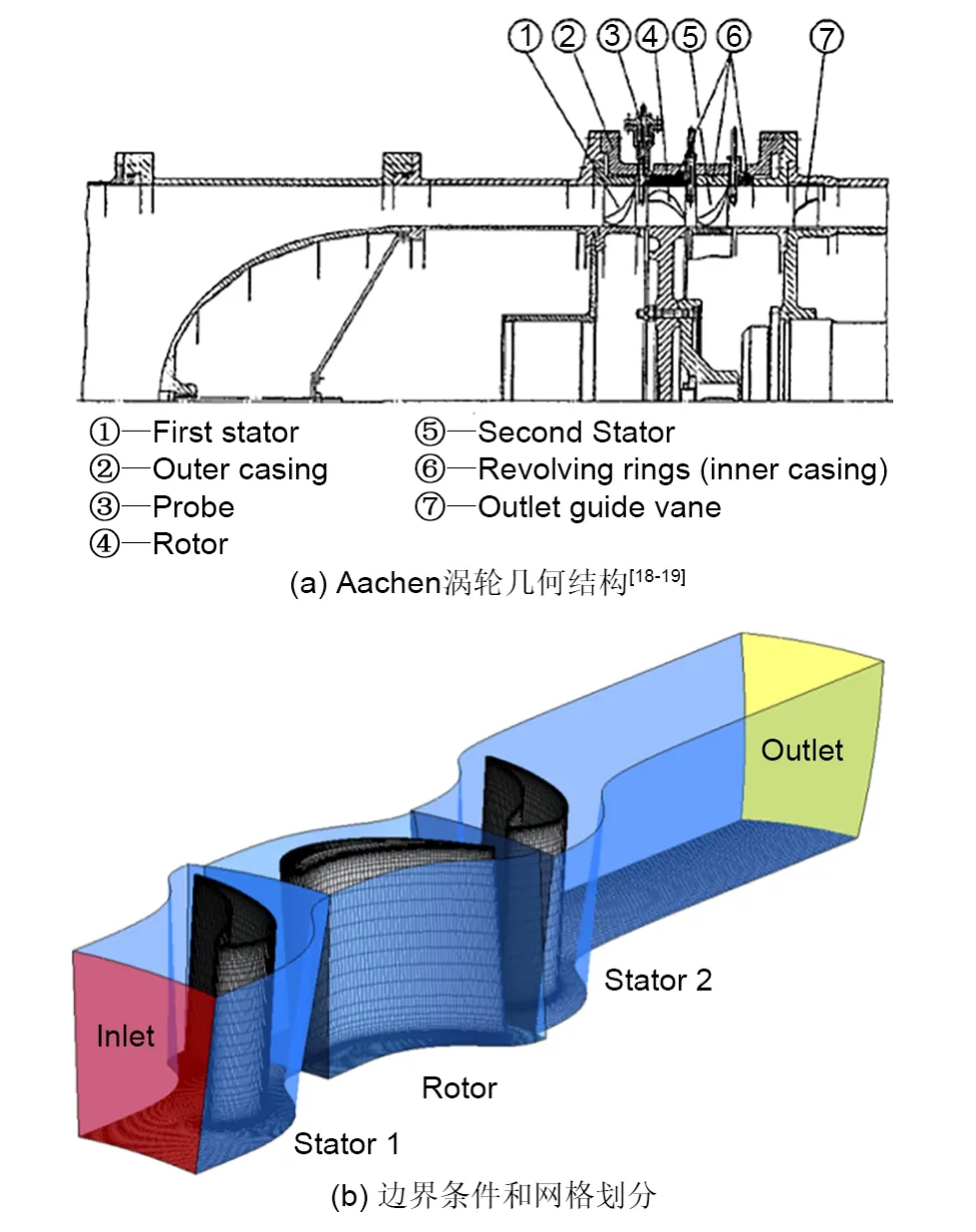
图4 Aachen轴流涡轮数值计算模型Fig.4 Numerical model of Aachen axial turbine

图5为数值模拟与实验结果的对比，如图所示，本研究采用的数值计算模型能够较为准确地预测涡轮内部的流场总压分布。由于数值模型并未考虑实验中存在的动静叶之间的轴向间隙以及轮盘泄漏气的影响，因此在动叶尾缘和第二导叶尾缘区域轮毂附近的流场预测误差较大，但整体分布与实验基本一致。

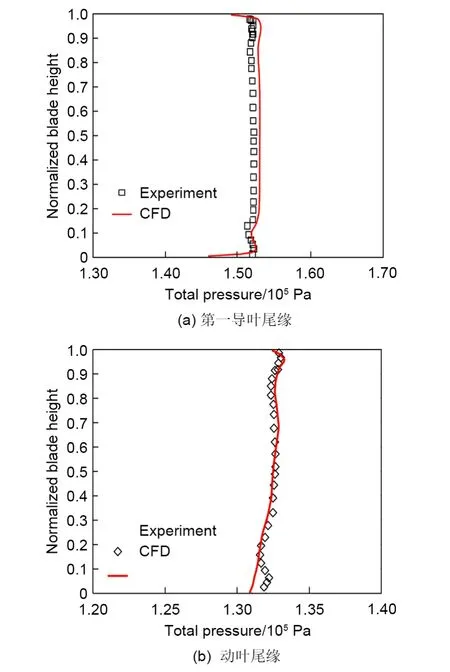
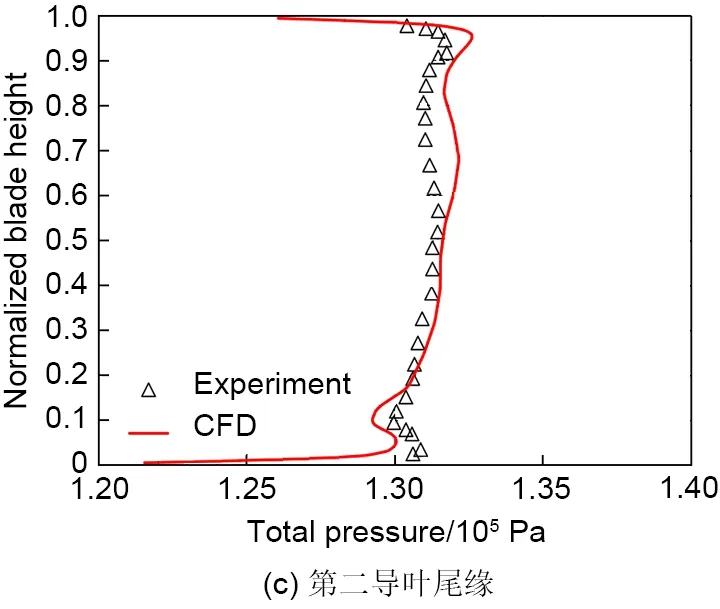
图5 数值模拟模拟方法验证[19]Fig.5 Verification of numerical simulation method

2.3 弯导叶优化设计方法

图6为轴流涡轮弯导叶优化设计流程。首先采用上述轴流涡轮数值模型，对不同弯叶片参数下的涡轮流场进行求解，获得与之相应的等熵效率和流量；其次通过上述结果构建样本点数据集，基于该数据集进一步生成响应面模型；最后以该响应面模型为基础，采用遗传算法进行优化，最终获得最优弯导叶造型。

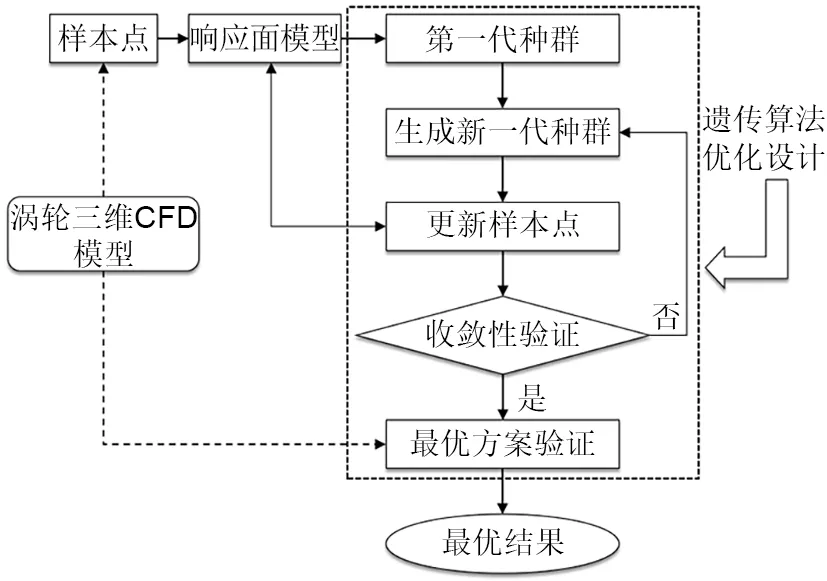
图6 轴流涡轮弯导叶优化设计流程Fig.6 Optimization design process of bowed guide vane for present axial flow turbine

2.3.1 基于响应面的代理模型

本研究采用遗传算法聚合型(genetic aggregation)响应面方法对样本数据集进行分析处理。该方法是利用遗传算法生成多个响应面模型种群并进行求解，最终实现响应面模型的最优集成。因此它比经典响应面模型准确性更高。该方法的数学描述如下[20]

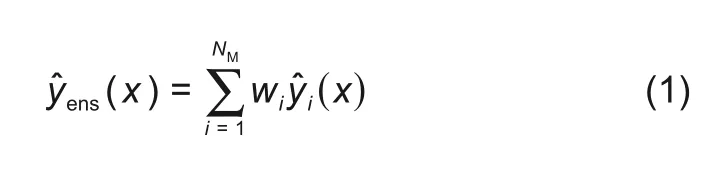
式中，ŷens(x)为集成响应面模型的预测值；ŷi(x)为第i个响应面元模型的预测值；NM为响应面元模型的数量，NM≥1；wi为第i个响应面元模型的权重，该参数满足

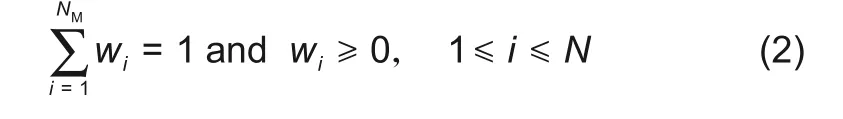
2.3.2 基于遗传算法优化设计

本研究采用的优化模型如计算式(3)所示。该模型以轴流涡轮的等熵效率最大为优化目标，并在优化过程中尽可能保证流量与原型轴流涡轮流量相等。以弯叶片的弯高和弯角为优化自变量，自变量取值范围与表3所示本文研究范围一致。采用混合型非支配排序遗传算法Ⅱ完成最优弯叶片方案的求解，该方法对不同类型数据适应性较好。与此同时选择最大允许帕累托百分比作为收敛准则。

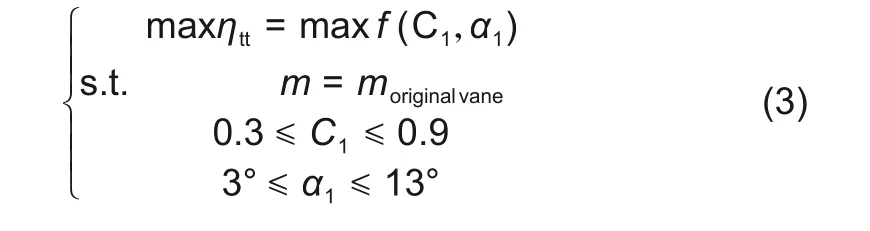
3 结果与讨论

3.1 弯叶片参数对轴流涡轮气动性能影响规律

本文通过CFD模型获得了以轴流涡轮等熵效率、流量为因变量，以导叶弯角和弯高为自变量的样本点集，并基于该点集构建形成了响应面模型，基于该响应面模型，本文首先分析了弯叶片参数对轴流涡轮气动性能的影响规律。如图7(a)所示，轴流涡轮等熵效率-叶片弯角曲线特征会随着弯高的变化而改变：随着弯高的增加，最高等熵效率点对应的叶片弯角值呈减小趋势。在不同的弯高参数下，均存在一个最佳弯角值使轴流涡轮等熵效率最高。在各变化曲线中，轴流涡轮等熵效率的最大值均在90.1%附近。

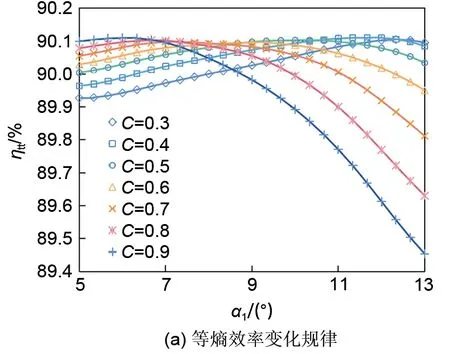
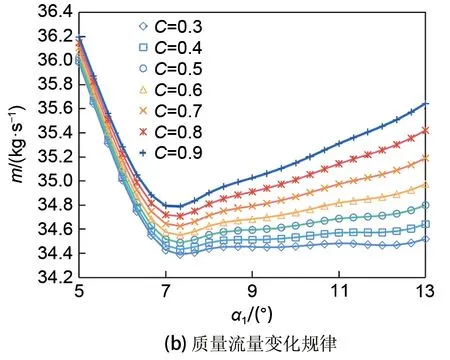
图7 弯叶片参数对轴流涡轮气动性能影响规律Fig.7 Influence of bowed vane parameters on aerodynamic performance of axial flow turbine

图7(b)所示为轴流涡轮质量流量随弯叶片参数的变化规律。如图所示，在不同的弯高值下，轴流涡轮的质量流量均随着弯角先减小，后增大，在弯角值为7°附近时，轴流涡轮质量流量均最小；随着弯高值增加，轴流涡轮最小质量流量值逐渐增加。

3.2 弯叶片参数优化设计

原型导叶与最优弯导叶外形结构和气动性能对比结果分别如图8和表4所示。与原型导叶相比，最优弯导叶的弯曲角和相对弯高分别为12.26°和0.31，弯曲造型主要集中在叶根附近，这也表明最优弯导叶主要对轮毂壁面附近流场进行了调整。见表4，采用最优弯导叶后，轴流涡轮的等熵效率提高了0.77%，而质量流量仅增加0.1 kg/s，占原流量0.29%。这些结果表明，最优弯导叶能够在对轴流涡轮影响很小的条件下在一定程度上提高其等熵效率。

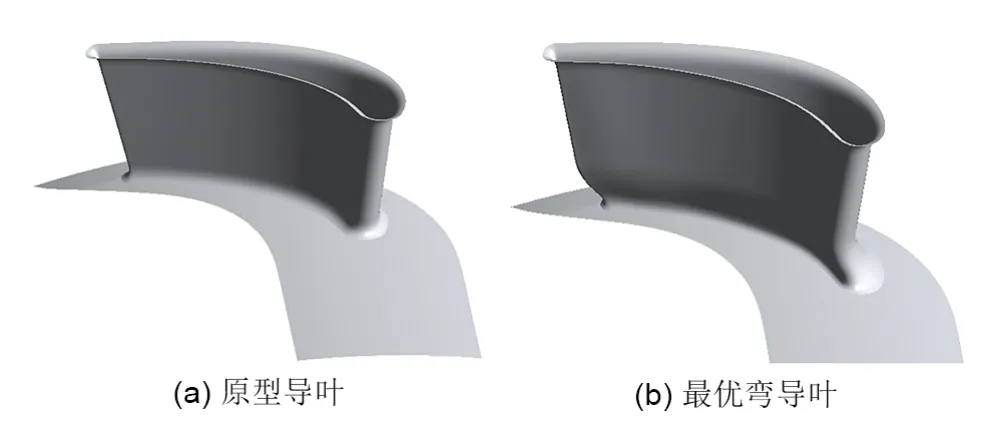
图8 原型导叶与最优弯导叶几何外形对比Fig.8 Geometry comparison between original vane and optimal bowed vane

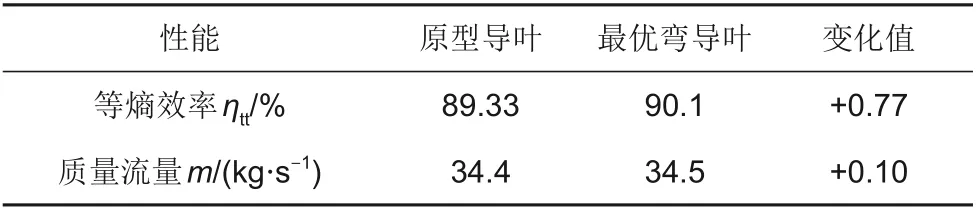
表4 原型导叶与最优弯导叶气动性能对比Table 4 Comparison of aerodynamic performance betweenoriginal statorand optimal bowed stator

3.3 最优弯导叶对轴流涡轮流动损失影响机理

3.3.1 导叶内部流动损失特性

本文首先分析了导叶内部流动场结构及损失特征。图9为原型叶片和最优弯曲造型叶片的导叶出口能量损失系数沿叶高分布。如图所示，最优弯导叶造型对80%叶高以上的能量损失影响较小，并对0.1～0.2相对叶高范围内的能量损失存在部分抑制作用。但是在10%叶高以下，最优弯导叶造型的采用反而使流动损失有略微增加。

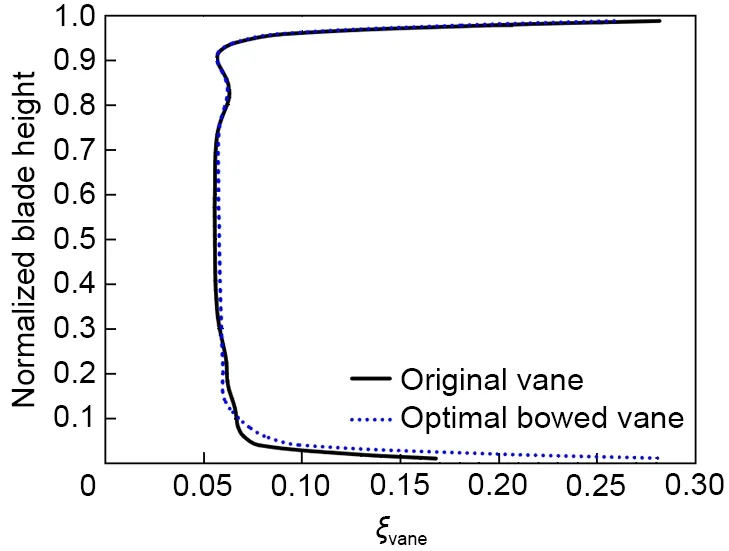
图9 导叶出口能量损失系数沿叶高分布Fig.9 Spanwise distribution of energy loss coefficient at outlet of vane

图10进一步给出了导叶出口熵产分布，以分析最优导叶弯曲造型对其内部流场结构的影响。与原型导叶片相比，代表导叶上通道涡及端壁二次流分布的高熵区域分布特征并未受到明显影响。但是在导叶根部区域，下通道涡分布随着最优弯曲导叶的采用而产生畸变，并且在靠近端壁区域的流动损失显著增加。

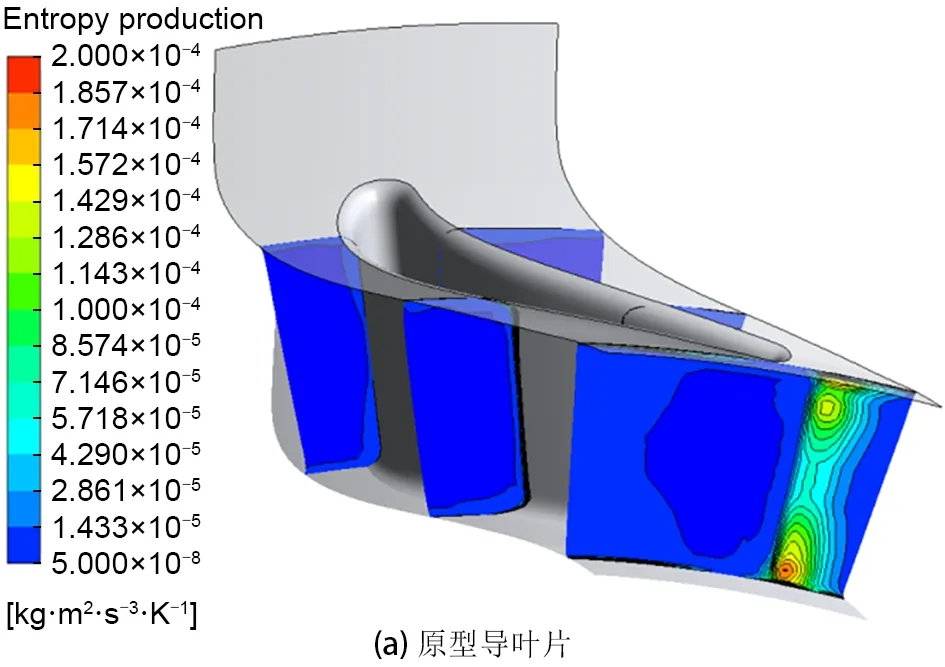
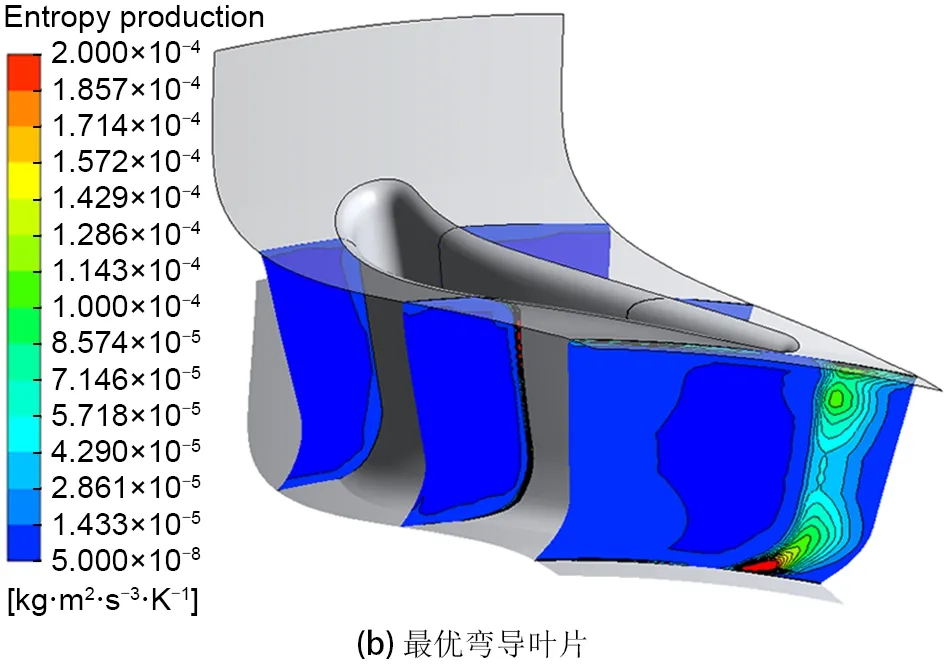
图10 导叶出口熵产分布云图Fig.10 Entropy production distribution at outlet of vane

图11为不同叶高处导叶载荷分布。如图所示，在0.05相对叶高处、0.05～0.6相对流向位置，最优弯导叶吸力面和压力面之间压差明显增加，这会提高相邻叶片之间的压差，强化端壁二次流结构，使端壁附近流动以及下通道涡的流动损失增加；在0.5相对叶高处，除叶片前缘和尾缘两个区域外，两种叶片的载荷差异不大。与此同时，最优弯导叶使叶片前缘区域0.04～0.1相对流向位置的逆压梯度消失，有利于控制流动分离。在尾缘区域，最优弯导叶使0.9～1相对流向位置的叶片载荷降低，有利于控制叶片尾缘脱落涡强度；在0.95相对叶高处，最优弯导叶同样使0.04～0.1相对流向位置的逆压梯度消失，抑制流动分离损失。在0.7相对流向位置处最优弯导叶逆压梯度增加，但叶片尾缘区域载荷减小。

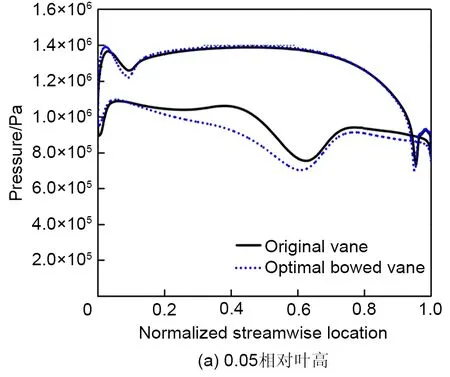
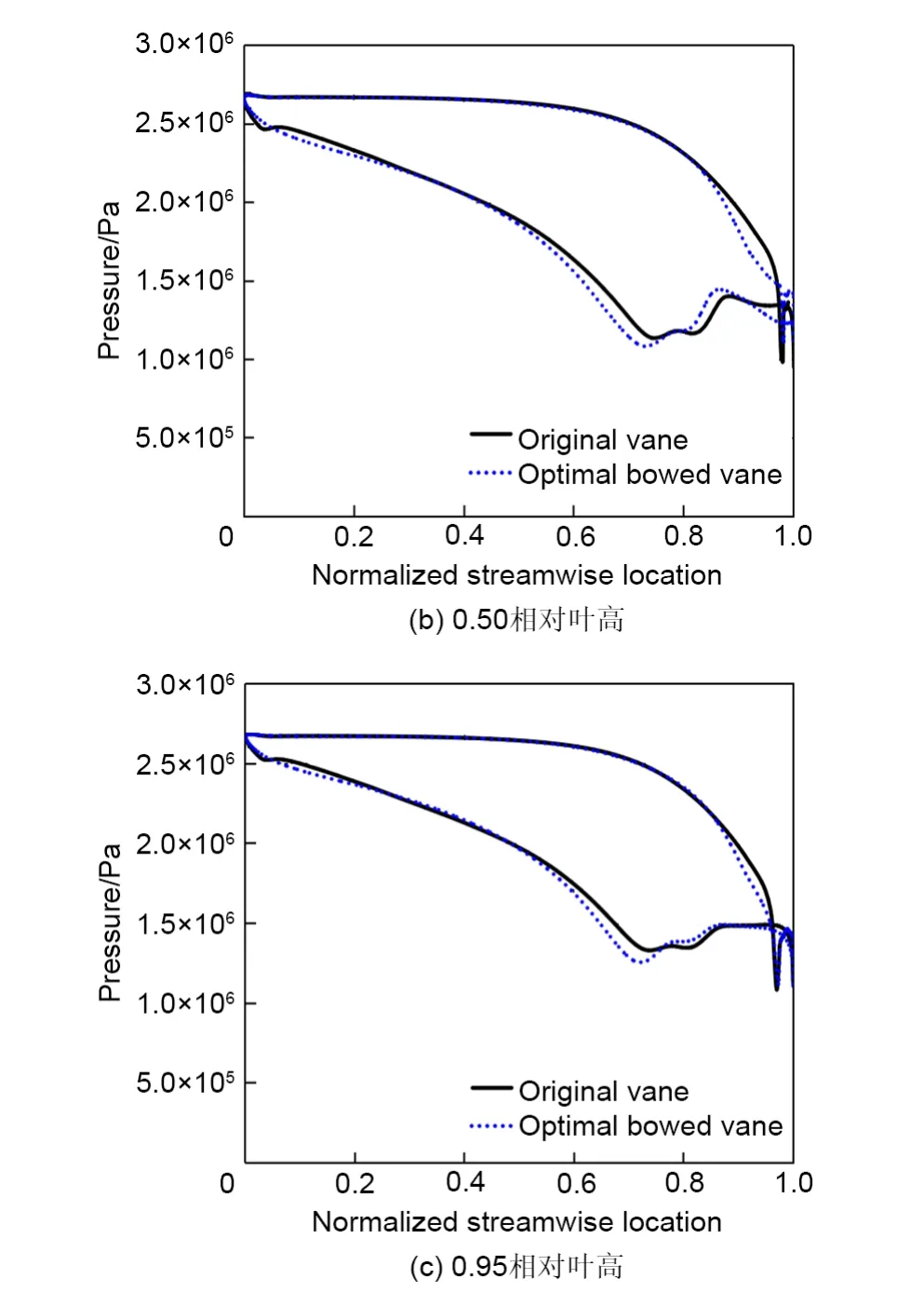
图11 不同叶高处导叶载荷分布Fig.11 Load distribution on vane at different height

综上所述，本文CAES轴流涡轮导叶采用弯曲造型后，对于导叶流道内的流动损失抑制效果并不明显，并且在叶根附近，10%叶高以下区域，由于弯导叶的采用使相邻叶片间横向压差增大，促进端壁二次流发展，反而使流动损失增加。

3.3.2 动叶内部流动损失特性

进一步分析了最优弯导叶对动叶内部流动场结构及损失特征的影响。图12为导叶采用最优弯曲造型前后，动叶出口能量损失系数沿叶高分布。如图所示，采用最优弯曲导叶后，虽然在0～0.10相对叶高区域以及0.50～0.65相对叶高区域内的能量损失系数有所增加，但在0.65～0.95相对叶高区域以及0.15～0.40相对叶高区域内的能量损失系数损失减幅显著，能量损失系数整体上呈现减小特征。产生上述现象的原因在于虽然最优弯导叶使壁面附近流动损失有所增加，但降低了叶顶间隙泄漏涡、上通道涡以及下通道涡引起的流动损失，并改变了上、下通道涡的分布范围。综合分析后表明，最优弯导叶能够有效降低动叶内部的流动损失。

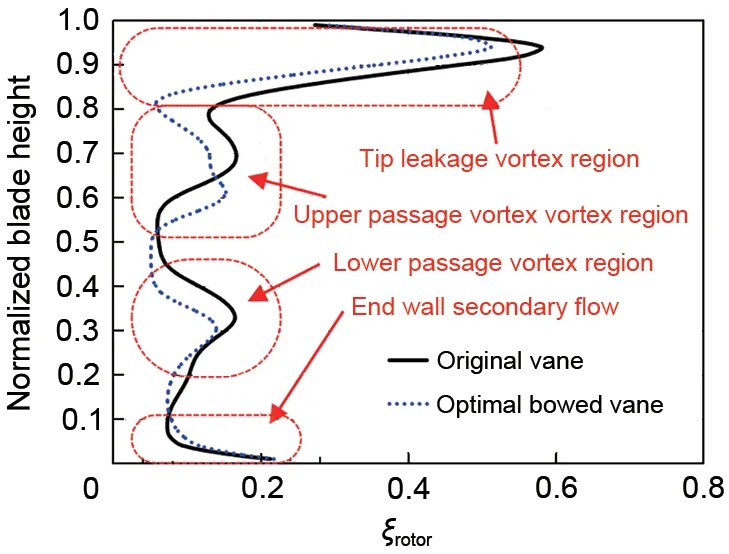
图12 动叶出口能量损失系数ξrotor沿叶高分布Fig.12 Spanwise distribution of energy loss coefficientξrotorat outlet of rotor

图13进一步给出了最优弯导叶对动叶内部流场损失的影响特征。如图所示，采用最优弯导叶后，上通道涡、下通道涡、叶顶间隙泄漏流引发的流动损失整体降低，且上下通道涡引发的高损失区域面积降低。在流场结构方面，动叶下通道涡仅在叶片吸力面附近分布，在流道内的影响范围缩小；叶顶间隙泄漏涡产生位置向叶片下游移动，上通道涡与叶顶间隙泄漏涡耦合作用区发生位置同时向下游移动。

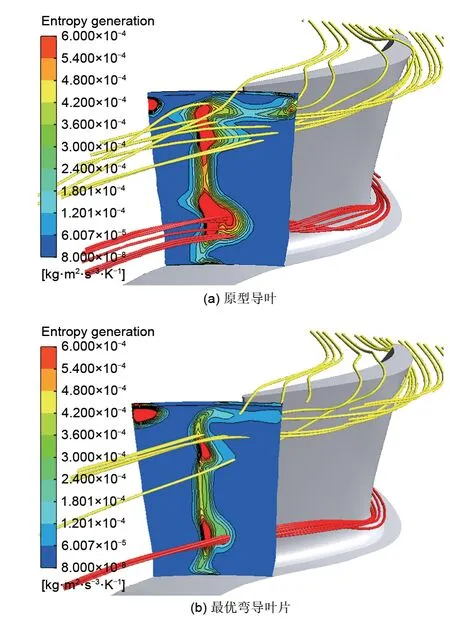
图13 动叶出口熵产分布云图Fig.13 Entropy production distribution at outlet of rotor

图14为最优弯导叶对下游动叶轮毂附近流场影响特征。通过对比后发现，最优弯导叶几乎消除了动叶前缘根部的滞止鞍点(图中红色虚线圈)，马蹄涡的影响范围减小并且仅集中在叶片吸力面附近。与此同时，最优弯导叶也会对叶顶间隙区域流场产生影响。如图15所示，最优弯导叶也使叶顶前缘的鞍点位置向下游后移，并使叶顶马蹄涡吸力面分支影响范围减小，延迟了叶顶间隙泄漏流的产生位置。

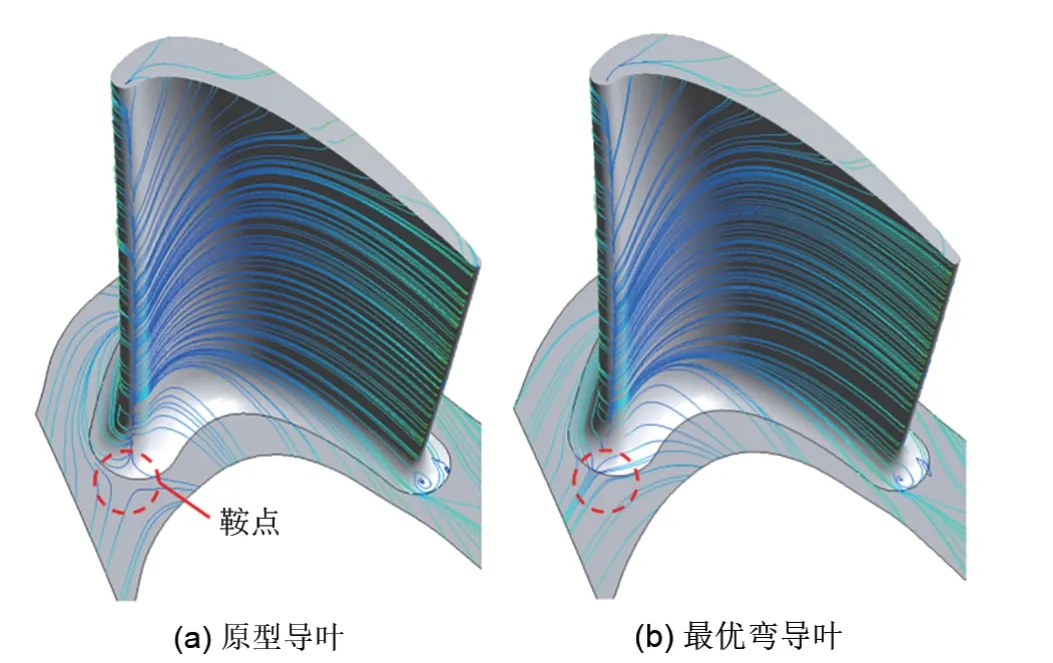
图14 最优弯导叶对下游动叶轮毂附近流场影响特征Fig.14 Influence of optimal bowed vane on flow field near hub of rotor

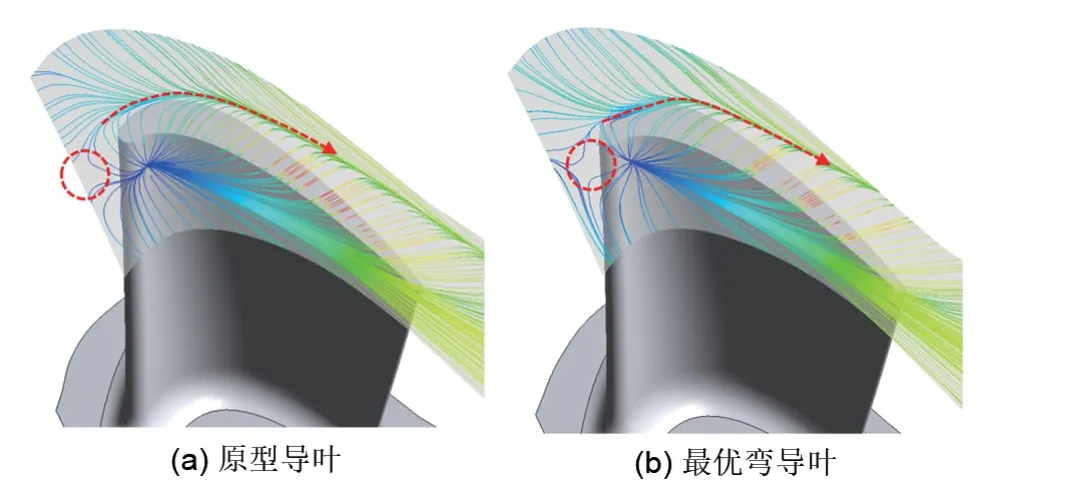
图15 最优弯导叶对下游动叶叶顶间隙区域流场影响特征Fig.15 Influence of optimal bowed vane on flow field in blade tip clearance region of rotor

上述动叶进口气流角的改变也会对动叶片载荷产生影响。图16为不同叶高处动叶载荷分布。采用最优弯导叶后，0.05相对叶高处的叶片载荷增加，这会提高相邻导叶片之间的横向压差，强化端壁二次流结构，造成该区域流动损失增加(图12)。但另一方面，这种压差也迫使马蹄涡吸力面分支仅集中在叶片表面附近，抑制了通道涡的影响范围以及由此产生的流动损失；在0.5相对叶高处，除叶片前缘和尾缘两个区域外，两种叶片的载荷差异不大；在0.95相对叶高处、0.1～0.3相对流向区域内，动叶叶片载荷降低，减小了叶顶间隙泄漏流的驱动力，抑制叶顶间隙泄漏流的形成和发展，减小了叶顶间隙泄漏流损失。

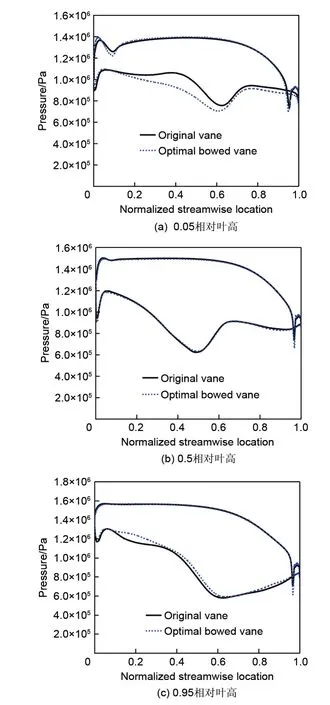
图16 不同叶高处动叶片载荷分布Fig.16 Load distribution on rotor blade at different height

3.3.3 最优弯导叶对CAES轴流涡轮流动损失影响机理

上述分析表明，采用最优弯曲造型后导叶叶片载荷发生变化，并对端壁横向二次流产生影响，因此会对涡量分布产生影响。图17为最优弯几何对导叶内部涡量分布影响特征。其中涡量采用用螺旋度(helicity)H来表征，其定义如下

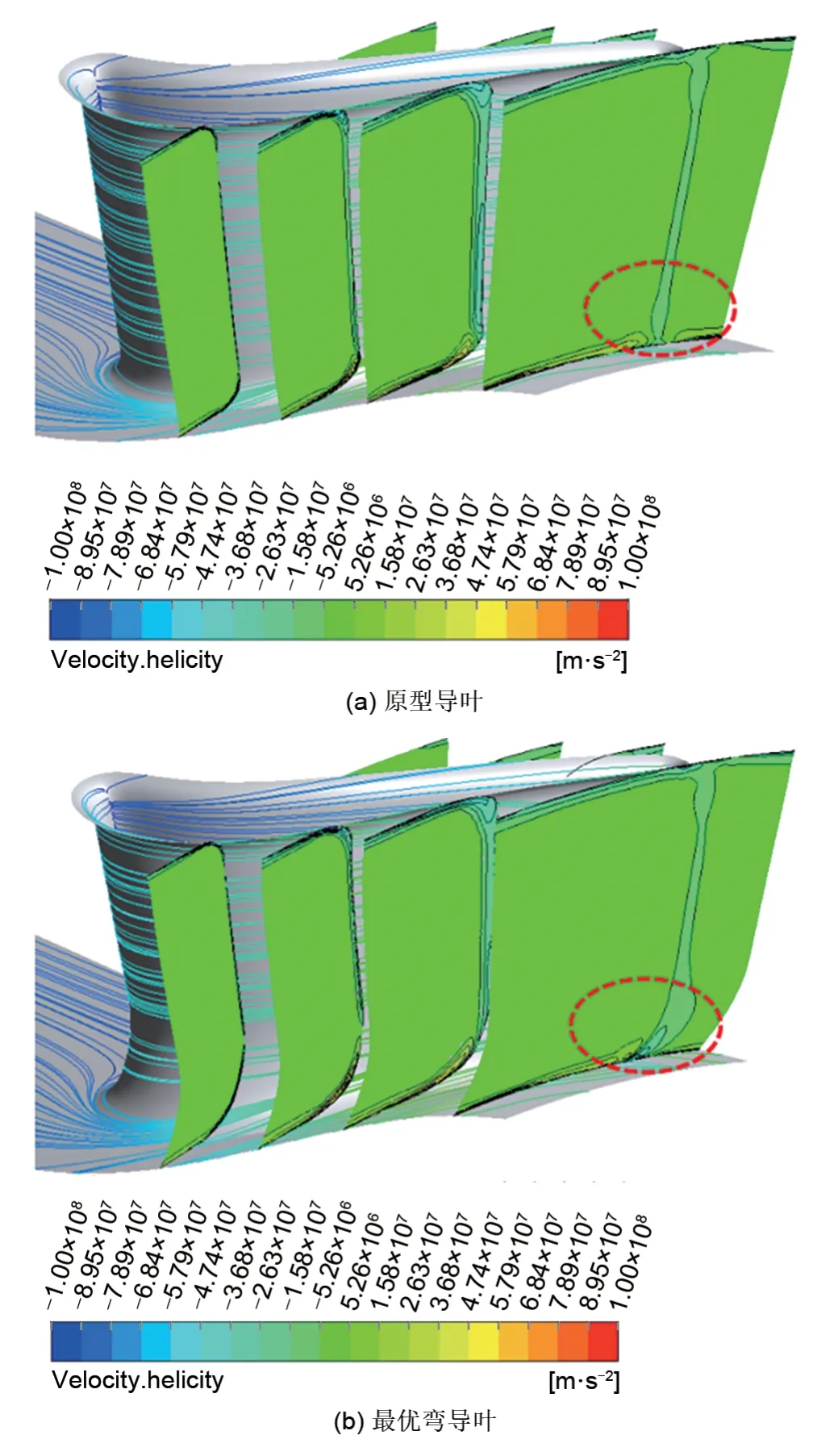
图17 最优弯几何对导叶内部涡量分布影响特征Fig.17 Influence of optimal bowed geomtry on internal vorticity distribution

式中，H为螺旋度；ω为涡量；U为速度矢量。

如图17所示，采用最优弯曲造型之后，导叶叶根附近旋涡螺旋度有显著变化，这种变化使导叶尾缘端壁附近气流方向发生显著改变，并进一步使动叶进口气流角发生变化。为揭示这种气流角变化特征，图18展示了动叶进口相对气流角沿叶高分布。由该图可知，最优弯导叶对下端壁气流角的影响较大，特别是在轮毂壁面附近。当采用最优弯导叶时，0.15相对叶高以下的气流角显著减小；与此同时，由于导叶弯曲造型也会对流道径向压力分布产生影响，并因此对上端壁附近二次流也有作用，使0.94叶高以上的气流角有略微减小。

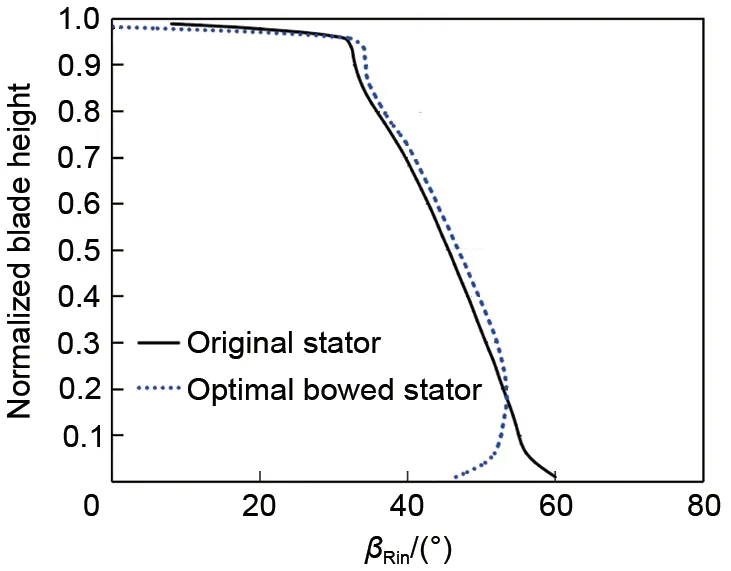
图18 动叶进口相对气流角沿叶高分布Fig.18 Spanwise distribution of relative flow angle at inlet of rotor

综合上述分析，最终获得最优弯导叶对流动损失影响机理如下：①导叶采用最优弯曲造型后，改变了流场压力分布及叶片表面载荷分布，强化了下端壁二次流，增大了通道涡强度，改变了导叶出口气流角，并通过径向压力分布对上端壁出口气流角产生部分作用；②随着导叶出口气流角变化，动叶轮毂和机匣附近的进口气流角也随之降低，减小了叶栅攻角，改变了流道内压力场分布，基本消除了动叶前缘根部的滞止鞍点，同时增加叶根区域叶片载荷，虽然在一定程度上强化了轮毂端壁横向二次流，但是也抑制了叶根马蹄涡的影响范围强度，最终使下通道涡引起的流动损失降低；③动叶进口气流角的减小，也促使叶顶前缘鞍点位置向下游后移，并使叶顶马蹄涡吸力面分支影响范围减小，延迟了叶顶间隙泄漏流的产生位置，降低了泄漏流与上通道涡的掺混，减小了叶顶间隙泄漏涡和上通道涡损失。此外，最优弯导叶并未对其自身内部流场损失有明显改善。这一现象也再次说明，弯曲造型对导叶和动叶流场存在复杂影响，需要全面考虑导叶与动叶的相互作用，以获得整级性能的全面提升。

最优弯导叶对CAES轴流涡轮流动损失的作用机理也与其他领域的涡轮不同。表5归纳了弯导叶在不同领域涡轮上的结构形式和损失控制机理的差异。如该表所示，弯导叶对空气储能涡轮和其他应用领域涡轮损失的影响机理存在两点不同。一是主要作用部件不同。对于其他领域涡轮，弯导叶对导叶和动叶内部的流动损失均有不同程度的改善，而对于本文空气储能涡轮，弯导叶主要是对动叶内部流动损失产生抑制。二是作用的流场结构不同。对于其他领域涡轮，弯导叶也会对激波损失、逆压梯度引起的分离损失产生影响；而对于空气储能涡轮，弯导叶主要影响动叶内部叶顶间隙泄漏涡、上下通道涡等通道内二次流损失。此外，最优弯曲造型随着涡轮结构和应用领域而变化。

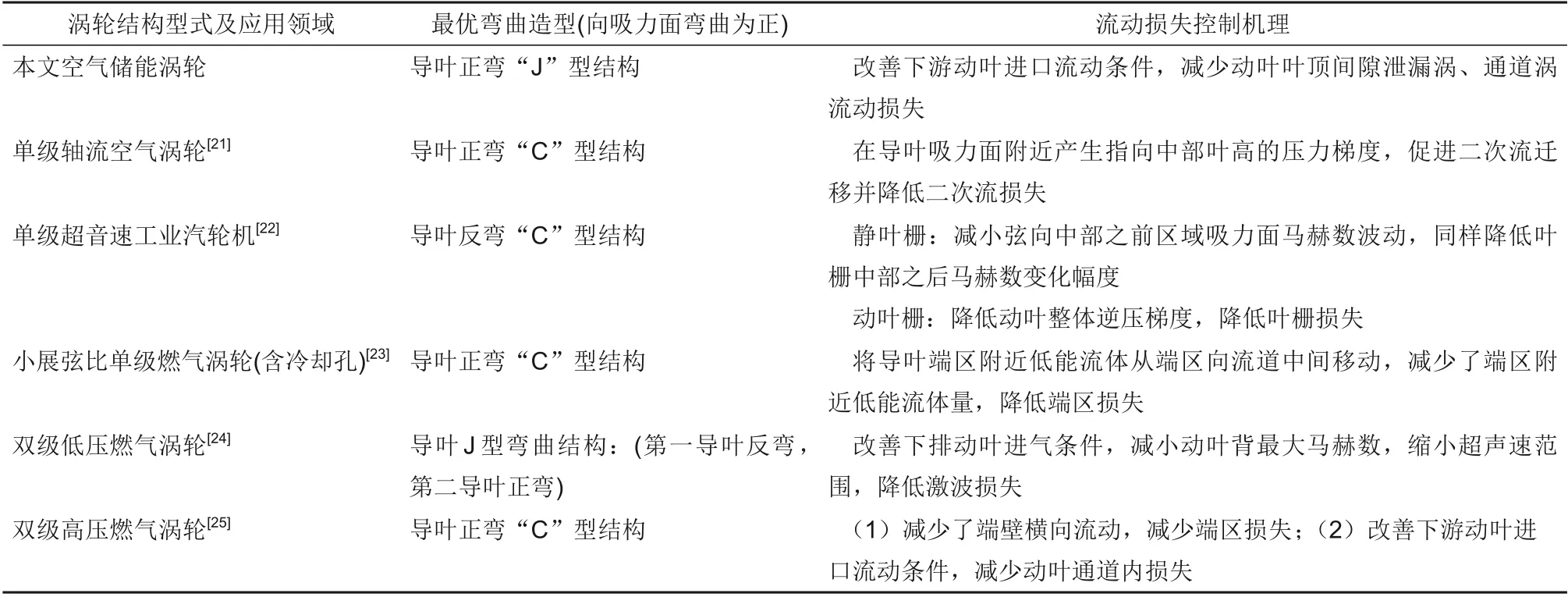
表5 空气储能涡轮弯导叶与其他轴流涡轮弯导叶在最优结构形式和流动损失控制机理对比Table 5 Comparison of optimal structure and flow loss control mechanism of bowed vanes of axial turbines in CAES and other fields

4 结 论

本文以弯高和弯曲角为自变量，以等熵效率为优化目标，通过CFD模型获得样本点数据集，并以此构建响应面模型，采用遗传算法完成了压缩空气轴流涡轮弯导叶优化设计，使轴流涡轮在对流量影响较小的条件下实现了等熵效率进一步提升，并进一步分析了最优弯导叶对流动损失的影响机理，获得的结论如下。

（1）通过对CFD模型的求解样本点数据集，构建了响应面模型并获得了导叶弯高和弯曲角对轴流涡轮等熵效率和流量的影响规律：随弯高增加，轴流涡轮最高等熵效率点对应叶片弯角值呈减小趋势。在不同的弯高参数下，均存在一个最佳弯角值。整体上轴流涡轮等熵效率的最大值均在90.1%附近。与此同时，轴流涡轮质量流量均随着弯角先减小后增大，并在弯角值为7°附近时其值最小。

（2）优化设计结果表明，最优弯曲角和相对弯高分别为12.26°和0.31。弯导叶在叶根附近有明显的弯曲造型特征。采用最优弯导叶后，轴流涡轮的等熵效率提高了0.77%，而质量流量仅增加0.29%。这一结果表明，最优弯导叶能够在对轴流涡轮影响很小的条件下在一定程度上提高其等熵效率。

（3）最优弯导叶对CAES轴流涡轮流场的作用效果与其他领域涡轮存在不同：最优弯导叶主要对动叶内部通道损失产生抑制作用。具体而言，最优弯导叶使轮毂和机匣附近的动叶进口气流角减少。这一改变一方面消除了动叶前缘根部的滞止鞍点，减少了马蹄涡影响范围以及与端壁二次流的作用路径和强度，抑制了下通道涡引起流动损失；另一方面，也使叶顶前缘的鞍点位置向下游后移，吸力面马蹄涡分支影响范围减小，集中在叶片吸力面附近，由此使上通道涡与周边流体作用降低，流动损失减小。