跨声速轴流压缩机动静叶弯参数耦合关系

张 丹 ，左志涛 ,,4，周鑫 ，郭文宾 ，陈海生 ，王星

（1中国科学院工程热物理研究所，北京 100190；2中国科学院大学，北京 100049；3毕节高新技术产业开发区国家能源大规模物理储能技术研发中心，贵州 毕节 551712；4中科南京未来能源系统研究院，江苏 南京 211135）

执行“碳达峰、碳中和”任务，需要减少石油、天然气、煤等不可再生能源的发电比例，大力发展水电、风电、光伏发电等可再生清洁能源。与传统能源相比，可再生能源电力输出具有不稳定性、不平滑性、波动性、间歇性和随机性等特性，这些特性对电网安全存在很大的威胁[1]。压缩空气储能(CAES)系统既可用于削峰填谷，也可使不稳定电力平滑输出，增强电网的抗冲击能力，提高调节幅度，更好地实现供需平衡，从而提高供电安全性和经济性[2-4]。压缩机是CAES系统的关键部件之一，其作用是利用待存储的电能对空气做功使其压缩，将电能转化为压力势能和内能存储起来[5]。CAES系统采用的压缩机需要有流量大、工况宽、效率高等特点，而轴流压缩机虽然具有流量大、效率高等优点，但是其稳定工作范围较窄[6]。因此，要将轴流压缩机广泛应用于CAES系统，就需要针对提高其稳定工作范围进行深入研究。

就这一研究课题，诸多学者开展相关研究工作，包括主动流动控制措施，如附面层抽吸[7]、叶尖喷气[8]等，以及被动控制方法，如机匣处理[9]、涡流发生器[10]、非轴对称端壁成型[11]、弯掠技术[12-14]等。由于主动流动控制会增加系统的复杂性和维护成本，在压缩空气储能系统中更倾向于采用被动控制方法。弯掠技术是提高轴流压缩机气动性能的有效措施之一。

1963年，Smith等[12]针对NACA翼型进行弯掠叶片的实验研究，提出在轴流叶轮机械设计中考虑弯和掠影响的近似方法。1984年，Breugelmans等[13]针对NACA叶片进行实验研究，发现弯叶片对二次流的发展有着较大的影响。1990年，王仲奇等[14]研究弯叶片对气流参数沿叶高方向分布的影响，发现弯叶片能够增大最小气流角，减小最大气流角，在叶展方向，使气流角更加接近设计值，从而改善叶片的气动性能。1997年，Weingold等[15]对三级轴流压缩机进行研究，发现弯叶片会使流场产生径向力，降低吸力面角区的扩散速度，延迟角区分离。1999年，Denton等[16]指出弯叶片可以减少端壁损失、叶尖泄漏损失，并总结出3种机理，这3种机理从不同的角度解释为什么采用弯叶片会减少端壁损失。2001年，Wenger等[17]采用三维Navier-Stokes数值计算方法，比较直静叶与弯掠静叶的流场和性能参数，发现弯掠叶片可以改善载荷的径向分布和端壁边界层的发展。随后，Galimore等[18]对亚音速压缩机进行研究，发现径向叶片力有利于减少压缩机损失。但是，并不是所有的弯掠都能提高效率、增加失速裕度，Denton等[19]发现虽然弯掠使通道激波远离叶片前缘，提高失速裕度，但是对风机的最高效率影响不大。2007年，Benini等[20]以NASA Stage37为原型，采用CFX进行数值模拟，发现前弯可以削弱激波，使总体效率得到大幅度的提高，前弯与后弯对阻塞流量的影响都不明显。2008年，毛明明等[21]发现弯掠动叶可以降低端壁损失，增加静叶进口边界条件的径向均匀性，从而使压气机级效率显著提高。2017年，Taylor等[22]详细介绍如何通过改变叶片的三维堆叠来改变径向压力梯度，从而改变压缩机的气动性能。吕从鹏等[23]研究发现，前弯、后弯、弯掠对处于设计转速和部分转速工况下的压气机的性能影响是不同的，设计转速时前掠与反弯的组合弯掠优于前掠与正弯的组合弯掠，而部分转速时正好相反。2020年，杨梦柯等[24]对某高负荷压气机进行数值模拟，分别研究弯叶片对压缩机叶展中部、端壁区域、叶片尾缘流动情况的影响。

综合之前的研究结果，弯能够在很大程度上提高轴流压缩机的气动性能，但是之前研究基本只针对单排静叶或者动叶，没有将动叶与静叶结合起来研究弯对轴流压缩机性能的影响。考虑到动叶的积叠参数发生变化后，马赫数、气流出口角、尾迹等气动参数等也会随之发生变化，影响下游的静叶流场，本文选取NASA Stage35为原型叶片，通过数值方法研究动叶与静叶的弯参数耦合关系。

正交试验设计是一种多因数多水平优化问题的科学方法，具有正交性、可比性，能够大幅减少试验次数[25]。考虑到本研究参数多及正交试验设计的优点，本文采用正交试验法，以增加失速裕度、峰值效率和最大压比作为优化目标，以动叶弯角/高、静叶弯角/高作为试验因素进行方案设计，研究动静叶弯参数的耦合关系。

1 研究对象及数值计算方法

1.1 研究对象

为研究动叶及静叶的弯参数耦合关系，以NASA Stage35为原型，在其他参数不变的前提下，通过修改动静叶弯参数设计一系列不同弯角和弯高的弯叶片结构。

NASA Stage35是美国国家航天航空局Lewis研究中心研发的跨声速级低展弦比进口级之一[26-27]。其设计参数见表1。

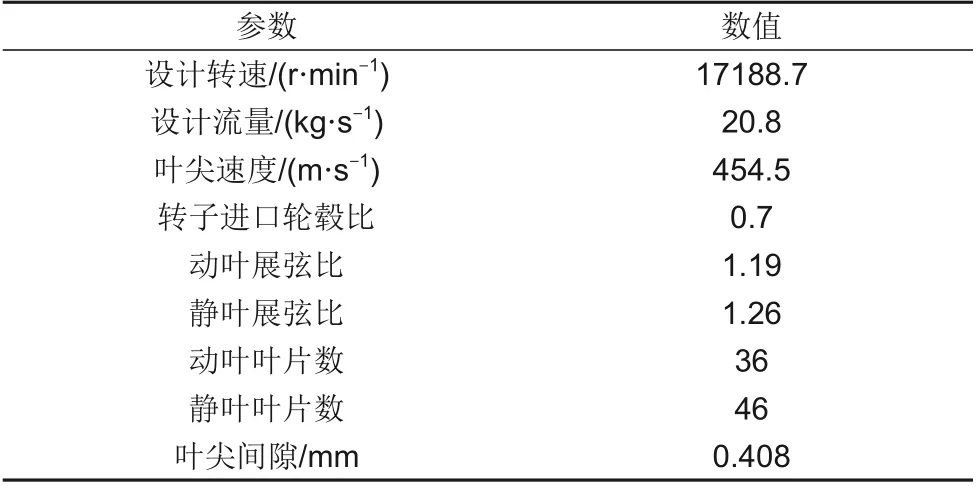
表1 NASA Stage35设计参数Table 1 NASA Stage35 design parameters

本研究中采用1998年Sasaki等[28]对弯叶片的定义，即当叶片积叠线弯曲方向垂直于叶片弦线方向时，称为弯叶片，如图1所示。当压力面与轮毂成锐角时，称为前弯；当压力面与轮毂成钝角时，称为后弯。定义弯叶片的积叠曲线由1条直线和1条具有3个控制点的二阶Bezier曲线组成。其中c为叶片弯高，α为叶片弯角，f为分数因子。f定义为贝塞尔曲线的第2个控制点位置，且对于所有弯叶片都为0.5c。

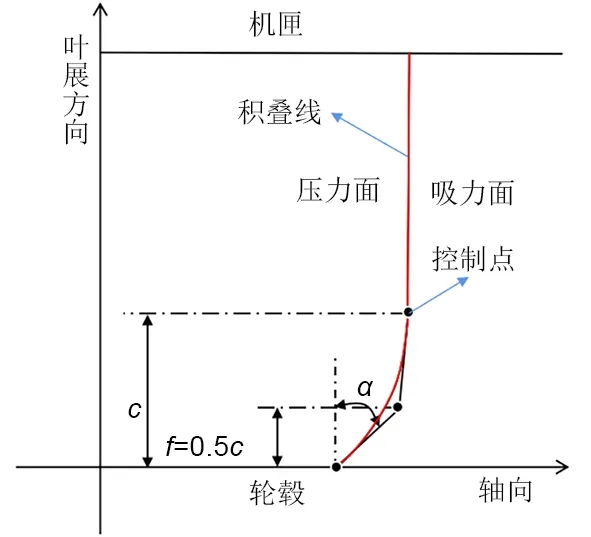
图1 弯叶片的定义Fig.1 Definition of compound lean blades

1.2 数值计算方法及验证

本文的数值计算采用NUMECA软件，基于三维稳态、可压缩条件来求解Navier-Stocks方程。方程的空间离散采用二阶精度中心差分格式，时间离散采用四阶Runge-Kutta方程，湍流模型选取Spalart-Allmaras。动静交界面采用周向守恒型连接面，计算过程中采用多重网格法以及当地时间步长加速收敛技术来缩短计算周期。

边界条件：入口边界条件设置总压(101325 Pa)、总温(288.2 K)、湍流黏度(5×10−5m2/s)；固体壁面条件设置为绝热无滑移，转子叶片和轮毂设定为恒定转速(17188.7 r/min)，机匣和静叶保持静止；出口边界条件采用径向平均静压。收敛标准为RMS和最大残差均小于1×10−6。因为在堵塞点附近气动性能对流量变化比较敏感，而近失速点附近对背压变化比较敏感，因此根据特性曲线趋势，以排气压力110000 Pa为起始点，以5000 Pa为间隔逐渐增加背压直到计算无法收敛，然后出口改用流量边界条件，即以上一工况点的出口流量作为出口边界条件，以0.2 kg/s为间隔逐渐减少质量流量直到计算无法收敛。

计算区域为单通道，采用AutoGrid5进行网格划分，自动生成O4H型网格结构，叶尖间隙沿径向有17个网格点。为保证近壁面的计算精度，网格无量纲高度y+应接近1，设置近壁面第1层网格点与壁面的距离为3×10−6m。为使数值计算精度满足要求的同时减少计算量，采用上述拓扑结构分别划分50万～450万的网格结构，并在设计工况下进行数值模拟，得到不同网格数下的总压比和等熵效率性能曲线，如图2所示。从图中可以看出，随着网格数量增加，总压比、等熵效率、稳定工作范围均增加，当网格数量超过300万时，数值模拟结果基本保持不变，考虑到精度要求与计算量限制，选择300万作为网格数目。

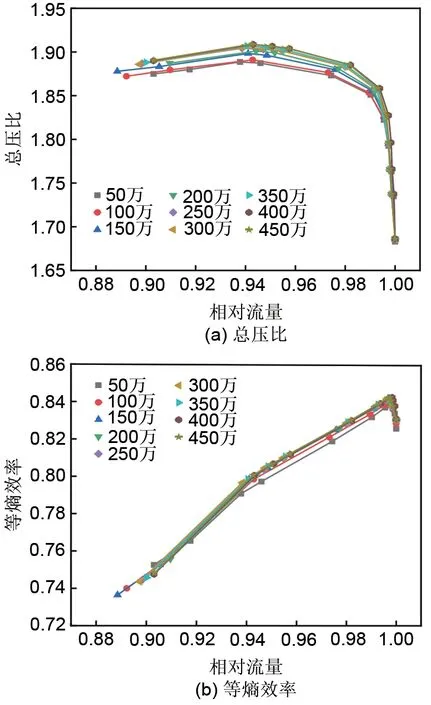
图2 不同网格下NASA Stage35的性能曲线Fig.2 Performance curves of NASA Stage35 with different grid numbers

为验证数值计算方法可靠，将100%转速以及90%转速下数值模拟得到的数据与实验数据进行对比，实验数据来自Lewis实验中心单级跨声速轴流压缩机实验台[26]。图3为NASA Stage35不同转速下数值结果与实验结果的对比图，从图中可以看出，大流量下总压比的数值结果略高于实验结果，随着流量减小，数值模拟得到的结果略低于实验结果；对于等熵效率，100%转速与90%转速下，大部分数值结果低于实验结果。压比的最大相对误差为2.03%，效率的最大相对误差为2.47%，误差可能主要来源于两点：①在数值模拟过程中假设壁面条件为绝热无滑移，而在实验过程中壁面并非是绝热的；②实验过程存在测量等误差。数值模拟得到的压比、效率特性曲线的走势与实验相似，本文选用的模拟软件与数值计算方法可以较好地预测轴流压缩机的性能。

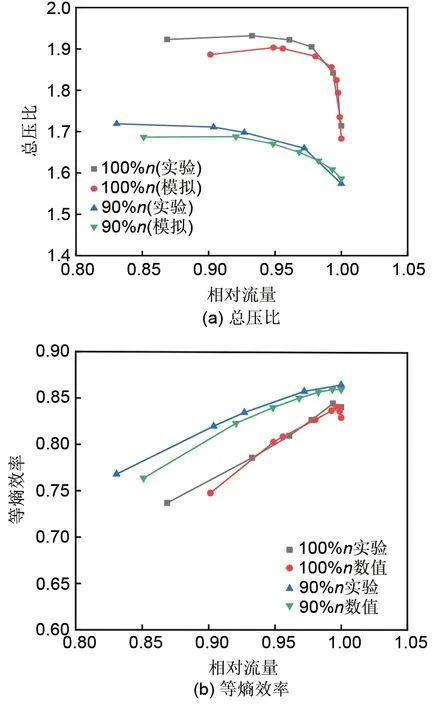
图3 NASA Stage35数值结果与实验结果对比Fig.3 NASA Stage35 numerical results compared to experimental results

2 正交试验设计

本文主要研究动静叶弯参数的耦合关系，而定义弯叶片的主要参数有弯角、弯高，因此选取动叶弯角(α1)、动叶弯高(c1)、静叶弯角(α2)、静叶弯高(c2)作为试验因素，每个因素根据文献和经验，分别选取7个水平，见表2。根据试验因素与试验水平选取L49(74)正交表，正交试验方案见表3，其中直叶片的因素组合为模型25。以NASA Stage35为原型，根据正交试验表采用AutoBlade进行参数化建模。

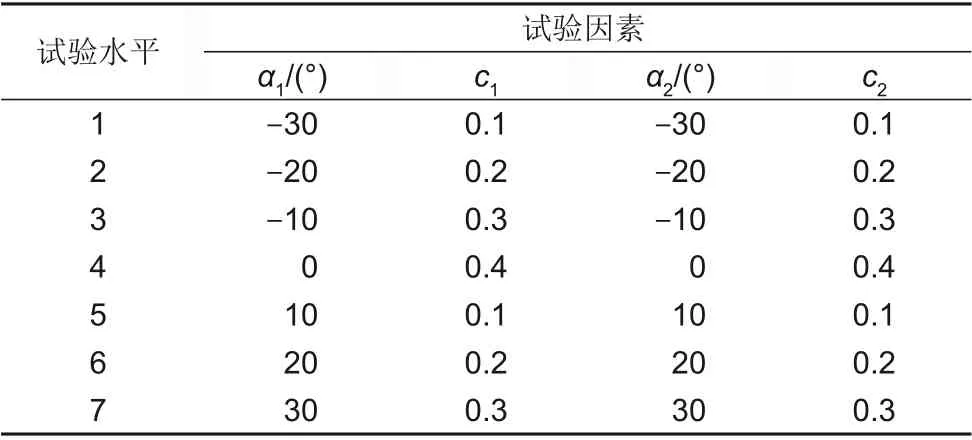
表2 正交因素水平表Table 2 Orthogonal factor level table

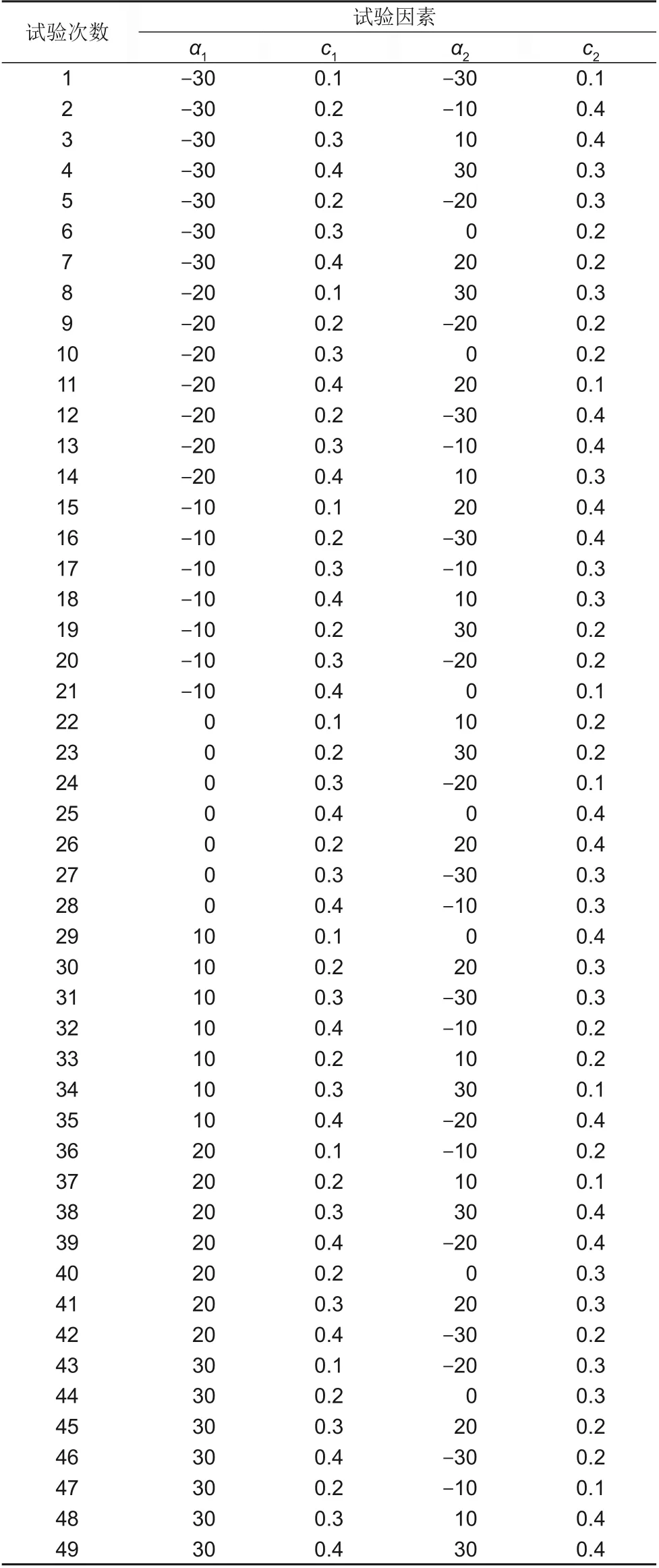
表3 正交试验方案Table 3 Orthogonal test scheme

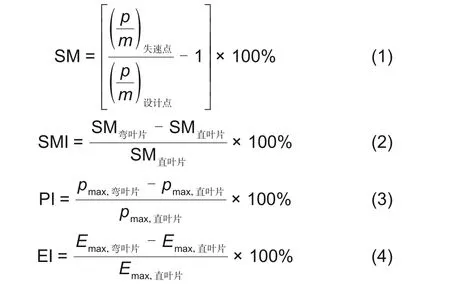
将轴流压缩机运用在CAES系统中，需要较大的失速裕度(SM)，但也需要兼顾压比与效率。因此选取失速裕度增量(SMI)、峰值效率增量(EI)、最大压比增量(PI)作为优化目标。本文将研究4个试验参数对这3个优化目标的影响大小，在尽可能提高SM的前提下，减少峰值效率与最大压比的降低。SM、SMI、EI、PI的计算式如式(1)～(4)所示。采用叶尖泄漏流与主流的交界面到达叶片前缘作为失速起始点的标志[29]。

3 试验结果及分析

3.1 试验结果

根据数值模拟结果，通过计算式(1)～(4)可以计算得到SMI、EI、PI，结果如图4所示。

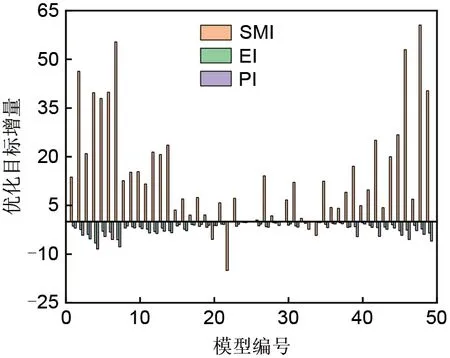
图4 正交试验结果Fig.4 Results of orthogonal test

从图4可以看出，对于失速裕度，除模型20、22、24、29、33、34外，采用弯叶片后，压缩机的失速裕度均有不同程度的增加，其中模型48的失速裕度增加最多，增加60.56%；对于峰值效率，采用弯叶片后，所有的模型的峰值效率均降低，其中模型4的峰值效率下降最多，降低6.54%；对于最大压比，除模型22，其余模型的最大压比均有不同程度减小，其中模型4下降最多，达8.41%。

3.2 极差分析

极差分析是一种比较直观的分析方法，通过比较每个水平试验时平均值的大小，分析不同水平的优劣；通过比较每个因素的极差，分析不同因素对试验目标影响的大小。为分析各个试验参数对试验目标的影响大小，寻找动静叶弯参数的耦合关系，优化NASA Stage35，对数值结果进行极差分析。Mi为试验因素取水平i时，数值模拟结果的平均值；R为各试验目标平均值Mi的极差。

分析表4，比较R可以看出，4个实验因素对失速裕度影响大小的排序为α1>c1>c2>α2，对效率影响大小的排序为α1>α2>c1>c2，对最大压比的影响排序为α1>c1>α2>c2，其中动叶弯角对3个优化目标的影响最大。

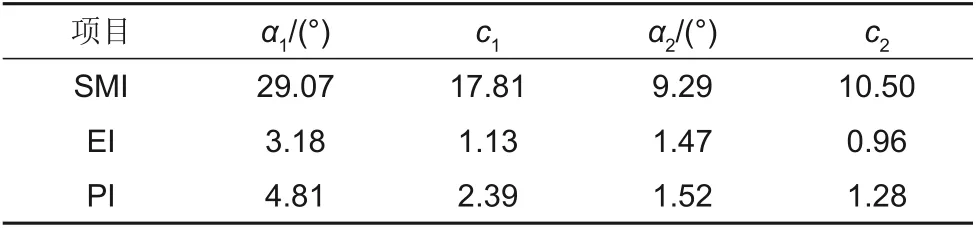
表4 4个实验因素的极差RTable 4 Range of 4 experiment cases

从图5可以看出，随着动叶弯角从−30°增加到30°，失速裕度的平均值Mi先减小后增大；随着动叶弯高从0.1增加到0.4，失速裕度的平均值Mi逐渐增加。Mi均大于0，可以得出对于NASA Stage35，采用合适的弯叶片确实能增加失速裕度。静叶弯高与失速裕度之间没有比较明显的线性规律，可能是静叶对失速裕度的影响相对动叶较小，且改变静叶弯高的同时，改变其他叶片弯参数，从而产生影响。

从图6可以看出，随着动叶弯角从−30°增加到30°时，峰值效率的平均值Mi先增大后减小，在动叶弯角为10°的时候达到最大值。Mi随静叶弯角的变化趋势亦是如此，当静叶弯角为0°时，Mi达到最大值，当弯角为−30°时，Mi下降最多，下降3.71%；当动叶弯高从0.1逐渐增到0.4时，Mi逐渐减少，静叶弯高与之相似。

从图7可以看出，当动叶弯角从−30°增加到30°时，最大压比的平均值Mi先增大后减小，在动叶弯角为0°时达到最大值，同样角度的后弯会比前弯带来的损失更大；Mi随静叶弯角的变化与之相同。Mi随着动叶弯高增加逐渐减小，但是静叶弯高没有明显的规律，可能是静叶弯高对压比的影响相对其他参数较小，且改变静叶弯高的同时，改变其他弯参数，从而产生影响，使其规律不明显。

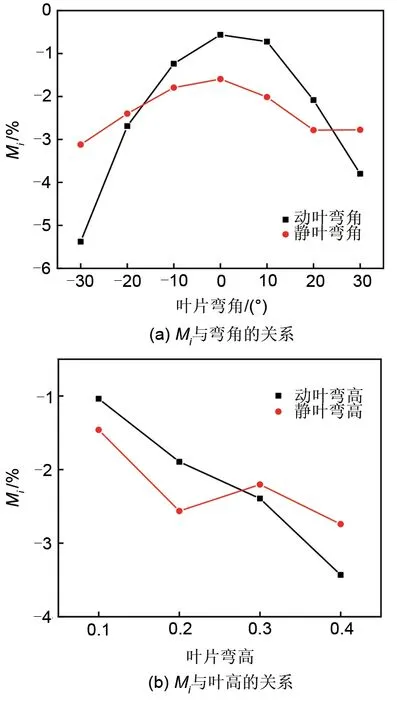
图7 PI的极差分析Fig.7 Range analysis of PI

综上所述，采用弯叶片能够提高失速裕度，但是会减小峰值效率、最大压比。动叶弯角对3个优化目标的影响最大，图8为3个优化目标随动静叶弯角变化的云图。当动叶静叶弯角绝对值小于10°时，失速裕度增幅不明显甚至降低，但是峰值效率、最大压比的下降幅度较小。当−30°的动叶弯角与20°、30°的静叶弯角匹配时，失速裕度有一定的增加，但是峰值效率与最大压比存在大幅下降。当30°的动叶弯角与10°的静叶弯角匹配时，峰值效率与最大压比的下降幅度较小，且失速裕度有很大的提高，与之相对应的模型为48号，考虑到CAES系统3个优化目标，选取48号模型为最优模型。

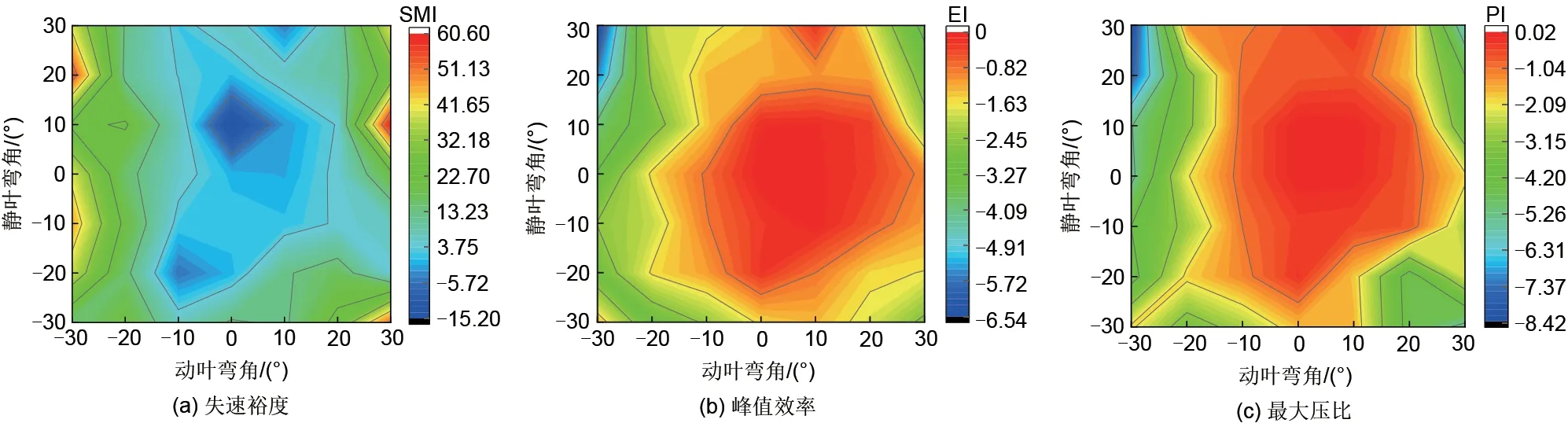
图8 3个优化目标随动静叶弯角变化的云图Fig.8 Nephogram of three optimization objectives changing with compound lean angle of rotor and stator

3.3 弯叶片对叶尖泄漏流的影响

为进一步探究弯叶片对失速裕度、峰值效率、最大压比产生影响的原因，本文以动叶弯角30°、动叶弯高0.3、静叶弯角10°、静叶弯高0.4的最优组合为例，与直叶片内部流动结构进行对比分析。

采用弯叶片可以增加失速裕度，减缓叶尖泄漏涡的发展，延迟叶尖泄漏流与主流的交界面到达相邻叶片前缘，从而推迟失速出现。从图9可以看出，在设计工况时，弯叶片与直叶片叶尖处的最大熵产在动叶尾缘，主要由附面层分离导致。弯叶片叶尖泄漏涡产生的熵产小于直叶片，推测在设计工况时，弯叶片的泄漏涡强度小于直叶片。从图10可以看出弯叶片的叶尖泄漏涡更加狭长，范围更小，这证实上述的推测。从图11可以看出，当到达失速点时，叶尖处的最大熵产由叶尖泄漏涡导致，同时相比于设计工况，尾缘附面层分离向上游移动。静叶吸力面出现的高熵区，主要由附面层分离导致。从图11、图12可以看出，当到达失速点时，两个模型的熵分布与泄漏涡结构均类似，这与本研究采用的失速判定相符合。采用弯叶片可以改善叶尖附近的流动情况，减慢叶顶间隙泄漏涡的扩散速率，延迟动叶叶尖泄漏流与主流的交界面到达叶尖前缘，从而提高失速裕度。

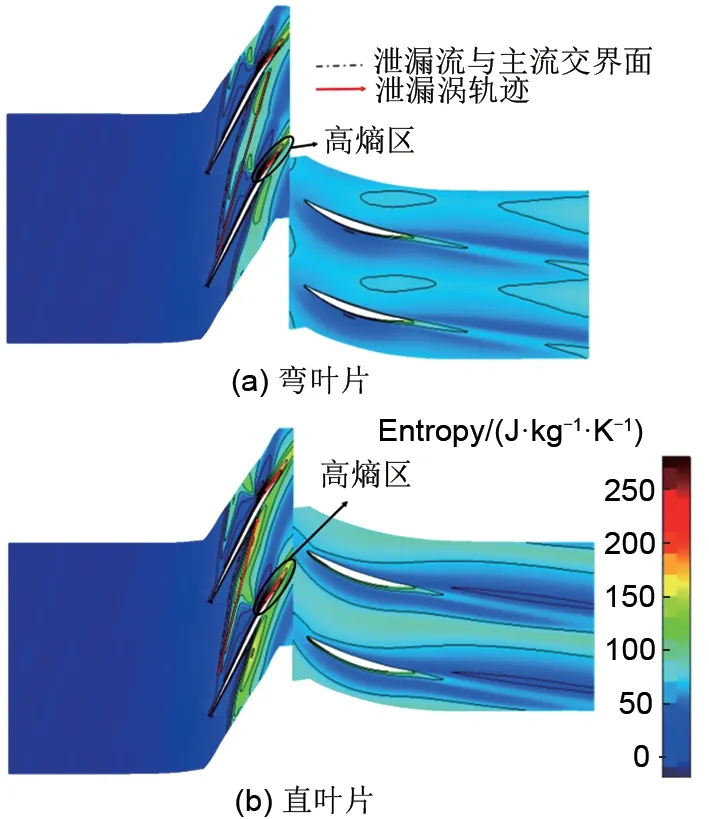
图9 设计工况点叶尖熵分布Fig.9 Entropy distribution near blade tip in design condition

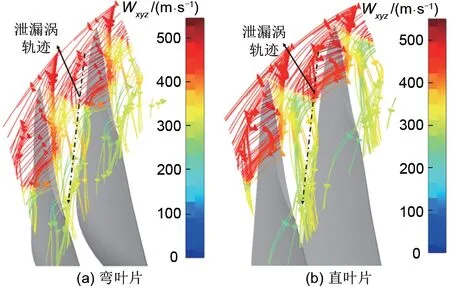
图10 设计工况点叶尖前缘间隙泄漏流Fig.10 Clearance leakage flow at leading edge of blade tip under design condition

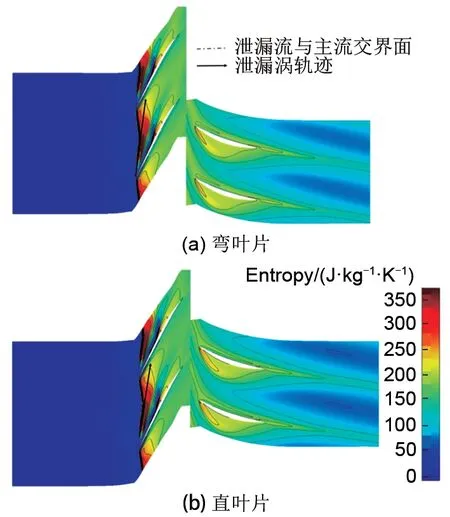
图11 失速点叶尖熵分布Fig.11 Entropy distribution near blade tip at stall point

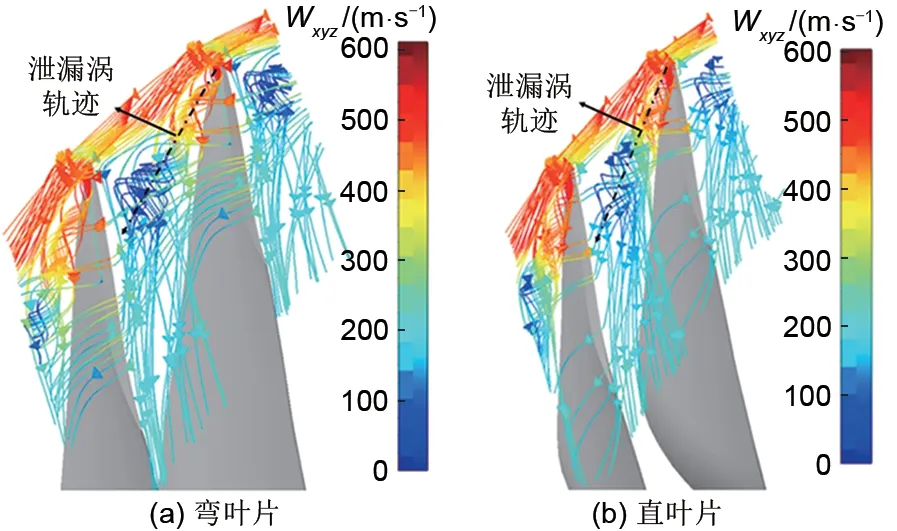
图12 失速点叶尖前缘间隙泄漏流Fig.12 Clearance leakage flow at leading edge of blade tip at stall point

3.4 弯叶片对进出口气流参数的影响

为进一步了解弯叶片对流场分布的影响，图13、图14对设计工况点和失速点动静叶入口径向速度沿叶展方向的分布情况进行比较。从图13左侧图可以看出，在设计工况下，同一叶展高度，当叶展高度低于0.08时，弯叶片产生的径向力使其径向速度小于直叶片，同时抑制低能流体向叶展中部迁移；当叶展高度在0.08～0.43的范围内时，弯叶片的径向速度大于直叶片；当叶展高度在0.43～0.83的范围内时，弯叶片的径向速度小于直叶片；当叶展高度大于0.83时，弯叶片的径向速度大于直叶片。采用弯叶片后，动叶入口径向速度变化范围减小。从图13右侧图可以看出，在同一叶展高度，弯叶片的静叶入口径向速度小于直叶片，径向速度的变化范围缩小，这有利于减小冲角变化范围，提高失速裕度，此时动叶与静叶的耦合效果良好。从图14可以看出，在失速点，对于动叶，除叶展高度在0.1～0.3的范围内，弯叶片的径向速度均小于直叶片。对于静叶，当叶展高度低于0.24时，弯叶片的径向速度小于直叶片；当叶展高度大于0.24时，弯叶片的径向速度大于直叶片。动静叶的径向速度变化范围缩小，这与弯叶片产生的径向力有关。

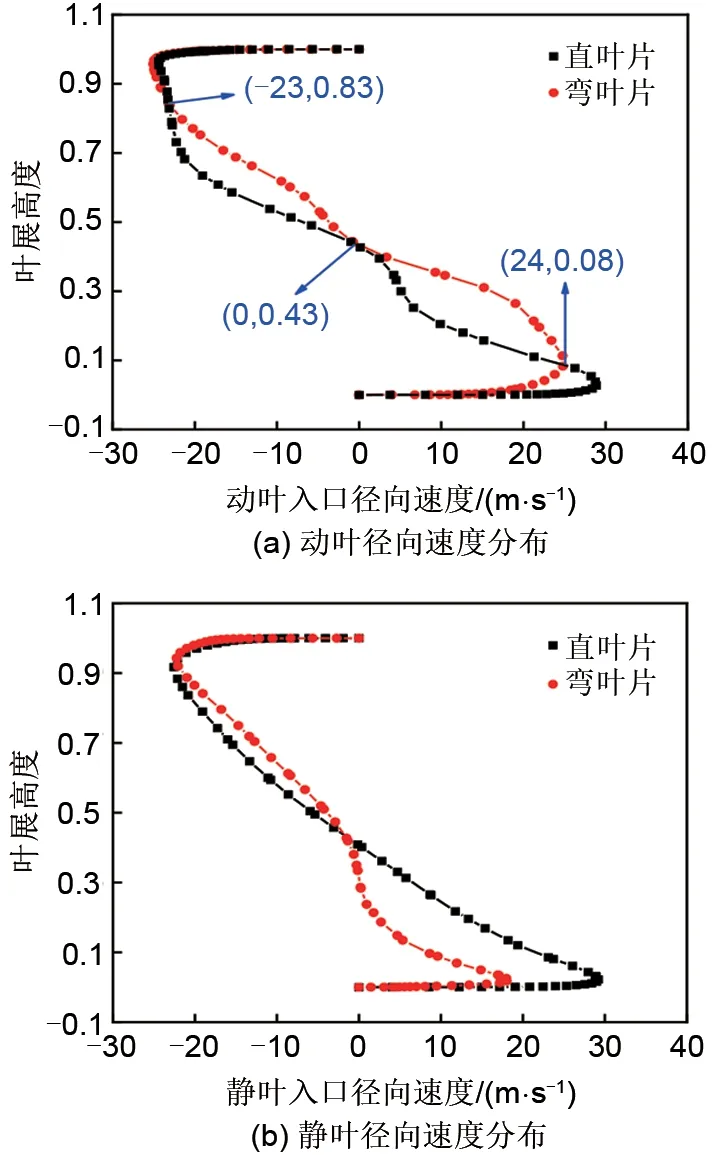
图13 设计工况下动静叶入口径向速度在叶展方向上的分布Fig.13 Distribution of inlet radial velocity of rotor and stator in spanwise direction under design condition

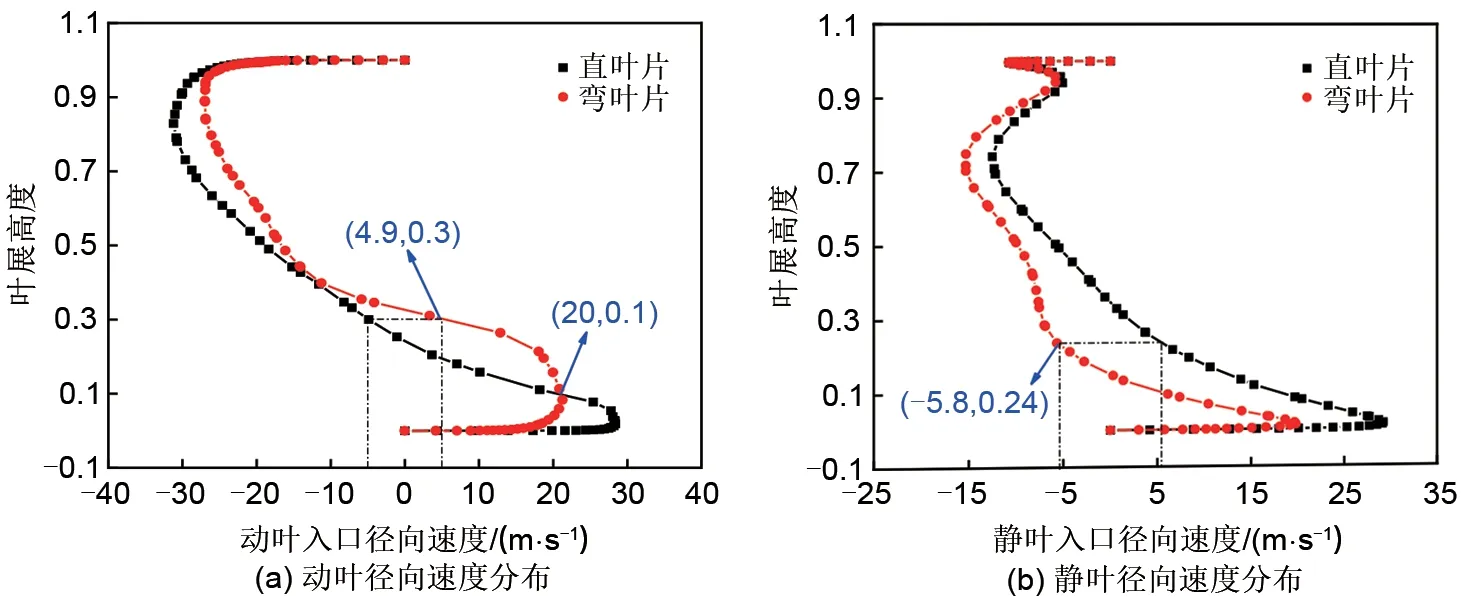
图14 失速点动静叶入口径向速度在叶展方向上的分布Fig.14 Distribution of inlet radial velocity of rotor and stator in spanwise direction at stall point

从图15可以看出，在设计工况下，采用弯叶片后，动叶叶根到叶展中部的出口气流角增加，叶展中部到叶尖的出口气流角减小，动叶出口气流角分布更加均匀；弯叶片的静叶出口气流角大致走势与直叶片相似，但是变化范围缩小。弯叶片可以使动叶及静叶的出口气流角在叶展方向分布更加均匀，这有利于增加失速裕度。从图16可以看出，在失速点处，采用弯叶片后，动叶出口气流角沿叶展方向的变化与设计工况下相似；静叶叶展中部及以上的出口气流角增加，大体走势与直叶片相同。采用弯叶片后，在设计工况与失速工况下，动叶及静叶的出口气流角分布都更加均匀。

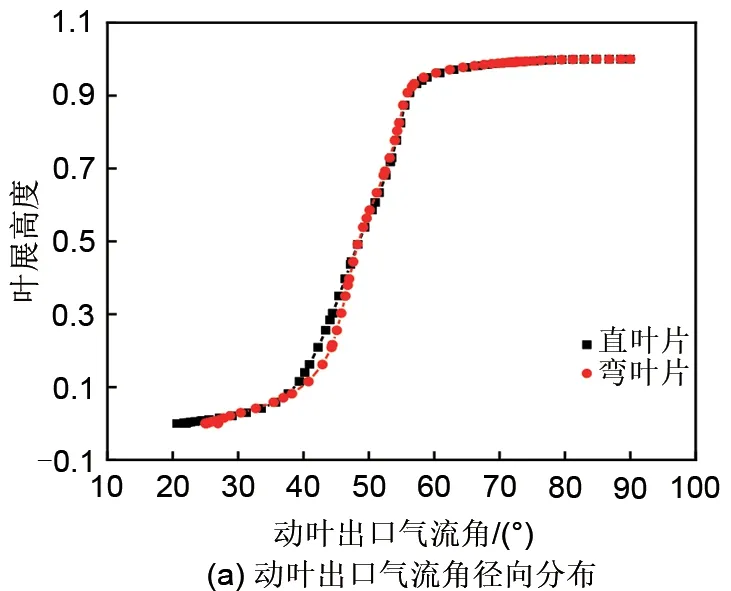
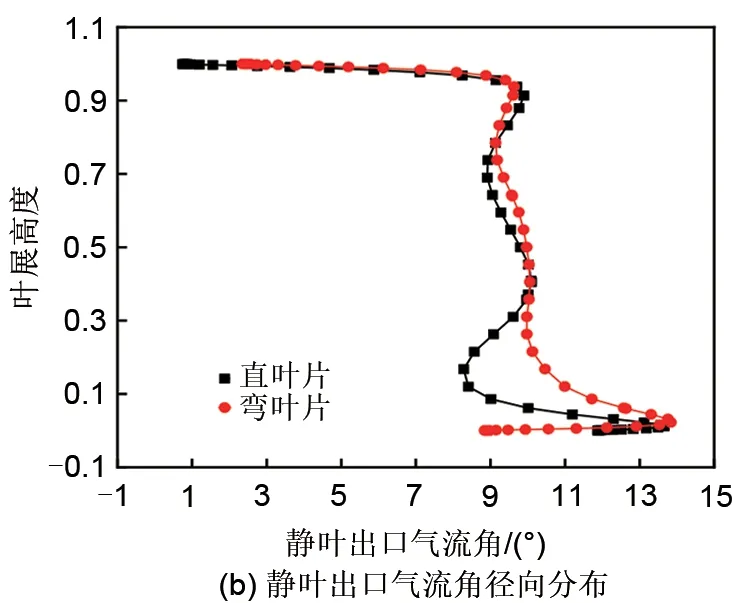
图15 设计工况下动静叶出口气流角径向分布Fig.15 Radial distribution of outlet flow angle of rotor and stator under design condition

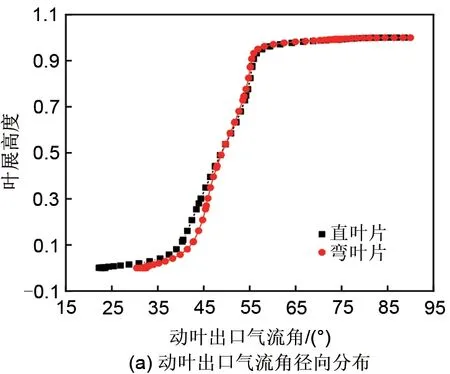
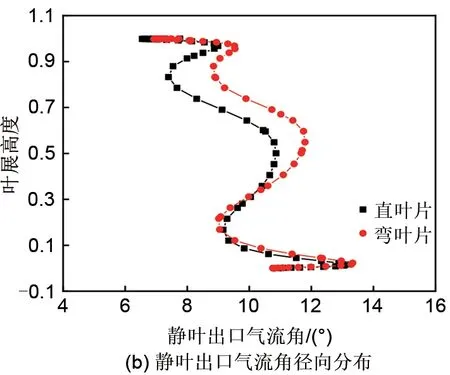
图16 失速点动静叶出口气流角径向分布Fig.16 Radial distribution of outlet flow angle of rotor and stator at stall point

采用弯叶片，气动载荷沿叶展方向分布更加均匀，抑制低能流体径向迁移，恶化叶根附近的流动情况，但是对叶展中部及叶尖附近是有利的。

3.5 弯叶片对激波结构的影响

从图17可以看出，设计工况下，在叶展根部，相比于直叶片，弯叶片吸力面尾缘角区分离更严重，这可能是导致峰值效率低于直叶片的原因。在叶展中部，采用弯叶片可以削弱激波强度，减小动静叶吸力面的附面层厚度，减弱激波与附面层的相互作用，从而优化叶展中部的流动情况。在叶尖处，采用弯叶片后，激波强度减弱，动叶与静叶尾迹区减小，激波与附面层相互作用的位置向下游移动。

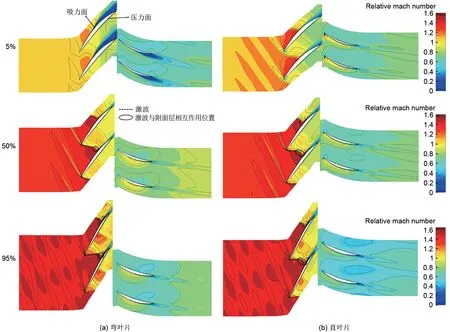
图17 设计工况下不同叶展高度对应的相对马赫数分布Fig.17 Relative Mach number distribution of different blade span under design condition

从图18可以看出，在近失速点，采用弯叶片后，动静叶叶根处吸力面的角区分离更加明显，静叶叶根吸力面前缘的激波消失，高马赫数区减小，静叶叶根前缘的流动情况得到改善。在叶展中部，采用弯叶片后，动静叶吸力面的附面层分离都有比较明显的减弱，激波结构与位置没有明显的变化。在叶尖处，采用弯叶片对附面层分离、激波结构没有明显的效果，这可能与失速的判定方法有关。

图18 失速点不同叶展高度对应的相对马赫数分布Fig.18 Relative Mach number distribution of different blade span at stall point

无论是在设计工况点，还是近失速点，采用弯叶片都会扩大叶展根部角区分离的范围，但是对于叶展中部和叶尖的流动情况是有利的，因为采用弯叶片后产生的径向力抑制低动量流体的径向迁移。在近失速点，无论是否采用弯叶片，在叶展中部和叶尖处都会形成相似的激波结构。

4 结 论

采用数值模拟的方法，以NASA Stage35为原型，通过正交试验法研究不同动静叶之间弯高、弯角之间的耦合关系，并对其进行优化，得出以下结论。

（1）通过极差分析选取动叶弯角为30°、动叶弯高为0.4、静叶弯角为10°、静叶弯高0.3的组合为最优组合，其失速裕度增加60.56%，效率及压比降低幅度均在可接受范围内。

（2）采用弯叶片能增加单级压缩机的失速裕度，最大增加了60.56%，但是会减小峰值效率与最大压比，峰值效率最多减小6.54%，最大压比最多减小8.41%。对于动叶，与前弯相比，同样角度的后弯会带来更大的损失。

（3）采用弯叶片虽然会恶化叶根附近的流动情况，但是可以使叶展载荷分布更加均匀，改善叶展中部及叶尖附近的流动情况，弱化激波强度，削弱激波与附面层的相互作用，延迟动叶叶尖泄漏涡与主流的交界面到达叶尖前缘，从而提高单级失速裕度。

符号说明

c—— 叶片弯高

CAES—— 压缩空气储能系统

EI—— 峰值效率增量，%

f—— 分数因子

Mi—— 试验因素取水平i时，数值模拟结果的平均值

PI—— 最大压比增量，%

R—— 各试验目标平均值M的极差

SM——失速裕度，%

SMI—— 失速裕度增量，%

α—— 叶片弯角，(°)

下角标

1—— 动叶叶片

2—— 静叶叶片