双悬臂轴系结构通过临界转速时振动实验研究

胡东旭 ，王欣然 ，李文 ，戴兴建 ，王星 ，侯虎灿 ，陈海生 ,3，左志涛

（1中国科学院工程热物理研究所，北京 100190；2中国科学院大学，北京 100049；3中科南京未来能源系统研究院，南京 江宁 211135；4毕节高新技术产业开发区国家能源大规模物理储能技术研发中心，贵州 毕节 551712）

作为旋转机械中最具有代表性的机组之一，膨胀机和压缩机是压缩空气储能(CAES)系统的关键部件。为了满足变工况、低功耗等要求，膨胀机、压缩机组多采用双悬臂轴系结构，这种结构形式具有高效率和高性能等优点，因此，除了压缩空气储能外，其还广泛应用于化工、石油、空分等领域，是现代工业尤其是能源行业的核心设备和关键性技术，是一个国家实现工业现代化的重要体现[1-5]。当前很多能源领域的高端齿式膨胀机组、压缩机等仍然由国际工业巨头掌握和控制。尽管国内制造企业在对引进技术进行消化、吸收的基础上，已具备一定的研发与生产能力，但与国外先进水平仍然存在较大差距。

在众多技术难题中，稳定性和振动问题尤为突出。国内复杂齿式多轴耦合转子系统动力学特性的研究起步较晚，仍有很多科学问题有待研究。蒋庆磊等[6-8]探究了齿轮啮合转子系统的建模方法，并研究了齿轮啮合作用对系统固有特性的影响。庞辉等[9]建立并求解了多轴系齿轮转子耦合系统的振动方程，获得了耦合转子系统的振动模态和不平衡响应，发现齿轮啮合作用会使轴系产生新的振型，同时还发现提高高速轴的平衡精度对于提高轴系的稳定性有积极意义。朱丽莎等[10]、车永强等[11]的分析表明，因齿轮传动导致的轴系间耦合作用会明显影响轴系的振动。Gao等[12]在综合考虑了传动误差、齿侧间隙和时变啮合刚度的基础上，研究了滚动轴承与滑动轴承联合支撑下齿轮啮合转子系统的动力学特性。Zhang等[13]通过对五轴齿式压缩机模型的有限元分析，指出轻载时振动正常的轴系可能由于载荷的增加而出现振动问题。张明[14]通过公式推导建立了转子临界转速与轴承支承刚度之间的关系，揭示了整体齿式压缩机的临界负荷故障机理。刘宾宾[4]利用电磁执行器模拟齿轮耦合复杂系统中齿轮啮合造成的径向轴承负荷变化，研究了不同载荷下齿轮转子耦合复杂系统的动力学特性和不平衡响应规律。

尽管有不少学者针对齿轮啮合双悬臂轴系的动力学特性开展了研究工作，但是还存在一些不足，尤其是缺乏对双悬臂结构通过临界转速时详细振动特性的实验研究。本文基于某型号真实的双悬臂膨胀机轴系结构，开展了针对该轴系尤其是高速轴振动特性的实验研究。通过多次升降速实验，重点分析了高速轴的振动幅值曲线、振动频谱、伯德图和振动能量分布频谱图等，确定了该转子的临界转速，并探究了通过临界转速时不同升速方案对振幅的影响，获得了一些量化的实验结论，可以为日后类似轴系结构的设计和运行提供借鉴。

1 研究对象

本文实验的研究对象为压缩空气储能领域膨胀机和压缩机最为常见的双悬臂轴系结构，实验件的最大传递功率为10 MW，输入转速为4500 r/min，低速轴设计转速为8300 r/min，高速轴设计转速为17500 r/min。图1为实验件结构图，实验件低速轴为刚性转子，高速轴为柔性转子，即设计转速在一阶临界转速之上，该结构的振动特性具有影响因素多、振幅变化敏感、设计难度大等特点。因此本文以该轴系为研究对象，重点分析了高速轴过临界时的振动特性。

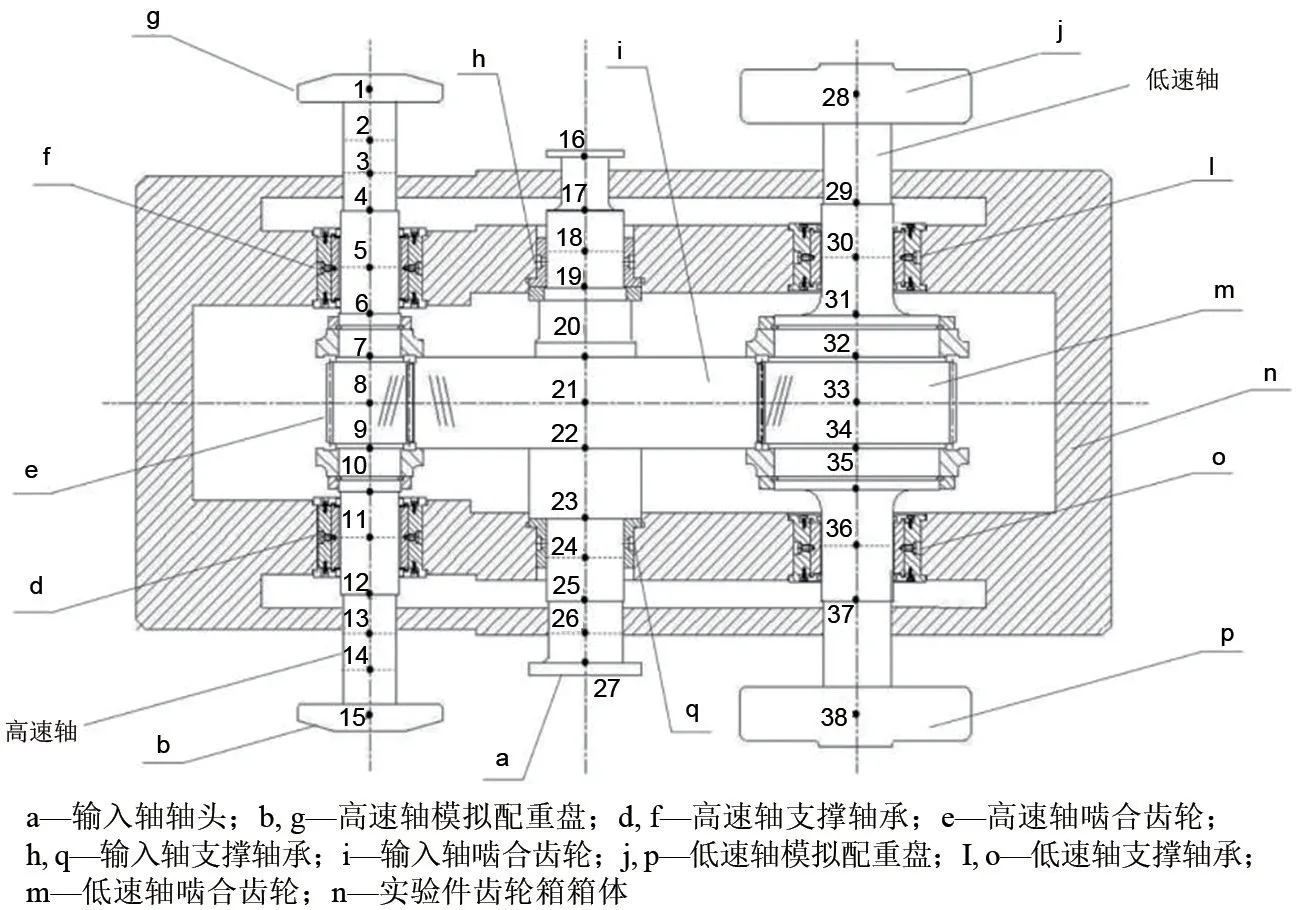
图1 实验件结构图[15]Fig.1 Structure of test piece[15]

2 研究方法

2.1 研究内容

本文主要采用实验方法开展了双悬臂轴系结构的动力学特性探究，重点针对柔性的高速轴动力学特性进行了分析。首先分析了轴系振动值随速度的变化曲线，确定了在振动峰值对的应转速；之后，通过进一步分析轴系的伯德图、振动能量分布频谱图等，证实了产生振动峰值的原因是在升速过程中存在着临界转速；最后，分析了升速连续性和升速时间对振动的影响。

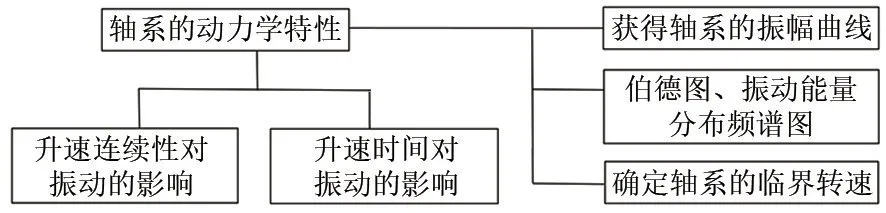
图2 研究内容Fig.2 Main research contents

2.2 实验平台

本文中的动力学测试平台由动力系统、控制系统和测振系统等几部分组成。动力系统最大功率315 kW，最大扭矩1010 N·m。控制系统包括电机转速控制和供油控制，电机转速可以在300～3000 Hz内连续调节，动力系统增速箱最高输出转速45000 r/min，供油压力可以在0～1 MPa内连续调节，最大供油量400 L/min。测振系统主要有振动探头、前置器、硬件处理模块和软件分析系统等组成，能够测量实验件振动的位移、速度和加速度等信息，并通过软件分析系统获得转子的极坐标图、轴心轨迹图、振动频谱图、瀑布图和伯德图等详尽的振动信息。本测试平台中，最为核心的部件为测振系统，电涡流振动探头的灵敏度为8.78 V/mm。振动加速度探头其最大可测量50 g峰值振动，灵敏度为100 mV/g。速度探头的灵敏度为每秒3.94 mV/mm(波动范围为±5%)，测量振动速度最大值为1270 mm/s。振动处理器采用本特利3500模块，精度为满量程的±0.33%。

3 结果分析

3.1 动力学特性分析

3.1.1 振动随速度变化规律

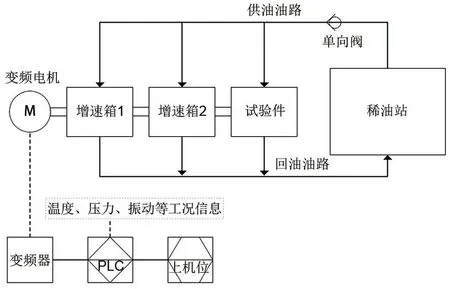
图3 实验系统流程图Fig.3 Experiment system

图4 实验系统主体结构Fig.4 Experiment system

实验中，高速轴转子在14000 r/min左右出现了振动峰值，为了验证振动峰值出现是否具有偶然性，在14000 r/min附近进行了4次升降速实验，升降速曲线如图5所示。在4次升降速过程中，转速的变化范围均为8000～17600 r/min，首先转子从8000 r/min升速至12000 r/min，停留1 min后，分别以20、30、40和50 s不同的升速速度加速到16000 r/min，停留1 min后，继续提升转速至17600 r/min，运行1 min后开始降速。

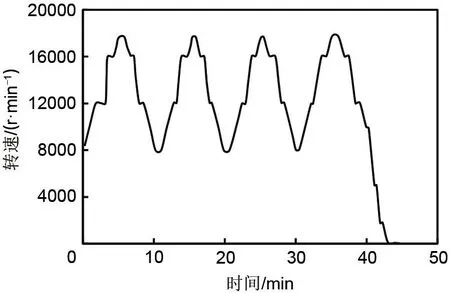
图5 四次升降速曲线Fig.5 Quartic acceleration and deceleration curve

图6给出了升降速过程转子振动曲线，由图可以看出，每次升降速的振幅变化趋势基本相同。在升速阶段，当转速达到12000 r/min后，振动开始缓慢升高，1 min内振动值从12μm提高到20μm左右；若继续提高转速，则振动值可以在15 s内从20μm提高到50μm以上，并在14200 r/min左右达到最高值；此后随着转速升高后振动值又骤然降低，在15 s内从50μm以上降低到20μm以下，而后随着转速提升，振动值有缓慢提升。在从12000 r/min到16000 r/min的4次升速过程中振动峰值逐渐从52μm提高到61μm，这是因为4次升速过程中的升速时间从20 s到50 s逐次增长，能量累积也逐渐增大，导致振动峰值也逐次提高。图7给出了高速轴和低速轴振动幅值对比，从中可以看出，低速轴无明显的振动峰值，但在在高速轴振动出现峰值时，低速轴振动也从28μm增加到了33μm，可见此时高速轴的振动值对低速轴的振动产生了一定的影响。初步判断在14200 r/min左右，高速轴存在临界转速，下文将通过进一步更详细的振动分析来验证该判断。

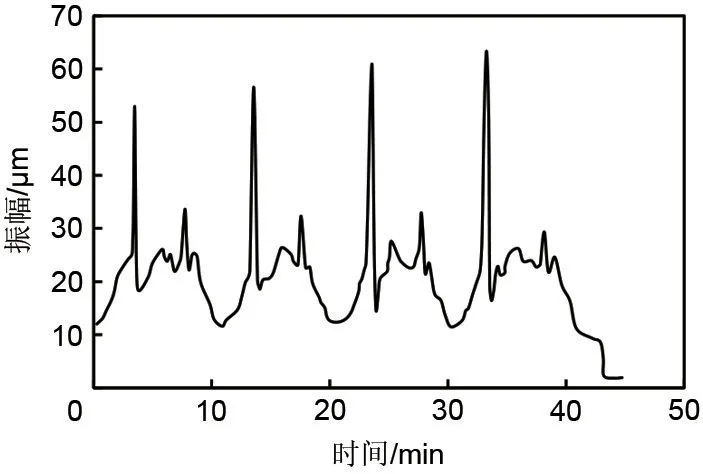
图6 升降速过程转子振动曲线Fig.6 Amplitude of rotor vibration during speed up and down

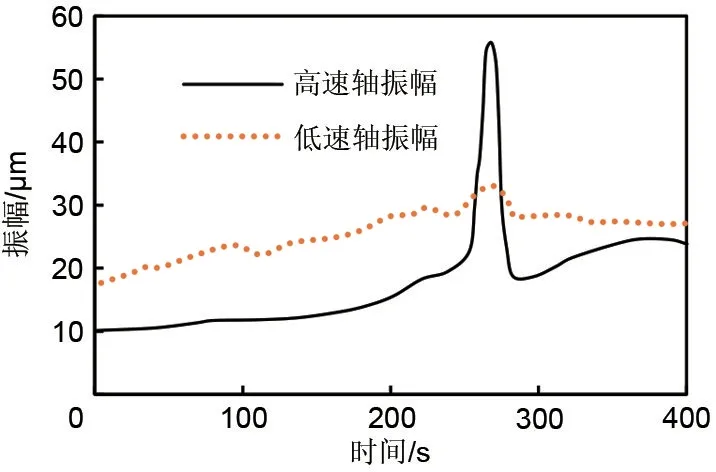
图7 高速轴和低速轴振动幅值对比Fig.7 Vibration amplitudes of high speed shaft and low speed shaft

首先分析通过14200 r/min时转子的振动变化规律，图8给出了升速过程曲线，转子从12000 r/min直接升速到15500 r/min，升速时间为60 s。图9给出了该升速过程中转子振动的变化规律。由图可知，在转速由12000 r/min升到14200 r/min过程中，尽管只经历了30 s，但是振幅迅速由22μm升到66μm，当转速继续升高到15500 r/min时，振幅值又迅速降低到20μm以下，该振动现象符合轴系过临界转速时的振动特征。结合图8和图9还可以看出，振动峰值对应转速前后的共振区域范围分别约为15%和9%，可见对于本文的研究对象，振动峰值前的共振区域要大于振动峰值之后的共振区域。

分别取过量的Lut、Lut-PC、Lut-SD和Lut-PC- SD加入到蒸馏水中，于25 ℃条件下恒温摇床法平衡48 h，水膜滤过，取续滤液进HPLC测定其表观溶解度。结果见表1。2种固体分散体均可极显著性提高Lut的溶解度（P＜0.01）。其中，Lut-SD将Lut的溶解度提高至5.98倍，Lut-PC-SD则将Lut溶解度提高至6.57倍。Lut-PC-SD的溶解度与Lut-SD和Lut-PC相比，Lut的溶解度有进一步的提高（P＜0.01）。

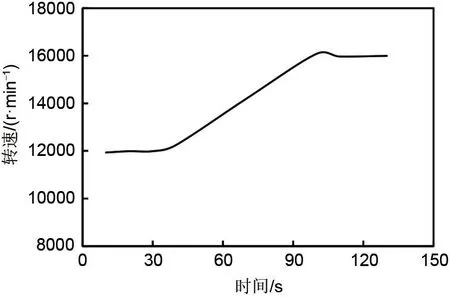
图8 转子升速曲线Fig.8 Rotor speed up curve

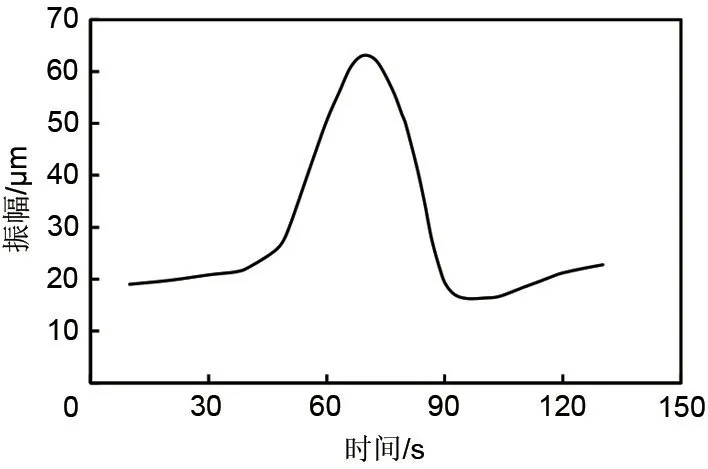
图9 升速过程中振幅变化曲线Fig.9 Amplitude curve during speed up

图10给出了转子在远离振动峰值转速和振动峰值转速时的振动频谱图。在不同转速下，一倍频振幅始终占据主导位置，但是在振动峰值时，一倍频占据的比例显著提高。在10800 r/min时，1倍频的振幅达约为6μm，其中0.5、2和4倍频也分别有2～3μm的振幅。当转速达到14200 r/min时，1倍频振幅达到了52μm，增长了将近9倍，0.5倍频振幅为4μm，其它倍频振幅均在3μm以下，增长幅度不及一倍频增长幅度的5%。可见，在转子转速接近14200 r/min时，1倍频振幅会剧烈增加，其它倍频的振幅也会有增加，但是增加的幅度远小于1倍频的增加幅度。

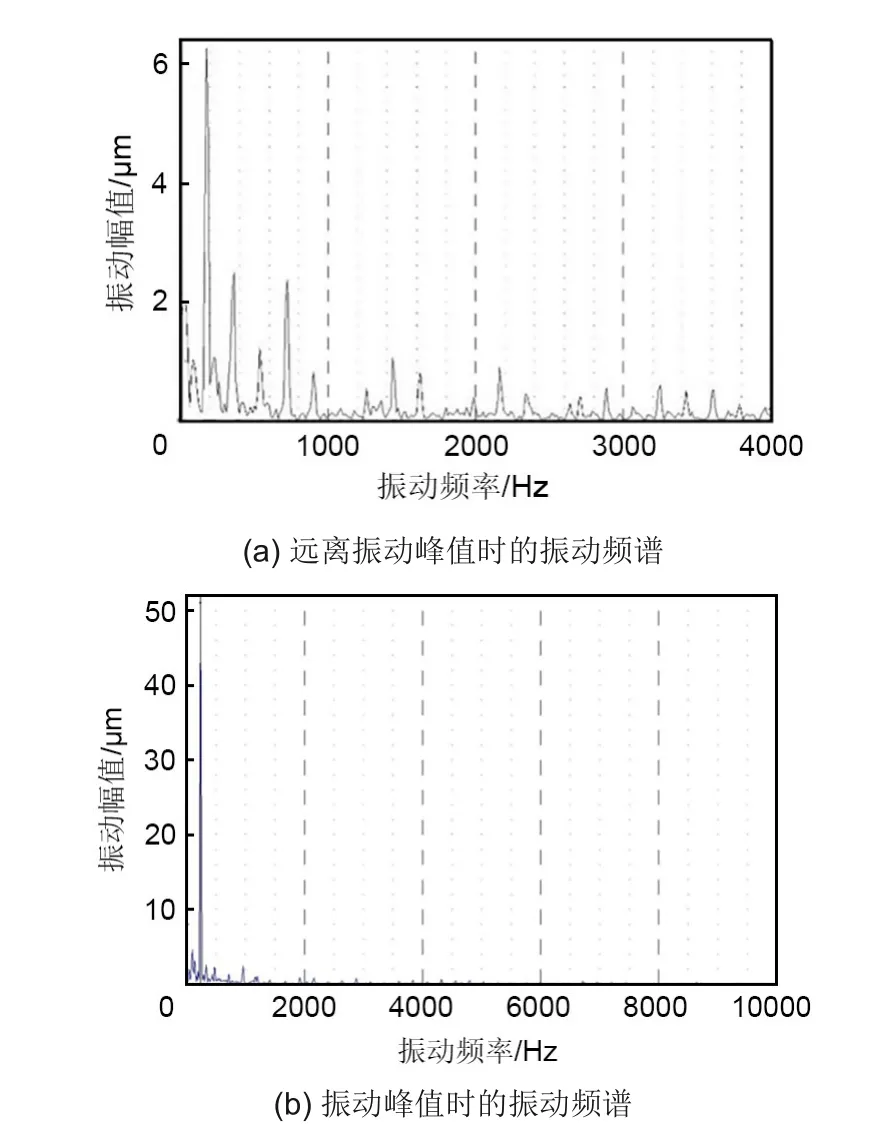
图10 不同转速下的振动频谱图Fig.10 Vibration spectrum at different speeds

3.1.2 临界转速确定

图11给出了转子振幅和相位角随转速变化曲线(伯德图)。从图中可以看出，从10000 r/min提速到16000 r/min过程中，相位角变化了180°以上，而且在14200 r/min左右出现了明显的振动峰值，表明转子完全地跨越了14000～14500 r/min附近的临界转速，即转子在14000 r/min左右存在临界转速。

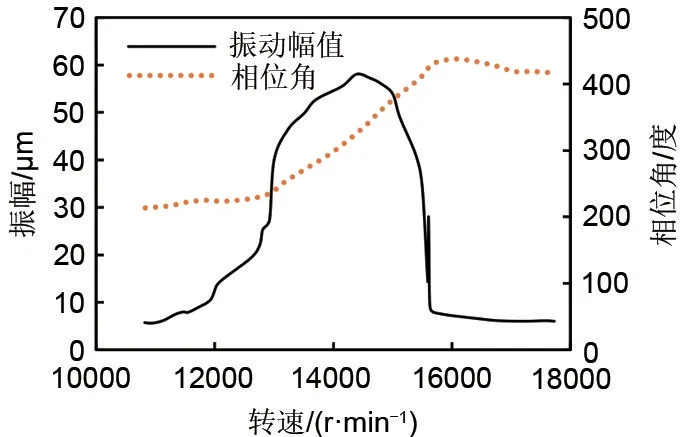
图11 转子振幅、相位角随转速变化曲线Fig.11 Variation curve of rotor amplitude phase angle with speed

图12给出了转子运行时的振动能量分布频谱。图中椭圆范围内一倍频斜率曲线和转速交点位置存在着明显的能量累积(交点大小表明能量的大小)。从而可知，转子振动的主要能量来源为一倍频，且主要集中在12000～16000 r/min之间，即14000 r/min转速附近，进一步验证了该转速范围内存在着临界转速，这与之前的分析和判断是吻合的。

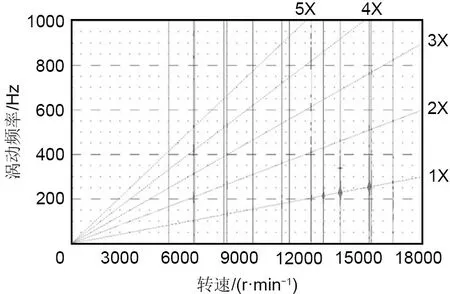
图12 高速轴振动能量分布频谱Fig.12 Vibration energy distribution spectrum

图13给出了转子振动的频谱瀑布图(级联图)，从中可以更加直观地看出，一倍频为转子的主要振动频率，且箭头所指位置为振动峰值，此时的对应转速为14200 r/min。由此可以完全确定，该转子在14200 r/min左右存在临界转速。

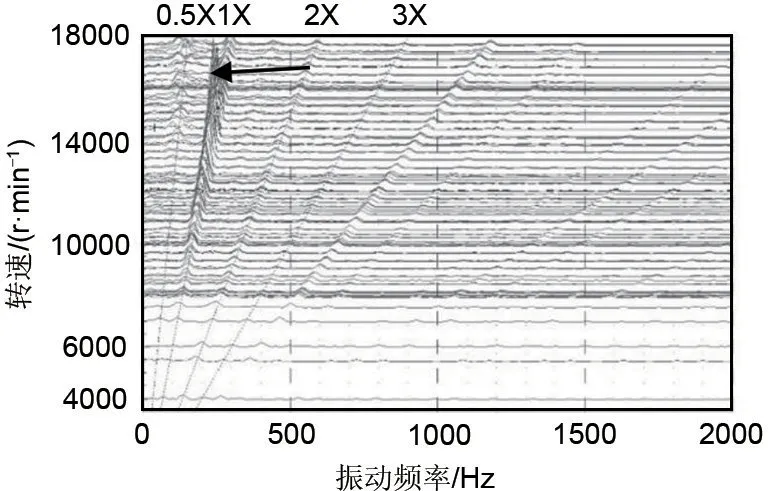
图13 高速轴频谱瀑布图Fig.13 Spectrum waterfall

3.2 升速过程对振动影响

3.2.1 升速连续性对振动的影响

在压缩机、膨胀机实际运行时，由于机组设计要求、现场条件不同等原因，运行时往往采用不同的升速策略。本文采用线性连续升速和阶梯升速两种方案，比较了两种不同升速方案情况下，转子通过临界转速时的振动变化情况。表1给出了两种升速方案的详细信息。

表1 升速过程设置Table 1 Speed up process setting

图14给出了两种不同的通过临界转速的方案。方案一中转速直接由12000 r/min提速到16000 r/min，提速时间为60 s，转速加速度为4020 r/s2。方案二中转速首先由12000 r/min提升到13000 r/min，提速时间为30 s，并停留了约20 s，之后转速由13000 r/min提速到15500 r/min，用时30 s，转速加速度为7020 r/s2。

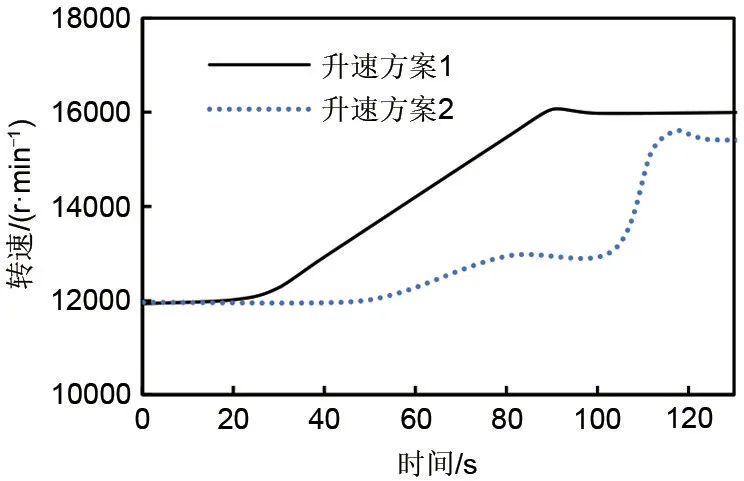
图14 两种不同方案的升速曲线Fig.14 Acceleration curves of two different schemes

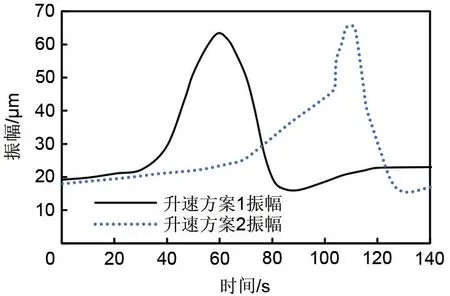
图15 两种升速方案的振幅对比Fig.15 Amplitude comparison of two speed up schemes

3.2.2 升速时间对振动的影响

理论上，通过临界转速时，升速越快，振动峰值越低，但是受到动力条件和其它一些因素的影响，转速提升的速度会受到制约。因此本小节将探究通过临界转速时，升速时间对转子振动幅值的影响。

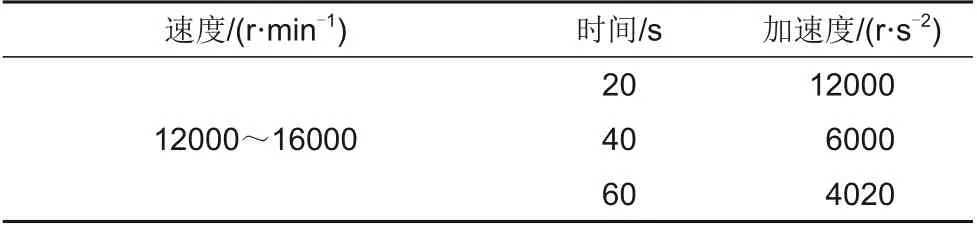
表2 升速时间/加速度设置Table 2 Acceleration setting

图16给出了过临界转速时，3种不同提速方案下的振幅曲线。从12000 r/min到16000 r/min的提速时间分别为20、40和60 s，转速加速度分别对应12000、6000和4020 r/s2。从图中可以看出，提速时间从20 s延长到60 s时，振动峰值从51μm增加到61μm，提升了约20%，而且振动幅值的提升近似线性。

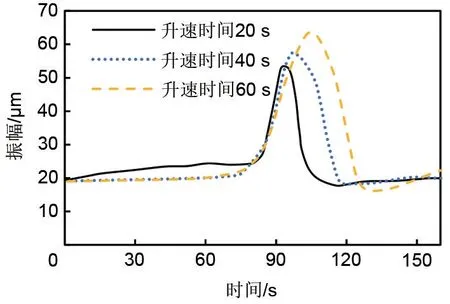
图16 提速时间对振幅影响Fig.16 Influence of speed increase on vibration amplitude

4 结 论

本文针对某传递功率为10 MW的双悬臂轴系结构进行了动力学特性实验研究，重点分析了该轴系高速轴的振动幅值曲线、振动频谱和振动能量分布频谱图等，确定了转子临界转速值，并探究了不同升速方案对转子通过临界转速时振幅的影响。最终得出以下结论。

（1）获得了CAES叶轮机械典型双悬臂轴系转子动力学特性：转子转速接近临界转速时，1倍频振幅会剧烈增加，其它倍频的振幅也会有增加，但是幅度远小于1倍频的增加幅度。高速轴在14200 r/min左右存在临界转速，临界转速前的共振区域约为15%，临界转速后的共振区域约为9%，临界转速前的共振区域比临界转速后的共振区域要大约6%。接近临界转速时，1倍频振幅从6μm增加到了52μm，增加了46μm；其它倍频的增长幅度均在2μm以下，不及一倍频增长幅度的5%。

（2）本研究获得了升速连续性对轴系振动的影响特征：轴系升速通过临界转速时，应该快速连续性通过，阶梯式的升速方案对振动不利。方案一转速直接由12000 r/min提速到16000 r/min，提速时间为60 s，转速加速度为4020 r/s2。方案二从12000 r/min提升到13000 r/min停留20 s后继续升速到设定转速，通过临界转速的加速度为7020 r/s2。尽管通过临界转速时方案二的速度加速度更快，但是由于其在临界转速附近有停留，造成了振动能量累计，使得最终的方案二的振动峰值反而大于方案一。

（3）本研究也获得了升速时间对轴系振动的影响特征：通过临界转速时，振动峰值会随着提速时间的延长而近似线性增加，当提速时间从20 s延长到60 s时，加速度分别对应12000、6000和4020 r/s2，此时振动峰值从51μm增加到61μm，提升了约20%。