基于经济模型预测控制的多虚拟电厂两阶段协调优化调度

孙乐平，韩 帅，吴宛潞，郭小璇

（广西电网有限责任公司电力科学研究院，广西 南宁 530023）

2021年3月15日，习近平总书记提出要构建以新能源为主体的新型电力系统。新能源发电具有天然的间歇性和波动性，其大规模并网必将加剧电源供给和负荷需求的不平衡。虚拟电厂(virtual power plant，VPP)技术为解决此类问题应运而生。VPP利用先进的通信技术，可将不同地域的新能源联系在一起，通过协调优化调度策略，使得出力不稳定的新能源在电力市场竞价中保有一定的竞争力[1]。

针对VPP内部优化调度和多VPP竞价已有相关的研究。文献[2]通过改进随机规划模型，构建含风电等不可控能源及储能的VPP市场竞标策略。文献[3]通过整合储能设备、不可控分布式能源及可控电源，构建了平衡市场和日前市场的VPP购售电模型。文献[4]考虑到风电出力的不确定性，建立多VPP参与电力市场日前交易模型。文献[5]运用同步交替方向乘子法，建立了多VPP分散式协调调度模型。单VPP内部优化调度问题，并未考虑其他VPP决策给自身调度策略带来的影响；多VPP的研究主要考虑的是协调优化调度，使得经济效益最高，但是并未关注弃风、弃光的问题。

针对日前日内两阶段优化调度的研究，文献[6]构建了日前日内两阶段优化调度模型，但是日内调度仅仅考虑了各电源调整出力时的附加成本，日前日内两阶段调度间的联系紧密性较差。文献[7]基于模型预测控制(model predictive control，MPC)构建实时调度模型，但是缺乏日前调度结果的引导，优化结果难以实现全局最优。文献[8]将滚动优化运用到日内优化调度中，但缺少反馈校正环节，难以保证调度精度。

针对VPP内部新能源出力不确定性，为降低其功率波动的影响通常采用鲁棒优化、随机优化等方法予以应对。文献[9]采用随机规划的方法对不确定性进行处理，不确定参数在有限场景下很难反映变量的真实情况，其决策对潜在的风险规避能力相对较弱。文献[10]基于鲁棒经济优化模型，利用多面体不确定集来应对新能源出力的不确定性，场景的缩减和优化技术在很大程度上决定了随机优化过程的繁简，且鲁棒优化下的调度方案比较保守。文献[11]在考虑鲁棒性的基础上，进一步使用了MPC去构建消纳大规模光伏的优化调度方案。可见，单次求解含新能源的优化调度问题，鲁棒性难以评价的同时，偶然性也较大。

本文在消纳风电的前提下，首先构建了多VPP参与的非合作博弈日前市场优化调度模型，然后在文献[11]传统MPC的基础上设计了改进经济模型预测控制(economic MPC，EMPC)，基于EMPC对多VPP日前日内两阶段进行优化调度，弥补日前预测的偏差。该调度模型具有两个创新点：一是基于区间预测技术，设计自适应域步长MPC以改进文献[11]中固定步长MPC，减小了相似日选取带来的误差，同时将自适应域步长MPC引入由纳什最优决策形成的多VPP日前调度策略中；二是日内调度实时反馈校正考虑了经济性，弥补了传统日内调度仅关注功率偏差而忽略经济性的不足，使得日内优化经济性更强。总之，本文通过日前自适应滚动优化保证了VPP运行经济性，结合日内动态反馈调整进一步消除了风电出力不确定性的影响，验证了多VPP多时间尺度两阶段调度模型的有效性。

1 多VPP运行目标函数及约束条件

新能源发电固有的间歇性和波动性，极易打破VPP内部电力供需平衡，即单个VPP不同时间段存在一定的电量盈余或缺额。通过合理的优化调度策略，并在各VPP间签订双边交易合同，可将多VPP系统内缺电VPP和多电VPP进行整合，优化各VPP间的交易电量，提高多VPP系统的调度灵活性，从而实现多VPP的整体收益最大化。本研究假设每个VPP内电源均包含风机、燃气轮机和储能设备，电负荷包括基础负荷及可中断负荷，用电高峰时，VPP在向用户提供一定补偿的前提下，切除可中断负荷达到削峰的效果。

1.1 目标函数

多VPP系统优化调度以最大化利润为目标，目标函数为

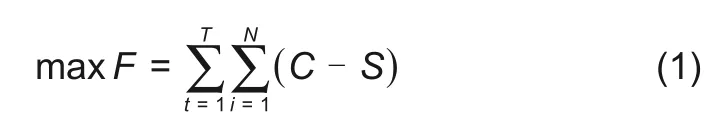
式中，F为利润；C和S分别为收益和成本；N为联合系统中VPP的个数；T为调度的时间段。

式(1)表明，多VPP系统运行利润F是由收益C扣除成本S得到的，其中C由t时段第i个VPP负荷收益Ct,L,i、电力交易收益Ct,E,i、储能充放电收益Ct,ES,i组成；S由t时段第i个VPP燃气轮机、风机的运维成本St,GT,i、St,WPP,i组成，即

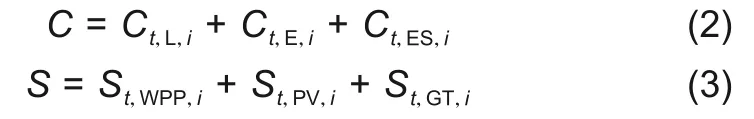
每部分具体表达式如下。（1）负荷收益Ct,L,i

负荷收益由总负荷收益和可中断负荷补贴给用户的成本组成，负荷收益可表示为

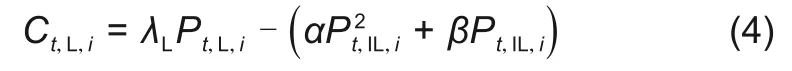
式中，Pt,L,i、Pt,IL,i分别为t时段第i个VPP总负荷和可中断负荷功率；α、β为可中断负荷补偿成本的二次系数、一次系数。

（2）电力交易收益Ct,E,i

电力交易收益包括与大电网交互功率收益和VPP间交易收益

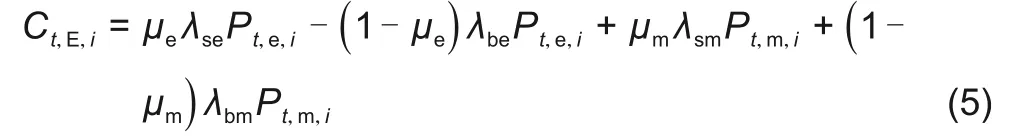
式中，Pt,e,i、Pt,m,i分别为t时段第i个VPP与大电网交互功率、与其他VPP间交易功率，售电为正，购电为负；μe、μm为0-1变量，1表示售电，0表示购电；λse、λbe为与大电网售电、购电价格；λsm、λbm为VPP间售电、购电交易电量。

（3）储能设备收益Ct,ES,i

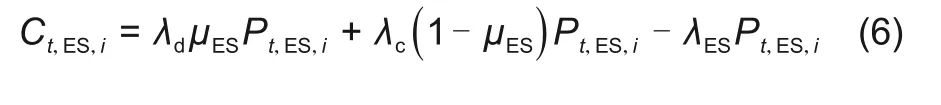
式中，Pt,ES,i为t时段第i个VPP储能设备充放电功率，充电为正，放电为负；μES为0-1变量，1表示充电，0表示放电；λd、λc分别为充放电电价；λES为储能设备折旧补偿系数。

（4）燃气轮机成本St,GT,i

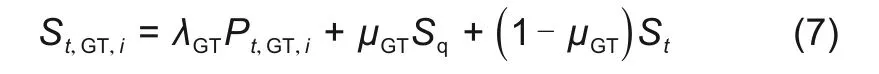
式中，λGT为燃气轮机运维成本系数；Pt,GT,i为t时段第i个VPP燃气轮机出力；Sq、St为启机、停机成本；μGT为0-1变量，1表示启机，0表示停机。

（5）风机运维成本St,WPP,i

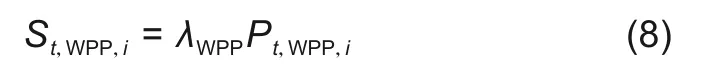
式中，Pt,WPP,i为t时段第i个VPP风机功率；λWPP为风机运维成本系数。

1.2 运行约束条件

VPP运行约束条件应包括等式约束和不等式约束。

（1）各VPP功率平衡约束

线路安全约束涉及节点电压及传输功率上下限约束，其约束条件请参考文献[12]，受篇幅限制，此处不再重复。

2 多VPP日前日内协调优化调度模型

为实现对多VPP内分布式电源、可中断负荷的有效控制，同时考虑风电出力的不确定性，本节拟提出一种自适应域长度的EMPC来完成VPP多时间尺度两阶段经济优化调度，如图1所示。可见本研究提出的基于EMPC优化调度方案分为日前滚动优化与日内实时反馈两个阶段。

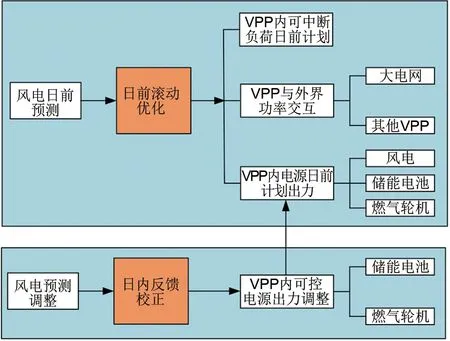
图1 两阶段VPP优化调度策略Fig.1 Two-stage VPP optimal scheduling strategy

2.1 自适应域长度日前两阶段滚动优化

对于日前多VPP优化调度，目标函数为多VPP系统利润最大，以预测域Nft内的风电出力点预测值作为滚动优化条件，考虑多VPP系统的约束条件，利用EMPC滚动优化模型生成日前调度计划，多VPP日前优化调度模型如图2所示。为降低风电预测误差的影响，预测域步长随风电预测误差自适应动态调整，保证优化结果的鲁棒性。优化控制变量包括：储能设备出力状态、燃气轮机出力和VPP与大电网、多VPP间联络线交互功率及参与需求响应的可中断负荷。

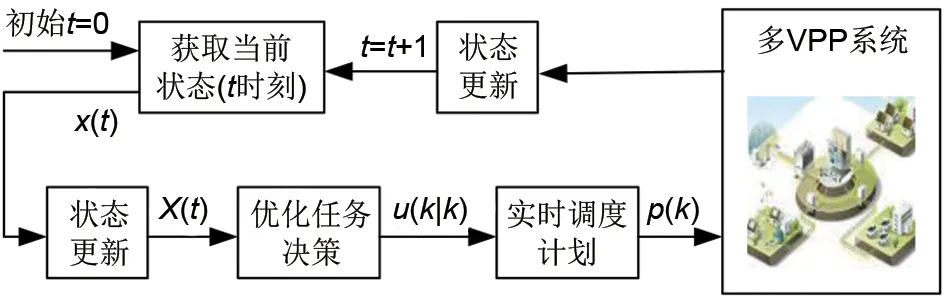
图2 日前优化调度模型Fig.2 Day-ahead optimized scheduling process

2.1.1 日前调度滚动优化过程

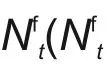
在EMPC架构下，多VPP联合系统的状态需由所有VPP的状态共同确定，由于各VPP状态方程相互独立，假设gi为第i个VPP的状态方程，则联合系统状态可描述为

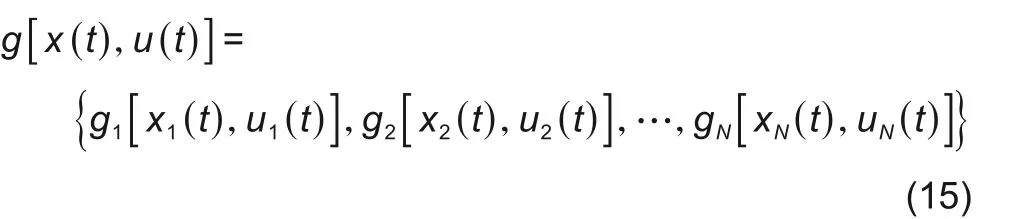
进一步，联合系统的利润函数可以分解为

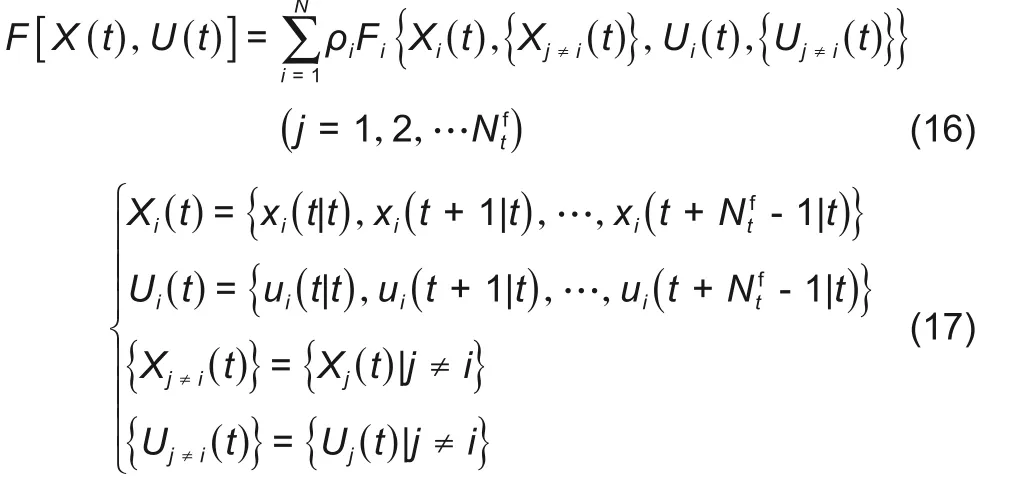
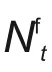
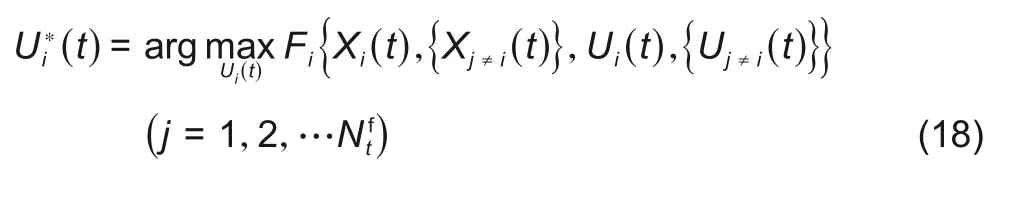
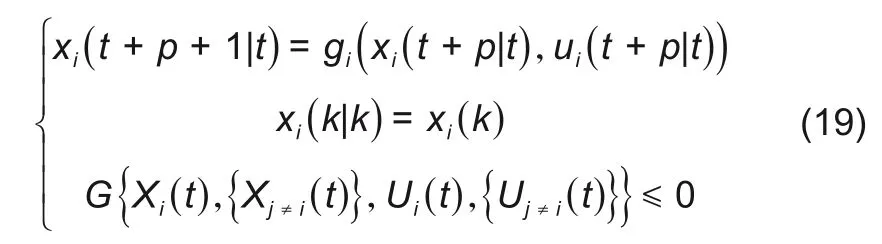
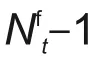
在确保网络通信畅通的前提下，联合系统内各VPP间可充分交换信息，通信网络可提供其他VPP的状态{xj≠i(t)}和控制输入{Uj≠i(t)}，故优化问题的计算量将极大减少，通过求解该优化问题即可得第i个VPP的控制输入。

2.1.2 基于非合作博弈迭代求解

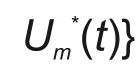
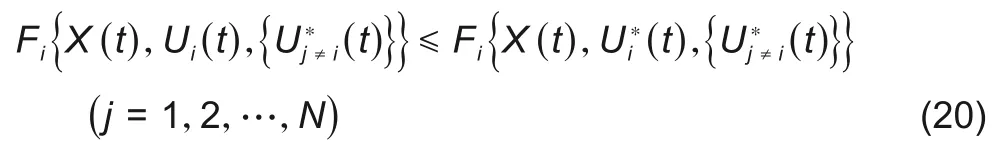
式中，X(t)=Xi(t)⋃{Xj≠i(t)}。

纳什最优决策隐含一个问题，即要达到整体系统最优，每个VPP优化自身各自子目标前需获得其他VPP子系统的最优解。本研究引入分布式结构，使得各个VPP可有效利用网络通信互传信息，为EMPC迭代求解提供条件。首先，每个VPP预先估计其t时刻对应的初始解，并将预估解发送给联合系统内所有的VPP，联合系统内每个VPP利用其他VPP的预估解来求其最优解；然后，每个VPP比较运算出的最优解和上次计算的最优解，并将计算的最优解和比较结果传送给其他VPP；如果两次迭代结果满足给定精度，则迭代结束，否则，整个联合系统未达到纳什最优条件，需进行进一步地调整。t时刻迭代结束后，进行t+1时刻求解，重复上述过程。

2.1.3 自适应域长度的确定

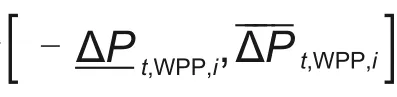
传统MPC预测域或控制域长度是固定的，对于固定的控制域或预测域，如果步长选取过大，影响系统准确性的同时增加寻优时间；步长过短，则会陷入局部最优而不能兼顾全局。为此，本研究设计了一种自适应域长度的MPC，当风电预测误差偏大时，将自适应缩短预测域长度，从而降低预测误差对于优化结果的影响，同时也能提高控制性能。另外，对于本研究的多VPP系统，为方便处理，各VPP均采用一致的预测域和控制域长度。若滚动优化初始预测域步长为Nf0，控制域与预测域长度保持一致且同步进行调整，则自适应步长调整遵循的法则为

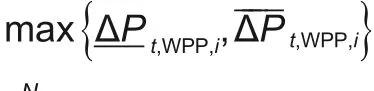
2.1.4 求解算法

本文优化调度问题涉及的约束条件及变量比较多。粒子群算法具备求解效率高、准确率有保障的特点，适合作为本文的求解算法。然而，普通粒子群算法求解时会出现收敛速度慢、可操作性低等问题。最近研究中，以量子力学为基础，提出了量子粒子群算法[14]。由于粒子具有量子行为，无法再用速度、位置等物理量来形容其状态，而是用概率密度函数Ψ(x,t)来表示其出现在某一点的概率。粒子的出现概率采用薛定谔波动方程予以描述，粒子的位置则通过蒙特卡罗方法来模拟。因此，相比普通粒子群算法，量子粒子群算法在收敛速度上具备明显的优势，本研究就选其作为求解算法。

2.2 日内实时反馈

风电预测误差不可避免，在日前滚动优化阶段每个调度间隔内使用的风电出力应用于日内阶段时一般都会发生改变，故日内调度只在各个VPP内部进行实时反馈校正，将日前滚动优化阶段的执行间隔∆T分割为等长度的m个更小时间间隔∆t。由于可中断负荷调度周期较长，故在日内反馈中将不对其优化调度。因此，日内阶段是根据日前计划结合风电更短时间尺度的预测值去调整包括燃气轮机、储能设备、VPP与大电网、VPP间联络线交互功率等在内的控制变量。当对应大间隔∆T内的m个小间隔∆t都调整完成后，就返回日前调度进入下一时域的滚动优化。

传统日内调度一般只考虑弥补与日前计划值的偏差，日内调度结果的经济性往往难以评估。为此，本文构建的日内调度策略在考虑弥补日前计划偏差的同时，还计及了经济性，即对于每个间隔∆t，优化目标为间隔内弥补日前计划值偏差同时运行费用最小，目标函数如下

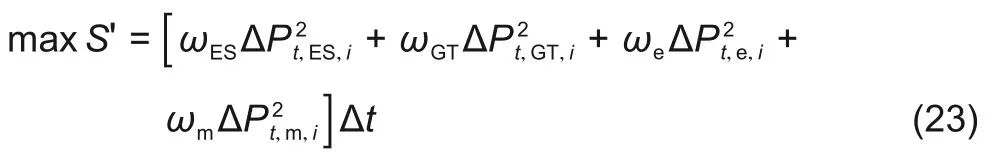
式中，ωES、ωGT、ωe、ωm分别为储能设备功率、燃气轮机功率、与大电网交互功率、与其他VPP交互功率的调整惩罚成本系数；∆Pt,ES,i、∆Pt,GT,i、∆Pt,e,i、∆Pt,m,i分别为储能设备功率、燃气轮机功率、与大电网交互功率、与其他VPP交互功率的调整值。

3 算例分析

选取某开发区能源系统作为研究算例，系统内含3个VPP参与博弈，各VPP内部结构如图3所示。其中：VPP1、VPP2和VPP3中风电容量分别为50、20和30 MW；MT采用同一型号机组，容量均为20 MW；可中断负荷最大切断量为总负荷的10%；储能设备最大充放电功率为10 MW，储能容量50 MW·h；大电网售电电价为0.4元/(kW·h)，购电电价为1.1元/(kW·h)，VPP间交易价格介于0.4～1.1元/(kW·h)之间；日前滚动优化阶段，取最大预测域长度为6 h，优化时间间隔∆T=1 h；日内实时反馈阶段，取∆t=15 min。VPP单元其他参数见表1。

图3 算例研究的能源系统结构Fig.3 Energy system structure for case study

表1 VPP各单元参数Table 1 Parameters of each unit of VPP

3.1 VPP日前协调运行结果

为说明本文优化调度方案的优越性，设置以下3种运行场景：

（1）各VPP单独优化以前获得自身最大利润；

（2）各VPP协同合作，同时参与大电网交易及VPP之间直接交易；

（3）各VPP合作，只有多VPP直接交易。

3种场景下的VPP收益见表2、图4。对比3种场景下VPP利润可知，3个VPP联合调度后，场景2、3相 较 场 景1，3个VPP总 利 润 分 别 提 高26.75%、33.24%。这是因为各VPP独立运行时，VPP内高负荷时从电网购电电价高，内部燃气轮机处于高负荷运行状态，提高了运行成本；而各VPP间可直接交易时，VPP间直接交易电价低于电网购电单价，从而提高VPP的收益。可见本文构建的多VPP联合调度模型是一种有效的利润分配方法，有利于提高VPP运行的整体经济性。

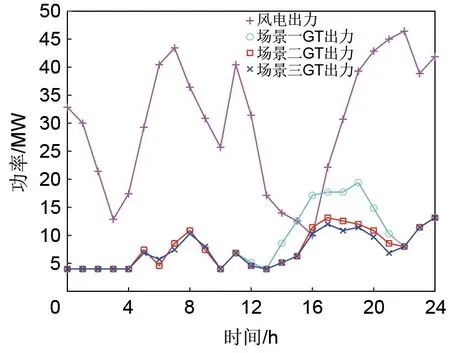
图4 3种场景下燃气轮机出力对比Fig.4 Comparison of gas turbine output in three scenarios

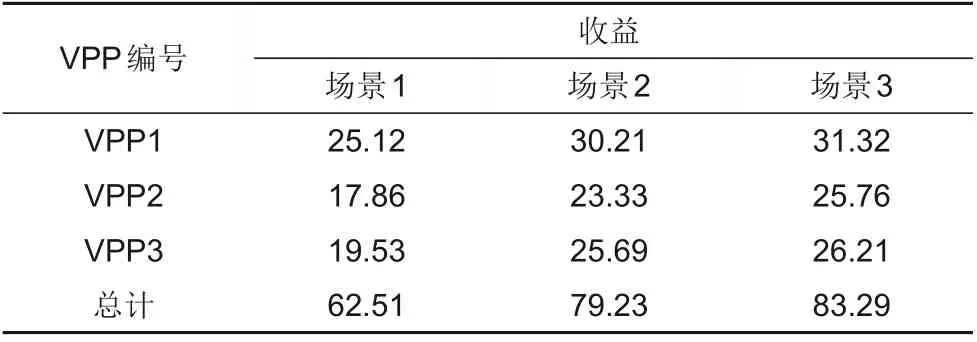
表2 3种场景下各VPP的运行利润Table 2 Operating profit of each VPP in three scenarios

图5为VPP1在场景1和场景2下的VPP与大电网及其他VPP的总交易电量。由图5可知，在11:00—15:00时段，场景2下VPP1出售更多的电量；在16:00—19:00时段，由于风电出力不足，需购买更多电量。由于VPP间直接交易电价介于大电网购售电的电价之间，场景2下交易电量明显高于场景1。在算例24 h计算周期中，场景2下相比场景1，购电量增加38.35%，售电量增加15.21%。

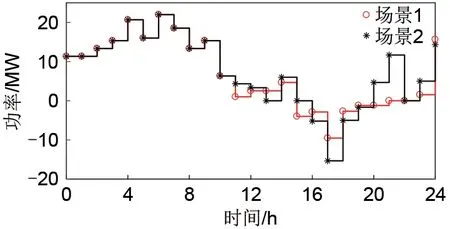
图5 场景1和场景2下VPP1交易电量Fig.5 Transaction power of VPP1 in scenario 1 and 2

场景2和场景3中3个VPP的日前交易电量如图6所示，功率大于0为出售电量，小于0表示从外部购电，在VPP中风电富余的时段，则参与电量交易。在16:00—19:00时段，VPP2风电出力较大，向外部出售大量的电量。场景3下，由于电量交易仅限于VPP间，VPP2富余的风电由其余两个VPP共同消纳，与场景2相比较，VPP1、VPP3购买电量更多。由此可见，VPP间直接进行交易，在一定程度上减小了电网的负担，多VPP联合运行，为未来构建大区域能源互联网提供了参考。

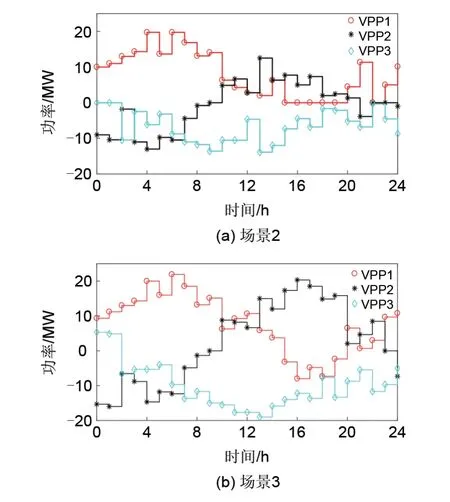
图6 场景2和场景3下各VPP交易电量Fig.6 trading capacity of VPPS in scenarios 2 and 3

3.2 日内反馈优化结果

以VPP1为例，场景2下虚拟电厂内各资源日前、日内优化结果如图7所示。可见，当仅采用日前优化结果时，由于日前风电出力预测的误差较大，负荷高峰时需要切除大量的可中断负荷来满足供需平衡，而加入日内实时反馈校正之后，由于日内实时调度精度高于日前，可切断荷量大大减小，相较日前减少66.94%，因此两阶段优化调度模型能在满足用户需求的同时提高系统运行的平稳性。

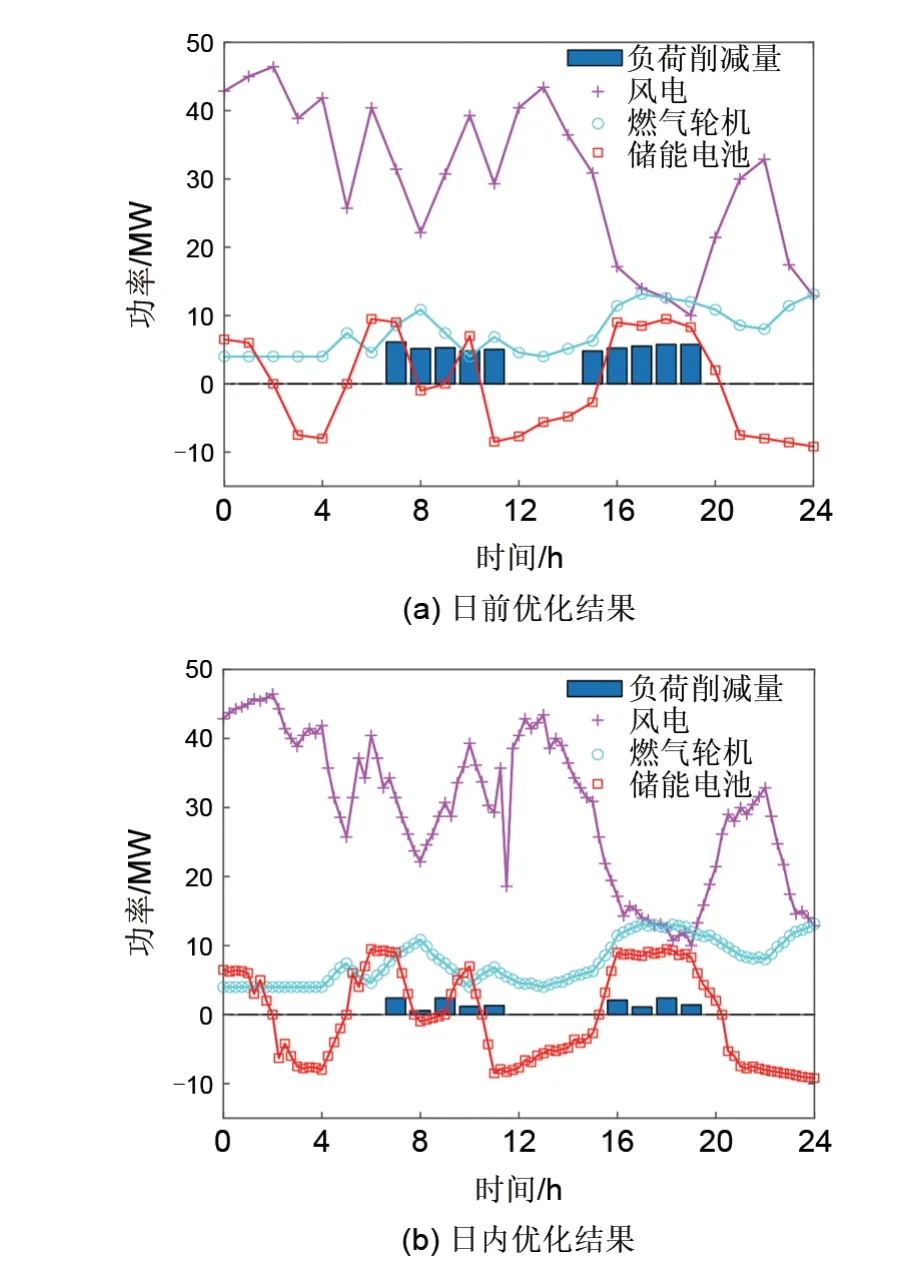
图7 VPP1日前、日内优化调度结果Fig.7 Scheduling results of day-ahead and intra-day for VPP1

3.3 自适应域长度与定长度滚动优化对比

为进一步说明自适应域长度滚动优化的优越性，将其与传统的定长度滚动优化作对比。以VPP1为例，图8为有无自适应域长度下日前调度结果与实际运行中交易电量误差(VPP1与其他VPP及大电网交易电量误差之和)对比结果，由于自适应域长度EMPC根据风电预测误差进行实时调节，各时段误差明显小于定长度滚动优化，总误差减少78.28%，因而更具有前瞻性，规避了联络线功率频繁波动问题，提高了VPP整体运行的经济性。

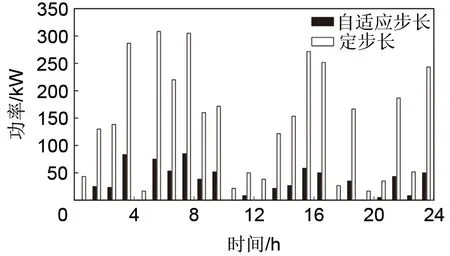
图8 有无自适应域长度下的日前联络线功率误差对比Fig.8 Comparison of power error of day-ahead tie line with or without adaptive field length

4 结 论

（1）相较于VPP单独运行，基于非合作博弈的多VPP日前协调调度模型，能够提高多VPP系统整体及各VPP自身的经济性。算例分析表明，增加VPP间直接交易后，场景2、3相较场景1，3个VPP总利润分别提高26.75%、33.24%，对于调动各VPP参与协调调度的积极性是有利的。

（2）日前日内两阶段优化调度模型精度高，很大程度上可减少可切断负荷量，相较仅仅考虑日前调度减少66.94%，提高用户舒适度的同时减少支付给用户可切断负荷的补偿成本，提高经济性。

（3）滚动优化控制域和预测域根据风电预测误差采用自适应步长后，各时段交易电量误差都有所减少，最大减少量达140 kW，总误差减少78.28%，有利于减少联络线的功率波动。