磁轴承过临界同步阻尼技术研究

刘亚婷，张 剀，徐 旸

（清华大学工程物理系，北京 100084）

飞轮储能是一种新型高效的机械储能技术，能够将电能、风能、太阳能等能源转化为飞轮的旋转动能，进而加以储存。目前飞轮储能向着高能量密度、高转速方向发展，面临着较高的技术难度，包括飞轮复合材料及结构技术、磁轴承技术等[1-4]。而旋转机械的功率密度要求不断地提高，促使转子工作转速不断提高，转子的轴承跨度增大，这些设计参数的调整使得转子的工作转速不得不超过转子弯曲临界转速，而在过临界过程中，转子自身不平衡引起的强迫振动幅度将明显增大甚至直接导致系统失稳。转子要越过临界转速工作，必须及时衰减临界转速附近的转子振动幅度，才能够实现稳定的过临界。

电磁轴承支承特性可随频率进行调整的特点使得转子的刚度与阻尼系数可控，但系统带宽等因素的限制对弯曲临界转速附近的转子动平衡提出苛刻的要求。为获得相位超前的电磁控制力，控制器参数也需要精细地调整，而控制器参数的调整受到其他振动模态、系统噪声水平等各种因素的制约，实际系统中要获得足够的电磁阻尼力，往往非常困难。

本文针对磁轴承转子越过一阶临界转速存在的问题与风险，基于同步控制思想，提出同步阻尼控制法：基于位移传感器检测到的同频位移信息，在控制回路中叠加具有特定增益与相位的正弦信号，直接生成具有超前相位的电磁力，等于为转子提供纯阻尼力，有效控制转子在弯曲临界附近的不平衡响应。

1 挠性转子不平衡

以典型Jeffcott一阶挠性转子模型为例，如图1所示，转子模型由一圆盘和无质量弹性转轴组成。转轴未变形时，圆盘中点Oꞌ与转轴中点O重合；转轴发生挠曲变形时，Oꞌ与O的距离为r。

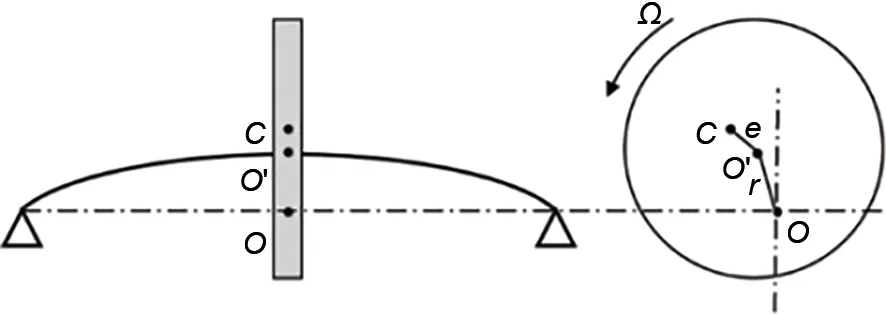
图1 存在质量偏心的Jeffcott挠性转子Fig.1 Jeffcott flexible rotor with eccentric mass

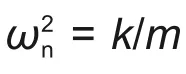
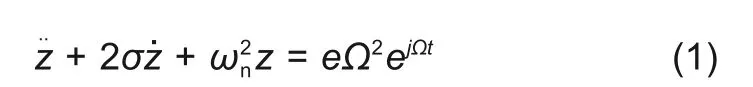
通解格式为

式中，θ为质量偏心O'C与位移偏心OO'的夹角。

不妨定义频率比λ=Ω/ωn，阻尼比ζ=σ/ωn，计算得位移偏心与质量偏心的幅值比为

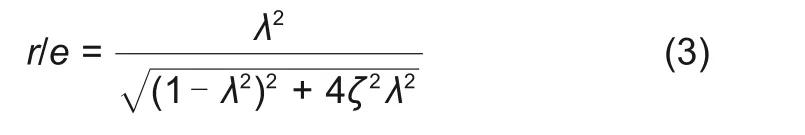
夹角满足

根据上式可知，转子在临界频率附近时，转子位移偏心OO'急剧增大，且相对偏心激励落后90°相位，即转子受到相对位移超前90°的不平衡激振力，这使得系统过临界面临失稳问题。

2 不平衡控制算法

目前转子不平衡控制研究主要针对刚性转子系统展开，通用陷波器法为一典型途径。在控制器前加入通用陷波器模块，能够使得控制器对刚性转子质量偏心引起的不平衡不作响应，帮助刚性转子在固有频率附近围绕惯性主轴稳定工作，实现力自由控制。

本文在系统中保留力自由模块的同时，加入同步阻尼控制模块，此时系统的组成框架如图2所示，其中C和P分别为控制器与转子模型，Nf模块为通用陷波器模块[5]，Nc为同步阻尼模块。

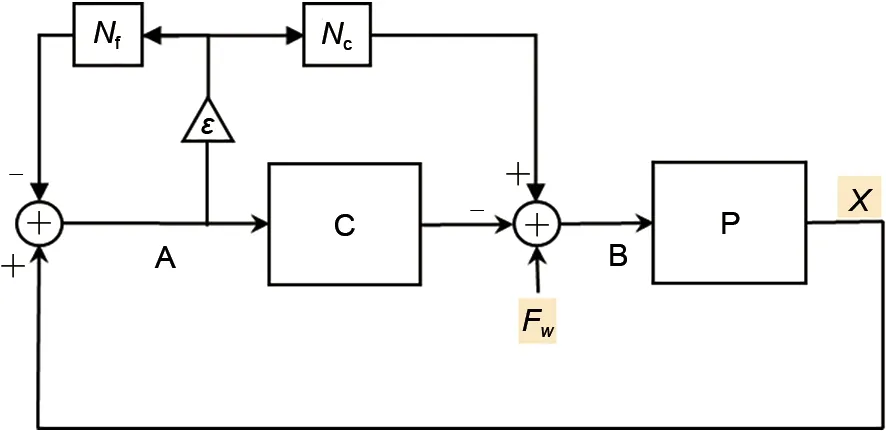
图2 含同步阻尼模块的磁轴承系统框图Fig.2 Magnetic bearing system with synchronous damping module

由图2可得不平衡激振力到转子输出位移的闭环传递函数为

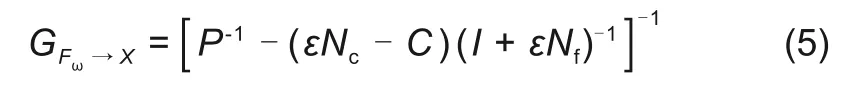
式中，ε为收敛因子。

同步阻尼模块Nc的内部结构如图3所示。

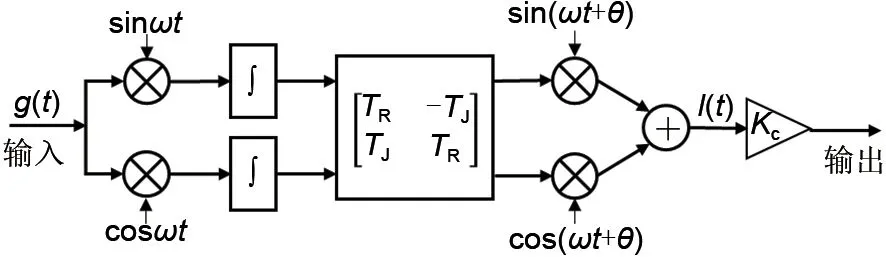
图3 同步阻尼模块内部组成结构Fig.3 Internal structure of synchronous damping module

由图可得同步阻尼模块的频域传递函数为

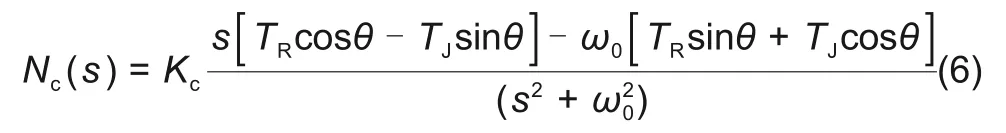
式中，θ为可修改的相位超前量，放大系数Kc将相位调整后的位移信号转换为具有超前相位的控制力，称之为同步力增益参数。

3 转子模型

研究转子系统的不平衡响应时，为了设计合适的控制器，需要良好的转子结构模型。为得到合适的简化磁轴承模型，默认传感器与功率放大器均理想。实验转子简图和部分参数如图4与表1所示。

图4 转子结构简图Fig.4 Rotor model

表1 实验磁轴承系统的部分设计参数Table 1 Part of the system design parameters

有限元法能够获取与实际转子十分接近的动力学特性，所得模型与仿真结果更为贴近和准确，但该方法难以给出阶次较低的简化系统状态方程，不便于后续控制器的设计以及仿真分析，模态分离法易获得简化转子模型。本文利用有限元分析法与模态分离分别建立了挠性转子模型。

3.1 有限元分析

目前为止，有限元方法是获取挠性转子模型的适用范围最广的方法，已有比较成熟的商业软件。在ANSYS中建立图4所对应的挠性转子模型，保留转子前端与后端的x、y共4个状态变量进行降阶，假定转子是轴对称，获取挠性转子的传递矩阵A、B、C、D的参数。

基于传递矩阵的波特图测量转子的临界转速信息，取单一方向为例，如图5所示，测量得降阶后转子模型有2个刚性模态与2个挠性模态，其中一阶挠性临界频率为829 Hz。

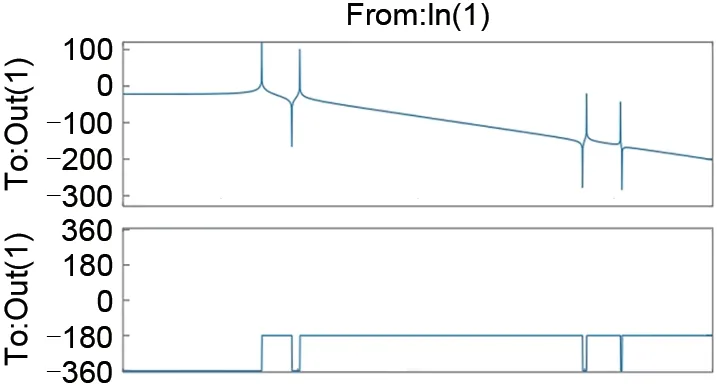
图5 有限元模型的单向波特图Fig.5 Single-direction Bode plot of the finite element model

3.2 模态分离法

已知，磁轴承转子的动力学方程

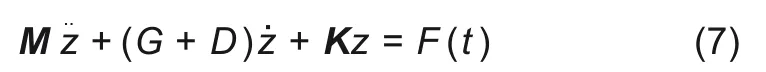
式中，质量矩阵M实对称，即M=MT>0；刚度矩阵对称，满足K=KT>0。这里不考虑陀螺效应与转子本身阻尼，即假定G=D=0。

式(7)的特征值方程为

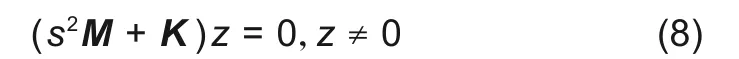
对转子上n个节点进行分析，即有4n个自由度。式(8)的解为一组固有频率ωi和与之对应的振型φi(其中i=1,2,…,4n)。特征模态与质量阵和刚度阵均具有正交性，因此缩放特征模态能够在质量矩阵归一化的同时将刚度矩阵对角化

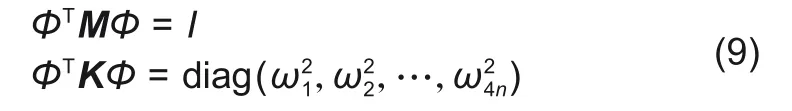
此时式(8)的解为特征模态的线性组合

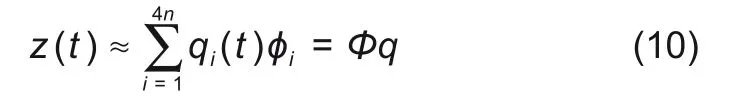
式中，qi为模态幅值。因此可转换式(7)为

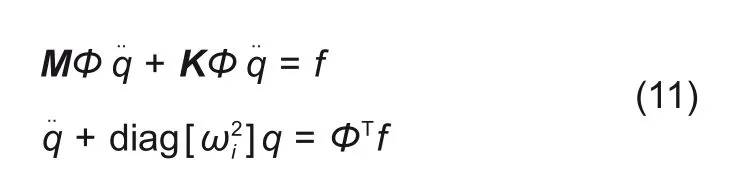
其中i=1,2,…,4n，那么电磁力与转子位移的关系为

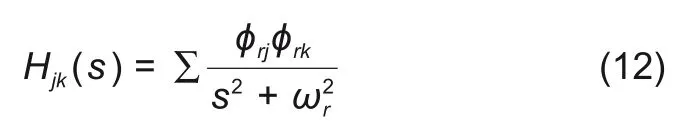
由式(12)可见转子临界转速、振型和支承刚度变化的影响等动力特性的获取十分重要。数值方法随着计算机技术的发展越来越受到重视，质量离散法为其中一种，能够高效地近似计算临界转速。本课题利用质量离散化与模态分离法建立转子在一阶弯曲临界的传递函数模型，并依据传递矩阵得电磁力到位移测量点的单向波特图如图6所示，转子振型如图7所示，由振型图可知所得转子模型含2刚性模态与2挠性模态，测量可得转子一阶弯曲临界频率为909 Hz。与有限元模型相比较，在可接受的误差范围内。

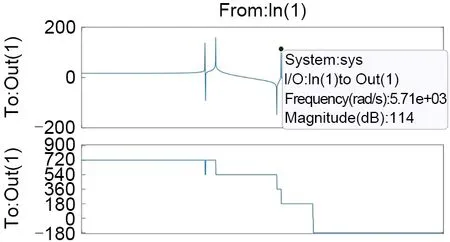
图6 模态分离所得转子模型的单向波特图Fig.6 Single-direction Bode plot obtained from modal separation

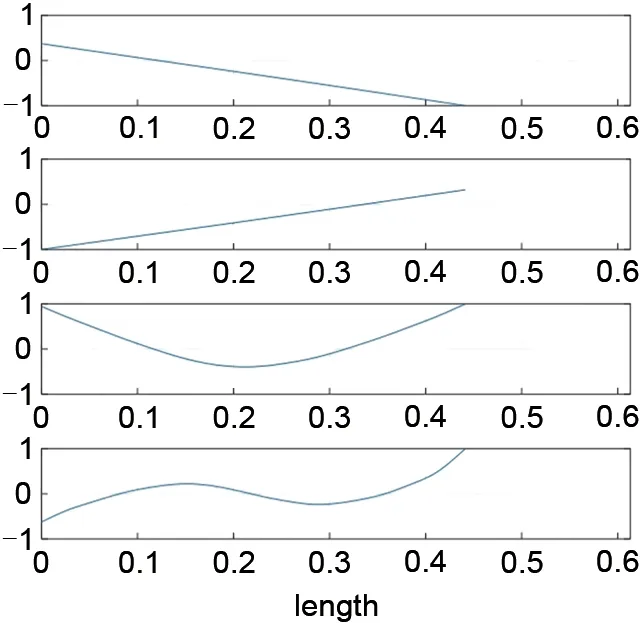
图7 挠性转子的振型图Fig.7 Vibration shape of flexible rotor

在一阶弯曲临界转速附近，转子动力学模型中可近似忽略刚性转子模态以及更高阶次的弯曲模态，直接简化为仅含有一阶挠性模态的传递函数。

由转子模型计算得包含力电流参数在内的转子传递函数

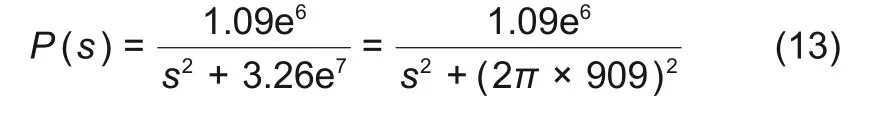
4 挠性转子不平衡仿真

4.1 有限元模型仿真

本节针对有限元方法建立的挠性转子模型，在Simulink环境下搭建仅含有控制器与转子模型的原始系统模型，如图8所示。

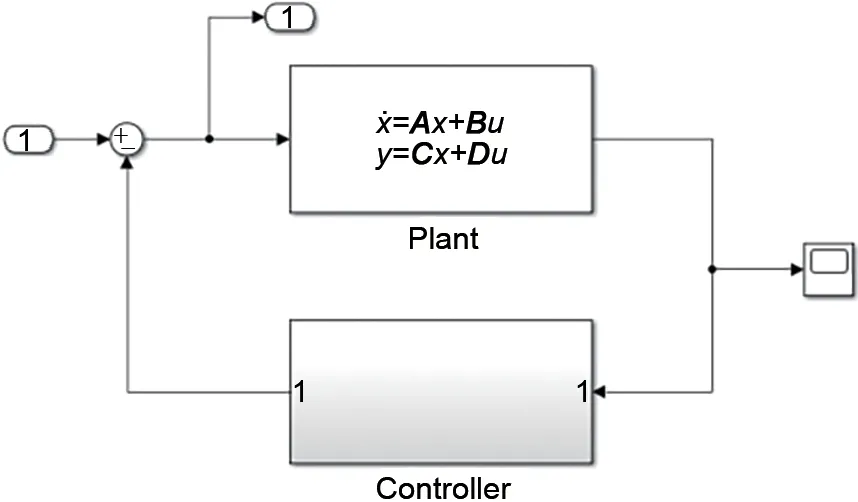
图8 挠性转子系统原始模型Fig.8 The original system

设置系统工作在一阶挠性频率(827.9 Hz)附近。系统中仅加入控制器的情况下，转子的运动轨迹如图9所示，四个颜色分别代表转子左右两节点x、y方向上4个自由度。此时，控制器能够为转子提供一定的阻尼，转子能够在临界转速稳定，但代价是控制器高频增益较高，实际工程实现时系统稳定裕量会明显削弱。

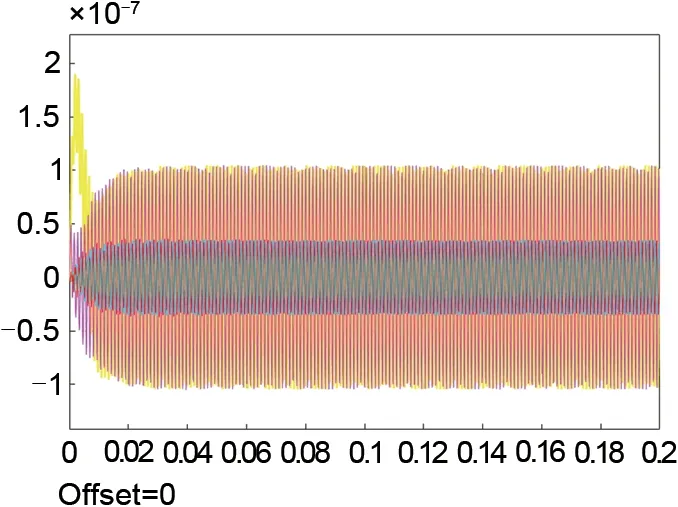
图9 仅含控制器时的转子运动轨迹Fig.9 Rotor motion trajectory with controller

在控制器前加入通用陷波器模块，收敛因子为10时，转子轨迹如图10所示。通用陷波器去除了位移信号中的转速同频成分，控制器对同频干扰无反应，而此时具有超前相位的不平衡激振力将促使转子振幅不断增大，系统失稳。故在刚性转子系统中表现良好的力自由控制法不能简单应用于挠性转子系统。

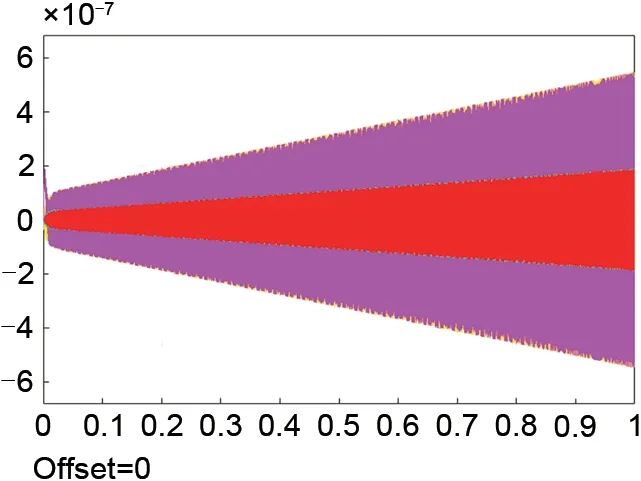
图10 加入通用陷波器Fig.10 With the general notch filter

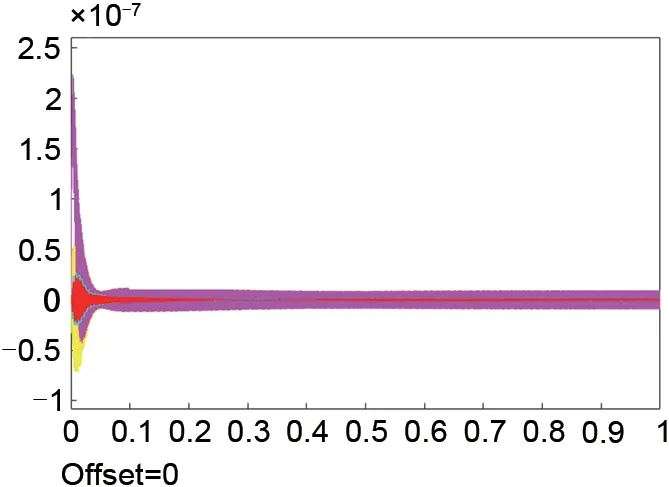
图11 加入同步阻尼模块Fig.11 With the synchronization damping module

向含力自由模块的系统中加入同步阻尼模块，设置收敛因子为1，超前相位90°，同步力增益Kc=1e8，在转速接近弯曲临界时，转子的运动轨迹如图12所示。由图可知，转子在临界附近的振动迅速衰减，验证了同步阻尼模块应用于挠性转子一阶弯曲临界的可行性。接下来探讨同步阻尼模块参数对系统性能的影响。

4.1.1 同步力增益参数

固定收敛因子ε=10，超前相位θ=-π⁄2，修改同步力增益参数取值，仿真得转子单自由度位移如图12所示。由图12(a)～(c)可知，随着Kc取值的增大，转子振动幅度的衰减越来越快，且稳定后振动幅度逐步减小；但该同步力增益存在一个上阈值，如图12(d)所示，Kc取值过大时，系统将迅速失稳。

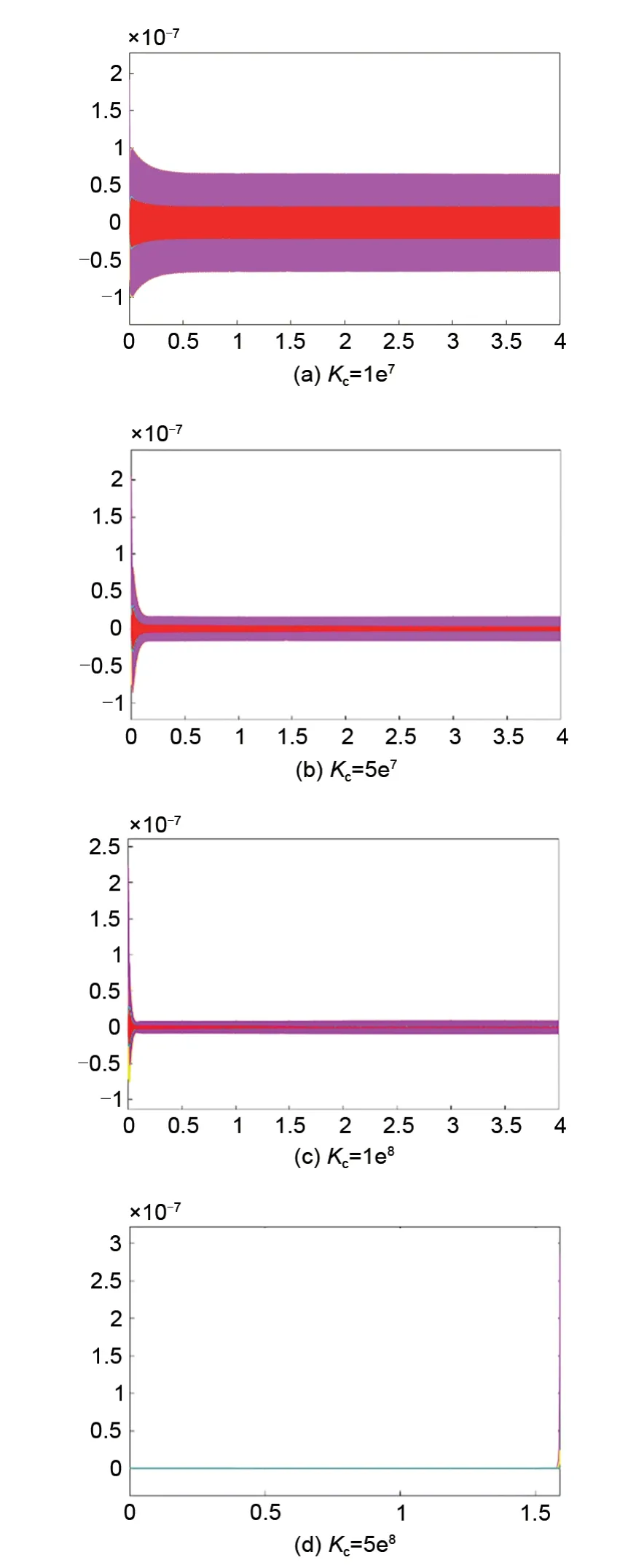
图12 不同同步力增益下的转子运动轨迹Fig.12 Rotor trajectory with different Kc

4.1.2 超前相位

设置收敛因子ε=10，同步力增益放大参数Kc=1e8，修改超前相位θ的取值，测量转子输出位移如图13所示。

由图13可知，采用同步阻尼方式对临界转子进行控制时，超前相位存在一个稳定的工作范围，当超前相位远离-90°时，转子位移振动衰减时间变长。

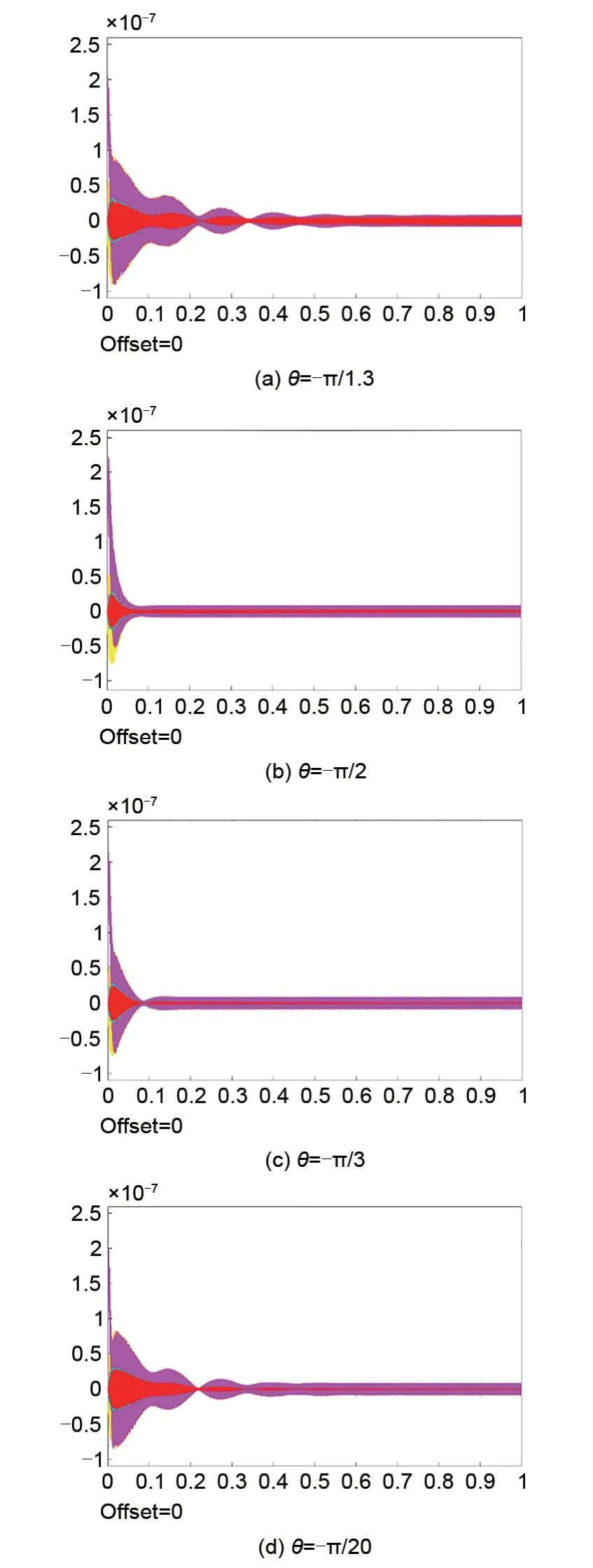
图13 不同相位超前值对应的转子运动轨迹Fig.13 Rotor trajectory with differentθ

4.2 模态分离模型仿真

为简化后续理论验证工作，控制器仅取PID的比例环节。不妨简化控制器的传递函数C(s)=1。力自由环节与同步阻尼模块的获得矩阵T直接取单位阵，故不平衡干扰力Fω到转子输出位移X的闭环传递函数为

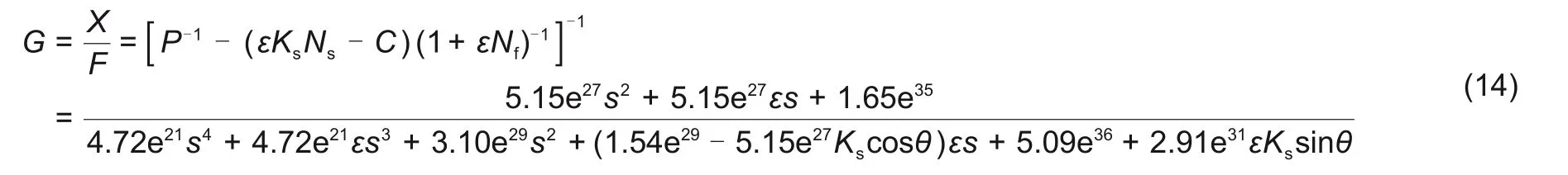
式中，ε为收敛因子，Kc与θ分别为同步阻尼模块的力增益参数与超前相位。接下来在极点计算的同时，在Simulink中搭建对应参数的磁轴承模型进行仿真对比。

在转子输入端额外叠加超前90°，幅度为1的900 Hz噪声。当系统中含有通用陷波器，即力自由模块时，取收敛因子为1时，极点虽然均位于左半平面，但收敛速度极慢，且虚部对应的数值与转子临界转速十分接近，依然不能够满足实际工作需求，对应转子运动轨迹如图14所示。

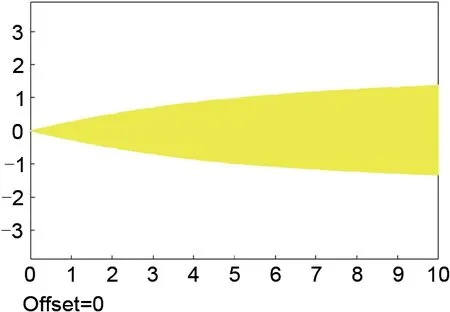
图14 加入通用陷波器对应的转子运动轨迹Fig.14 Rotor trajectory with the general notch filter

接下来，向转子系统中加入临界阻尼控制环节，不妨取力自由控制模块的收敛系数ε=10，同步阻尼控制模块的超前相位为90°，同步力增益Kc=500，此时噪声干扰下的转子位移如图15所示。由图可知，在转子模型中本身不含阻尼且控制器未提供阻尼的情况下，转子运动轨迹是收敛的，可见同步阻尼控制能够帮助转子越过一阶临界转速，提高磁轴承系统的工作转速。

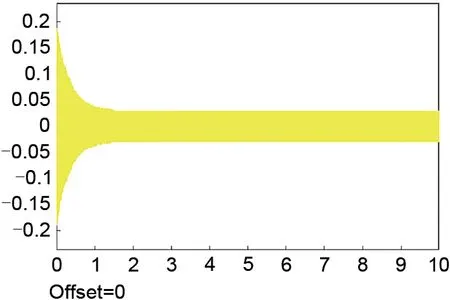
图15 加入同步阻尼模块对应的转子运动轨迹Fig.15 Rotor trajectory with the synchronization damping module

由式(14)可知，收敛因子ε和同步阻尼模块的Kc与θ的取值对系统的工作状态均有影响，接下来分别进行讨论。

4.2.1 收敛因子

固定同步阻尼环节的超前相位为90°，同步力增益参数Kc=1000。改变ε的取值，分别计算干扰力到转子位移的传递函数极点，结果如表2所示。

表2 Kc=1000，θ=-90°时系统闭环传递函数的极点随ε的变化Table 2 the poles of the closed-loop transfer function with differentεwhen Kc=1000,θ=-90°

根据计算结果，转子的振动衰减速度随着收敛因子的增大而变快，但ε存在稳定的上阈值，取值过大时，转子系统将失稳。在Simulink中修改力自由模块的收敛因子与上述计算一致，并分别进行仿真，转子系统的输出位移如图16所示。

仿真可得当极点均位于左半平面时，转子的运动轨迹也是收敛的。且由图16(a)～(c)可得：系统稳定的前提下，随着收敛因子的增大，转子振动幅度收敛速度不断增快，且稳定后的转子运动幅度随之减小。当收敛因子过大，如图16(d)所示，转子的运动轨迹向外发散，系统失稳，与极点分布相一致。

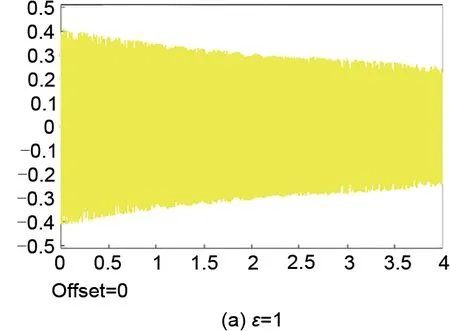
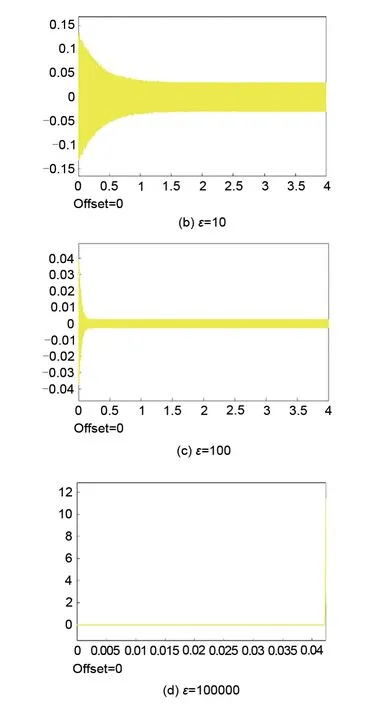
图16 不同收敛因子下转子运动轨迹Fig.16 Rotor trajectory with differentε

4.2.2 同步力增益参数

固定收敛因子ε为10，相位超前-90°，修改同步力增益参数Kc，得到系统传递函数的极点如表3所示。

表3 ε=10，θ=-90°时系统闭环传递函数的极点随Kc的变动Table 3 the poles of the closed-loop transfer function with different Kc whenε=10,θ=-90°

对比多组计算结果可知，当同步力增益Kc取值过大时，传递函数将存在位于右半平面的极点，系统是不稳定的，而在系统稳定的前提下，Kc越大，转子的振动衰减越快。

仿真得表3中前四组参数下转子系统的单向输出位移如图17所示。

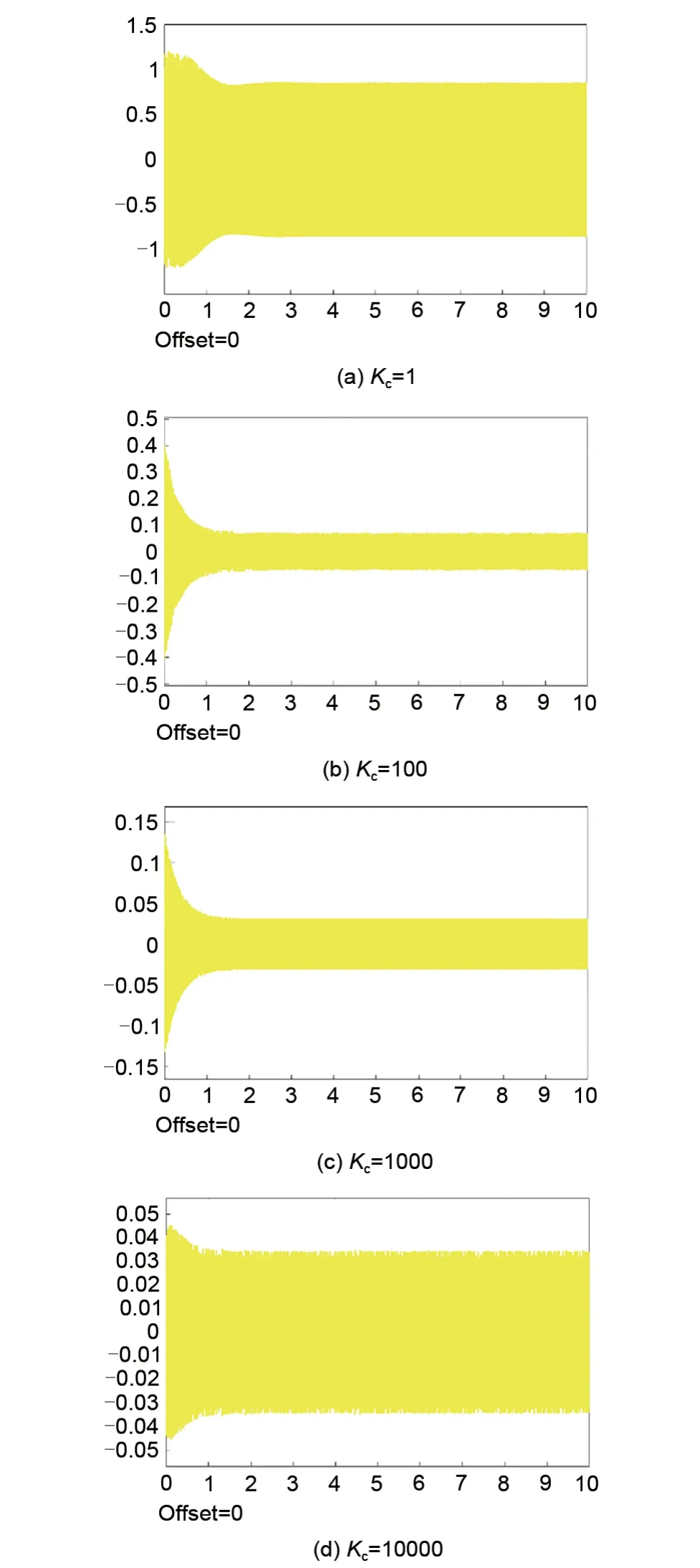
图17 不同同步力增益参数下转子的位移轨迹Fig.17 Rotor trajectory with different Kc

当同步力增益Kc取值为100000及以上时，仿真结果显示系统直接失稳，故该参数也存在一个稳定上限。对比图17可得，同步力增益参数Kc的值越大，转子的运动轨迹收敛越快，稳定后转子位移幅度越小。

4.2.3 超前相位

固定收敛因子ε=100，同步力增益参数Kc=100，修改超前相位取值，计算对应的传递函数极点如表4所示。

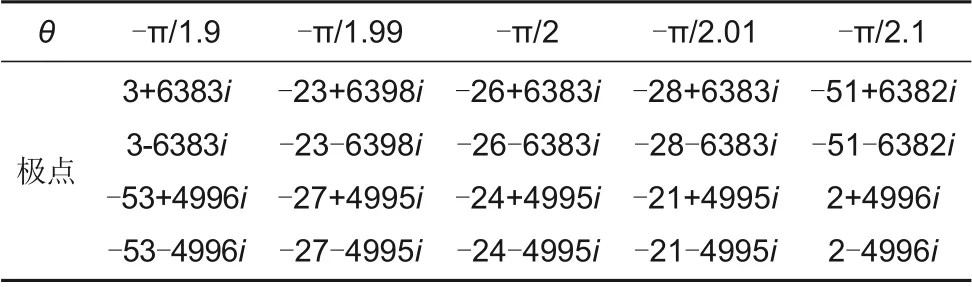
表4 ε=100，Kc=100时系统闭环传递函数的极点随θ的变动Table 4 the poles of the closed-loop transfer function with differentθwhenε=100,Kc=100

在Simulink中对超前相位进行同样的取值并分别进行仿真，得图18。

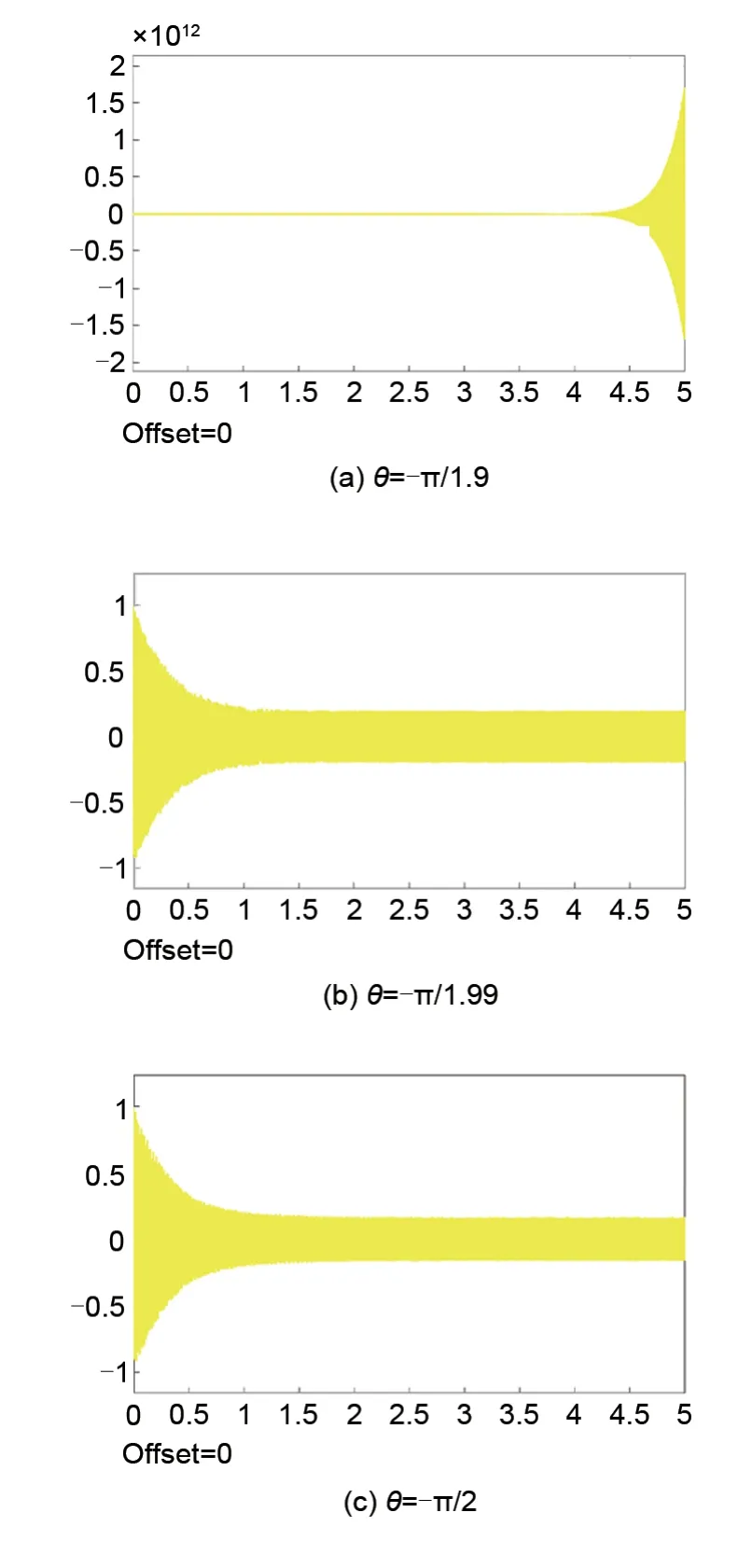
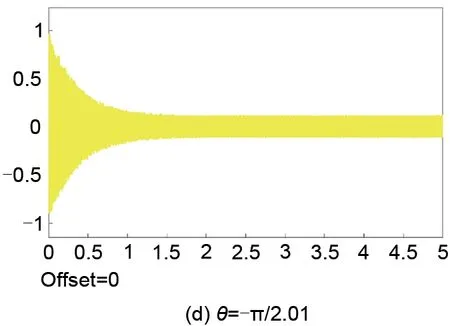
图18 不同相位偏移下，临界转速附近的转子运动轨迹Fig.18 Rotor trajectory with differentθ

对比表4与图18可知，转子系统过临界时，超前相位值为-90°表现最好，且在当前的工作参数下，为了系统稳定，θ的稳定取值范围极小。

仿真中发现收敛因子、同步力增益参数与系统相位裕度的大小相互影响。接下来分别修改收敛因子与同步增益参数的值，仿真可得-90°总是在系统稳定的超前相位的取值范围内，但是稳定范围并不以-90°为中心点，因此取超前相位稳定最大值与最小值与-90°分别作差，取其中较小值与收敛因子和同步增益参数的关系得图19。

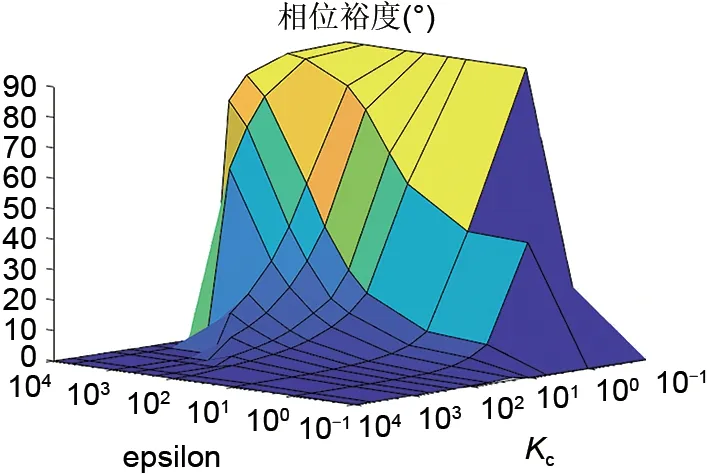
图19 相位裕度与收敛因子和同步增益参数的关系Fig.19 The relationship between phase margin and εand Kc

由图可得，相位裕度随着收敛因子ε的增大而增大，随着同步增益系数Kc的增大而减小。由于系统部件延迟、未建模因素的存在等，θ本身存在不确定度，因而实际设计参数时，应该保证系统稳定性对θ取值不要过于敏感。

4.3 仿真总结

由上述仿真可得，收敛因子、同步力增益参数和超前相位值的取值对系统稳定性均有影响，且这三个参数的取值范围是互相影响的，因此使用同步阻尼法时，需要综合考虑进行参数选取。建议固定超前相位为-90°并保留一定的相位裕度；在满足系统稳定性与实际系统所能够提供的性能要求下，适当放大收敛因子与同步力增益参数的数值，获取更迅速更稳定的抑振效果。具体取值可提前参考闭环传递函数的极点分布。

5 实验验证

实验室的电磁轴承实验平台由控制电路板、电磁轴承、保护轴承、电动主轴、电涡流传感器、光电传感器(获取键相信号)、十路单向功率放大器及测控计算机组成，实验平台及其框图如图20和21所示。

图20 实验平台Fig.20 Test platform

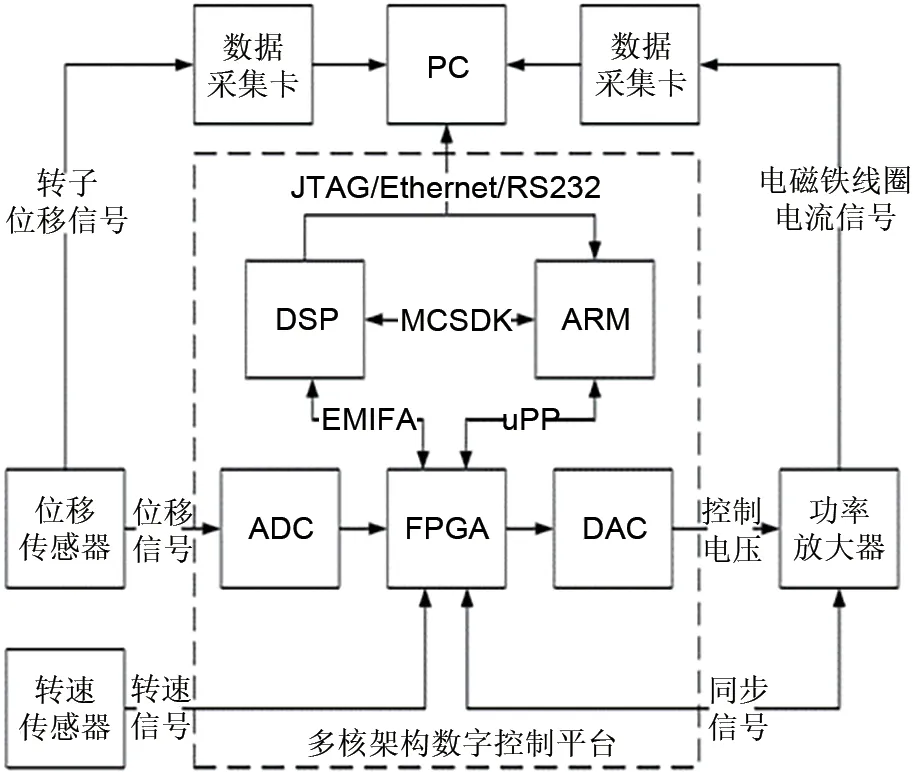
图21 实验平台框图Fig.21 Block diagram of test platform

由于已有的控制系统支持复杂的控制算法，所以在未加入同步阻尼控制模块的情况下，利用电磁轴承的加重动平衡与支承系统尽可能地为转子系统提供越临界所需的阻尼，当转子加速至弯曲频率附近时，对其运动轨迹进行观测得图22，图中上侧左两个图分别为转子上下轴心的轨迹，单位为μm，左下方为转子径向位移信号峰值，单位为V。

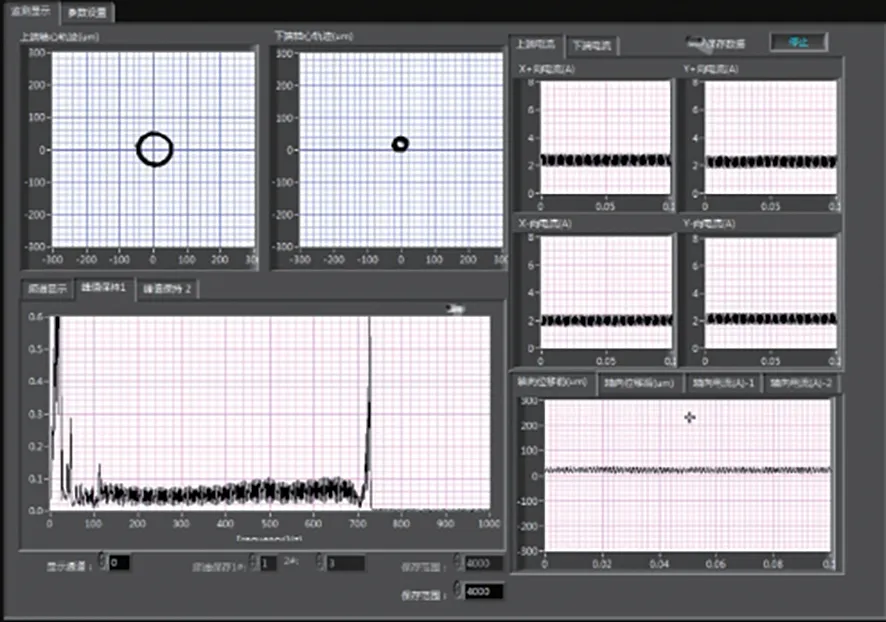
图22 转速接近临界频率，即将失稳Fig.22 Speed close to the critical frequency

由图22可知，当转子转速接近一阶弯曲临界时，转子的径向位移信号峰值接近0.6 V(本实验平台的传感器增益为59 mV/µm)，即径向位移峰值约为10µm；虽然此时转子上下两端的径向位移轨迹幅度并未超过转子的径向保护气隙，但考虑到转子同步振动随转速上升趋势陡峭，继续给转子加速存在风险。

在此基础上尝试继续加速，可得转子运动轨迹如图23所示，由于转子阻尼不足，无法及时衰减振动，转子径向轴心轨迹已经发散，与图22对比可知，转子上下两端的径向位移在增大，转子已经开始失稳。如图24所示，继续加速时转子的运动轨迹杂乱无章，且上下轴端的径向位移均已超过了100µm的径向保护气隙，转子完全跌落。

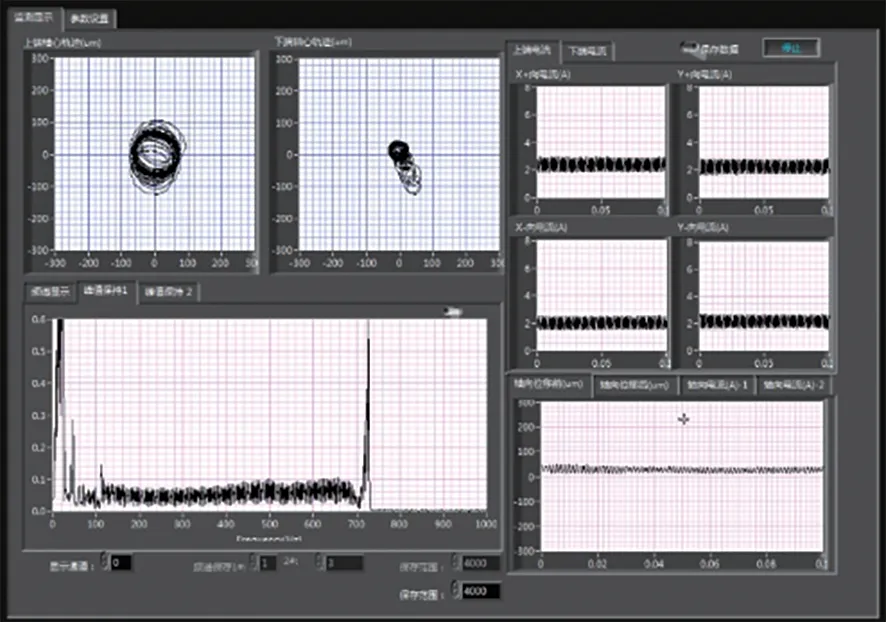
图23 转子失稳瞬间Fig.23 The moment of rotor losing stability

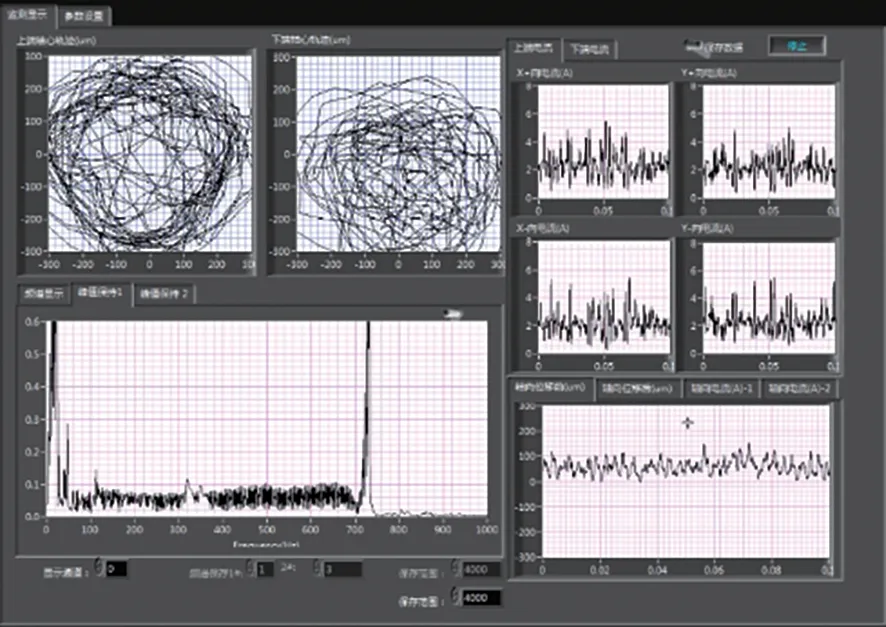
图24 转子系统彻底失稳Fig.24 Complete instability of the rotor system

不改变各环节参数的选取，即在同样的工况下，向磁轴承控制系统中加入同步阻尼控制模块。当转子加速至一阶弯曲临界转速附近时，如图25所示，对比图22，转子径向位移幅值明显降至0.4 V以下，且上下轴端的径向位移幅值均不超过40µm，表明该实验平台此时仍然能够安全运行。

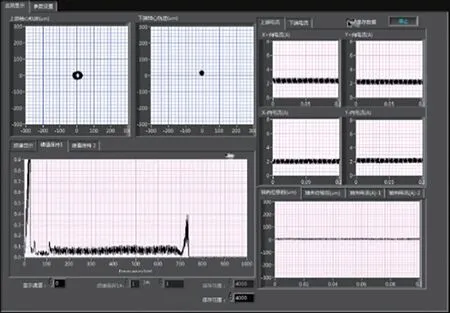
图25 转子过临界Fig.25 The rotor crossing the critical speed

此时继续给转子加速，如图26所示，在临界转速附近，转子的径向位移幅值峰值仍略小于0.4 V。而转子转速超过一阶挠性临界转速后，转子的运动轨迹能够较快地得到收敛，且转子上下轴心的运动轨迹也较稳定，幅值均不超过40µm。因此可以获得结论：同步阻尼模块能够为过临界转子提供所需要的阻尼，帮助磁轴承系统平稳地越过一阶挠性临界，达到更高的工作转速。

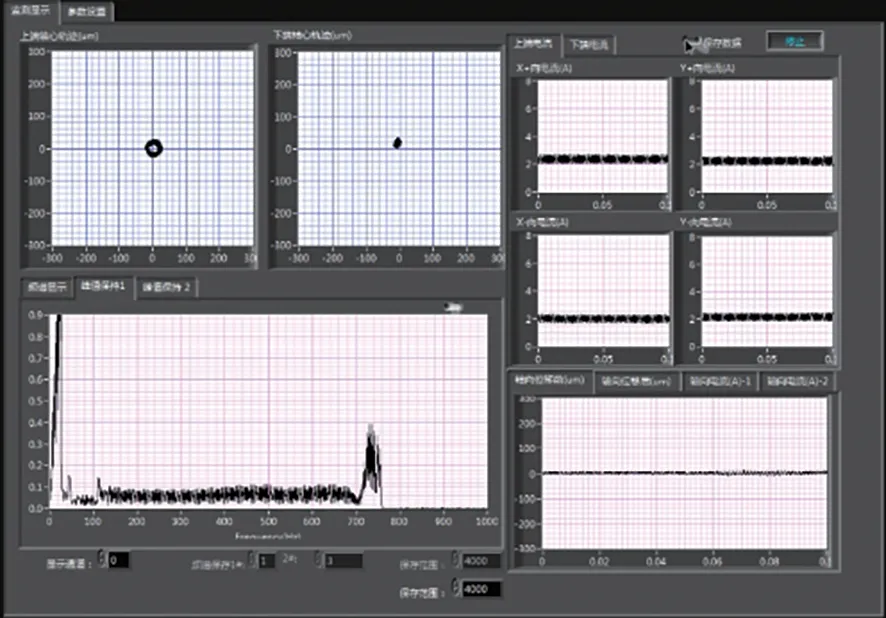
图26 平稳过临界Fig.26 Transiting the bending speed steadily

根据上述结果，不难得出结论：仅依靠电磁支承为挠性转子提供阻尼时，为了让转子平稳地穿越一阶弯曲临界，系统对控制器算法要求较为苛刻，实现难度较高。而本课题所提出的临界同步阻尼方法，能够有效抑制转子在穿越一阶弯曲临界转速时的振动，降低控制器设计难度。

6 结 论

本文针对转子跨越一阶临界转速时，临界振动抑制困难的问题，提出同步阻尼方法，并在转子有限元模型与模态分离模型中验证了此方法的可行性。首先通过仿真，分析了相位偏移与同步力增益参数的取值对系统的收敛速度和稳定性的影响。接着基于质量离散化获取转子在一阶弯曲临界附近的简化模型，在理论上验证了转子临界同步阻尼技术的可行性并对收敛因子、同步力增益系数及超前相位的取值与系统稳定性的关系进行了分析，并给出此方法的应用指导。最后在实验室已有的磁轴承系统上完成部分实验，转子稳定地越过45000 r/min的一阶弯曲临界，验证了临界阻尼控制算法的效果。