基于换热面积连续调节的单罐熔盐储热系统释热功率稳定性研究

陈晓彤 ，鹿院卫 ，何聪 ，宋文兵 ，吴玉庭 ，杨桂春

（1北京工业大学传热强化与过程节能教育部重点实验室暨传热与能源利用北京市重点实验室，北京 100124；2中国寰球工程有限公司，北京 100012）

2020年，能源消耗总量约49.7亿吨标准煤，能源问题成为当今社会的热点。可再生能源具有清洁、可持续利用的优点，但其供应却不稳定。储热技术能够将风能、光能以及低谷电以热能的形式储存起来，用于建筑供暖和工业用电，是解决能源供给时间与空间不匹配的有效方式[1-3]。双罐熔盐储热已成功应用于大型建筑供暖和太阳能发电[4-5]，它采用两个储热罐和熔盐泵，系统庞大，不适用于小型场所供暖。研究表明，采用单罐储热技术取消第二个储热罐可降低35%的成本[6]，且系统较为简单，更适合小型场所供暖。此外，国家发改委在多地实施了以电代煤的政策[7-8]，并计划于2021年实现70%的农村清洁供热，单罐熔盐储热技术也成为解决这一问题的有效途径。

诸多学者对单罐释热效果进行了研究分析。Vaivudh等[9]采用数值模拟的方法对储热罐的释热效率进行了分析，结果表明，选用不同类型的换热器会对释热效率产生较大影响，当使用螺旋管换热器时，换热效率高于垂直管换热器。崔锡民[10]与Li等[11]分别使用实验和模拟的方法研究了盘管换热器布置在蓄热罐不同高度时对释热的影响，结果表明，无论换热器如何布置，其出口温度均随释热的进行而降低，无法保持稳定。施素丽[12]利用数值计算方法研究了空气流量对释热功率的影响。当释热功率降低时，通过增大空气的流量使释热功率稳定在一定范围内。但在实际应用中，由于空气的流量过大、压力过高、阻力能耗过高。以上研究均局限于采用固定式换热器，导致释热功率无法稳定。

张银和[13]设计了三个面积递增的盘管换热器，释热初期使用换热面积最小的换热器，随着换热进行，熔盐温度降低，换热量减少；当取热水温度过低时，便启用换热面积更大的换热器。虽然增大换热面积能在短时间内显著提高换热器出口水温，但其温度仍随释热时间延长难以稳定调节。因此，本文提出一种换热面积能够连续调节的单罐熔盐系统，在不改变取热介质流量的条件下，换热器的工作面积随熔盐温度的变化而改变，以实现换热器出口温度与释热功率的稳定。

1 实验系统与原理

1.1 单罐熔盐系统

为了探究通过改变换热面积来实现释热功率稳定的可行性，本系统在实验室原有储热罐的基础上搭建了一个小型单罐熔盐储热系统，其物理模型如图1所示。蓄热罐外径Do=400 mm，内径Di=150 mm，高H=170 mm，罐壁采用316 L不锈钢，四周壁厚为5 mm，底面厚度Hbottom=50 mm，蓄热罐内外壁间填充有115 mm厚的硅酸铝保温棉以减少罐壁的热损失。蓄热罐装有5.75 kg二元硝酸盐。熔盐的具体参数如表1所示[14]。

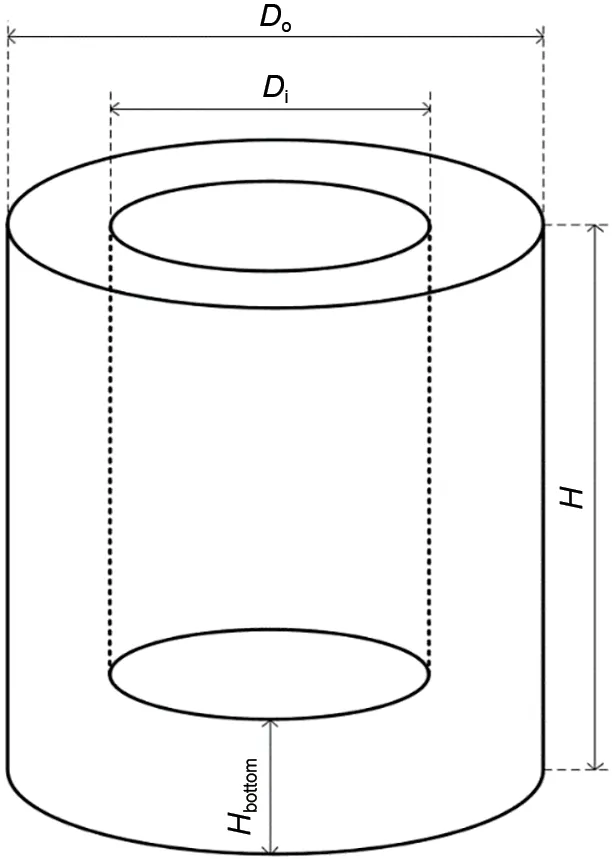
图1 储热罐物理模型Fig.1 Physical model of heat storage tank

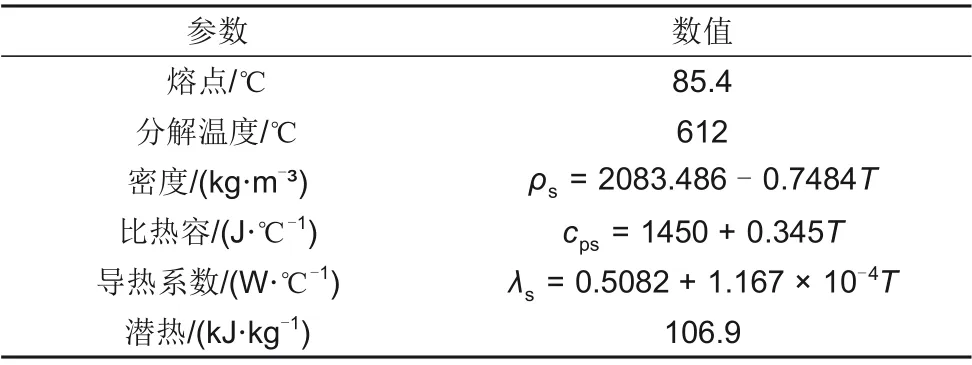
表1 二元硝酸盐的物性参数Table 1 Physical parameters of molten salt

储热时，单罐内的熔盐被电加热器加热，释热时，取热介质流过盘管换热器从熔盐侧取热。盘管换热器的管径d=12 mm，高h=180 mm，螺旋半径r=85 mm，螺距p=30 mm，释热开始前，盘管换热器全部位于熔盐液面上方。

1.2 实验原理

在单罐储热系统释热过程中，熔盐储存的热量被取热介质取出，熔盐温度不断降低，而释热功率往往随着熔盐温度的降低而减小，为了实现释热功率的稳定，当熔盐温度降低时，换热器浸入熔盐中的深度不断增加，换热面积增加。最终，换热面积的增大弥补了熔盐温度降低导致的换热量减少，释热功率得以稳定。本实验中，空气被作为取热介质，环境温度为10℃，流量为40 L/min，目标温度为200℃。

图2为本实验系统的结构示意图，换热器与丝杆升降机连接，丝杆升降机在步进电机带动下上下移动，从而改变换热器浸入熔盐中的深度。对于本系统，为了便于换热器的上下移动，因此在蓄热罐顶部未布置顶盖，并在罐体上方加装了一支架用来放置步进电机和丝杆升降机。

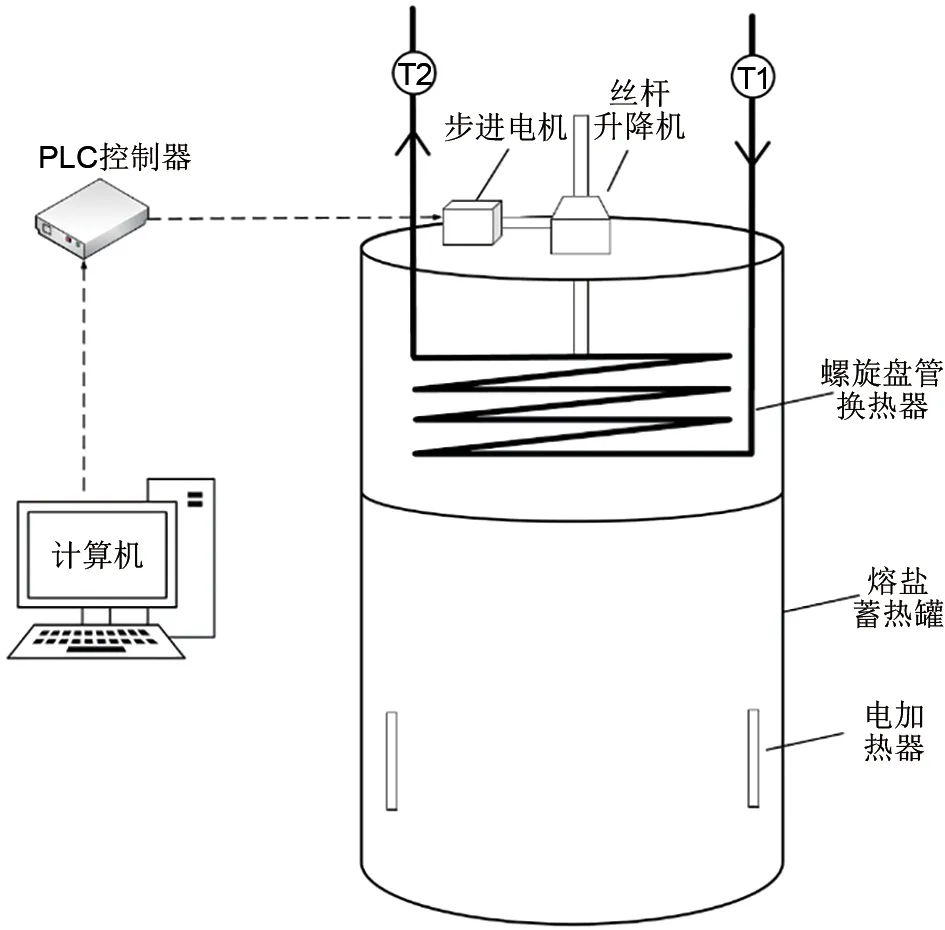
图2 换热面积调节系统物理模型Fig.2 Physical model of heat exchange area regulation system

换热器浸入熔盐中的面积可以由式(1)～(3)计算

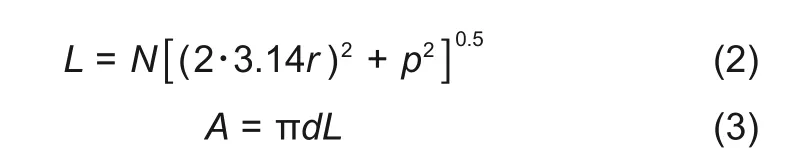
因此换热器浸没深度的改变即实现了换热面积的变化。

1.3 换热面积调节方法

为了实现换热面积的变化，本文将通过PID控制对换热面积进行调节。PID控制是一种成熟的控制方法，已成功地应用于各个行业，对于本系统，其原理是根据换热器出口取热介质的实际温度与设定目标温度之间的偏差来调整换热面积，使实际温度不断向目标温度靠近。在本系统中，通过PLC控制器向步进电机发送脉冲信号使步进电机带动换热器上下移动，实现换热面积的调节。连续PID控制的微分表达式可表示为下式

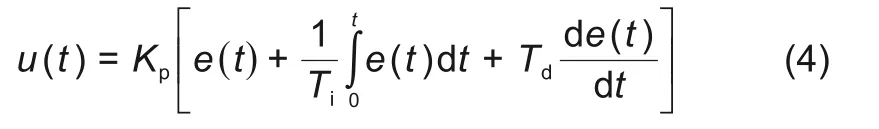
式中，u(t)为PID控制器输出的控制量，即换热器上下移动的距离；e(t)为偏差信号，即本实验中所设定的目标温度(200℃)与换热器出口的实际温度的差值；Kp为比例系数，其能够加快系统的响应速度，减小系统稳态误差；Ti为积分时间常数，能够提高控制精度；Td为微分时间常数，反映误差信号的变化趋势，并可以在误差信号变得太大之前，引入修正信号，从而提高控制系统的作用速度，缩短调节时间。因此确定Kp、Ti、Td三个控制参数即可对换热面积进行调节，而采用不同PID整定方法时，Kp、Ti、Td会有所不同，从而导致换热器移动的幅度和频率会有所不同，对释热过程产生影响，因此本文采用C-c法、Lopze法、Mcp法和Z-N法四种不同的PID整定方法进行了实验，四种整定方法的整定公式如表2所示。

表2 不同整定方法的整定公式Table 2 Setting formulas of different setting methods

在使用整定公式时，会出现K、τ、T1三个特征参数，它们分别代表增益、延迟和时间常数。对于本系统而言，增益表示换热器浸没前后出口温差与浸没深度的比值；延迟表示换热器浸没入熔盐后，出口温度快速升高所需要的时间；时间常数表示出口温度达到0.632倍的进出口温度之差时温度所需的时间，因此则需要获得换热器开始浸没至停止浸没时出口温度的变化曲线来获取K、τ、T1这3个特征参数，从而计算出控制参数(Kp、Ti、Td)进而对换热面积进行调节。

图3为换热器完全浸没时出口温度的变化曲线，对于PID控制而言，换热器开始下降的瞬间即视为下降完成，因此由图中可以得到特征参数K=1.93、τ=12、T1=65.5，通过将特征参数带入不同整定方法中进行计算，得到4种整定方法的控制参数如表3所示。

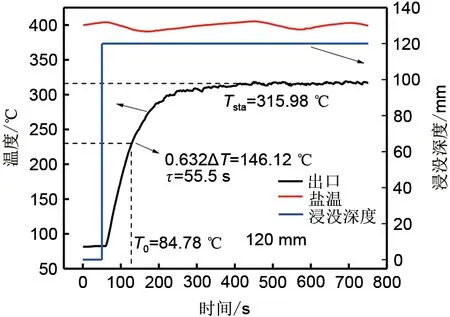
图3 换热器完全浸没时出口温度的变化曲线Fig.3 change curve of outlet temperature when the heat exchanger is completely immersed

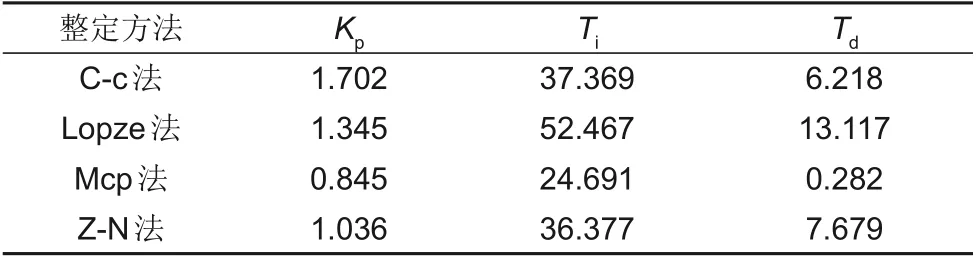
表3 不同整定方法的控制参数Table 3 Control parameters of different setting methods

将不同方法下的控制参数带入式(4)中即可获得换热器的移动量，实现换热面积的调节。

2 结果与讨论

2.1 释热过程稳定性分析

使用C-c整定方法进行面积调节的熔盐温度、换热器出口空气温度和浸入熔盐中深度的变化曲线如图4所示。换热器入口温度基本与室温保持一致，为10℃，出口初始温度为110℃，熔盐初始温度为450℃。释热开始后，盘管换热器逐渐浸入熔盐中，换热面积逐渐增大，换热器出口的空气温度迅速升高。释热136 s后，换热器出口空气温度逐渐稳定在200℃的目标温度。由于空气不断从熔盐侧取热，熔盐温度逐渐降低，换热器工作面积在PID控制的作用下也逐渐增加。在整个过程中，换热器出口温度能够基本稳定在200℃。当换热器下降至储热罐最底部无法继续下降时，换热器出口温度开始下降，释热结束。

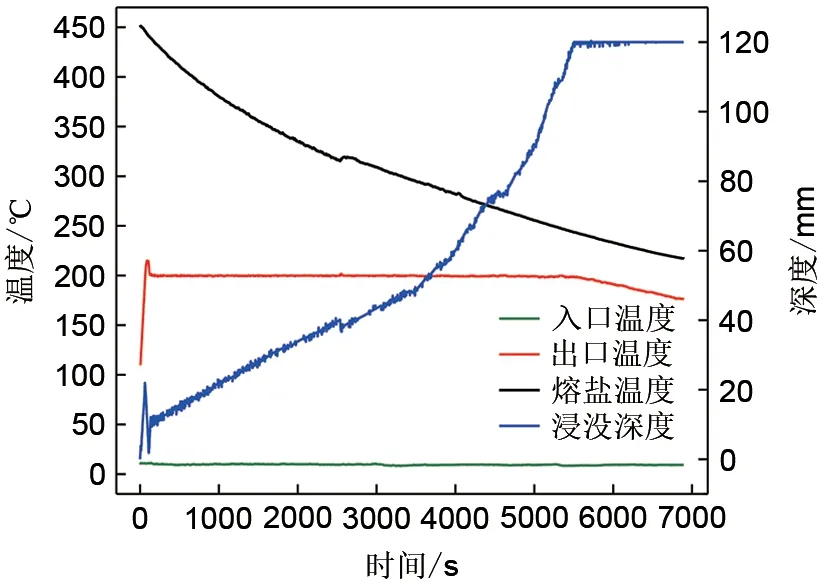
图4 C-c法释热过程曲线Fig.4 Heat release curve of C-c method

由Lopze整定方法控制下的实验结果如图5所示。释热初期，换热器浸入熔盐中的深度过大，导致出口空气温度高达271℃。由于出口空气温度已高于目标温度，换热器开始快速上升以减小换热面积。受到释热前期换热器大幅度移动的影响，直至释热290 s时，出口空气温度才逐渐稳定于200℃。虽然换热器出口空气温度在换热结束时略有波动，但其仍可以稳定在设定值。对于本方法而言，较大的调节幅度引起了释热始末的不稳定现象。

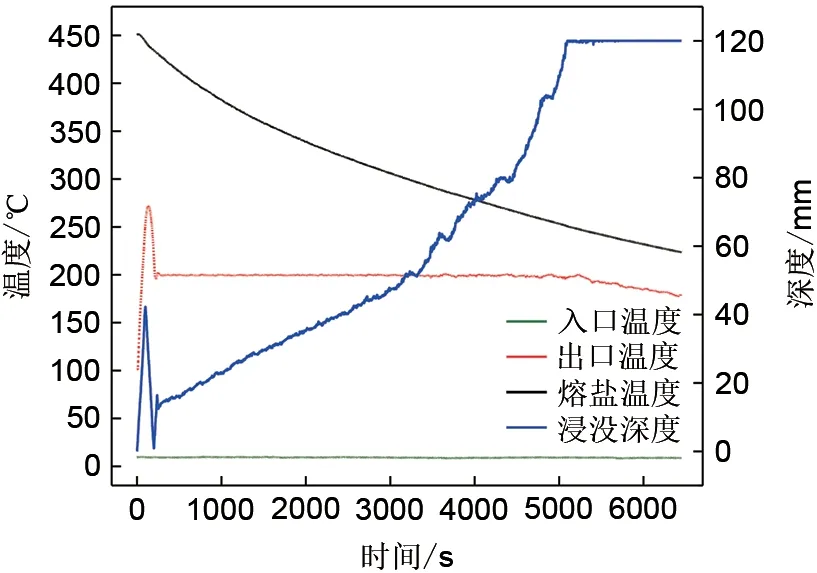
图5 Lopze法释热过程曲线Fig.5 Heat release curve of Lopze method

图6和图7分别展示了使用MCP法和Z-N法时熔盐温度、换热器进出口空气温度和浸入熔盐中深度的变化曲线。结果表明，使用上述两种PID整定方法调节换热面积时，熔盐温度在释热过程中缓慢下降，且温降速度越来越慢。采用MCP法时，换热器出口温度在首次达到200℃后便一直稳定于目标值，直至换热器浸没至储热罐最底端。对于Z-N法，虽然没有类似于Mcp法在达到目标值200℃后就保持稳定，但其最高温度仅升至203℃。在释热后期，熔盐温度低至248℃时，换热器浸入熔盐的深度变化剧烈，导致出口空气温度随之波动，因此导致整个释热过程提前结束。

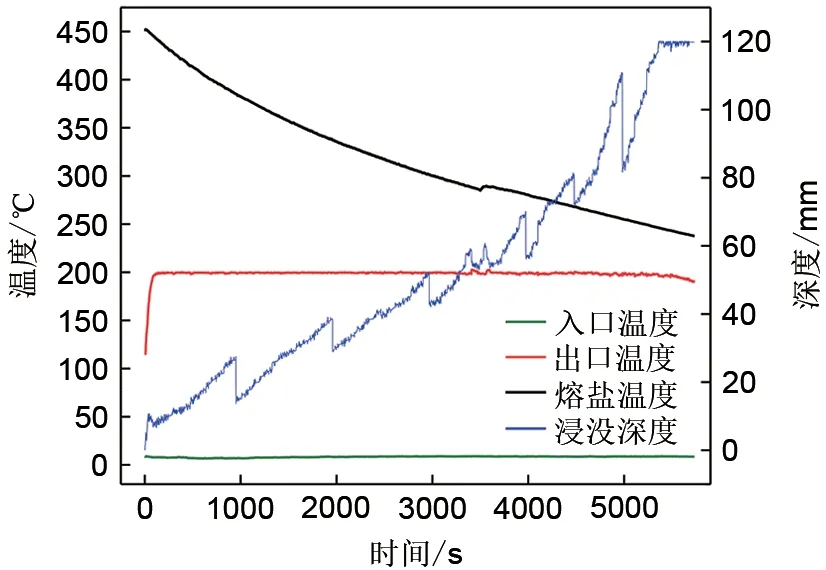
图6 Mcp法释热过程曲线Fig.6 Heat release curve of Mcp method

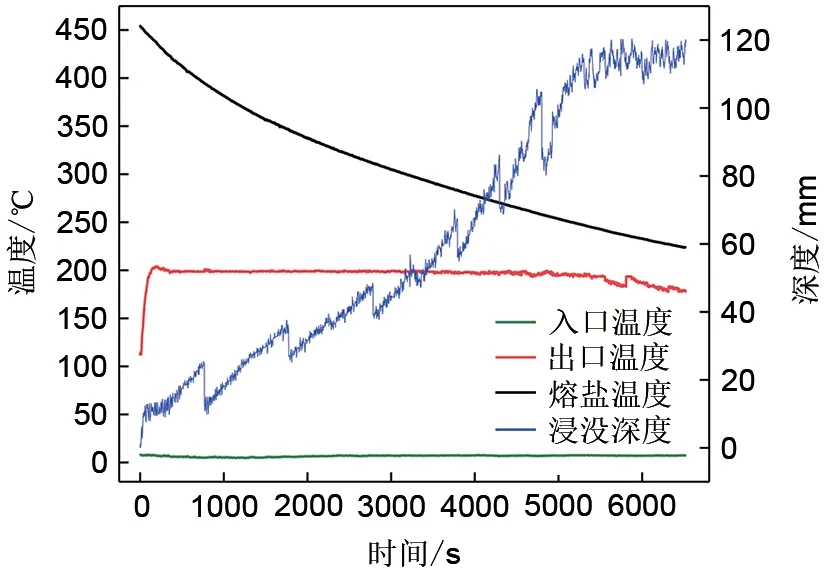
图7 Z-N法释热过程曲线Fig.7 Heat release curve of Z-N method

当使用不同整定方法对换热面积进行调节时，虽然释热过程中换热器的运动规律有所差异，但在四种整定方法对换热面积的控制下，换热器浸入熔盐中的深度均缓慢增加，熔盐温度缓慢下降，虽然换热器出口空气温度有所波动，但最终都能使换热器出口的空气温度稳定在目标温度的附近，并能够较长时间保持稳定，因此采用调节换热面积的方法能够实现稳定释热的要求。

2.2 释热功率稳定性分析

释热功率表示空气的取热功率，释热功率能够由式(4)计算

图8为四种整定方法下的释热功率。C-c法及Lopze法的释热功率先经历快速增大，达到最高点后再次迅速下降，最终稳定于164 W，在释热后期，释热功率无法保持稳定，开始缓慢下降；Mcp法与Z-N法的释热功率则是迅速增大至164 W，随后便开始保持稳定。Z-N法在实验后期其释热功率经历了一段衰减过程，随后又提升至164 W，但此现象并未保持很久，由于实验后期熔盐温度过低，释热功率无法再继续稳定在164 W。对于Mcp法而言，释热功率从首次达到164 W便一直保持稳定直至释热结束，由图中可以看出，Mcp法的释热功率曲线最为稳定。

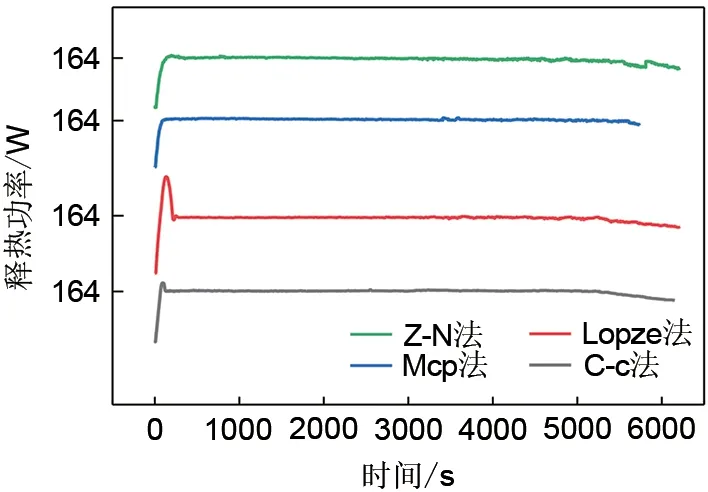
图8 不同方法下释热功率曲线Fig.8 Heat release power curves of different methods

2.3 释热时间及稳定释热时间分析

释热时间能够体现一个系统的释热效果，而稳定释热时间是指换热器出口空气温度能够稳定于目标温度的时间，其能够用来评价释热过程中的稳定效果。图9展示了四种方法下的释热时间及稳定释热时间。其中C-c法的释热时间为6895 s，稳定释热时间为5935 s；Lopze法的释热时间为6450 s，稳定释热时间为5443 s；Mcp法的释热时间为5734 s，稳定释热时间为5600 s；Z-N法的释热时间为6523 s，稳定释热时间为5435 s。尽管使用不同方法调节换热面积进行释热时的释热时间和稳定释热时间有所不同，但两者间差距并不大，在总释热时间中，较长的时间都能够使换热器出口的空气温度稳定于200℃的目标值，其中Mcp法的稳定释热时间高达总释热时间的97.66%，由此可见，使用调节换热面积的方法使换热器出口取热介质温度保持稳定具有较大的可行性以及良好的稳定效果。

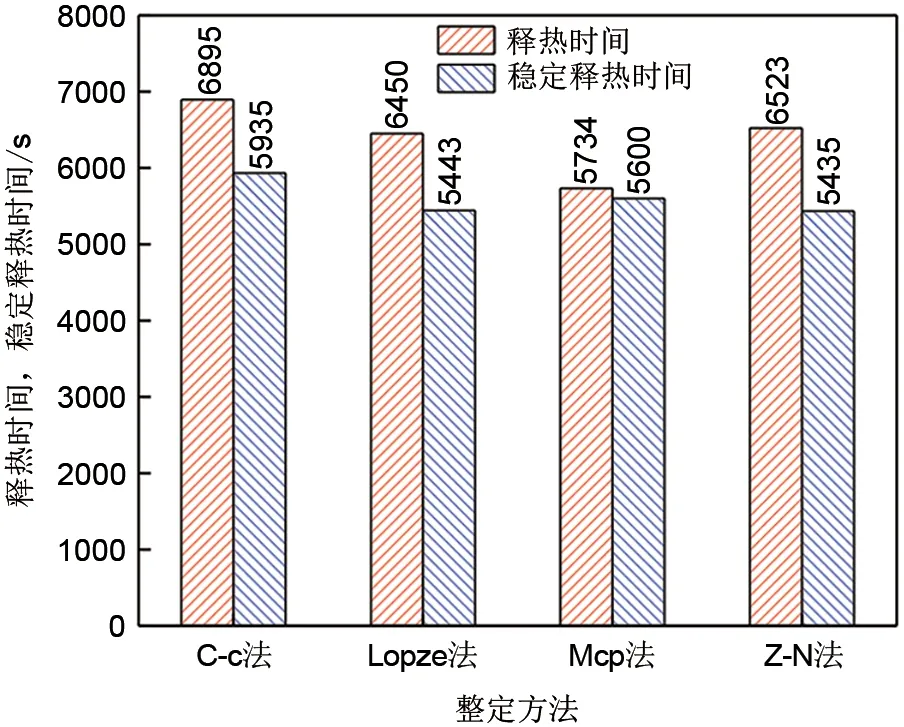
图9 不同方法下释热时间及稳定释热时间Fig.9 Heat release time and stable heat release time of different methods

2.4 释热量及有效释热量分析

由于㶲损失，蓄热罐中熔盐释放的热量不能完全取出，其中能够被取热介质取走的热量称为有效释热量，则释热量及有效释热量能够通过下式计算

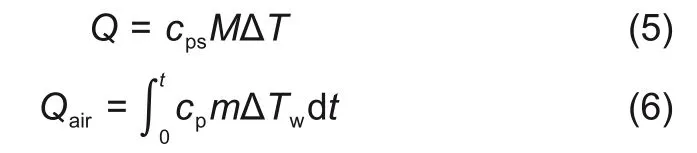
4种方法的释热量及有效释热量如图10所示。由图可见，使用C-c法的释热量和有效释热量均最高，为2447.48 kJ和1118.96 kJ；使用Mcp法时的释热量及有效释热量均最少，为2247.9 kJ和943.714 kJ；Lopze法和Z-N法的释热量2384.56 kJ和2426.47 kJ，有效释热量分别为1053.365 kJ和1066.194 kJ。由于换热器的上下移动，蓄热罐并未布置顶盖，因此产生了大量的热损失，当熔盐通过顶面向房间散发的热量一定时，足以看出C-c法在释热过程中产生额外热损失更少。而采用Mcp法时不仅有效释热量较少，其释热量也较少。对上述4种整定方法进行比较后，Mcp法的有效释热量占释热量比重最高，稳定效果最好。

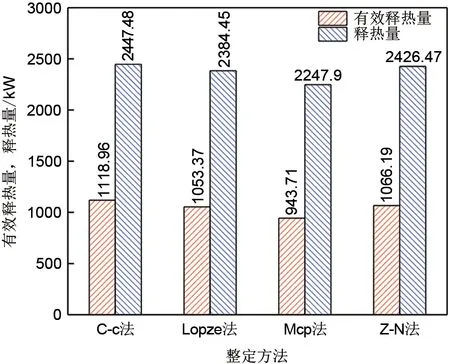
图10 不同方法下释热量及有效释热量Fig.10 Heat release and effective heat release under different methods

3 结 论

通过对换热面积进行调节，研究了单罐储热系统释热过程换热器出口取热介质温度的稳定性，并且分析了不同的PID整定方法调节换热面积时对单罐熔盐系统释热的影响。

（1）通过对换热面积的连续调节，能够实现换热器出口空气温度及释热功率的稳定。

（2）比较了使用C-c法、Lopze法、Mcp法和Z-N法四种PID整定方法调节换热面积时对释热过程的影响。采用Mcp法时，释热效果最稳定，稳定释热时间占总释热时间的97.66%。

符号说明

A——盘管换热器换热面积，m2

cps——熔盐比热容，kJ/(kg·K)

cp——空气比热容，kJ/(kg·K)

De——换热器浸没深度，mm

Di——蓄热罐内径，mm

Do——蓄热罐外径，mm

d——换热器直径，mm

H——蓄热罐高度，mm

Hbottom——蓄热罐底部厚度，mm

h——换热器高度，mm

K——增益，℃/mm

Kp——比例系数

L——换热器长度，mm

M——熔盐质量，kg

m——空气流量，kg/s

N——换热器圈数

T0——换热器浸没前出口温度，℃

T1——时间常数

Td——微分时间常数

Ti——积分时间常数

Tsta——稳定后换热器出口温度，℃

△T——熔盐释热前后温差，℃

△Tw——空气进出口温差，℃

p——盘管换热器螺距，mm

Q——释热量，kW

Qair——有效释热量，kW

q——释热功率，W

r——盘管换热器半径，mm

ρs——熔盐密度，kg/m3

λs——熔盐导热系数，W/(m·K)

τ——延迟，s