Co3O4/CoO氧化还原反应储/释热动力学特性

韩翔宇 ，王亮 ，葛志伟 ，凌浩恕 ，林曦鹏 ，陈海生 ,3，彭珑

（1中国科学院工程热物理研究所，北京 100191；2中国科学院大学，北京 100049；3中科南京未来能源系统研究院，江苏 南京 211135；4毕节高新技术产业开发区国家能源大规模物理储能技术研发中心，贵州 毕节 551712）

近年来，化石燃料资源逐渐枯竭以及温室效应等问题，使得可再生能源的发展逐步受到人们的关注[1-2]。太阳能具有清洁和资源丰富等优势，被认为是一种潜力巨大的可再生能源[3-4]。但是太阳能的大规模利用(如聚光太阳能热电厂)由于其间歇性受到限制。热化学储热具有高储能密度和储存周期在理论上不受限制的优势，是实现聚光太阳能热电厂连续运行的一种极具前景的技术[5-6]。中高温热化学储热体系分为金属氢化物体系、金属硫酸盐体系、金属碳酸盐体系、氢氧化物体系、金属氧化物体系、氨体系和有机物体系[2,7-8]。与其他6种热化学储热体系相比，金属氧化物体系具有以下优势[9-11]：中高能量密度、开环运行、运行温度区间与聚光太阳能热电厂相兼容。基于以上优势，本文选择了金属氧化物体系作为研究对象。

纯金属氧化物体系经过了广泛地研究，其中只有16种氧化物表现出氧化还原转化行为，可以在它们对应的温度区间内储放热。而考虑到材料成本、反应焓和反应温度等因素时，BaO2/BaO、Co3O4/CoO、Mn2O3/Mn3O4和CuO/Cu2O 4种纯金属氧化物体系表现出用于热化学储热的潜力[12]。

Wong等[12]发现BaO在再氧化过程中会形成BaO2灰层，从而降低其转化率。Hutchings等[13]测试了Co3O4的氧气吸收/释放特性，他们发现Co3O4粉末在870～955℃之间进行了100次氧化还原循环后没有反应性损失。Tescari等[14]制备了Co3O4包覆的陶瓷蜂窝，这些蜂窝在30个氧化还原循环中表现出完整的转化反应。Wong等[12]报道称Mn2O3的氧化速率很慢，并且氧化率远低于Co3O4。Karagiannakis等[15]实验发现Mn2O3颗粒储能密度非常低(仅有110 kJ/kg)并且其氧化反应动力学相当慢。Block等[16]研究了几种纯金属氧化物的氧化还原性能，CuO表现出较高的反应焓(650 kJ/kg)和最快的还原反应动力学(4.3 min)，如式(1)所示。然而，其再氧化反应缓慢，并且还原温度接近熔点，可能导致严重的烧结问题。Agrafiotis等[17]证明即使在最佳可行条件下，CuO在氧化还原实验后仍会严重烧结。上述四种纯金属氧化物体系对比如表1所示[12,16,18-19]。Co3O4/CoO体系具有最高的理论储能密度和良好的反应特性，在热化学储热应用方面最具发展前景，该体系的反应方程式如式(2)所示。

表1 四种纯金属氧化物体系对比[12,16,18-19]Table 1 Comparison of four pure metal oxide systems[12,16,18-19]

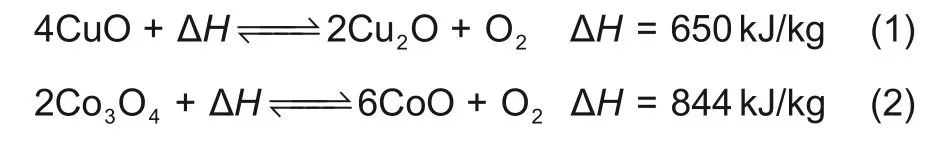
在Co3O4/CoO体系的反应动力学特性方面，Hutchuings等[13]研究发现Co3O4还原反应在空气和氧气中的活化能分别为439和892 kJ/mol，可用基于热力学驱动力的模型描述。Wong等[12]在不同加热速率下研究了Co3O4的还原反应过程，分析结果表明该反应符合3D成核收缩核模型，得到活化能为960 kJ/mol。Muroyama等[20]在等温条件下实验研究了Co3O4的还原反应，他们提出可用Avrami-Erofeyev模型来描述该反应过程，其中Avrami-Erofeyev常数n=1.968，等温反应的活化能为247.21 kJ/mol。

然而，目前对于不同条件下的Co3O4还原反应动力学研究较少，尤其缺少非等温条件下的还原反应过程的精确描述。本文测试和分析了氧浓度和加热/冷却速率对Co3O4/CoO体系反应动力学特性的影响，研究了不同加热速率下的还原反应特性，分析了其还原反应动力学机理，并得到较为精确的还原反应动力学模型，为基于金属氧化物体系的热化学储热单元设计提供理论依据。

1 研究方法

本文利用同步热分析仪对Co3O4/CoO体系的氧化还原特性进行了实验研究，并采用主图法和Friedman法分析了其还原反应动力学。

1.1 实验方法

实验所用材料为纯Co3O4粉末(阿拉丁，≤6μm)，取约5 mg样品置于Al2O3坩埚中利用STA 449 F3 Jupiter同步热分析仪进行热重分析(TGA)和差式扫描量热(DSC)实验，图1中显示了加热/冷却速率为10 K/min时的温度-时间曲线。

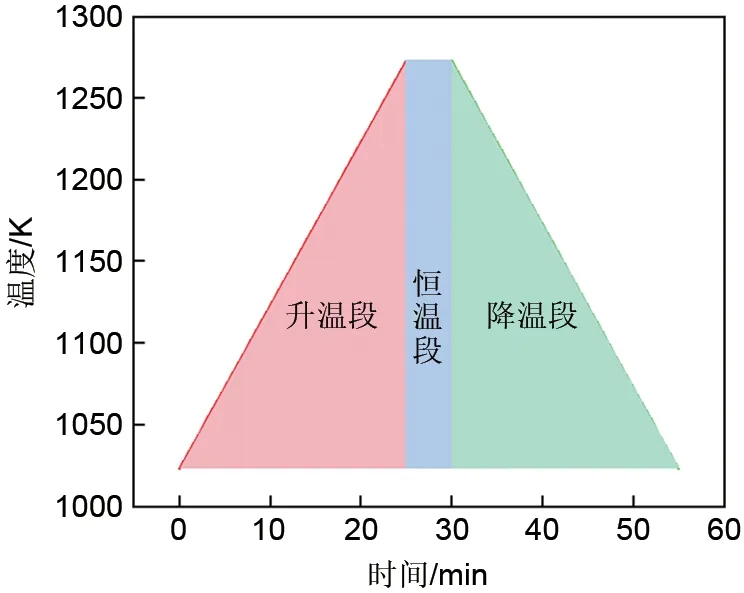
图1 加热/冷却速率为10 K/min时的实验曲线Fig.1 The experimental curve when the heating/cooling rate is 10 K/min

首先选择不同的氧浓度在1023～1273 K温度区间内进行热循环实验，升温过程中选择0、10%、20%、30%、40% O2-Ar进行Co3O4的还原，降温过程中选择10%、20%、40%、60%、80% O2-Ar进行CoO的氧化。实验中加热/冷却速率为10 K/min，气体流量为100 mL/min。之后，在20% O2-Ar(气流量为100 mL/min)下选择7.5、10、15、20 K/min加热/冷却速率在1023～1273 K之间进行热循环实验，研究加热/冷却速率对氧化还原反应的影响。

通过改变氧浓度和加热/冷却速率，研究了不同的实验条件对Co3O4/CoO体系氧化还原特性的影响。之后，对不同加热速率下的还原反应进行动力学分析。

1.2 动力学分析方法

固-气反应的反应速率可以由式(3)所示的反应速率方程表示[21]

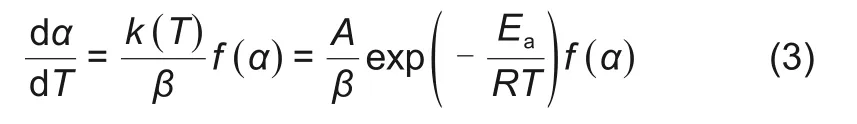
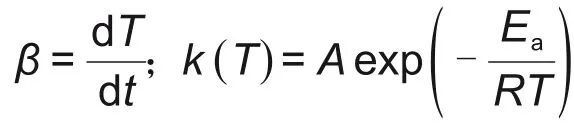
表2 常用的固态动力学机理模型[22]Table 2 Mechanism model of solid state kinetics[22]

首先利用主图法[23]进行反应机理模型的选择，取α=0.5为参考点得出

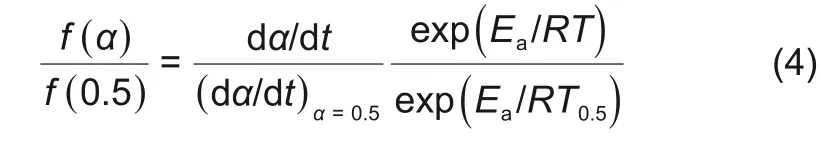
其中，T0.5为α=0.5时的反应温度。

利用Friedman方法[24]得到活化能和指前因子，对式(3)取对数得

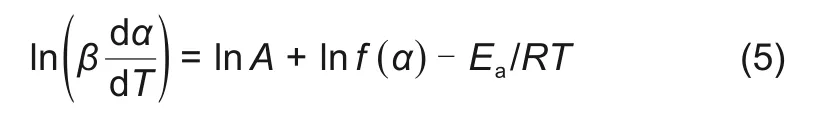
在不同的加热速率下，采用主图法和Friedman法对还原反应进行了详细的分析，从而得到反应动力学机理方程。

2 结果和讨论

2.1 实验结果讨论

本文研究了氧浓度和加热/冷却速率对Co3O4/CoO体系反应温度、反应速率和反应焓的影响。

不同氧浓度下的氧化还原反应转化率变化如图2所示。如图3所示，对于还原反应来说，提高氧浓度可以提高反应的起始温度，从而提高热力学驱动力，使得最大反应速率也随之提高。当氧浓度为20%时，最大反应速率是氧浓度为0时的近3倍。然而，随着氧浓度的进一步提高，也就是生成物气体浓度的提高又在一定程度上抑制了温度升高对于该反应的有益影响。与还原反应类似，随着氧浓度的提高，氧化反应的起始温度也随之提高，而最大反应速率随着氧浓度的提高而提高且没有出现降低的趋势，这受到热力学驱动力的提高和反应物气体浓度的提高的有益影响。在不同氧浓度下材料的转化程度相近，因而如图4所示，不同的氧浓度对还原反应焓没有明显地影响。

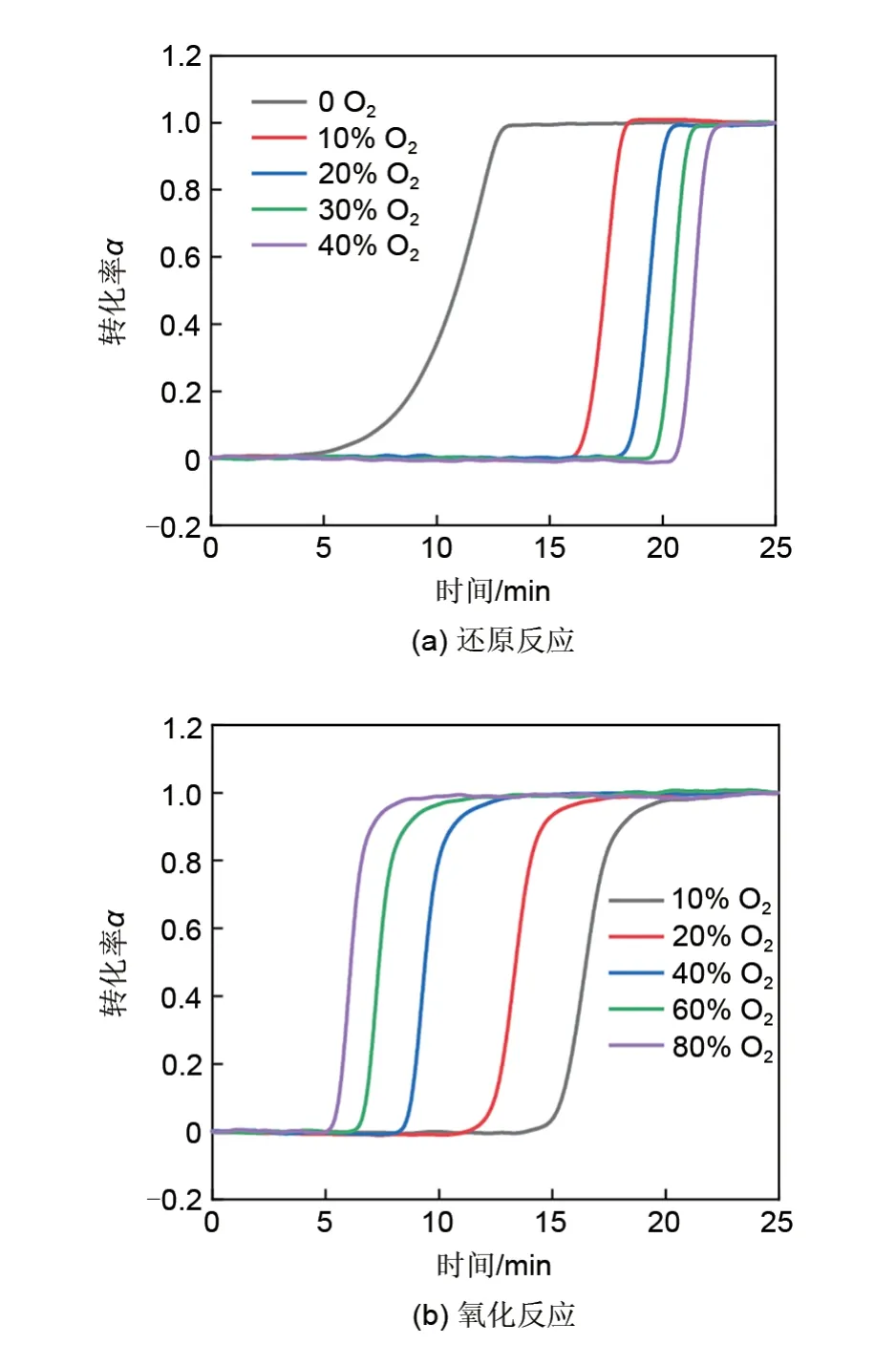
图2 不同氧浓度下的氧化还原反应转化率-时间图Fig.2 Conversion rate-time plots of redox reaction under different oxygen concentration

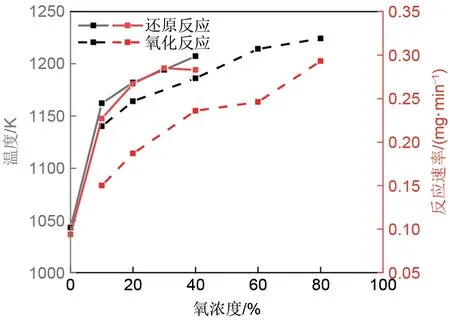
图3 不同氧浓度下的氧化还原反应过程Fig.3 Redox reaction process under different oxygen concentration

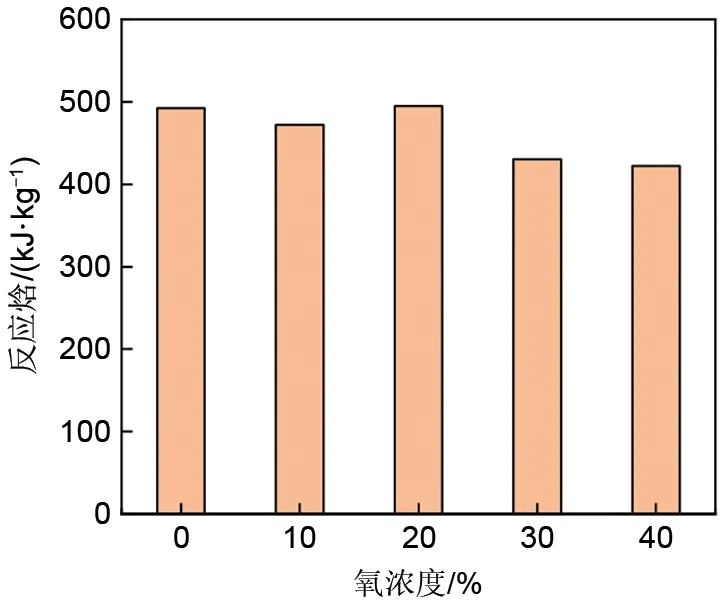
图4 不同氧浓度下的还原反应焓Fig.4 Enthalpy of reduction reaction under different oxygen concentration

图5为不同加热/冷却速率下的氧化还原反应转化率变化，不同加热/冷却速率下的最大反应速率值见图6。由图6可知，随着加热/冷却速率的提高，氧化还原速率均随之提高，这可能与热力学驱动力的增加有关。此外，氧化反应速率明显慢于还原反应速率，因而也使得其成为整个循环的限制步骤。与不同氧浓度下的还原反应结果类似，由图7可知，加热速率对还原反应焓没有明显影响。

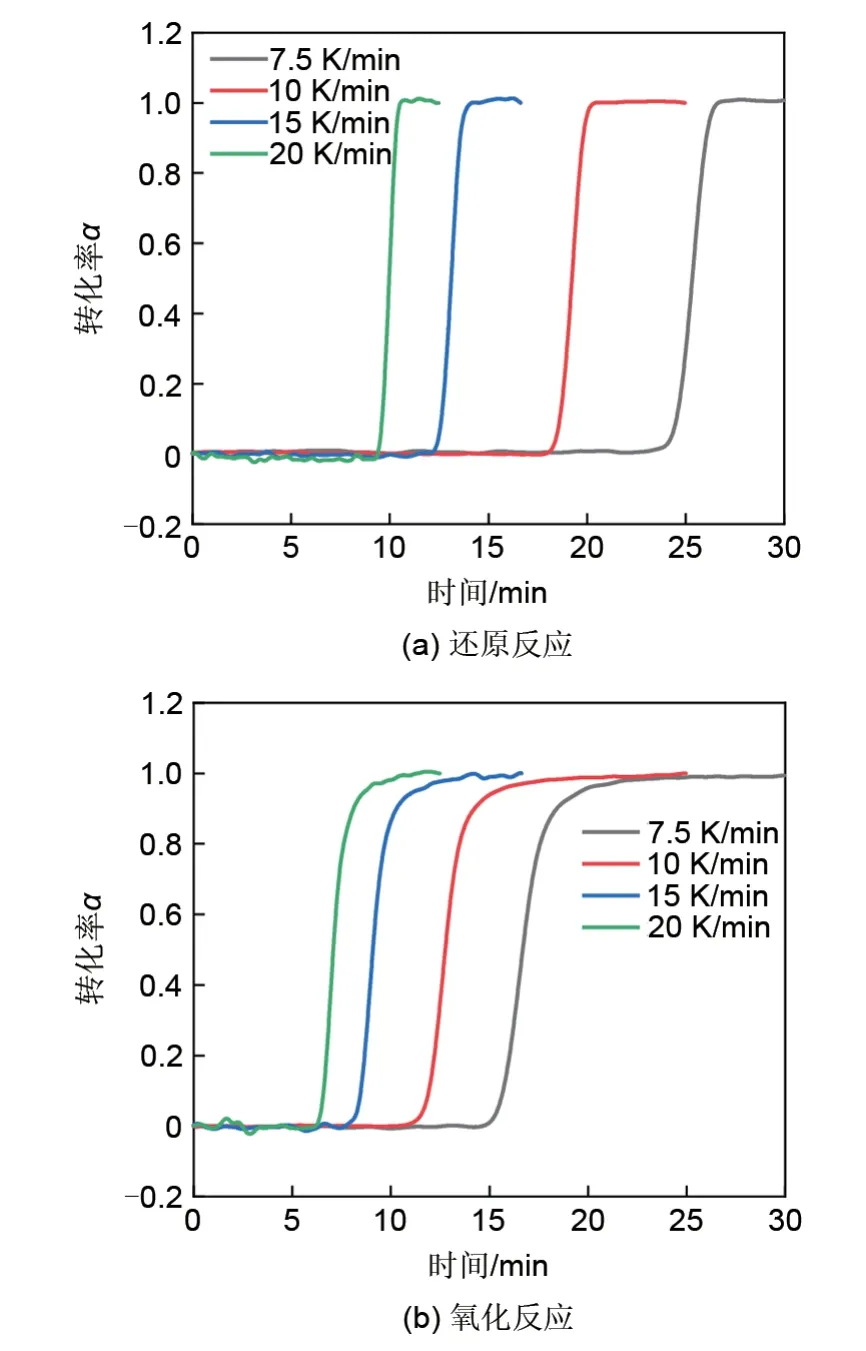
图5 不同加热/冷却速率下的氧化还原反应转化率-时间图Fig.5 Conversion rate-time plots of redox reaction under different heating/cooling rates

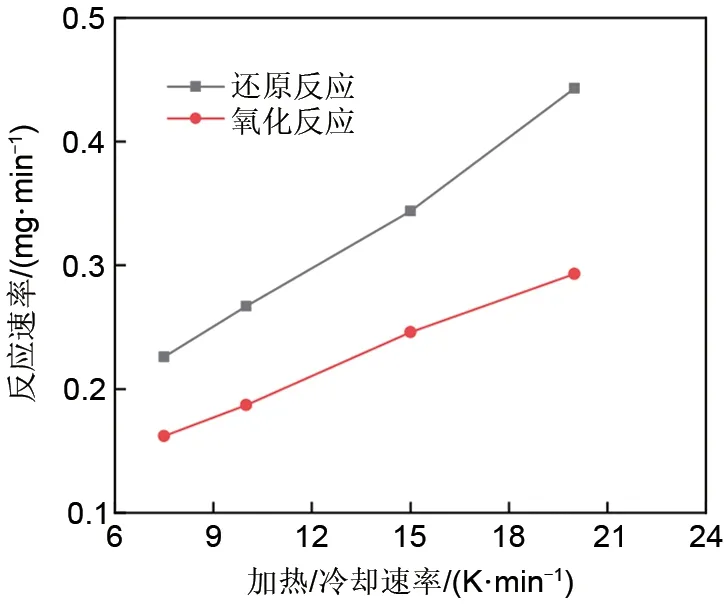
图6 不同加热/冷却速率下的氧化还原反应速率Fig.6 Redox reaction rate under different heating/cooling rates

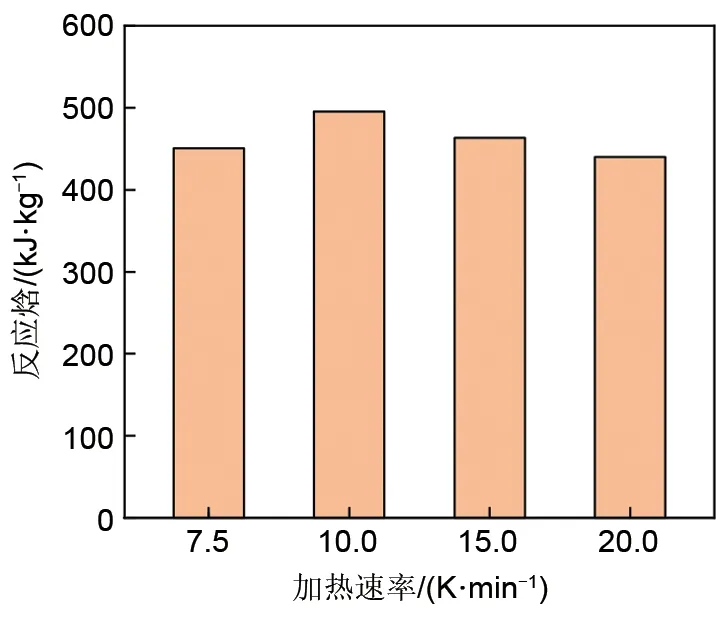
图7 不同加热速率下的还原反应焓Fig.7 Enthalpy of reduction reaction at different heating rates

2.2 还原反应动力学分析

本文测试了加热速率为7.5、10、15和20 K/min时的还原反应，反应动力学分析如下。

利用Friedman方法(图8)得到转化率α在0.675～0.950之间的活化能，如图9所示。由图9可知，还原反应活化能Ea随α增大而降低，其平均值Ea=1285.777 kJ/mol。

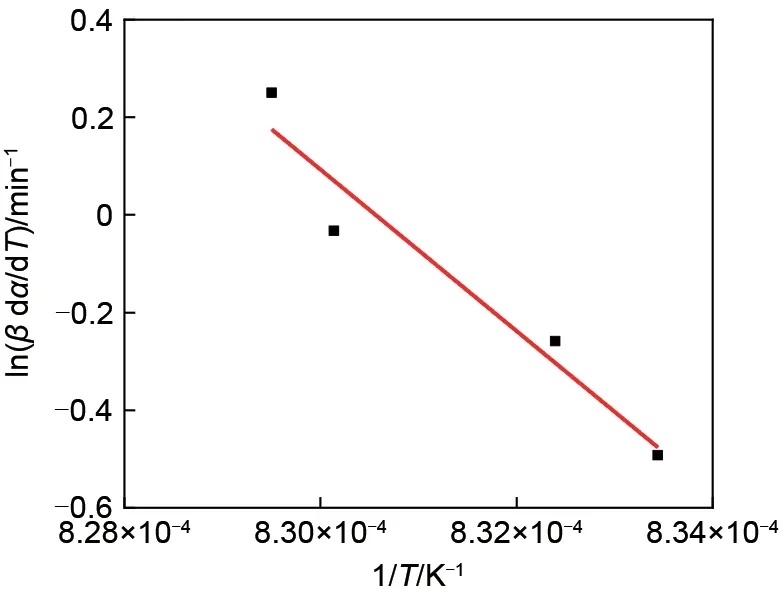
图8 还原反应在α=0.7时的Friedman图Fig.8 Friedman plot for the reduction reaction atα=0.7

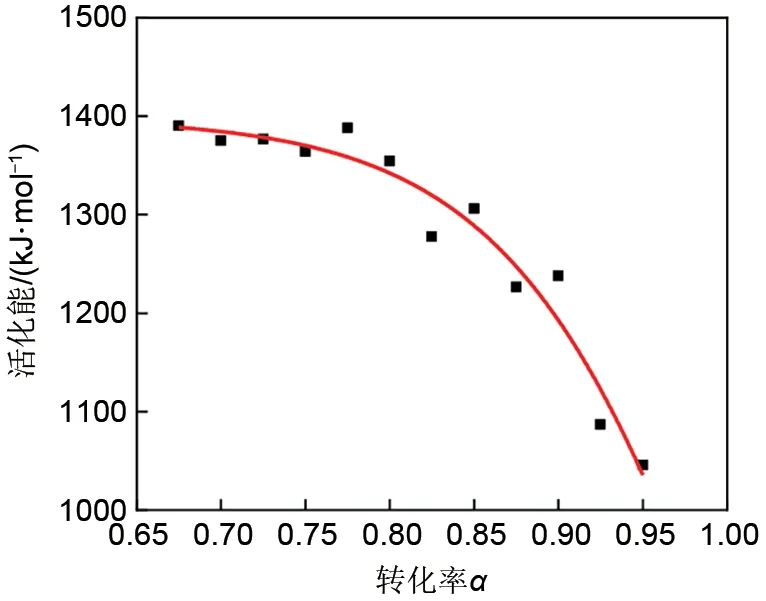
图9 不同转化率时的活化能值Fig.9 The activation energy values at different conversion rates

之后，利用主图法进行反应机理模型的选择。将4个加热速率下的实验数据和由Friedman法计算得出的反应活化能平均值代入到式(4)中，得到如图10所示的微分形式的主图。如图10(a)所示，仅有A2、A3、A4和B1模型具有和实验数据相同的趋势，所以图10(b)，10(c)和10(d)中仅对比了这四个模型和实验数据曲线。从图10中可以看到，实验数据与随机成核模型Avrami-Erofeyev(A2)最为接近，因而还原反应可以用成核与核生长机理描述。由于杂质、表面、边缘、错位、裂纹和点缺陷的存在，晶体的局部能量会因缺陷而波动。这些点的反应活化能是最小的，因此它们被称为成核点。当Co3O4被加热到还原反应所需的温度时，CoO首先在这些点成核，随着反应的进行CoO核生长并伴随着新核的形成。最终还原反应完成，Co3O4被还原为CoO。

由于样品粒径分布以及形状的不均匀性，使得实际过程并不能完全符合理想模型[25]。由图10可知，实验数据与机理模型之间存在着一定的偏差，且该偏差随着加热速率的升高而变大。因而对Avrami常数n进行了优化计算，图11显示了在不同加热速率下，Co3O4还原反应的实验数据和模型预测结果的比较。其中，n=1.09653±0.00286，模型与实验结果符合较好。从而得到还原反应动力学模型，如式(6)所示

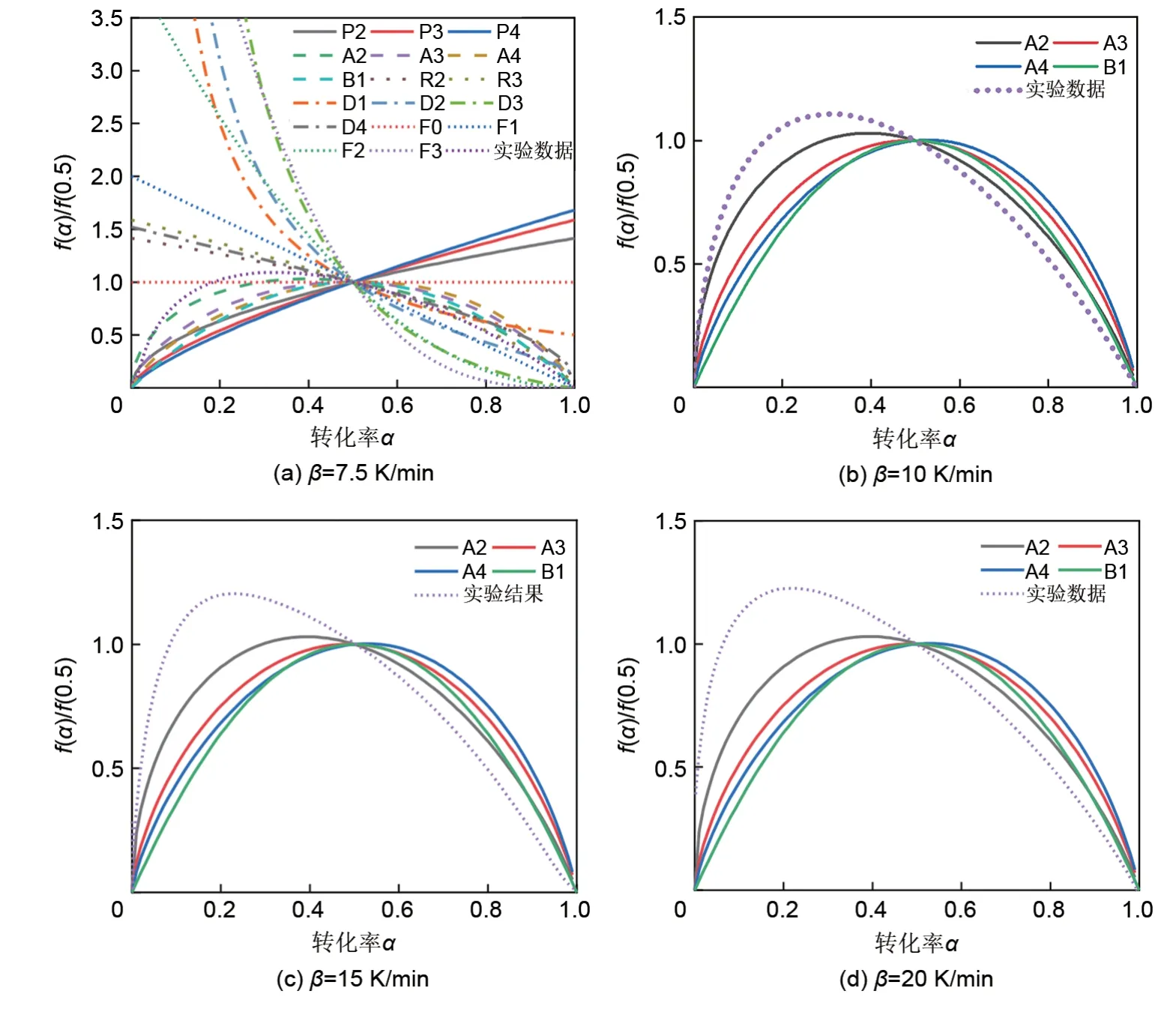
图10 还原反应的主图法分析Fig.10 Master plot analyses for the reduction reaction

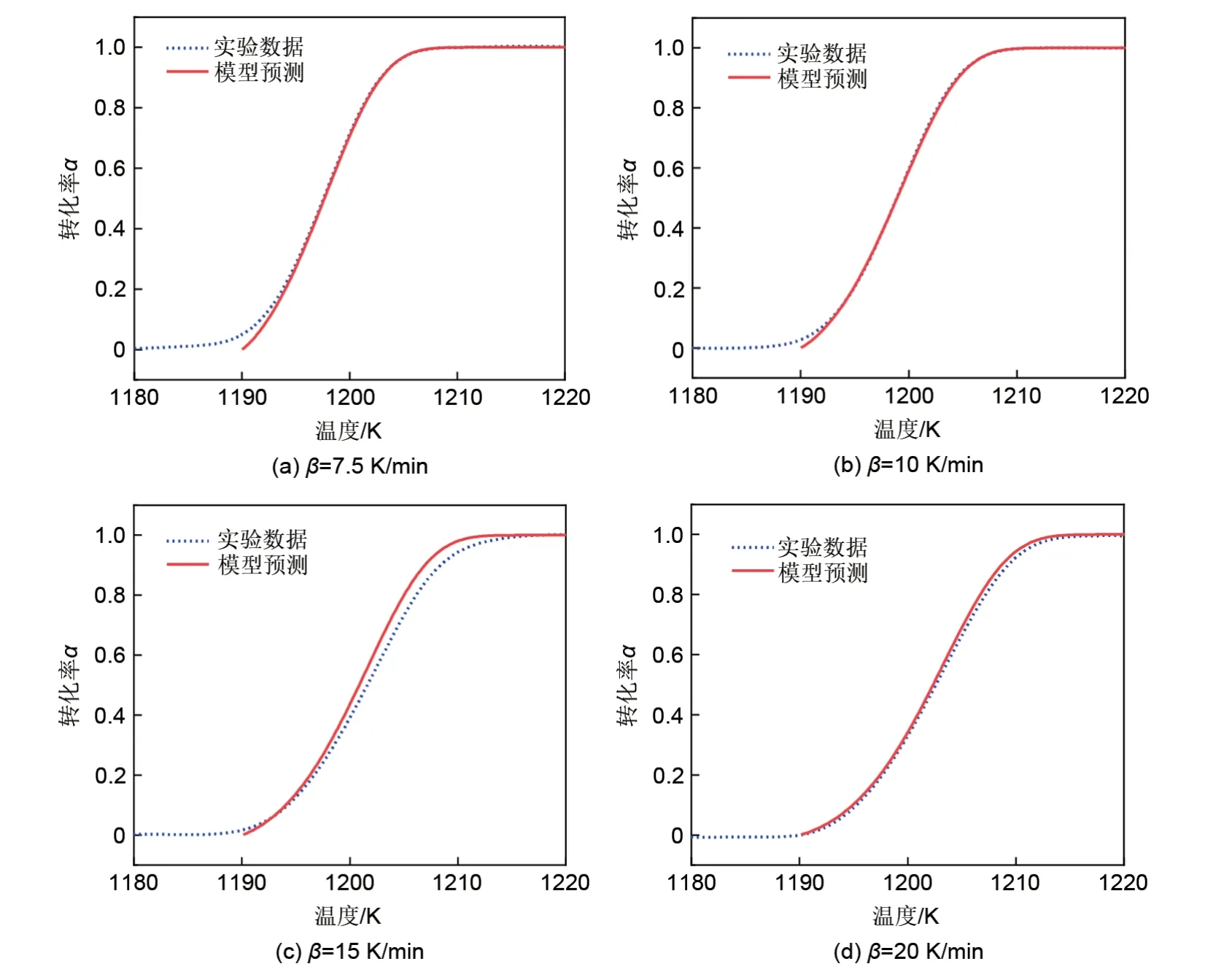
图11 还原反应的模型预测结果Fig.11 Modelling result for the reduction reaction

3 结 论

本文以Co3O4/CoO热化学储热材料作为研究对象，采用了热重分析和差示扫描量热法对该体系的氧化还原反应过程进行了研究。

（1）不同氧浓度下的实验结果表明，氧化还原反应的起始温度随氧浓度的增加而增加，对于还原反应来说，随着氧浓度的增加其最大反应速率先增加而后趋于平缓，对于氧化反应来说，其最大反应速率随氧浓度的增加而持续增加。氧浓度对还原反应焓没有明显影响。

（2）不同加热/冷却速率下的实验结果表明，随着加热/冷却速率的提高，还原反应和氧化反应的最大反应速率均随之增加。而对于还原反应焓来说，加热速率对其没有明显影响。

（3）动力学分析结果显示，还原反应动力学可以用成核与核生长机理描述，符合随机成核模型Avrami-Erofeyev(A2)，活化能值为1285.777 kJ/mol。由于实验数据和机理模型之间存在一定的偏差，因而对机理模型参数n进行了优化计算，得到了较为精确的还原反应动力学方程。