关于导体棒“稳定速度”的正确理解

余兴科

(重庆市垫江教师进修学校 重庆 408300)

在求解物理问题时，学生经常被一些表面现象所迷惑，生搬硬套，盲目类比，得出错误结论。其原因是没有掌握发生现象的实质，没有真正理解题目的意思，对知识的本质含义不清。在电磁感应现象中，导体棒切割磁感线运动而产生感应电流，在安培力作用下最后匀速运动达到稳定，求稳定速度，学生很容易出错，下面用三道例题加以分析。

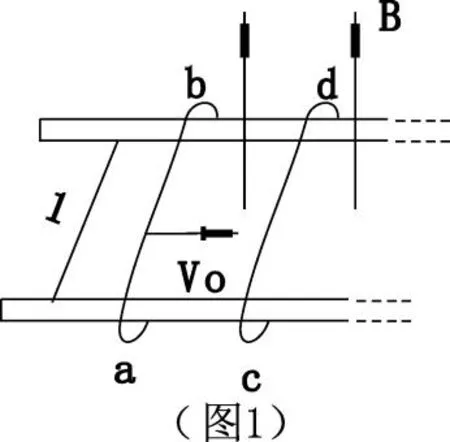
例1：两根足够长的固定的平行金属导轨位于同一水平内，两导轨间的距离为1，导轨上面横放着两根导体棒ab和cd构成矩形回路，如图1所示，两根导体棒的质量皆为m，电阻皆为R，磁感应强度为B，设两导体棒均可沿导轨无摩擦地滑行，开始时，棒cd静止，棒ab有指向棒cd的初速度V0（如图所示），若两导体棒在运动中始终不接触，求：

（1）在运动中产生的焦耳热最多是多少？

解析：ab棒向cd棒运动时，两棒和导轨构成的回路面积变小，磁通量发生变化，于是产生感应电流，ab棒受到与运动方向相反的安培力作用做减速运动，cd棒则在安培力作用下做加速运动，在ab棒的速度大于cd棒的速度时，回路中总有感应电流，ab棒继续减速，cd棒继续加速，两棒速度达到相同后，回路面积保持不变，磁通量不变化，不产生感应电流，不产生焦耳热，以后两导体棒速度稳定，以相同的速度做匀速运动。

也可这样理解：当ab棒向右运动切割磁感线产生感应电动势，回路的感应电流受安培力使ab减速，cd加速，同时cd棒产生感应电动势在回路中与ab棒产生的感应电动势相反，所以随着速度增加，回路中感应电流减小，当两棒速度相等时，电流为零，安培力为0，匀速运动。

（1）从初始至两棒达到速度相同的过程中，两棒安培力始终大小相等，方向相反，合力为零。两棒的总动量守恒，有mv0=2mv

根据能量守恒，整个过程中产生的总热量

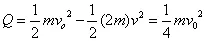
此时回路中感应电动势和感应电流分别为：

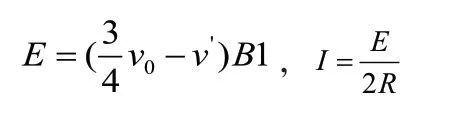
总结：从以上分析知，两棒速度稳定的实质是合力为0，即电流为0，而不是速度相等。

例2：如图2所示，两平行光滑导轨处于竖直向上的匀强磁场中，左边部分的宽度是右边部分宽度的两倍，金属棒ab、cd质量分别为2m，m静置于左右两导轨上。现给ab瞬时冲量，求cd的稳定速度。（两导轨足够长）

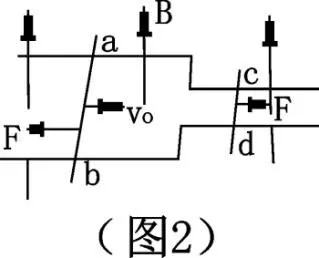
分析与解：ab获得速度v0向右运动，切割磁感线，在回路产生感应电流，于是受安培力作用，ab棒向右减速，cd棒开始向右加速，同时cd棒切割磁感线产生感应电动势，由右手定则之其方向在回路中与ab产生感应电动势相反。E=B21vab-B1vcd，随着vab减小，vcd增大，回路中电流减小，安培力减小，当E=0，即B21vab-B1vcd=0时，回路中电流为0，安培力为0，两棒匀速运动，速度稳定，所以稳定后

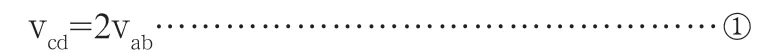
设开始运动到稳定过程中，回路中平均电流为I，所用时间为△t，则对两棒分别用动量定理有：

由①、②、③解得

点评：不少人利用例1的结论，认为稳定后两棒速度相等，系统动量守恒，其原因就是没有正确理解“稳定速度”的实质，例2中两棒受安培力的合力不为零，所以不能用动量守恒定律。

例3：两根足够长的、固定的平等金属导轨位于同一斜画内，两导轨间的距离为l，导轨上面横放着两根导体棒ab和cd，构成矩形回路，如图3所示，两根导体棒的质量皆为m、电阻皆为R，回路中其余部分的电阻可不计，假设未加磁场时两棒均能在斜面上匀速下滑，现在整个导轨平面内加上垂直斜面向上的匀强磁场，磁感应强度为B，开始时，棒cd静止，棒ab有沿斜面向下的初速度v0，若两导体棒在运动过程中始终不接触，且导体棒与导轨间的最大静摩擦力等于滑动摩擦力，则：

（1）两导体棒在运动中产生的焦耳热最多是多少？

解：无磁场时，两棒匀速下滑，则重力、弹力、摩擦力三力的合力0，滑动过程中安培力方向沿斜面不改变支持力。所以在滑动过程中两棒相当于只受安培力作用，且大小相等，方向相反，系统动量守恒。稳定时两棒速度相等，以后匀速运动，与例1解法完全相同。

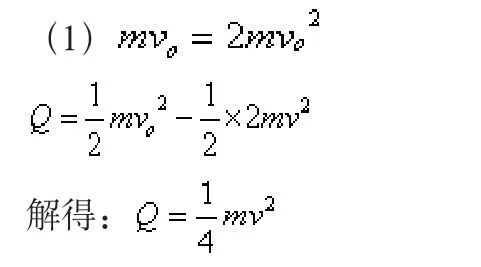
综上所述，两金属棒在导轨运动达稳定速度的实质是回路中电流（电动势）为0，安培力为0，而不是两棒速度相等，也不能乱套动量守恒公式。