基于等效噪声模型的数字锁相环环路参数确定方法
封帆,龚航,臧文驰,陈华明
( 国防科技大学电子科学学院,长沙 410073)
0 引言
守时是高精度时间频率和授时服务的核心和基本内容.然而原子钟的短期频率稳定度会因为迪克效应[1]以及器件噪声等因素的影响而降低. 锁相环(PLL)是产生频率信号的一种闭环自动控制系统,它能实时跟踪并输出频率信号.在锁定状态时,PLL环路能够净化输出相位噪声功率谱的纯度,并提高频率稳定度.
PLL 环路参数的选取直接影响其输出的相位噪声功率谱和频率稳定度.对于PLL 的仿真建模,文献[2]基于幂律谱模型提出了一种差别于仿真电路模拟器(SPICE)仿真模型的PLL 建模方法.在建立PLL模型后,可以为PLL 的性能、面积和功耗做出初步的估计.该方法相对于常规的SPICE,仿真模型大幅提升了仿真速度.对于环路参数的选取,文献[3]和文献[4]基于常规的PLL 噪声模型,通过推导整个环路输出相位噪声方差公式,再对其求极小值,得到最佳环路参数.文献[5]和文献[6]对用于GPS接收机的PLL 进行分析.文献[5]将PLL 等效为维纳滤波器来设计PLL 参数,文献[6]以跟踪误差标准差为指标对PLL 参数进行分析.文献[7]和文献[8]提出了一种等价于Kalman 滤波器的数字PLL 环路参数确定方法.该方法根据输入信号和压控振荡器(VCO)信号的相位噪声交点设置环路参数(下文简称直接计算交点法),使得输入信号与VCO相位噪声的交点等于PLL 系统传递函数与误差传递函数的交点,并得到了较好地频率稳定度.
以上研究对PLL 环路参数的选取提供了指导.直接计算输入信号和VCO信号的相位噪声交点以确定环路参数的方法尽管简单,但其计算过程没有考虑到PLL 的模块噪声,只考虑了PLL 输入信号和VCO信号的相位噪声,因此仅适用于理想PLL模型.为了解决这个问题,本文综合考虑PLL的模块噪声,提出一种基于等效噪声模型的数字PLL 最佳环路参数确定方法.通过PLL 传递模型和相位噪声的幂律谱[9-11]将数字PLL 各项噪声叠加到输入和VCO信号上,使整个PLL只存在等效输入噪声和等效VCO噪声,简化了PLL 的噪声传递模型,从而可以使用直接计算交点的方法确定最佳环路参数并解决了直接计算交点法来考虑模块噪声的问题,使用文中方法得到的环路参数可以较好地贴合理论结果.
1 传统环路参数确定方法
使用PLL 提高频率稳定度的原理主要是利用PLL 的滤波性能,净化输出信号的相位噪声.为了降低PLL输出的相位噪声,传统的环路参数确定方法主要分为两类:一类通过选择环路参数,使得输出的相位噪声方差最小;另一类是一种近似方法,根据环路特性和近端相噪与远端相噪的要求,确定环路参数.
1.1 基于相位噪声方差的环路参数选取方法
传统PLL 的基本噪声模型如图1所示.

图1 PLL 噪声传递模型


理论上,为了得到一个较好的相位噪声,通常要使总相位噪声方差最小.所以一般用式(7)对环路参数求导,并令导数为零,求解最佳参数. 但是相位噪声谱通常比较复杂,通过解析式计算并进行优化通常是不可行的.
1.2 直接计算交点法
工程上,一般直接测量输入信号和VCO信号的相位噪声功率谱的交点,并将其设为环路带宽,以获得较好的相位噪声.然而,常见的环路带宽都是在不同的条件下提出的,如环路噪声带宽BL是在输入噪声为白噪声(WN)的特殊情况下定义的.因此将环路带宽设为功率谱的交点频率并不能得到较好的相位噪声性能.
在此基础上,有学者利用环路传递函数对这种方法进行改进.
在理想情况下,可以认为PLL 只有输入噪声和VCO噪声,那么PLL 输出信号的相位噪声θo的功率谱为

根据1.1节,PLL 对于输入信号的相位噪声起到低通滤波作用,对于VCO 起到高通滤波作用.因此,文献[7]和文献[8]提出将PLL 系统传递函数H(z)与误差传递函数He(z)的交点频率记为f1,将输入噪声功率谱Sref(f) 和 VCO噪声功率谱SVCO(f)的交点记为f2.调整环路参数,当f1=f2时输出噪声最优地结合了输入噪声和VCO噪声的低相噪部分,如图3所示.图2为一个二阶PLL传递函数的幅频响应曲线.在该PLL 模型下,通过直接计算交点f1和f2得到最佳的环路参数.图3为该PLL 输出的相位噪声.可以看到该方法充分利用了PLL 的滤波特性,输出的相位噪声既能保持输入信号的近端低相噪特性,也能保持VCO信号的远端低相噪特性,输出的相位噪声性能较好.

图2 PLL的幅频响应曲线

图3 PLL 输出信号的单边带相位噪声
然而,在图1的PLL模型下,输出噪声的功率谱如式(5)所示.此时直接计算交点所设计的环路参数没有考虑到模块噪声的影响,输出的性能也不是最佳.因此,直接计算交点法只适用于理想情况,不能应用于带有模块噪声的PLL 模型.
对比式(5)与式(8)可以发现,如果将模块噪声等效到输入噪声和VCO噪声中,生成等效输入噪声模型和等效VCO噪声模型,就可以将式(5)简化为式(8)的形式.再根据直接计算交点法的原理,就能得到最佳的环路参数.
因此文中接下来将介绍PLL 等效噪声模型的建立方法,并基于等效噪声模型确定环路的最佳参数.
2 数字PLL的等效噪声模型
本节从PLL 模型出发,将鉴相器噪声等带内噪声等效到输入信号的相位噪声中,将环路滤波器噪声、数模转换器(DAC)噪声等带外噪声等效到VCO信号的相位噪声中,从而得到等效输入噪声模型和等效VCO噪声模型,并给出等效噪声模型的幂律谱参数计算公式.
2.1 等效输入噪声的建模
由于输入噪声和鉴相器噪声在环路中都为带内噪声,因此可以将鉴相器噪声叠加到输入噪声中,简化PLL 噪声传递模型.
在数字PLL 中通常使用TIC方法测量时间间隔,如图4所示.一般用计数器计算两个开关门信号之间的参考时钟所走的周期数N,再乘以参考周期Tref即可得到测量结果.然而由于参考时钟频率不够高,在测量时无法精确得到开/关门信号与下一个参考时钟上升沿的间隔时间ΔT1和 ΔT2,继而引入测量误差[14].引入的误差相当于一个量化器输出的量化误差,因此可以将该误差等效为在参考时钟周期Tref内均匀分布的WPM,而且输入噪声与鉴相器误差相互独立、互不相关[15].

图4 TIC测量原理


图5 等效建模前PLL噪声传递模型

图6 等效建模后PLL噪声传递模型
由于相位噪声基本是随机噪声,并没有严格的时域表达式,因此建立等效噪声模型需要计算其功率谱以及幂律谱参数.根据式(11)该等效输入噪声的相对时间起伏的功率谱为

2.2 等效VCO噪声的建模
由1.1节可知,LPF噪声、DAC噪声和VCO噪声都为带外噪声,受到环路的高通滤波作用,因此本小节将LPF噪声、DAC噪声与VCO噪声相叠加,生成等效VCO噪声,简化PLL 噪声模型.
本文的分析基于数字PLL,因此环路滤波器为纯数字电路,抗干扰能力很强;另一方面,由于DAC位数有限,其输出的电压有明显的量化效应.因此,相对于环路滤波器的微弱噪声,文中主要考虑DAC噪声.
DAC噪声可以视为符合均匀分布的量化WN,因此该WN 会以压控电压的形式作用于VCO.VCO模型相当于一个积分器,量化WN最终转化为WFM影响输出信号的频率稳定度[16].考虑到DAC的量化噪声与VCO的相位噪声互不相关,因此该过程可以等效如图7所示.

图7 DAC噪声在VCO中的传递模型

与2.1的分析方法相似,由式(3)~(4),可以得到LPF噪声、DAC噪声与VCO噪声的系统传递函数的关系为
图9为得到等效VCO噪声后,PLL 的噪声传递模型.
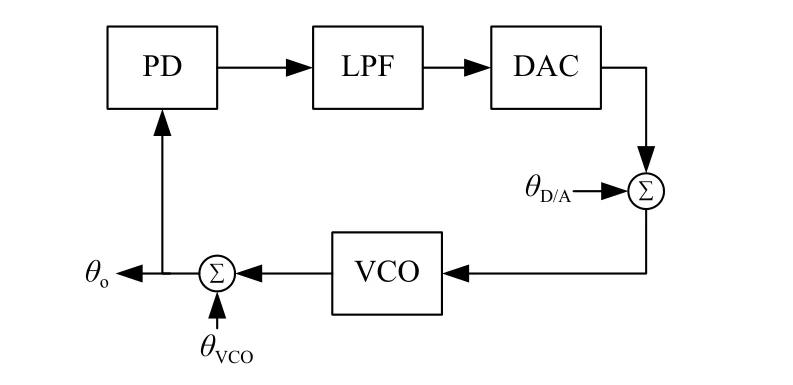
图8 等效建模前锁相环噪声传递模型

图9 等效建模后PLL噪声传递模型
根据式(16),该等效VCO噪声模型相对时间起伏的功率谱为

3 基于等效噪声模型的环路参数确定方法
通过2.1节和2.2节得到等效输入噪声和等效VCO噪声模型后,图1所示的PLL 模型被简化为无模块噪声的“理想”PLL 模型.在这个模型下,就可以直接计算两个等效噪声功率谱的交点,指导最佳环路参数的确定.
3.1 方法原理

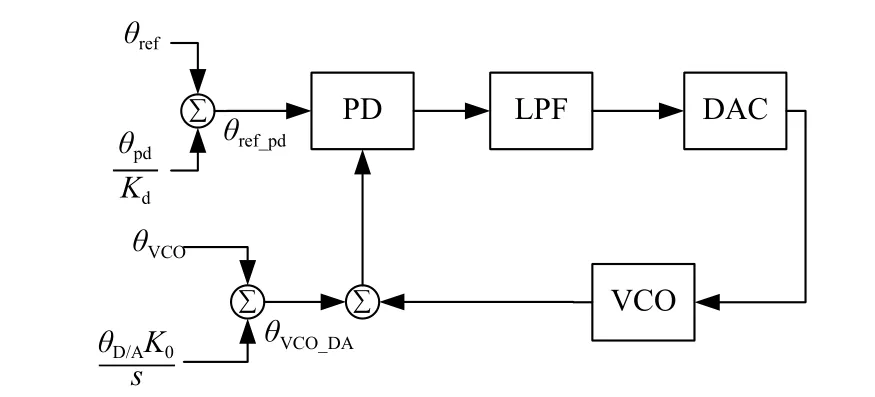
图10 基于等效噪声模型的PLL噪声传递
此时,在等效噪声模型下PLL 环路参数的设计只需要考虑等效输入噪声和等效VCO噪声.其输出噪声的功率谱为式(19),可以看到与式(8)有着相同的形式.

根据直接计算交点法的原理,计算出两个等效模型的相位噪声交点,就能得到该模型的最佳环路参数.该参数能够考虑到模块噪声对PLL 的影响,通过环路滤波作用,同时保留等效输入噪声和等效VCO噪声的低相位噪声部分,从而提高环路输出的性能.
由于等效噪声模型是基于传统PLL 的噪声传递模型建立的,因此建模前后输出的相位噪声也相同.那么等效模型的最佳环路参数同时也是传统PLL 模型的最佳环路参数.
通过式(20)直接计算两个等效噪声的功率谱交点.

在得到交点位置后就可以设置环路参数,使PLL环路传递函数与误差传递函数交点等于等效输入噪声和等效VCO噪声的功率谱交点.以一种三阶PLL为例,其环路滤波器的传递函数为


3.2 方法流程
图11为提出方法的主要步骤:
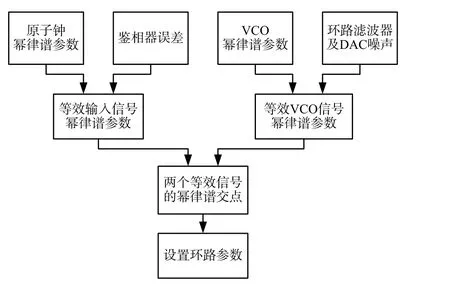
图11 等效噪声模型的数字PLL环路参数确定方法流程图
1)拟合原子钟和VCO的幂律谱参数,并根据实验参数计算鉴相器误差、环路滤波器和DAC噪声的功率谱;
2)利用幂律谱模型和式(13)与式(18)计算等效输入噪声模型和等效VCO噪声模型;
3)根据式(20)计算两个等效噪声模型的功率谱交点;
4)合理设置环路参数,使得等效噪声模型的功率谱交点与PLL传递函数交点相等.
4 实验验证及结果分析
4.1 实验条件
使用文献[9]的方法模拟一台铯钟与VCO的数据,其单边带相位噪声与频率稳定度如图12和图13所示.

图12 输入和VCO信号的单边带相位噪声

图13 输入和VCO 信号的频率稳定度
PLL 参数如表1所示.

表1 实验参数
4.2 实验结果与分析
图14为PLL 各模块噪声经过本文提出的方法处理后,得到的等效输入信号和等效VCO信号相位噪声的功率谱.与图12对比可以看到鉴相器噪声导致了明显的等效输入噪声的恶化,而由于DAC分辨率较高,等效VCO噪声的变化不大.两个噪声功率谱的交点位置为0.44 Hz.对PLL 的参数K进行修正,图15为修正后输出的频率稳定度.

图14 等效噪声模型的单边带相位噪声

图15 等效噪声模型的频率稳定度
4.2.1不同参数的性能比较
由于环路相对于等效输入噪声是LPF,相对于等效VCO噪声是高通滤波器,根据3.1节,将K设为0.44时,输出的相位噪声应该同时保留等效输入噪声和等效VCO噪声的低相位噪声特性.
与设想一致,在图16中,K=0.44时输出的相位噪声总体性能较好,同时保持着两个等效模型的低相噪特性.而随着K的增加,传递函数的交点逐渐右移,因此输出的相位噪声曲线主要以等效输入模型为主;同样K减小时输出的相位噪声曲线会以等效VCO 模型为主.

图16 不同参数下输出信号的相位噪声
图17中对比了不同参数的频率稳定度,综合来看K=0.44时输出的频率稳定度表现较好.

图17 不同参数下输出信号的频率稳定度
4.2.2与直接计算交点法的对比
图18与图19分展示了直接计算交点法与本文所提方法的对比.按照直接计算交点的方法设置环路参数K,所得到的性能曲线见图18的实线.此时通过直接计算输入和VCO的相位噪声交点所确定的K为1.39.由于没有考虑到模块噪声,在0.1 s处的频率稳定度恶化严重.虚线代表的是在本文方法指导下的输出的频率稳定度.与直接计算交点法相比,整体性能较好,没有出现较大的抬升.

图18 频率稳定度对比
图19中,按文中方法所设计的PLL的输出相位噪声曲线要比直接计算交点法好,结合了等效输入模型和等效VCO模型的低相位噪声特性.

图19 相位噪声对比
综上所述,文中提出的基于等效噪声模型的环路参数确定方法相比于传统方法有所改进.设计的PLL 的性能也较好,为PLL净化相位噪声与提高频率稳定度提供了指导.
5 总结
为了解决传统环路参数确定方法不能应用于带有模块噪声的PLL 模型,本文提出了一种新的环路参数确定的方法.先通过建立PLL 的等效噪声模型,将模块噪声等效到输入和VCO噪声中,再计算等效模型的交点设置环路参数.实验表明:文章方法得到的环路参数能使PLL 的输出总体性能较好,适用于实际应用中PLL 模型的分析,并指导环路参数的设置.接下来的工作将会对高阶PLL 进行验证,并进行实测分析.

