注重基础 化繁为简 凝炼方法 提升能力

苏明义

摘 要：2021年全国高考物理压轴题，聚焦基础知识，典型运动过程，对中学物理教学起到良好的导向作用.本文以2021年全国乙卷第25题为例，阐述如何充分发挥压轴题的教学功能，以注重基础为前提，拆分复杂问题为途径，提升学生解决物理问题的能力.

关键词：物理高考;压轴题;复杂问题拆分;能力提升

中图分类号：G633.7     文献标识码：B     文章编号：1008-4134（2021）15-0055-04

作者简介：苏明义（1962-），男，北京人，中学正高级教师，中学特级教师，研究方向：高考改革和新课程改革、理科综合能力测试的命题指导思想、原则、技术、评价研究.

高考的压轴题在高中教学与复习过程中一直倍受关注，它在某种程度上引导高中物理教学向纵深发展的方向，这一点在实际中是毋容置疑的.近年来高考压轴题大多突出对基本物理过程、典型物理状态的准确把握和综合应用，尽管试题有足够的难度，但所涉及到的知识都是主干的基础知识，所涉及到的过程和状态，都是物理学中最基本、最典型的内容，而不是一些偏、怪的情景，这样的题对中学物理教学，特别是习题教学起到了良好的导向作用.

在面对高考压轴的难题时，我们的教学是直指难题本身，还是注重对基础知识、典型过程和状态的分析，这是一个必须思考清楚的问题.如果我们直接将目光聚焦到这些压轴题上，那么会因为对于一些基础知识理解不深刻、典型物理过程（或状态）分析不清楚，在能力提升方面事倍功半.本文以2021年全国乙卷第25题为例，阐述基础知识、基本过程对解决综合难题的重要性，以及应如何充分发挥这种压轴题的教学功能，以注重基础为前提，以拆分复杂问题为途径，提升学生解决物理问题的能力.

1 原题呈现

（2021年全国乙卷 25题）如图1所示，一倾角为α的光滑固定斜面的顶端放有质量M=0.06kg的U型导体框，导体框的电阻忽略不计;一电阻R=3Ω的金属棒CD的两端置于导体框上，与导体框构成矩形回路CDEF;EF与斜面底边平行，长度L=0.6m.初始时CD与EF相距s0=0.4m，金属棒与导体框同时由静止开始下滑，金属棒下滑距离s1=316m后进入一方向垂直于斜面的匀强磁场区域，磁场边界（图中虚线）与斜面底边平行;金属棒在磁场中做匀速运动，直至离开磁场区域.当金属棒离开磁场的瞬间，导体框的EF边正好进入磁场，并在匀速运动一段距离后开始加速.已知金属棒与导体框之间始终接触良好，磁场的磁感应强度大小B=1T，重力加速度大小取g=10m/s2，sinα=0.6.求：

（1）金属棒在磁场中运动时所受安培力的大小;

（2）金属棒的质量以及金属棒与导体框之间的动摩擦因数;

（3）导体框匀速运动的距离.

分析：本题是电磁感应与力学的综合题，涉及到了运动学、牛顿运动定律、电磁感应、欧姆定律、安培力等主干知识，以及学生熟悉的匀加速直线运动、匀速运动、导体匀速切割磁感线等物理过程.但由于问题的情景涉及到两个研究对象和多个物理过程，且摩擦力是否存在以及方向的分析又比较隐蔽，加之金属棒质量、棒与框之间的动摩擦因数未知，导致滑动摩擦力大小与运动状态的变化二者的分析相互制约，这些都增大了分析解答的难度.如何充分发挥此类试题的教学功能，有效地提升学生的学科关键能力呢？

2 化繁為简、拆分设问举例

如果将原题直接用于教学或一轮复习之中，对于很多学生来说显然是很难消化的，即使是勉强听懂了也很难达到“会”的水平，很难达到掌握方法的程度.笔者认为，对于这样的复杂问题，在教学中应结合学生的能力水平进行适当的拆分，将复杂问题化繁为简，把拆分出的“小问题”逐一解决，引导学生对典型的物理过程或状态进行准确的分析，从而达到培养能力的目的.

我们可以将问题进行展开，沿着解决问题的思路“沿途设问”，有些问题是沿着物理过程进行拆分，有些问题是沿着问题的结构进行拆分.意图是以问题为导向，引导学生的思维向最终解决问题的方向进发.

（1）试分析说明U型导体框和金属棒由静止开始能否一起沿斜面下滑，框与棒间的摩擦力大小f1.

答：一起沿斜面下滑，f1=0.

当然，为了充分挖掘本题的教学价值，我们还可以在此基础上，再深挖出一些问题来，如求解棒在磁场中匀速运动过程中产生的焦耳热，以及摩擦所产生的热;磁场区域的宽度x;棒与框共速后，棒的加速度大小a4;棒与框共速后，框的运动性质分析;整个过程中棒和框的v-t图像……

3 化繁为简的拆分，助力凝炼思路方法

拆分的目的是要在逐一的“小问题”上加深对知识和物理过程的理解，在这些问题各个击破的过程中体会分析的思路、凝炼方法，所以在拆分过程中要注意以下几个问题.

3.1 把握好问题拆分的“度”

通过问题的拆分可以化繁为简，从而有效地降低问题的思维难度，便于学生解决问题.但并不是拆分得越细越好.就像泰山陡峭不便攀登需要修台阶一样，台阶修得过大攀登仍然困难，若台阶修得过小，也同样不利于攀登.所以这种拆分教师要根据所教学生的能力水平而定，使得拆分出的每个问题都能让学生通过努力得到解决，同时又能从中体会到隐含的思路方法.

3.2 形象化物理过程

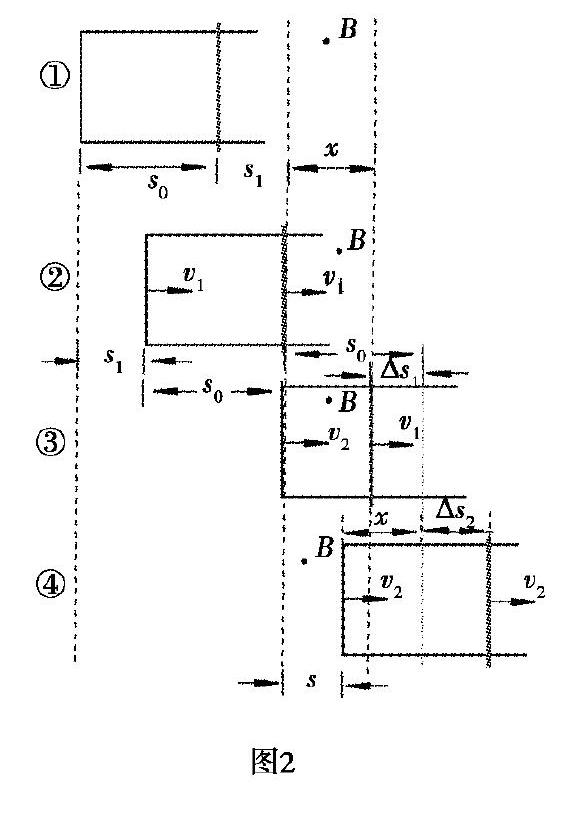
上述拆分的问题是老师事先深思熟虑的结果，在将这些问题呈现给学生时，学生是否能与教师同步反应出这些物理过程或状态呢，这是我们在教学中必须要考虑的现实问题.如果学生头脑中没有这种物理图景，那么这样的讲析可能就是教师的“一言堂”“独角戏”.为了充分调动学生的思维活动，可以画出（或让学生画出）如图2所示的过程草图，以将复杂、抽象的物理过程形象化.

3.3 战略上的总体布局

在教学中这样抓住典型物理过程的拆分，并不是到高考复习的最后阶段才进行，应该在日常的教学过程中做好战略上的准备，要对高中教学有一个整体的布局.

如在力学的教学过程中，可以先从水平面上的板块模型的相互作用开始积累.如图3所示，木板A在水平面上减速滑行，当速度为v0时将物块B轻放在板的右端.

再到沿斜面下滑的板块模型：如图4所示，在倾角为α的光滑斜面上的木板B上叠放有物块A，由静止释放，当B运动到C点时受到沿斜面向上的拉力F的作用使其匀速下滑……

具体的问题内容，可以先从运动学角度分析两个运动的关系，再从运动和力的关系把握物理过程的发展方向，然后再从能量角度综合考虑位移与相互作用力的问题.这样的战略布局，才有可能到最后“力电”综合时有效地提升学生的分析综合能力.

3.4 适度综合

上述的拆分练习，只是为了找到与学生思维水平相匹配的切入点，并以此来引导学生体会分析解决问题的思路方法，但我们也必须清醒地认识到，这样一个一个的个体问题的解决与简单的叠加，决不等于学生分析综合能力的形成.因此，在个体问题练习的基础上，还要适时地进行适度的综合训练，将“沿途设问”的台阶撤掉，让学生自主搭建思维台阶，只有这样，才能将能力的提升落到实处.

4 抓住基础、梳理方法、提升能力

学生头脑中累积丰富、准确的物理过程图景，这是将复杂问题进行拆分的基础，同时这样将复杂问题的拆分训练，又有利于加深对基础知识的理解和物理图景的精准把握.因此，要充分考虑到将复杂问题进行适当的拆分，夯实基础，落实方法，提升能力，树立学习自信心.

4.1 为学生走向成功搭建台阶

对一个复杂问题进行拆分，采用沿着解决问题的思路“沿途设问”的方式进行“一题多问”，降低问题的思维梯度，从而使拆分后的每一个问题都能处于学生“跳一跳，够得着”的状态，使学生在解决每一个小问题时，既能面对挑战，又能通过努力获得成功的体验.因此，既可以有效地培养能力，又提升了学生克服困难的信心.

4.2 有利于对典型物理过程或状态的理解与积累

通过对问题的拆分，可以在一些学生容易忽略的点上设计问题，引导学生对每个物理过程发生的条件、发展的规律都能作出逻辑的分析与判断，特别是对物理过程发展有多种可能性的问题，通过设计相应的问题，促进学生能辩得清、说得明、理得顺.如对于板块模型从有相对滑动到共速后它们之间的摩擦力的方向问题，以及能否保持住共速的过程等.这样的处理，以“小问题”辨析，不仅可以丰富学生头脑中物理过程和状态的图景，还可以促进这些物理图像的精準化，从而为解决复杂问题奠定基础.

4.3 感受与体验解决复杂问题的思路方法

通过“沿途设问”多个简单问题的逐一解决，可以使学生体会到综合难题往往是多个简单问题在叠加，因而使得解决问题的路径“显性化”，有利于学生体会到解决复杂问题的思维路径，同时也为学生模仿分析复杂问题的思路方法提供了范例.因此这是引导学生凝炼思路方法的有效手段，是培养学生分析综合能力的具体过程.

总之，高考压轴题通常会成为物理习题中的经典之作，因此引起教师在教学中的充分重视是正常的，但我们不应只关注这些题的考点和解法，更应该在教学中冷静地分析这些试题的教学价值，要从学生的认知规律出发，要从学生的实际能力水平出发，最大限度地发挥这些经典试题的教学功能.

（收稿日期：2021-06-20）