不同版本的GAMIT超短基线数据解算精度分析
何月帆,聂桂根,2,武曙光,李海洋
(1. 武汉大学 卫星导航定位技术研究中心,湖北 武汉 430079;2. 地球空间信息技术协同创新中心,湖北 武汉 430079)
GAMIT软件是美国麻省理工学院(Massachusetts Institute of Technology,MIT)与斯克里普斯海洋研究所(Scripps Institution of Oceanography,SIO)共同研制的高精度数据后处理软件,由于其优良的解算特性,在GNSS数据高精度解算领域得到广泛应用[1]。但是由于北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)与GPS系统在星座结构、坐标框架、时间系统、信号频率等方面都有着明显的差异,故在GAMIT10.6版本之前只能解算GPS数据,对其他GNSS系统数据不能进行有效处理[2]。GAMIT10.61版本开始陆续可以处理GNSS多系统观测数据,此版本发布于2017年7月,其特点是不仅能处理GPS数据,还能够单独处理如北斗(BDS)、伽利略(GALILEO)、印度区域卫星导航系统(IRNSS)的观测数据[3]。随着GNSS误差模型的不断精化,基于GAMIT进行的基线解算也逐步增加了最新的GNSS误差改正模型,如参考框架IGS14和ITRF2014、对流层映射函数GMF/VMF、大气负载、非潮汐大气负载等[4]。GAMIT软件的用途极为广泛,其中一个重要作用就是用来分析测站的坐标和速度,进而对建筑物进行动态或静态的形变分析,GAMIT主要输出的是松弛约束解、参数估值及其协方差(矩阵)的h文件[5]。通过此文件能够传递给GLOBK软件包,以进行数据解算来求解测站位置和速度。除此之外,GAMIT可以应用于地球动力学、地壳形变、气象水汽等领域的科学研究[6]。
现如今GAMIT软件得到广泛的应用,新版本软件也得到定期的更新。目前使用比较广泛的GAMIT软件版本有10.5、10.6、10.61和最新的10.7,而各版本软件之间也有一些模型改正方面的差异。已有研究对各版本之间解算差异的比较还很少,因此文中选用GAMIT10.5、GAMIT10.6、GAMIT10.61、GAMIT10.7这4个不同版本的软件,对北京某一地区所测的超短基线场的5个GPS点及其周边的陆态网的站点进行联测处理,比较不同版本在解算成果上的差异,分析造成这些差异的因素。
1 GPS资料概况
该超短基线场由5个点组成,网形为等腰梯形,各条基线的夹角约为60°,长度约为6 m,每次同步校准最多5台GNSS接收机。该校准场基准点选择高度角在15°以上,天空无障碍物,地质构造坚固稳定且远离电磁信号干扰源和易于产生多路径信号源的地方,如图1所示:文中采用Trimble Net R9接收机,对这5个点连续进行为期3 d的静态观测,观测时间为2019年11月5日至7日,采样频率15 s,天线型号为TRM55971。
参考站选取的是中国境内和周边的6个IGS站点(见图2),包括POL2、BADG、YSSK、LHAZ、TWTF和SUWN,以及北京市及周边均匀分布的5个CMONOC站点。这些参考站均匀分布在超短基线场所在地周围,使得组成的GPS网有较好的网形和精度。本次处理使用的各IGS站的观测文件、广播星历、精密星历以及精密钟差均从美国国家航空航天局(National Aeronautics and Space Administration,NASA) 全球数据中心SOPAC下载得到;其中5个CMONOC参考站数据来自陆态网数据中心教育部数据子系统服务器。
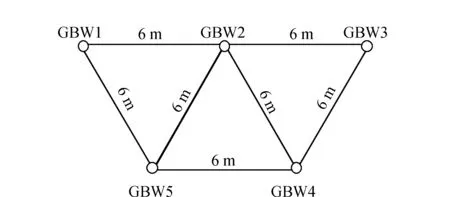
图1 网形设计

图2 GAMIT处理使用的IGS站分布
2 GAMIT设计方案
本文采用的数据处理软件由GAMIT10.5、GAMIT10.6、GAMIT10.61、GAMIT10.7所组成。如表1所示,文中对这些不同版本的GAMIT软件进行了简单的比较说明。首先使用GAMIT计算2019年11月5日至7日的单日基线结果,再利用GLOBK进行整体平差得各站坐标。

表1 不同版本的GAMIT软件比较
主要的GAMIT基线解算策略包括:
1)解算类型为BASELINE,将卫星轨道参数固定;
2)观测值类型为双差观测值;
3)截止高度角设置为15°,以减少多路径效应等与卫星高度角有关的误差源的影响;
4)测站约束为松弛约束,IGS站点N,E方向10 cm,U方向20 cm;待估测站N,E,U方向皆为30 m;
5)天线相位中心改正模型为AZEL,将天线相位中心看成是卫星高度角和方位角的函数,采用双线性插值;
6)对流层延迟改正:映射函数采用VMF1;每2 h估计一次天顶对流层延迟参数;每12 h估计一次大气水平梯度参数;
7)电离层延迟改正:采用LC组合观测值消除一阶电离层延迟的影响,高阶电离层延迟模型为GMAP;
7)地磁场参考模型为IGRF11;
8)潮汐改正:采用的潮汐改正项包括地球固体潮(IERS2003)、极潮、海潮(FES2004)以及大气潮(全球格网模型ANU100826);非潮汐改正:非潮汐大气模型改正(atmfilt_cm.year模型);
9)参考框架:ITRF2014。
文中采用分级两步法进行基线解算和网平差,即首先将IGS站、CMONOC参考站共11个站点作为框架网(见图3),经过基线解算与网平差,得出CMONOC参考站的ITRF2014框架下的精确坐标。然后将CMONOC参考站、项目测站作为下一级子网,采用相同的数据处理策略得出5个项目测站的基线解算与坐标结果。

图3 GAMIT处理使用的CMONOC参考站分布
3 结果分析与比较
3.1 基线解算
GAMIT基线解算完成后,可将基线解的标准均方根误差(Normalized Root Mean Square, NRMS)作为GPS同步环质量好坏的一个指标,表示单时段解算的基线值偏离其加权平均值Y的程度[7],其定义如式(1)所示。通常要求NRMS值小于0.3 cm,若大于0.5 cm,则表示基线处理过程中周跳可能未得到完全修复[8-9]。
(1)
表2为利用这4款不同版本的GAMIT软件进行基线解算获得的年积日309—311单日解的NRMS值。

表2 GAMIT解算获得的NRMS值表 cm
从表2可以看出,除了GAMIT10.61以外,其他版本的GAMIT基线解算结果的NRMS值均在0.3以内,产生这种结果的原因可能是GAMIT10.61软件在处理基线时,其周跳模糊度模型未完善所致。
另外,也可以通过检查所有站点是否全部参与基线解算来检查解算效果。在单日解文件中的总结文件中,若是Number of stations used(使用的测站数目)与Total xfiles(生成的X文件的数量)一致,则说明全部站点参与了基线解算[10]。经检查,本次解算所有测站均参与解算。
在基线解算的质量控制中,还可以采用其重复性来作为其更高等级的质量控制指标。重复性的定义为:
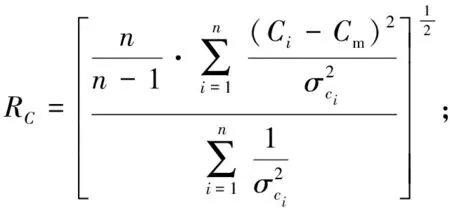
(2)

从表3可以看出,在水平以及长度分量上,其基线重复率均在亚毫米级,而在垂直分量上,其内符
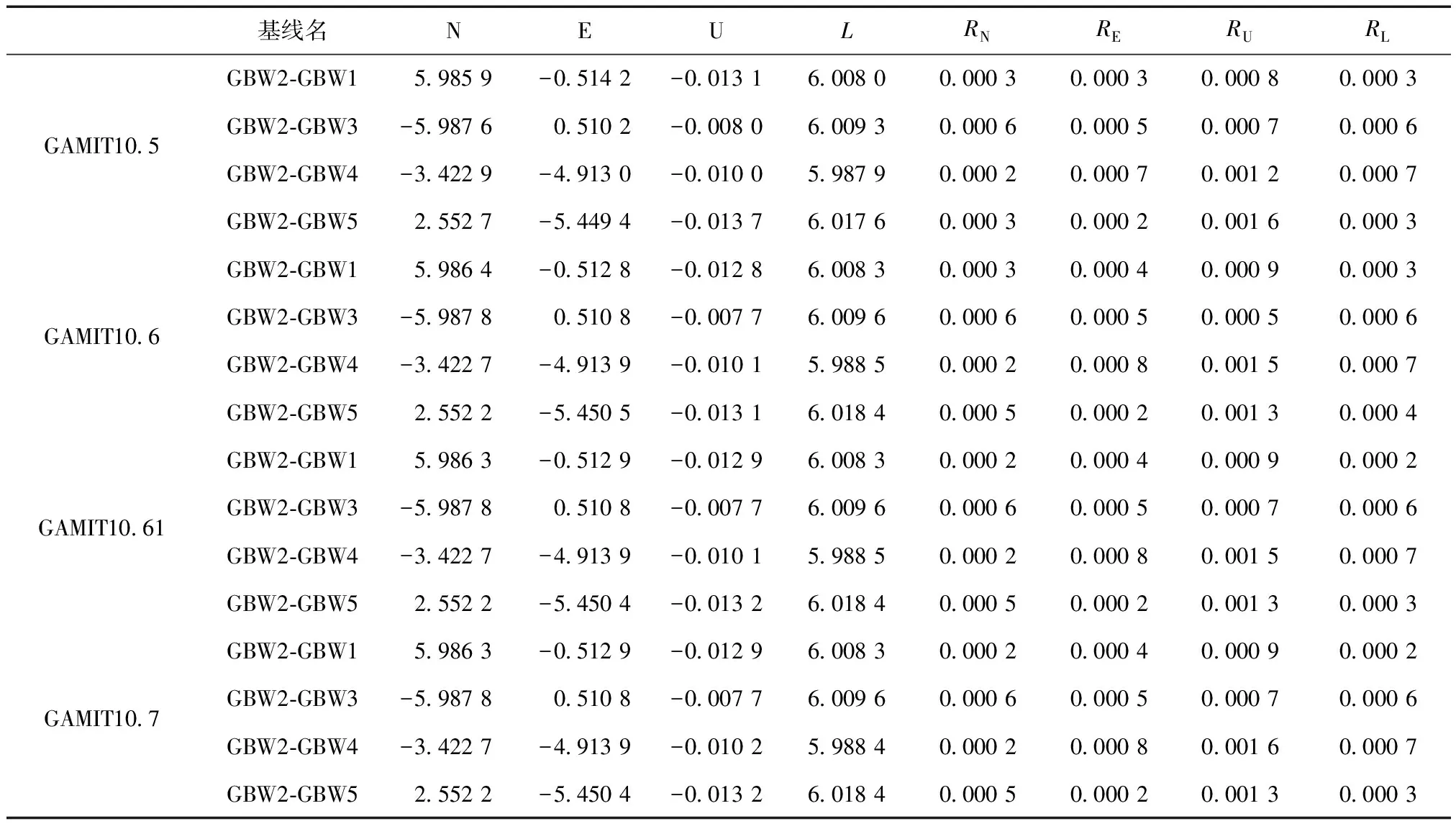
表3 N,E,U分量及长度方向的基线重复率 m
合精度稍差,有少量基线重复率可达到毫米级。故从基线分量重复率结果来看,这4款不同版本的GAMIT软件均满足基线解算精度要求。
全站仪测边结果列于表4。可以看出,若以全站仪两日实测值的均值作为基准,则4个版本的基线结果最大差异均不到3 mm,解算成果均符合精度要求。

表4 全站仪实测基线边长与对应的GAMIT基线解算结果 m
3.2 GLOBK网平差
基线解算完成以后,使用所获得的H文件作为观测量进行GLOBK网平差,起算点坐标约束在N,E,U 3个坐标分量为1 cm,1 cm,2 cm。各个版本的GAMIT/GLOBK软件所得出的坐标结果如表5所示。

表5 测站点位坐标结果(ITRF, 2019.848)
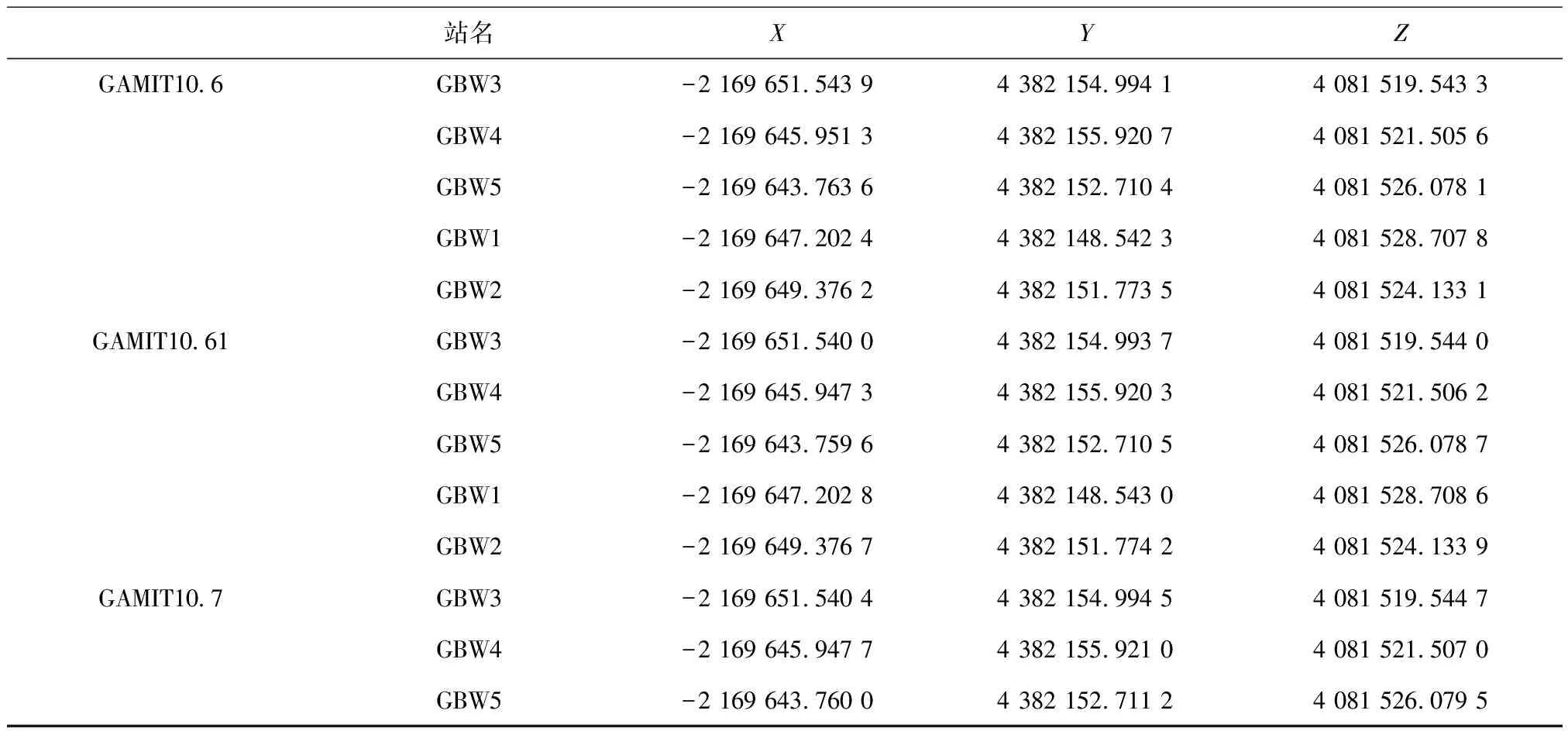
续表5
由表5所列出的坐标结果,然后取这4款软件的坐标结果的平均值作为虚拟的真值,分别求出这4种方案下各个项目测站的坐标与其虚拟真值间的距离,以此来对比它们坐标结果的稳健度,如图4—图6所示。
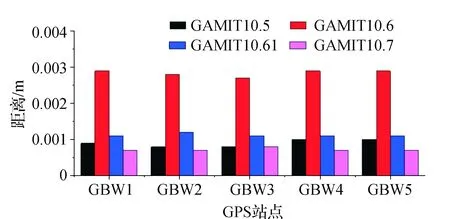
图4 X方向点位坐标与均值间的距离

图5 Y方向点位坐标与均值间的距离

图6 Z方向点位坐标与均值间的距离
如图4—图6所示,用同一解算方案,利用不同版本的GAMIT/GLOBK软件进行基线解算和网平差处理,所得到的坐标结果会有细微的差距,与其均值间的差异均不超过1 cm,对比4款软件可以看出,不管在水平分量还是在垂直分量上,最新版本GAMIT10.7软件与均值的差异最小,坐标稳健性最好,均不到2 mm;其次是GAMIT10.61版本;GAMIT10.6和GAMIT10.5版本相比较而言与均值差异较大,最大可达4.6 mm。
4 结 论
文中采用4种不同版本的GAMIT软件对新建立的GPS超短基线场进行GAMIT/GLOBK高精度数据处理,通过对基线解算后NRMS值、基线重复性、独立基线长度比较以及网平差后点位坐标稳健性等方面的对比分析,可以看出GAMIT在进行GPS超短基线处理时,其GAMIT10.7版本的解算结果最好,而GAMIT10.61除NRMS值较大以外,其他处理结果相比于GAMIT10.6和GAMIT10.5来讲较好。文中通过对比不同GAMIT版本在数据解算中的精度和坐标结果的可靠性,对于类似的数据处理解算具有一定的参考意义。同时随着多系统卫星接收机的普及,对于该类接收机的校准工作需要综合处理多系统数据,这将是本文下一步的研究计划。

