机载激光点云中电力线的自动提取与重建
程宇航,白征东,辛浩浩,张 强,郭锦萍
(清华大学 土木工程系,北京 100084)
随着我国国民经济快速发展,电力网络规模不断扩大,高效、有序地对电力网络进行管理并保证其正常运行成为电力系统建设中的重要问题[1]。输电线路作为电力网络的主要组成部分,可以将电能输送至全国各地,发挥着至关重要的作用[2-3]。机载激光雷达系统以无人机为载体,以激光脉冲为测量媒介,可以同时采集测量区域的高精度点云数据和高分辨率图像,具有测量速度快、精度高、全数字特征等特点,在输电线路测量中得到广泛应用[4-6]。
利用机载激光雷达系统进行输电线路测量可以获取海量的点云数据,快速、准确地实现输电线路走廊点云中电力线点云数据的分割提取与三维重建,直接关系到此技术在输电线路测量中的应用价值,因此有必要研究一种高效精准的电力线点云提取与重建方法。目前,国内外关于电力线点云自动提取的研究通常是利用基于高程和密度的提取算法进行电力线候选点集的提取,利用K-means聚类算法以及Hough Transform算法实现单根电力线的提取。
基于高程和密度的提取算法是利用输电线路走廊中电力线与其他元素在高程和密度上的差异来实现电力线点云的提取[7-11],对输电线路点云空间进行栅格化处理,通过计算每个栅格内的点云高程特征和密度特征,再与经验阈值或是动态阈值[11](可以根据数据特征自适应地调整阈值大小)比较来判断栅格内点云为电力线或非电力线,最终实现电力线点云自动提取。此方法简单高效,提取速度快,但对于复杂地形电力线点云容易出现错误提取的问题,不利于工程应用。
K-means聚类算法是一种迭代求解的聚类分析方法,通过对电力线点云的投影点进行聚类分析,实现电力线点云的自动提取[12-15]。投影时将电力线点云投影到相应电力线的切平面(该平面垂直于电力线),使用K-means聚类方法进行投影点的聚类,通过聚类中心进行类别的传递和规则化。为了提高K-means算法的聚类精度和收敛速度,可以在种子点的选取过程中增加约束条件,例如导线的间距等[12]。此种方法具有很好的提取精度,但反复迭代计算会占用大量计算机内存,提取效率不高。
Hough Transform算法是一种广泛应用于计算机视觉领域的特征提取算法,通过电力线点云水平投影的直线提取来实现电力线点云的自动提取[8,11,16-17]。对点坐标与直线方程参数进行转换,将提取直线的问题转换为寻找直线交点的问题,再通过一定的阈值判断,提取出电力线点云。由于Hough Transform算法在直线提取上的优越性,此方法对于结构清晰的电力线点云具有很好的提取效果,但对于复杂地形下的电力线点云提取效果不佳。
除此之外,Xinyan等[18]提出了一种基于点集协方差矩阵特征值的电力线提取方法。首先,对输电线路点云进行栅格化处理,计算栅格内点集协方差矩阵的特征值,通过比较特征值的大小提取出线性结构,实现电力线点云的粗提取;再利用Hough Transform算法和K-means聚类算法实现单根电力线的分割提取。Matti等[19]将主成分分析方法和RANSAC算法引入到电力线提取中,该算法首先对栅格化后的点集进行主成分分析,得到电力线候选点集;再利用RANSAC算法搜索和近邻点连续搜索,提取出单根电力线。但此两种方法中的基于协方差矩阵特征值与主成分分析的方法都对数据中的噪声比较敏感,容易出现错误提取,抗差性不强。
鉴于此,文中从输电线路激光点云数据特征出发,提出一种基于栅格化空间分布特征的算法进行电力线候选点集的提取,再利用K-means聚类算法和随机抽样一致性算法(Random Sample Consensus,RANSAC)实现单根电力线的提取与重建,重点实现电力线候选点集的快速、准确提取,为机载激光雷达海量点云数据的处理提供参考。
1 电力线点云自动提取与重建问题描述
1.1 输电线路机载激光点云特征
由机载激光雷达系统扫描作业方式可知,采集到的输电线路点云数据主要包含电力线点云、杆塔点云和地物点云3类,如图1所示。电力线候选点集的自动提取是实现电力线自动提取与重建的必要环节,因此需要对3种类别点云在空间分布与结构上的特征进行分析。

图1 输电线路走廊机载激光点云数据
1)电力线点云。高程方面,由于要保证输电线路高压传输的安全性问题,电力线一般通过杆塔架设在半空中,距离地物有一定安全距离,因此电力线点云的平均高程要显著大于地物点云的高程;密度方面,局部范围内电力线点云的密度要显著小于杆塔和地物点云的密度;结构方面,电力线点云垂直投影近似于一条曲线,水平投影近似于一条直线。
2)杆塔点云。高程方面,杆塔点云的高程分布更为全面和连续,覆盖了从低到高的高程值;密度方面,杆塔部分点云在水平投影面上的密度要显著大于其余部分;结构方面,杆塔点云多为直线、平面组合结构,具有明显的几何特征。
3)地物点云。平坦地形下的地物点云的高程值显著低于电力线与杆塔点云,且在很小的范围内变化;复杂地形下的地物点云分布较为随机混乱,在空间分布与结构上均不具有明显特征。
1.2 电力线三维数学模型
电力线三维重建的一个关键环节是电力线三维数学模型的选取,不同的数学模型会直接影响电力线重建精度。由于电力线点云在空间结构上的特征,电力线三维数学模型可以分为XOY水平面投影模型和某垂直投影面(XOZ平面或YOZ平面)的投影模型。水平投影面上一般采用直线模型,垂直投影面上采用的模型主要有抛物线模型和悬链线模型两种[20]。
文中将分别采用抛物线模型、悬链线模型与直线模型的两种组合对电力线进行重建,在垂直投影面上,两种模型均需考虑电力线点云的坐标在X轴方向和Y轴方向的取值范围xrange,yrange,两者的计算公式为:
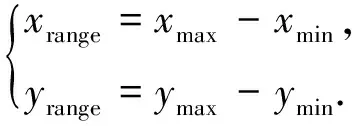
(1)
式中:xmax,xmin分别为电力线点云的x坐标的最大值、最小值;ymax,ymin分别为电力线点云的y坐标的最大值、最小值。
抛物线模型、悬链线模型与直线模型的两种组合数学表达式为:

(2)
式中:k,b是直线模型参数;a0,a1,a2是抛物线模型参数。
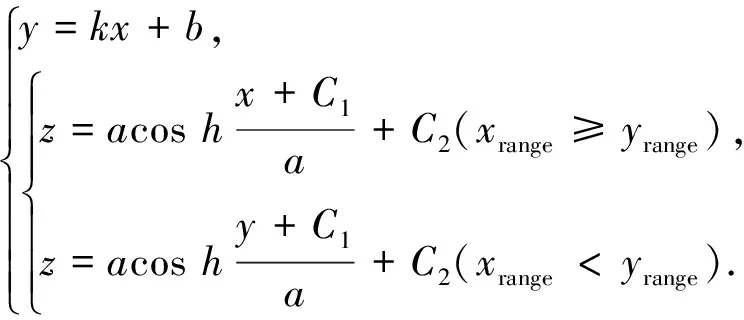
(3)
式中:k,b是直线模型参数,a,C1,C2为悬链线模型参数。图2为悬链线模型参数具体示意图(以XOZ投影面为例)。
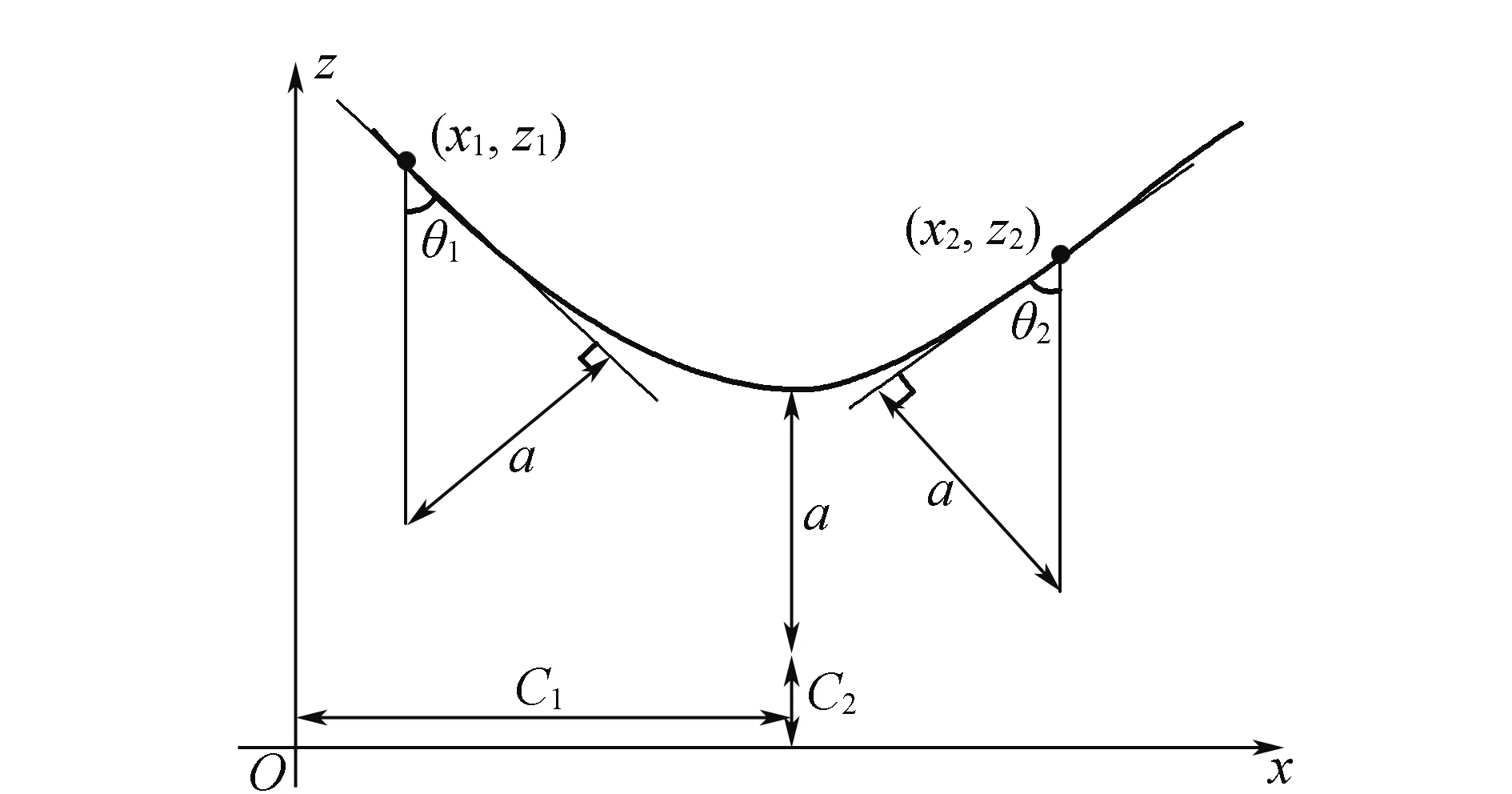
图2 悬链线模型参数示意图
2 电力线自动提取与重建算法
为了有效提高当前电力线自动提取算法的精度与效率,文中根据输电线路激光点云数据的空间分布与结构特征,提出一种基于栅格化空间分布特征的算法进行电力线候选点集的提取,再利用K-means聚类算法和RANSAC搜索算法实现单根电力线的提取与重建。
2.1 电力线候选点集自动提取
电力线候选点集的提取是后续单根电力线自动提取与重建的重要环节,文中在传统高程与密度阈值提取算法的基础上,提出并采用一种基于栅格化密度阈值与拟合残差阈值的电力线候选点集自动提取算法,算法工作原理如下:
1)求出输电线路原始点云数据的边界值,确定初始点云分布空间S0:
(4)
式中:(x,y,z)为任意一点的空间三维坐标值。
2)根据输电线路点云数据的尺度和数据质量,选取合适的栅格化尺度dx,dz(以XOZ投影面为例),将初始点云分布空间S0沿X轴方向和Z轴方向划分为m×n个子空间,如式(5)所示。
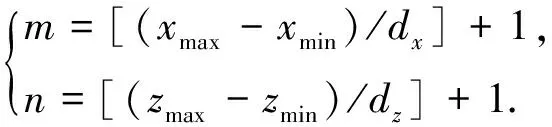
(5)
其中,[(xmax-xmin)/dx]与[(zmax-zmin)/dz]表示求取不大于(xmax-xmin)/dx,(zmax-zmin)/dz的最大整数。
3)统计每个子空间Si,j内的点云数量值Ni,j及其占周围8个子空间及其自身内的点云数量总和的比例pi,j,将Ni,j与pi,j作为子空间Si,j的特征值,如式(6)和图3所示。
(6)
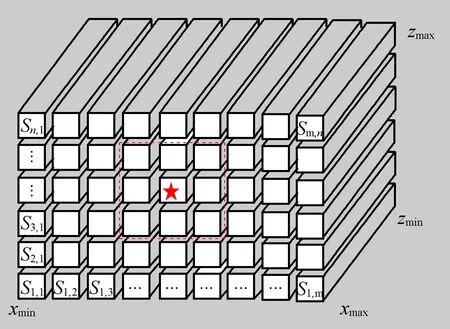
图3 子空间特征值计算示意图
4)设置临界阈值δN和δp,并依据特征值对子空间进行归类:当子空间Si,j的特征值满足Ni,j≤δN和pi,j≥δp,则认为该子空间为1类子空间;反之,认为该子空间为2类子空间。2类子空间内的点云可认为是非电力线点云;1类子空间内的点云仍含有少量非电力线点云与电力线点云,需要进一步通过拟合残差分析进行提取。
5)对1类子空间中点云进行曲线拟合,拟合模型采用直线模型与抛物线模型的组合,如式(2)所示,并计算出每个点的拟合残差。
(7)
式中:vx,vz分别表示X方向和Z方向上的拟合残差分量。
6)设置临界阈值δv,依据拟合残差大小对每个点进行归类:当一个点的拟合残差满足v≤δv,则认为该点为电力线候选点;反之,则是非电力线点云。临界阈值δv可表示为:
δv=μv+λσv.
(8)
式中:μv,σv分别表示拟合残差v的平均值和标准差;λ为标准差系数。图4给出了基于栅格化密度阈值与拟合残差阈值的电力线候选点集自动提取的算法流程。

图4 电力线候选点集自动提取算法流程
2.2 电力线提取与重建
实现电力线的自动提取是电力线三维重建的前提,电力线分为单根导线和分裂导线。根据输电线路电力线的空间特征,各电力线近似于一组平行线,且导线间距一般为10~20 m,各分裂子导线间距一般为0.2~0.5 m。根据电力线在空间分布上的特点,文中采用双重K-means算法实现电力线的自动提取,算法工作原理如下:
1)对电力线候选点集采用抛物线模型与直线模型组合进行拟合,计算出每个点的拟合残差值v。
2)将分裂导线当作一根导线,采用K-means算法对拟合残差进行聚类,输入聚类数目K、种子点间距D等参数。
3)随机选择K个种子点,不断迭代直至种子点集合不再变化,实现单根导线之间的相互分离,得到每根导线的点云。
4)对单根分裂导线进行拟合,计算出每个点的拟合残差v′,同样采用K-means算法对拟合残差进行聚类,实现分裂子导线之间的相互分裂,得到每根子导线的点云。
电力线三维重建是指将提取得到的单根电力线点云进行精确矢量化。考虑到电力线点云中还存在着一定噪声点,最小二乘拟合无法消除这些噪声点的影响,拟合误差较大,文中采用RANSAC算法实现电力线三维重建。RANSAC算法随机选取数据得到模型拟合参数,通过反复迭代得到最优的模型参数,可以消除噪声点的干扰,RANSAC算法流程如图5所示。
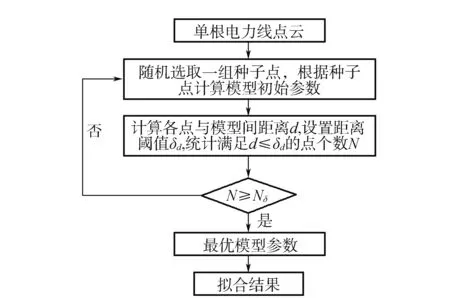
图5 RANSAC算法流程
3 试验验证与分析
为验证文中所提出的电力线自动提取与重建算法的有效性,并对电力线候选点集提取算法的效率及两种电力线数学模型的拟合效果进行分析,文中采用机载激光雷达实测的输电线路走廊点云数据作为试验数据,试验平台的配置为Intel八核3.6 GHz CPU、64 GB内存,装配Windows 10系统。
3.1 试验数据
文中所采用试验数据由飞马公司的机载激光雷达系统D300L获取,搭载Rigel mini VUX-1UAV激光雷达系统,最远测量距离为250 m、水平分辨率为0.05°~0.5°、点位精度为5 cm 。图6为获取到的4组单档输电线路点云数据,分裂导线均为二分裂,4组试验数据概况见表1,各组试验数据在点云体量、地形条件上存在一定差异。
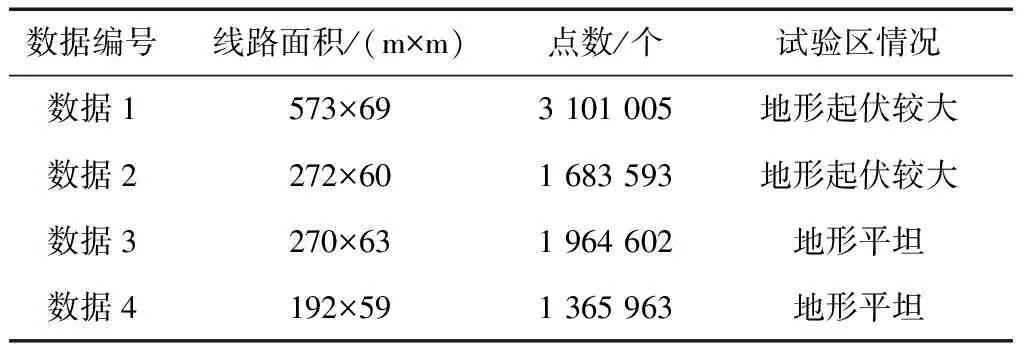
表1 试验数据概况
3.2 试验结果与分析
采用文中所提出的基于栅格化密度阈值与拟合残差阈值的电力线候选点集自动提取算法,对4组试验数据进行电力线候选点集自动提取,并统计各组数据的算法处理时间以及提取得到的点个数。综合考虑4组试验数据的基本信息,算法中的栅格化尺度dx和dz均取5 m;临界阈值δN和δp分别取300和0.5;拟合残差阈值δv的标准差系数λ取值为2.5,对应于1.24%的剔除率。提取结果如图6所示,其中蓝色点为1类子空间中的非电力线点,红色点为最终提取结果。
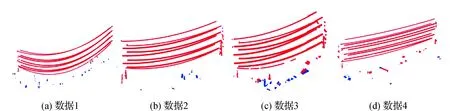
图6 电力线候选点集提取
为了进一步分析算法的提取效率,同时利用传统的电力线自动提取算法[10-11]进行电力线候选点集提取,然后对提取的电力线点云进行人工复核,人工删除非电力线候选点,统计留下的电力线候选点个数。将人工提取的点个数与算法提取的点个数之比作为算法提取电力线候选点的正确率,统计结果如表2所示。

表2 电力线候选点集提取结果
由表2可知,文中所提出的电力线候选点集提取算法对4组试验数据的提取正确率均在97%以上,且优于传统电力线自动提取算法,达到了很好的提取效果。但也可看出算法提取的点云数都比人工提取点云数大,这是因为电力线点云附近存在着少量的噪声点,具有与电力线点云相似的空间分布与结构特征,需要在后续电力线提取与重建中消除这些噪声点的影响。
由试验数据的基本信息可知,4组试验数据均包含单根导线和二分裂导线。采用双重K-means算法对4组经提取得到的电力线候选点集进行电力线提取与重建,以第一组试验数据为例,提取与重建结果如图7所示。结果表明,双重K-means算法能够准确地对单根导线、分裂子导线进行提取与重建。
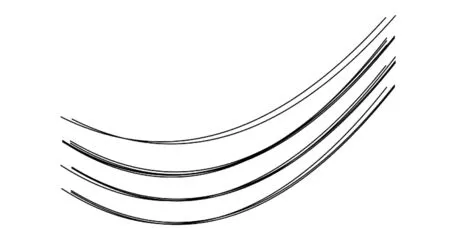
图7 电力线提取与重建
综上所述,通过试验证明了本文提出的电力线提取与重建方法的可行性,具有较高的电力线候选点集提取正确率,电力线的提取与重建效果较好。
4 结束语
文中针对传统电力线点云自动提取方法在抗差性、准确性上的不足,在分析传统特征提取方法的基础上,阐述了输电线路走廊上电力线、电塔、地物点云在空间特征上的差异,提出了一种新的基于激光点云的电力线自动提取与重建方法。利用4组实际输电线路点云进行了可行性试验,试验结果表明,所提方法对电力线候选点集的提取正确率均在97%以上,双重K-means算法能够准确地对电力线进行提取与重建,具有较高的提取正确率,可为实际工程的应用提供参考。

