高一学生数学学习适应性及对策

高明

摘要：高一数学是所有高中数学学习的基础。在此前提下，探究高一生数学学习不适应的具体原因，针对高一数学学习不适应的现象提供有效的补救措施，以此做到调整高一数学学习方式，转变对数学的学习态度。提高数学学习的实效性已成为当务之急。

关键词：高一数学;学生;学习适应性;对策

前言：高中数学能不能教好，高中的关鍵是第一年的基础学习。如果学生有良好的数学知识，将来学习数学会更容易。如果没有掌握好，就会导致学习数学的兴趣降低，自信心下降，影响数学的学习心理，下一步学习障碍将会更严重。

一、高一学生数学学习适应性问题

1.新人际关系引起的数学学习适应不良

在高中数学学习阶段，高中数学老师给了学生无价的信心和依赖。在高一学习结束之初，高一学生涯开始之初，学生们不再面对之前中学的老师们。当面对不知名的老师时，他们不可避免地会失去对中学老师的依赖。鉴于心理适应性，随着年龄的增长和各种原因，高一学生在适应新的和不知名的老师方面变得非常被动。另一方面，高中教师对待学生的心态也与高中教师不同。由于高一学生进入成年期，高中教师对学生的教育模式比中学教师更成熟。

2.新的同学造成的数学学习不适应

上高中后，学生已经从中学的“稚嫩”逐步转向成熟。每天站得最多的不再是他们的父母和老师，而是他们的同学。部分学生可以很快融入新的班级。它需要例如一两周或更短的时间与周围的同学建立良好的友谊。相比之下，有些学生因为个性和其他许多原因需要很多时间。适应周围的同学需要半年、一年甚至更长时间，在教室或宿舍里和同学相处都没有办法。他们总觉得自己和同学之间有隔阂。他们认为别人不会与自己接触，他们总是隐藏一些东西。这就是为什么会有很多怀旧情绪。

3.高中数学内容更加抽象

当一个学生逐步进入高中数学学习之后，数学的学习内容逐步抽象化。在数学必修的第一章就包含了理论性以及抽象性等相关的难点知识。其中包括映像、集合等基础函数，紧接着是学习一次函数、二次函数、幂以及相应的指数函数，同时函数的方程应用等。高中数学的基础概念也在增加，数学符号更加复杂，对于学生的推理以及公式应用能力有较大的要求。在以此函数上，初中阶段只需要掌握其含义就可，一个简单的实数函数和取值范围的图就可以了。高中的时候，你学的一元二次函数比较深刻，增加了一个给定区间内二次函数最大值的问题，融入分类讨论的数学思维方法;有些会添加一个变量，由此产生的问题甚至更加多样化：有参数可以找到最大值和最小值或值的范围;有的转化为建立常数的问题;还有关于这个问题的存在的问题。本内容是初中数学函数部分的延伸和延伸。

二、高一学生数学学习适应性对策

1.优化环境以创造良好的生活学习氛围

我们作为教师必须直观的了解高一学生之间的差异，努力创造条件，使不同层次的学生有机会表达自己的意见，给予高一学生更多积极的动机和激励评价，鼓励学生进行积极探索并为学生的主见进行支持，与高一学生建立和谐的学习社区，提高高一学生的学习效率。作为家长，必须要习惯孩子在高中学习阶段的特征。需要逐步从小学、初中进行实质的转变。在这样的过程中，校长以及学校就起到了实质的桥梁作用。因此学校组织的家长会或者家校联合活动，需要突出对学生的心理特征以及学科特征进行指导，这些措施将会有助于家长加强对学生的了解。

2.用趣味性不断改进数学教学方法

在数学的实际教学过程中，需要开展多元化教学以及分析教学，或者启发式的教学方法，这三者可以交替运用，让学生逐步在数学学习过程中养成良好的思维习惯以及数学情感，逐步做到灵活运用新的数学知识。同时可以结合多媒体技术，通过声音或者图像、动画的形式加以表达，活跃数学课堂教学，逐步为学生创建一个充满活力、朝气蓬勃的数学课堂，营造更具趣味性的数学学习环境，以此实现改变传统的数学教学模式，摆脱单调性。最终实现提升学生的数学学习能力以及数学思维，增强其数学学习的自信心。现在，数学教科书每章都有信息技术选项。

如下例：

有关部门可以用什么方法来检测特定林区松鼠的繁殖情况？在这些问题的基础上，同学们开始认真思考和设计方法。经过大约10分钟的思考，有同学想出了一个很好的主意：捉100只松鼠，做个标记，然后放回去。过了一会儿，你可以从林区抓到50只松鼠，找到50只松鼠。有标记的动物有4只，因此估计这片林区有1250只松鼠。

教师可以支持学生的思维，因为在实际的捕获活动中，每一只松鼠被捕获的几率基本上是一样的，这涉及的是基础的概率，实际计算如下。

设林区有n只松鼠，那么由

因此可以得出，学生不仅仅对这种乐趣以及有挑战性的题目感兴趣，还能逐步激起学生的探索兴趣以及相应的好奇心，让学生变得更活跃。

3.构建回归生活的实践性教学

在数学学习的过程中需要通过层次的积累，并对自身的不足加以检验。从零基础开始，通过简单的问题设置，逐步养成独立思考的良好习惯，做好总结。它要求教师;灵活使用生活中的现象，实例，实地研究，实验和其他方法，以使学生营造强烈的数学生活氛围，并将数学教学融入到自身的实际生活之中。

问题：常识告诉我们，人的身高越高，体重越重。那么平均来说，身高170 cm的人比身高160 cm的人体重大多少呢？全国青少年身高（cm）与体重（kg）的数据。（1）根据数据作出散点图，讨论散点图呈现的趋势;（2）选用一个函数来近似描述身高与体重的关系;

问题（1）和问题（2）已经给出了相对明确的解题方向，只要教师给予正确的引导，学生很容易在问题中找到突破口。这两个问题的答案就是模型构建的过程。

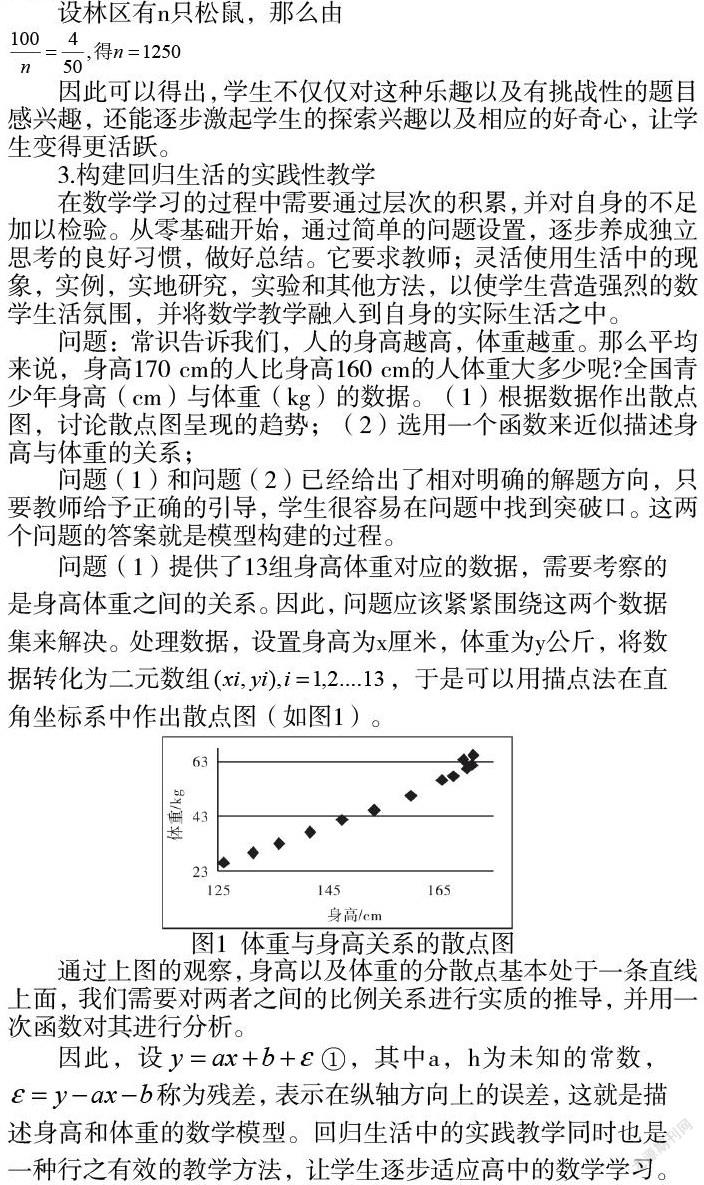
问题（1）提供了13组身高体重对应的数据，需要考察的是身高体重之间的关系。因此，问题应该紧紧围绕这两个数据集来解决。处理数据，设置身高为x厘米，体重为y公斤，将数据转化为二元数组 ，于是可以用描点法在直角坐标系中作出散点图（如图1）。

通过上图的观察，身高以及体重的分散点基本处于一条直线上面，我们需要对两者之间的比例关系进行实质的推导，并用一次函数对其进行分析。

因此，设 ①，其中a，h为未知的常数， 称为残差，表示在纵轴方向上的误差，这就是描述身高和体重的数学模型。回归生活中的实践教学同时也是一种行之有效的教学方法，让学生逐步适应高中的数学学习。

结语：综上所述，一般来说，对于一些高一学生来说，尽快熟悉和适应高中数学并不是一件容易的事。然而，作为一名教师，我们需要从积极乐观的角度看待高年级学生的学习调整过程。因为学生从不擅长数学学习到非常适应的过程，也是一个重塑自我的过程，让学生发展自我、突破自我、提高自我。

参考文献：

[1]仇勇.高一学生数学学习适应性困难的原因及对策[J].试题与研究，2019（32）：128.

[2]马东邦.浅析高一数学教学中对学生学习适应性的培养[J].数学学习与研究，2015（13）：49.