大学新生数学学习适应性的调查研究
季燕萍
摘 要:文章通过对大学新生数学学习情况的调查,利用统计软件SPSS17.0进行数据分析,了解学生数学学习适应状况,分析任课教师、学生学习适应性及考试成绩的相互关系,并对大学数学教师和管理者提出相关建议,做到“以教适应学生的学”。
关键词:大学新生;数学;学习适应性;教学建议
中图分类号:G642.0 文献标识码:A 文章编号:1002-4107(2015)08-0016-03
大学数学作为高等院校各专业的一门必修的重要基础课程,它培养学生的数学应用能力,特别是针对各专业的实际问题,建立数学模型,运用数学软件进行计算,综合运用所学知识分析解决实际问题的能力,是学生学习后续专业课程的基础[1]。但是由于数学知识的深刻性、抽象性、广泛性,近年来,据高校任课教师反映,大学新生对数学的学习普遍感到困难,学习兴趣弱,成绩下降明显。为了引导和帮助新生尽快适应数学的学习,作为大学数学的教学及管理者,我们除了在教学方法、教学内容、教材使用等方面进行改革之外,还要了解新生的学习特点,分析学生在学习适应性方面存在的问题,加强和改革数学教学管理,提高教学质量,为学习后续课程打下坚实的基础。
一、研究内容及方法
一般认为,学习适应性是指学生在学习过程中根据学习条件(学习态度、学习方法、学习环境等)的变化,主动做出身心调整,以求达到内外学习环境平衡的有利发展状况的能力[2]。本文从大学新生对数学学习的态度(包括学习动机与兴趣、学习计划、作业态度、听课态度等)、学习过程中的方法(主要从听课、笔记、作业、复习、总结归纳等方面反映)、对任课教师教学方法的适应性(主要从提问、总结等具体教学环节及整体上考察)三个维度进行调查,了解学生学习的适应状况,并利用统计软件SPSS17.0进行数据分析,研究学习适应性与考试成绩的相关性,分析教师对学习适应性及成绩的影响。通过探索彼此之间的关系,发现数学教学中存在的问题,提出相应的建议,从而不断地提高数学教学质量。
本文参考华师大心理系周步成教授等人修订的学习适应性量表(AAT量表),并借鉴扬州大学研究生袁洲的硕士毕业论文《高中、大学数学学习衔接问题的研究》,编制了大学新生数学学习适应性调查问卷。问卷共设置30个问题,总计150分,分别从学生的学习态度(13题,共65分)、学习方法(10题,共50分)、对教师教学方法的适应性(7题,共35分)三个方面设计。要求被调查者从 “完全符合、基本符合、说不清楚、基本不符合、完全不符合” 五个选项中选出最符合自己实际情况的一项。并赋予“5、4、3、2、1”的分值,得分愈高,表示适应性愈强。
笔者以扬州大学数学学院、信息工程学院、物理学院、化学学院、农学院、环工学院6个学院的13个专业、19个不同班级的2013级新生作为问卷调查的对象。共发放问卷592份,收回578份,其中有效问卷560份。为了更为真实、客观地反映新生对数学课程的掌握程度,文章从学校教务系统内导出所有被调查对象的2013—2014第一学期数学期末成绩作为成绩数据,进行分析。同时,我们查找到该学期的教学任务,找出对应的任课教师编号,本文以教师编号替代教师真实姓名。
二、研究的结论与分析
(一)大学新生数学学习适应性的状况
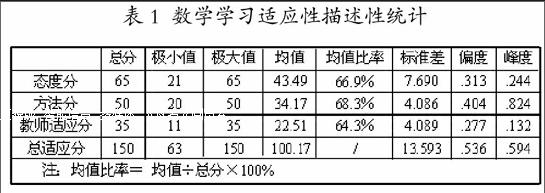
用频数(Frequencies)分析的方法对调查问卷进行分析,得到每题选项的百分比。汇总学习态度得分、学习方法得分、对教师教学方法的适应性得分、学习总适应得分(态度分、方法分和教法适应分之和),得到各汇总分的均值、标准差及偏度系数等相关数据,见表1。
表1 数学学习适应性描述性统计
从选项百分比及表1我们可以看出:
1.学生学习总体适应分的均值为100.17,适应性水平不高;标准差为13.593,极差为87,分化程度较大;偏度系数为0.313,大于零,正偏,表明总体得分偏低。
2.学习态度分均值为43.49,极差为44分,标准差7.69,为三项因素中最大值,说明学生在对数学学习态度上差别很大。通过分析,尽管有87.2%的学生认识到“大学数学的学习的确非常重要”,但是学生对数学的学习兴趣却处于中等水平, 63.9%的学生认为现在学习数学的勤奋程度同高中相比明显下降。
3.对于数学学习方法,尽管有58.8%的学生认为“原来高中的学习方法不适用于大学数学的学习”, 但仅有18.9%的学生找到了合适的学习方法。只有四成的学生在学习新概念时,会把学过的相关知识联系起来对照、比较和分析。
4.对教师教学方法的适应性分均值比率为64.3%,
为三项因素均值比率最低,学生对教师的教学方法适应性最低。只有11.3%的学生完全适应大学数学教师的授课方式。
(二)学生数学学习适应性与成绩的回归分析
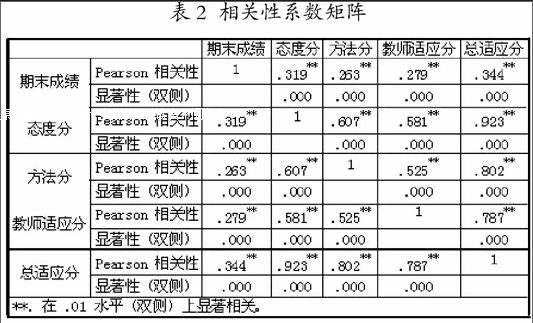
用回归分析法研究学生学习适应性的三项因素与数学成绩之间的相关关系,寻找出哪些因素对数学成绩的影响最为显著。通过SPSS统计软件中“分析—相关—双变量”得到表2。
表2 相关性系数矩阵
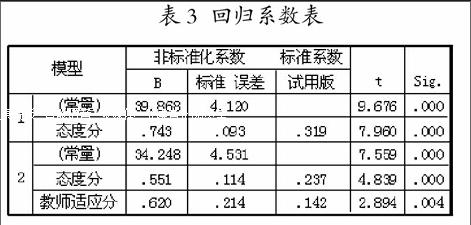
表3显示,“**”为p<0.01,相关极其显著。说明数学成绩与学习适应性的三项因素之间存在显著的相关关系。单击“分析—回归—线性”菜单项,进行因变量和自变量的回归分析,建立最优的回归方程。根据样本数据的计算结果,得到表3。
表3 回归系数表
系统先将与因变量Y(期末成绩)关系最密切的自变量X1(学习态度)引入模型,建立Y与X1之间的一元线性回归模型1:Y=39.868+0.743*X1,而后又引入X3(对教师教法的适应性),从而建立了Y与X1、X3之间的二元线性回归模型2,得到回归方程:
Y=34.248+0.551*X1+0.62*X3
回归结果表明,学习态度和对教师教法的适应性这两个因素对数学成绩的影响达到显著性水平。学习方法虽然与数学成绩之间存在显著的线性相关,但在建立的模型中却未被加入,说明它对成绩的影响未达到显著性水平。另外,回归系数的显著性水平皆小于为0.05,说明建立的回归方程是有效的,可用于对因变量值的预测。
(三)不同任课教师的学生学习适应性及成绩的差异性分析
上面我们分析到学生对教师的教学方法适应性最低,在这里我们重点分析一下不同的任课教师,学生数学学习的适应性及成绩有无差异性?对学生学习适应性及考试成绩分别会产生怎样的影响?为了回答此问题,首先我们对数据按“教师编号”进行拆分,利用SPSS中的描述性统计,得出表4。
表4 不同任课教师的学生学习适应性、成绩描述性统计
我们运用Kruskal-WallisH检验,对不同任课教师的数学学习总体适应、期末成绩差异性分析,渐近显著性(2-sided)p=0.000,拒绝原假设,认为差异非常显著。
可以看出,不同的任课教师,学生的数学学习适应性和成绩差异非常显著。学生学习总适应分的均值在94.16分到104.79分之间,适应性水平偏低,标准差在9.110到15.688之间,两极分化现象比较严重。期末成绩亦然。虽然学生的期末成绩来自不同的课程,试卷的难易程度也不一样,学生的成绩固然会有一定差距,但是我们还是不难发现,像33号教师,所授班级学生的平均成绩只有61.49,是所有均值的最低分,并且学生的总适应分均值94.16,也为最低。而27号教师班上的学生成绩均值为88.65,标准差为9.586,是所有任课教师所授的学生成绩最好的,差异性也为最小,学生的总体适应均分为104.79,为最高值,学生对该教师的教学最为适应。通过进一步分析,我们发现两位教师所授学生对教师教学方法的适应性,27号教师均值为24.3,而33号教师均值为20.0,是三项因素中均值差异性最大的一项,学生对33号教师的教学方法最为不适应。有68.7%学生认为27号教师的提问能激发他们的积极思考,而对33号教师,只有29.4%学生认同。半数学生认为33号教师的教学方法比较单调,只有13.9%的学生认为27号教师方法单调。
三、反思与建议
通过以上的分析,大学新生数学学习的总体适应性水平不高,在学习态度上表现为很大的差异性,对教师的教学方法适应性最低,而任课教师对学生的学习适应性和成绩影响非常大,学生的学习态度和对教师教法的适应性对数学成绩的影响非常显著。如何让我们的大学新生更快地适应数学学习、取得更好的学习成绩,这就要求我们教师和管理者要努力提高教学管理水平,做到“以教适应学生的学”。笔者认为可以从以下方面进行。
(一)帮助学生端正学习态度
大学新生刚经历了“两耳不闻窗外事,一心只读圣贤书”的高中时代,许多学生在心理状态上存在放松情绪,学习态度松懈,无学习目标和动力,缺乏对自己能力和知识水平的客观认识;同样,许多新生一开始对大学生活充满憧憬和向往,但是进入大学后发现,大学并不是自己想象的那样,大学高深的知识学习现实告诉他们,要学有所成,仍然需要付出艰辛的努力,学生心理上存有挫折感和失败感,尤其对难度较大的数学课程更是缺乏学习热情。在调查中,只有45.3%的学生“对大学数学感兴趣”,且过半数的学生认为自己现在的数学学习比较被动,在27号教师所授学生中,有89.5%的学生选择了“积极思考老师提出的问题”,而对33号教师,只有48.9%的调查对象做出同样选择。积极的态度不会自动涌现,它需要我们的教师或教学管理者在教学教育过程中去激发、去培养。教师可通过理想信念教育、专业思想教育等形式帮助学生端正学习态度,调整学习心态,增强学生的内部动力,使之尽快进入学习角色。并通过鼓励、鞭策、教导等手段充分调动学生的非智力因素,激发学生的学习热情[3]。
(二)着力改进教学方法
我国自上世纪90年代以来,进行了一系列教学改革,取得了众多成绩,但教学方法的改革虽有不少试点,却尚无明显的突破。灌输式、保姆式、应试型的教学方法目前仍占据着讲坛,严重影响着创新人才的培养[4]。数据分析显示,新生对教师教法的适应水平在三项因素中最低,存在着比较严重的不适应性,只有11.3%的学生完全适应大学数学教师的授课方式。33.2%的学生认为教师的教学方法比较单调,77.3%的学生认为“大学数学中的有些概念比较抽象,很难理解”。我们的任课教师不仅要加强专业知识的学习,更要加强对教育教学方法的研究,改变过去“填鸭式”教学方法,在课堂教学中引入研究性学习方法,即在好奇心驱使下的、以问题为导向的、学生有高度智力投入,且内容和形式都十分丰富的学习活动。研究性学习的教学方法能更好地实现从讲堂到学堂的空间转变、从先教到先学的时间转变、教师从“教授”到“教练”的角色转变[5]。真正把学生作为教学的主体,引导学生发现问题、提出问题、解决问题。
(三)注意教学内容的衔接
与高中数学相比,大学数学教学知识点较多,每堂课的容量较大,概念较为抽象,加之大量新数学符号的出现,逻辑语言的运用,使学生难于理解。在本次的问卷调查中,只有53.4%的学生选择“教师有时会让我们联系或对照高中数学的相关内容”。所以我们的教师在讲授大学数学内容时要注意与高中教学内容的联系,尽量避免知识梯度过大。并根据青少年认知发展阶段理论及已有研究,帮助学生剖析大学数学与中学数学之间的联系,在教学时向学生介绍相关内容的形成与发展,帮助学生进行意义建构。激活学生的先前经验,以降低学习难度,这样不仅可挖掘知识体系方面的联系,还可挖掘数学思想方法、数学观念方面的联系,提高学生的数学素养[6]。任课教师更应该关注高中课程内容的变革,对于某些高中未教但却是大学数学基础的内容,或者涉及的角度和侧重点不同,应及时补充,以免形成“空白”造成脱节。
(四)重视学习方法的指导
“授人以鱼,不如授人以渔”。教师不仅要将知识本身传授给学生,更重要的是指导学生如何运用学习资源,获得并使用有效的学习方法,进行创造性学习。作为基础的数学教学更应把传授学习方法、培养学生的自主学习能力作为重点。在调查中仅有18.9%的学生找到了合适的学习方法,前述33号教师所授的学生中,有76%的调查对象在大学数学课上,不管懂不懂,先把教师讲的内容记下。因此,我们的任课教师应全面熟悉和了解学生的数学学习实际,根据他们的认知特点及心理特点,把教学的重点放在启发思考、学习方法引导和辅导自学等方面,制定合理的教学目标,创设良好的学习环境,使大学生在教师指导下自觉、主动、创造性地学习。教师在指导时,应对学生学习的全过程和全方面进行指导,不仅要对学生的预习、听课、作业、复习、考试等系统学习的主要环节进行指导,帮助他们形成正确的学习方法和良好的学习习惯,还要明确提出对知识内容进行反思和回顾等学习要求,以将书中的知识内化为他们自己的知识结构。真正将大学生的学习引导为一种充分发挥其自身潜能的自主性学习,并成为其一生受益的学习能力。
参考文献:
[1]李映红.普通高校高等数学课程改革的思考[J].长春大
学学报,2011,(12).
[2]田澜.我国中小学生学习适应性研究述评[J].心理科
学,2004,(2).
[3]袁洲.高中、大学数学学习衔接问题的研究[D].扬州:扬
州大学,2005.
[4]马知恩.深化教学改革 加强师资队伍建设 培养高素质
创新型人才[J].中国大学教学,2011,(3).
[5]伍建华,汪世宏等.大学数学教学的现状调查和分析
[J].数学教育学报,2007,(3).
[6]原新生,牛保青.大学数学课程教学改革的实践与研究
[J].安阳师范学院学报,2010,(2).

