耦合双梁的非线性压电俘能器设计及仿真研究

张骁 沈辉 丁晓亮 曲鹏超

摘要：针对传统双稳态压电俘能器在低幅值激励下不易进行高能阱间运动的问题，设计了一种耦合双梁的非线性压电俘能器。利用集中参数法对系统进行了数学建模。对传统双稳态俘能器与本文所设计的俘能器进行了数值仿真，对比分析了两者在简谐激励与线性升频激励下的动态响应及俘能性能。仿真分析结果表明，通过调整系统结构参数，该非线性俘能器在工作频带内能够达到最大的平均功率。

关键词：非线性;压电俘能器;双稳态;磁力;弹簧

中图分类号：TN384

文献标志码：A

收稿日期：2020-09-07

基金项目：

山东省自然科学基金面上项目（批准号：ZR2017MEE039）资助。

通信作者：

沈辉，男，博士，副教授，主要研究方向为压电能量收集技术。E-mail： shenhui@qdu.edu.cn

通过压电俘能器收集环境中的振动能量来为无线传感器以及微机电系统供能具有很好的前景[1]。自然界中的振动往往不是固定在某个频率振动，而是在一个比较宽的振动频带下振动[2]。针对传统线性悬臂梁结构工作频带窄的问题，国内外学者做了大量的研究[3-7]。近些年来，有学者将目光转向非线性结构[8]，通过非线性磁力使压电悬臂梁系统呈现出双稳态。但是传统的双稳态系统需要较大的加速度激励，在低加速度幅值激励下只能在某个稳态振动（势能阱内运动），不能产生高能的阱间运动，俘能表现不佳[9]。本文在传统双稳态系统的基础上，设计了一种耦合双梁的非线性压电俘能器（Coupled Nonlinear Piezoelectric Energy Harvester，CNPEH），通过耦合弹簧有效降低了系统进行跨阱运动所需的最低加速度激励幅值。利用数值仿真法研究了结构参数对该俘能器在简谐激励以及线性升频激励下的俘能特性的影响。

1 系统的基本结构

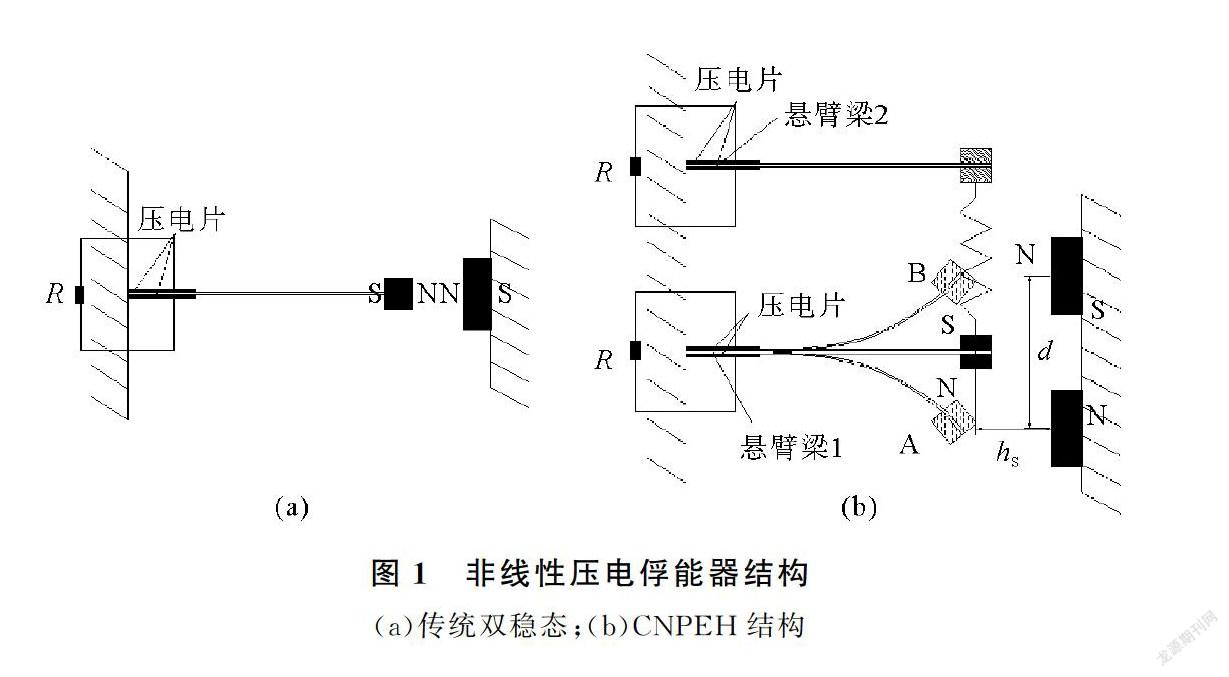
传统双稳态系统由单根悬臂梁、悬臂梁末端磁铁、外部磁铁以及压电片组成，末端磁铁质量块在外部磁力的作用下存在上下两个稳态位置[10]，如图1（a）所示。本文设计的CNPEH结构在传统双稳态系统的基础上，增加了一根悬臂梁，以及一根用来耦合两根悬臂梁的耦合弹簧，如图1（b）所示。该结构由悬臂梁1、2，压电片，永磁体，耦合弹簧和基座组成。末端带有永磁铁的悬臂梁1，在外部磁铁的吸引作用下，呈现两个稳态位置A、B。悬臂梁2末端为非磁性材料质量块，通过弹簧与悬臂梁1末端磁铁质量块连接。d为两个外部磁铁在水平方向的中心距，h为悬臂梁末端磁铁与外部磁铁在竖直方向的中心距，R为负载电阻。自由状态下，悬臂梁1自由端受到两块外部磁铁的吸力，整個系统处于不稳定的平衡位置。振动条件下，悬臂梁1在耦合弹簧、悬臂梁等效刚度和磁铁的吸力共同作用下达到稳态位置A、B[11]。

2 CNPEH的动力学模型

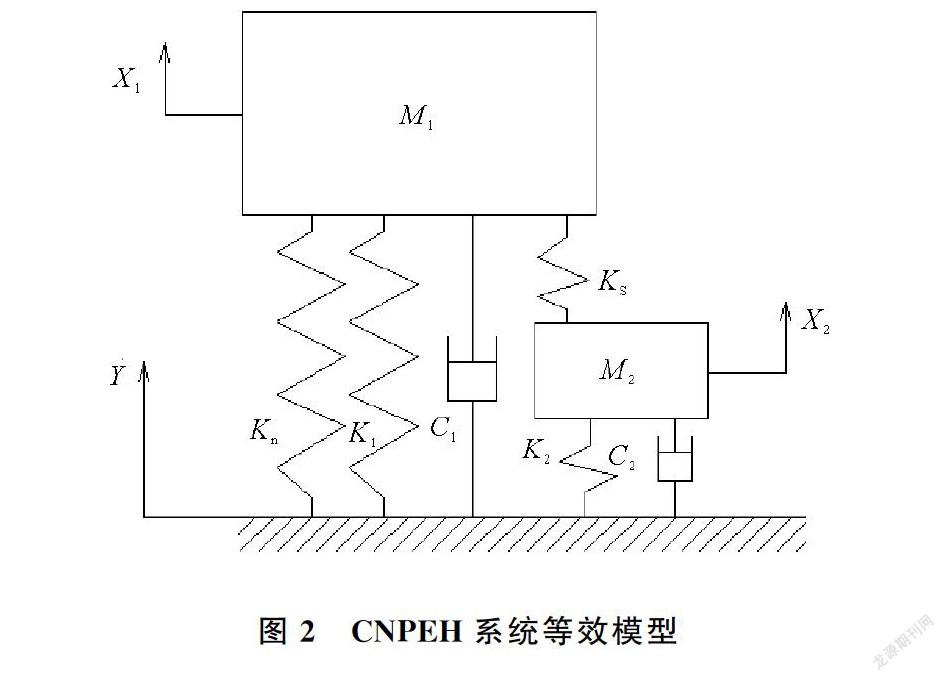
图2是CNPEH的动力学模型。CNPEH可以简化为两个弹簧—质量块—阻尼系统，两系统通过耦合弹簧连接。

运用拉格朗日方程和基尔霍夫定律，可得系统的机电耦合方程[12]

M11+C11+（Kn+K1）X1+KS（X1-X2）-KθV1=M1Cp1+V1R+Kθ1=0M22+C22+K2X2-KS（X1-X2）-KθV2=M2Cp2+V2R+Kθ2=0（1）

其中，M1 ，M2 ，K1 ，K2，C1 ，C2分别为悬臂梁1，2的等效质量，等效刚度，等效阻尼。Cp为压电片的电容，R为负载电阻。Kθ为机电耦合系数，Kn为磁斥力产生的非线性刚度，Ks为耦合弹簧的刚度。V1 、V2分别为悬臂梁1、2的输出电压，X1 、X2分别为悬臂梁1、2的末端相对于基础的位移，Y为基础激励。式（1）中的（Kn+K1）X1为弹性恢复力项Fr。式（1）中前两项若舍去耦合弹簧作用力，即耦合项Ks（X1-X2），此时，式（1）前两项为传统双稳态系统的机电控制方程

M33+C33+（Kn+K3）X3-KθV3=M3Cp3+V3R+Kθ3=0（2）

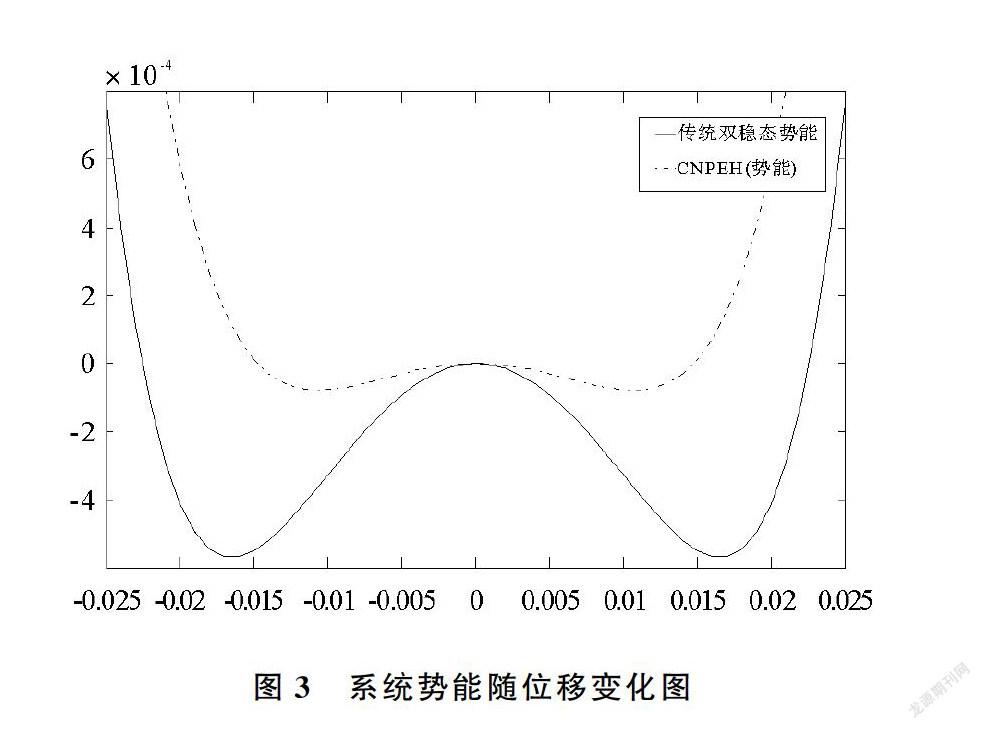
图3所示为两种双稳态系统的势能函数。同传统双稳态系统相比，CNPEH由于存在耦合弹簧作用力Ks（X1-X2），耦合弹簧会在势能函数曲线下降时积累势能，使得曲线上升的拐点提前，这样俘能器在较小的外界振动下就能跨越两个势阱振动，容易得到更宽的频带。

3 CNPEH的俘能特性

3.1 线性升频激励下俘能特性

线性升频激励表达式为

Y=A（2πf）2sin（2πft）（3）

其中，A代表加速度激励的幅值，频率范围为0～25 Hz。为了能正确对比CNPEH同传统双稳态系统的俘能特性，设置压电悬臂梁1、2的结构参数均与传统双稳态系统结构参数相同，即M1=M2=M3，C1=C2=C3，K1=K2=K3。选取加速度激励幅值A=0.3 g，耦合弹簧刚度Ks=0.2K1。

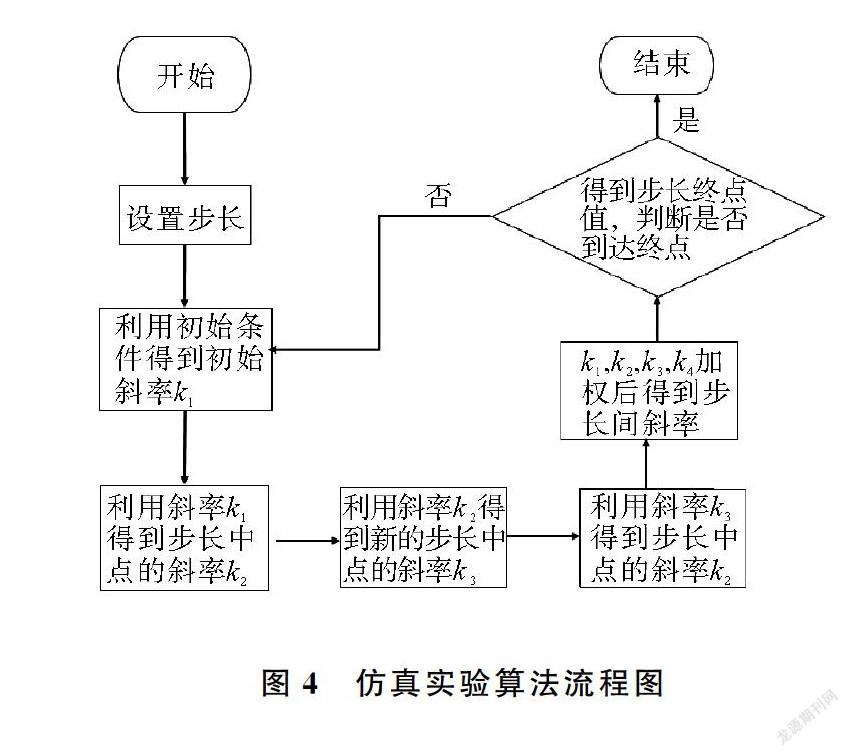
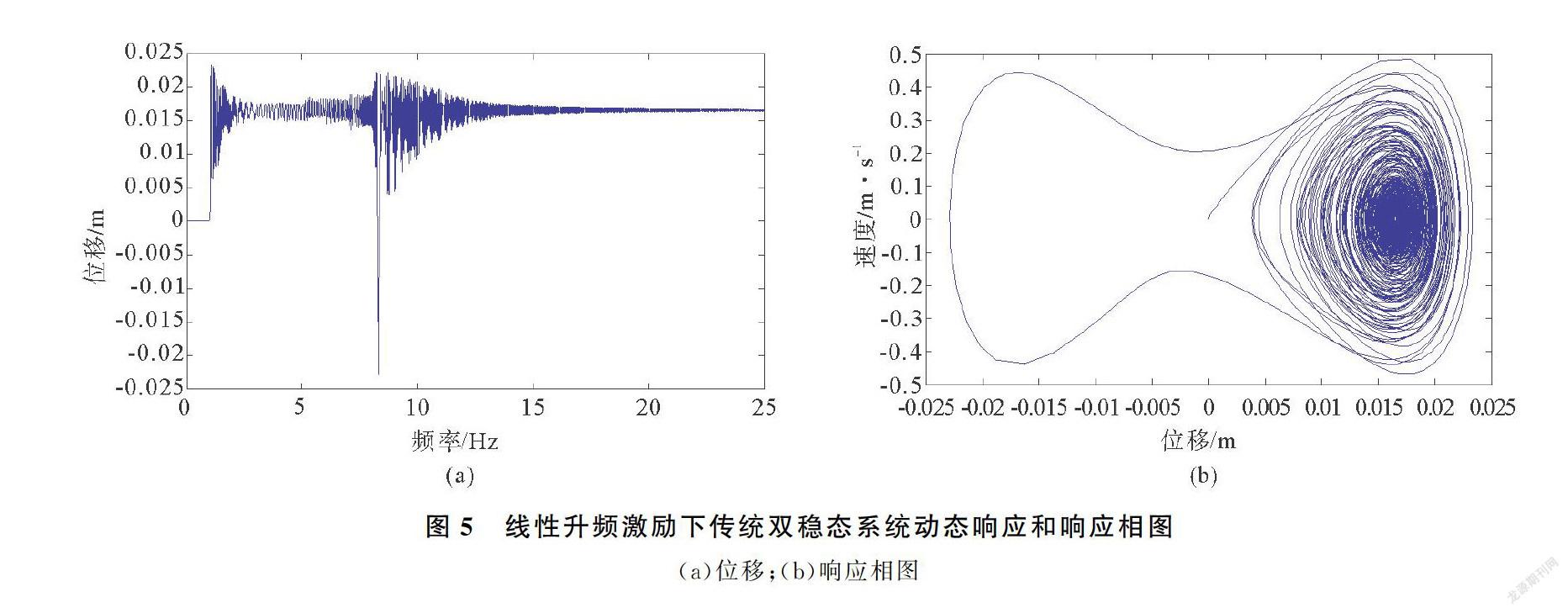
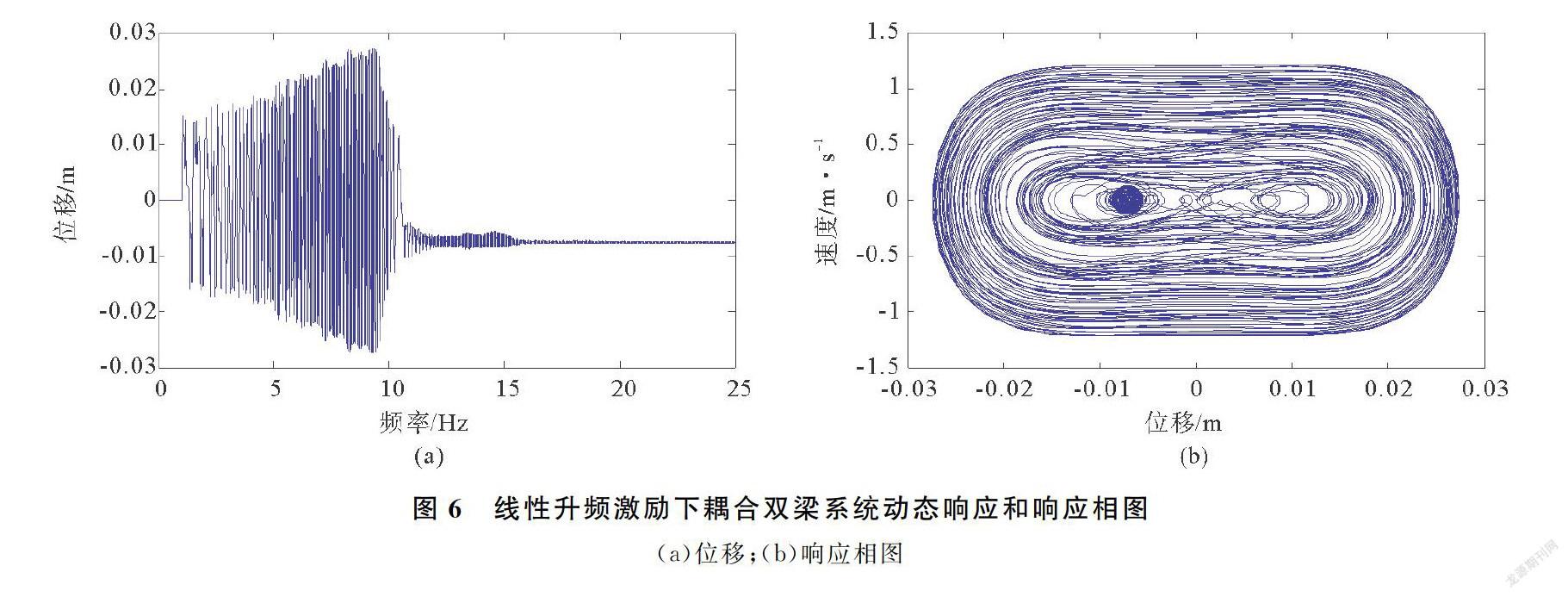
根据式（1）、（2）、（3），利用Matlab进行仿真计算。本文采用工程上广泛应用的高精度单步算法四阶龙格—库塔法进行仿真[13]，流程图如图4所示。CNPEH的结构参数如表1所示。分别计算得到传统双稳态系统和CNPEH系统的动态响应和输出电压。图5（a）和（b）分别为传统双稳态系统的位移时域图和系统响应相图。从图5（a）中可以看出传统双稳态系统没有达到足够大的能量越过势阱。系统在线性升频扫频下最终只能被限制在一个稳态位置运动。这点也可以从响应相图5（b）看出，只有在位移轴右半部有密集的响应相图的曲线。耦合双梁系统动态响应和响应相图见图6。

CNPEH系统中悬臂梁1末端受到磁力且出现双稳态现象，悬臂梁2仅受到耦合弹簧的作用并非双稳态系统，故着重比较悬臂梁1同传统双稳态系统的动态响应的差别。在相同系统参数下，CNPEH的悬臂梁1在激励幅值为0.3 g时可进行跨越势阱的大幅度运动。系统在3 Hz时已经进入工作频率，且一直持续到10 Hz，其工作频带可以达到7 Hz，电压最高可以达到10.7 V，如图6（a）所示。悬臂梁1也在稳态位置A、B之间做快速的大幅往复运动，如图6（b）所示。由于悬臂梁1的大幅往复运动，其由耦合弹簧所连接的悬臂梁2也呈现出一个类似双稳态的现象。悬臂梁2的俘能特性将在第4节介绍。通过对比两系统在同加速度激励下的动态响应表现，可知，CNPEH在低激励幅值下比传统双稳态系统有更好的俘能特性。经过仿真实验，得知传统双稳态系统需要在加速度激励幅值为0.58 g的情况下才有足够的能量来进行稳定的跨势阱运动。CNPEH能大幅降低系统进入跨阱运动所需的最低激励幅值。

3.2 简谐激励下俘能特性

设置简谐激励幅值A=0.3 g，频率f=8 Hz。在满足最低激励幅值的条件下，双稳态系统在简谐激励下想要进行稳定的大幅跨阱运动需要一定的初始条件。仿真实验得知，在基础位移0.02 m，速度为3 m/s的条件下，CNPEH中的悬臂梁1可以进行跨越势阱的大幅运动，如图7（a）所示。当系统趋向稳定时其产生的电压可以达到10 V左右，如图7（b）所示。

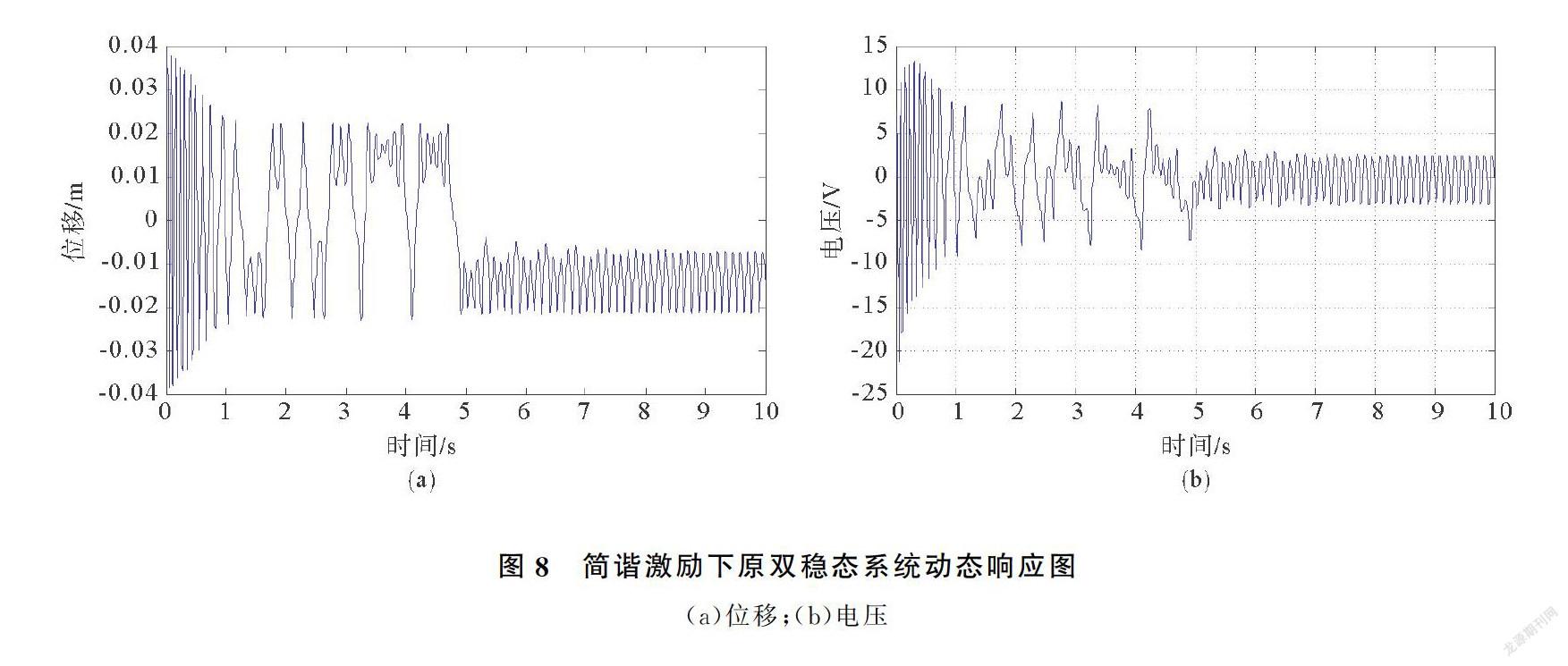
在同样的基础条件下，原双稳态系统无法进行跨越势阱的大幅运动，如图8所示。在初始条件下，仿真的开始阶段双稳态系统可以跨越势阱运动。但随着时间的推移、能量的耗散使得原双稳态系统的大幅跨阱运动变为双阱间的混沌运动，最终被限制在其中一个势阱中做小幅运动，如图8（a）。其稳定后最终产生的电压也仅仅只有2 V，如图8（b）。实际上，无论如何改变基础的位移、基础的速度，系统稳定后都不能进行跨越势阱的大幅运动，因其没有达到双稳态系统进行跨阱运动所需最低激励幅值。

4 耦合弹簧刚度对CNPEH的俘能特性影响

4.1 系统的平均功率表示

耦合弹簧刚度的改变会对整个CNPEH系统的俘能特性产生影响。为了表示不同弹簧刚度下的CNPEH系统的俘能特性差别，定义系统的平均输出功率为[14]

Pave = 1n∑ni = 1U2i R（4）

其中，Pave为输出功率，Ui为在取值点i的输出电压，n为取值点的个数，R为负载电阻。通过Pave来对比不同耦合弹簧刚度参数下系统的俘能特性。

4.2 不同耦合弹簧刚度的平均功率

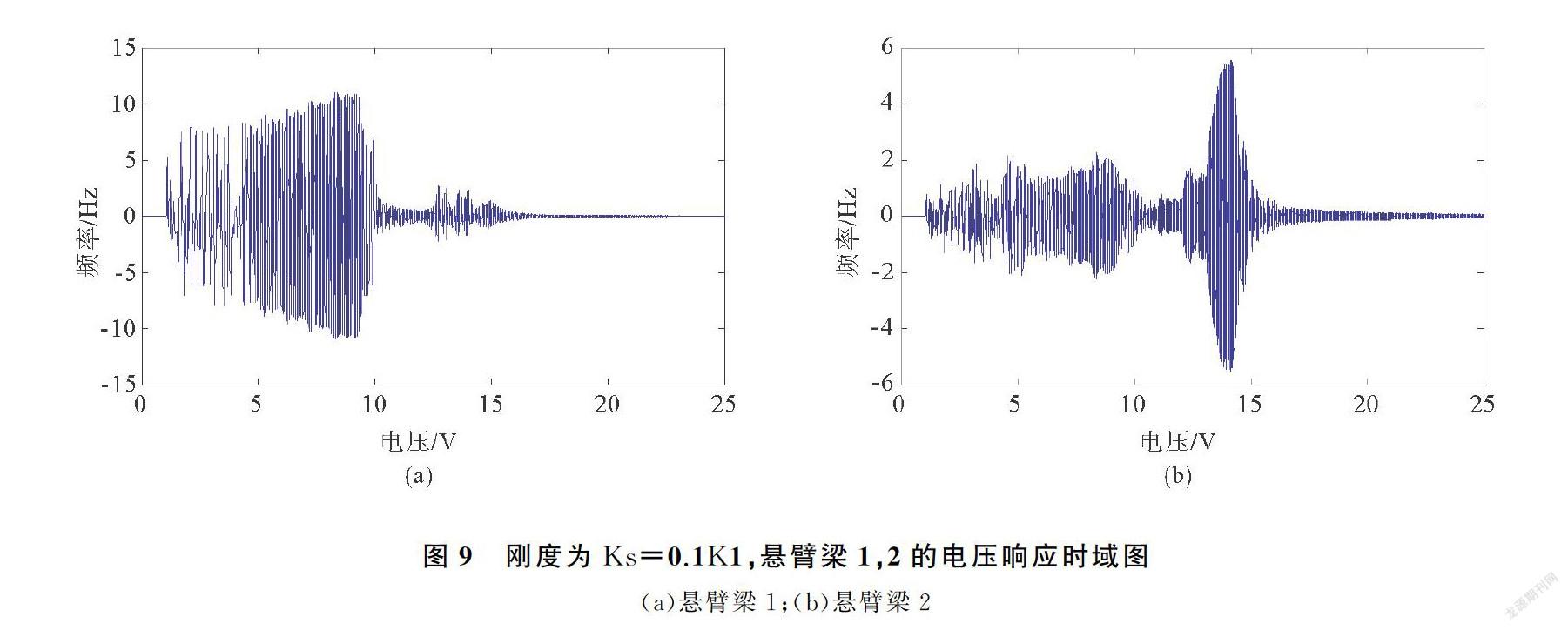
Ks=0.01K1时，耦合弹簧等效刚度可忽略不计，悬臂梁1实际等效为传统双稳态系统，悬臂梁2为传统线性压电悬臂梁系统，其工作频带在固有频率附近。此时两梁的平均输出功率为3 μW。当增大耦合弹簧的刚度至0.1K1，响应已经呈现出非线性的现象，如图9所示，并且悬臂梁2通过耦合弹簧受到悬臂梁1的影响，在非工作频带电压也有明显上升。此时的平均功率为21.5 μW。

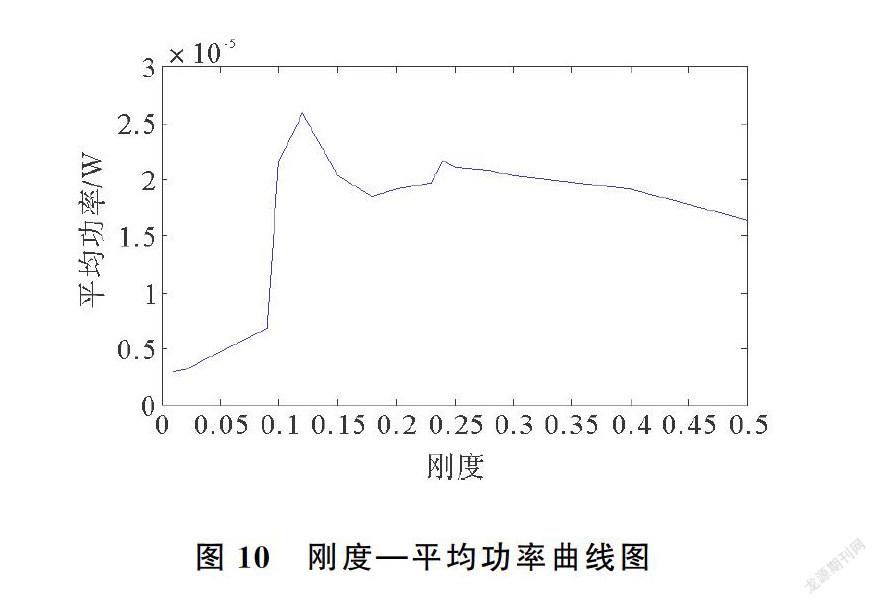
继续增大耦合弹簧刚度，俘能效率进一步提升，Ka=0.12K1时达到峰值，此时的平均功率为25.8 μW。继续增大Ks，悬臂梁2在耦合弹簧的影响下进一步呈现近似双稳态现象，但此时的悬臂梁1的俘能效率却因为耦合弹簧的增大而有所降低。这种趋势会持续到Ks=0.18K1。继续增大刚度Ks，此时悬臂梁1系统俘能效率对耦合弹簧刚度的敏感度降低，俘能效率的下降趋势减缓，但悬臂梁2对弹簧变化的敏感度增大，此时系统平均功率会随着刚度增大而增大，在Ks=0.24K1时达到一个新的峰值，平均功率为21.6 μW。之后，系统俘能效率会随着刚度增加而缓慢减小，图10是平均功率随耦合弹簧刚度变化的示意图。在实际应用过程中，不同的系统其最佳的耦合刚度可能不同，可以利用平均功率—刚度曲线找到最佳的耦合弹簧刚度使得系统处于最佳的俘能状态。

5 结论

本文构建了一种耦合双梁的非线性压电俘能器，建立了机电耦合方程，分析了传统双稳态系统与本文所设计的俘能器系统在相同激励参数下的不同表现，及不同耦合刚度下双梁耦合压电俘能器系统的俘能效率。双梁耦合系统的势阱阈值同传统双稳态系统相比降低50%。系统的俘能效率随耦合弹簧刚度变化，在线性升频激励下存在最佳耦合弹簧刚度使俘能效率最高。

参考文献

[1]ABRAMOVICH H， HAR-NES I. Analysis and experimental validation of a piezoelectric harvester with enhanced frequency bandwidth[J]. Materials， 2018，11（7）： 1243.

[2]TRAN N， GHAYESH M H， ARJOMANDI M. Ambient vibration energy harvesters： A review on nonlinear techniques for performance enhancement[J]. International Journal of Engineering Science， 2018，127： 162-185.

[3]ONG Z C， OOI Y X， KHOO S Y， et al. Two-stage multi-modal system for low frequency and wide bandwidth vibration energy harvesting[J]. Measurement， 2020，149： 106981.

[4]ZAYED A A A， ASSAL S F M， NAKANO K， et al. Design procedure and experimental verification of a broadband quad-Stable 2-DOF vibration energy harvester[J]. Sensors （Basel， Switzerland）， 2019，19（13）： 2893.

[5]王光慶， 崔素娟， 武海强， 等. 多稳态压电振动能量采集器的动力学模型及其特性分析[J]. 振动工程学报， 2019，32（02）： 252-263.

[6]吴义鹏， 季宏丽， 裘进浩， 等. 共振频率可调式非线性压电振动能量收集器[J]. 振动与冲击， 2017，36（5）： 12-16， 22.

[7]孙枫磊， 沈辉， 曲鹏超， 等. 新型双方向压电振动能量收集装置的设计与仿真[J]. 青岛大学学报（自然科学版）， 2020，33（1）： 12-17.

[8]徐振龙， 单小彪， 谢涛. 宽频压电振动俘能器的研究现状综述[J]. 振动与冲击， 2018，37（8）： 190-199， 205.

[9]ZHOU S， CAO J， INMAN D J， et al. Broadband tristable energy harvester： Modeling and experiment verification[J]. Applied energy， 2014，133： 33-39.

[10] YANG Z， YANG J. Connected vibrating piezoelectric bimorph beams as a wide-band piezoelectric power harvester[J]. Journal of Intelligent Material Systems and Structures， 2009，20（5）： 569-574.

[11] 張旭辉， 赖正鹏， 吴中华， 等. 新型双稳态压电振动俘能系统的理论建模与实验研究[J]. 振动工程学报， 2019，32（01）： 87-96.

[12] SEBALD G， KUWANO H， GUYOMAR D， et al. Simulation of a duffing oscillator for broadband piezoelectric energy harvesting[J]. Smart materials and structures， 2011，20（7）： 75022.

[13] 周生喜， 曹军义， ERTURK A， 等. 压电磁耦合振动能量俘获系统的非线性模型研究[J]. 西安交通大学学报， 2014，48（01）： 106-111.

[14] 蓝春波， 秦卫阳. 带碰撞双稳态压电俘能系统的俘能特性研究[J]. 物理学报， 2015，64（21）： 191-202.

Design and Simulation of Nonlinear Piezoelectric Energy Harvester with Coupled Double Beams

ZHANG Xiao，SHEN Hui，DING Xiao-liang，QU Peng-chao

（School of Mechanical and Electrical Engineering， Qingdao University，Qingdao 266071，China）

Abstract：

Traditional bistable piezoelectric energy traps are difficult to move between high energy traps under low amplitude excitation.To solve that， a nonlinear piezoelectric energy trap with coupled double beams is designed. Mathematical modeling of the system was carried out using the centralized parameter method. The numerical simulation method is used to analyze and compare the motion state and energy harvesting performance of the traditional bistable energy harvester and the energy harvester designed under simple harmonic excitation and linear up-frequency excitation. The performance of the energy harvester designed is studied under different system parameters. The Tesults indicate that the maximum power cutput can be obtained by adjusting srtucture parameter of nonlinear energy harvesting.

Keywords：

nonlinear; piezoelectric energy harvester; bistable; magnetic force; spring