基于IPSO-GPR的HVAC送风温度预测模型
寇腾跃 于忠清 杨熙鑫






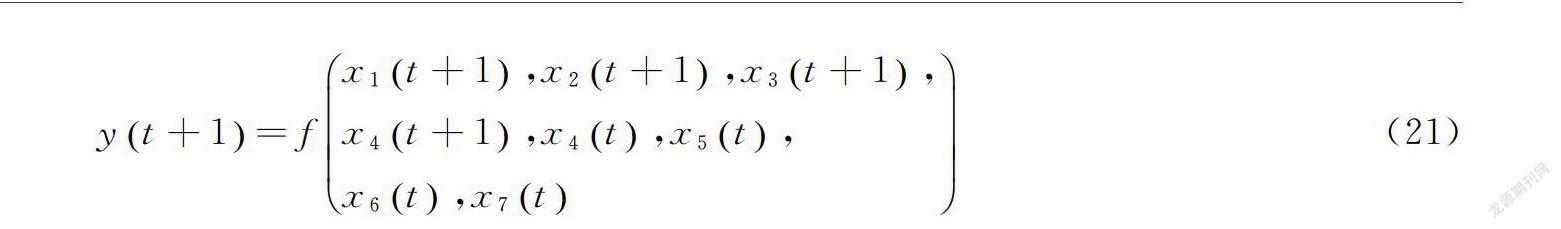

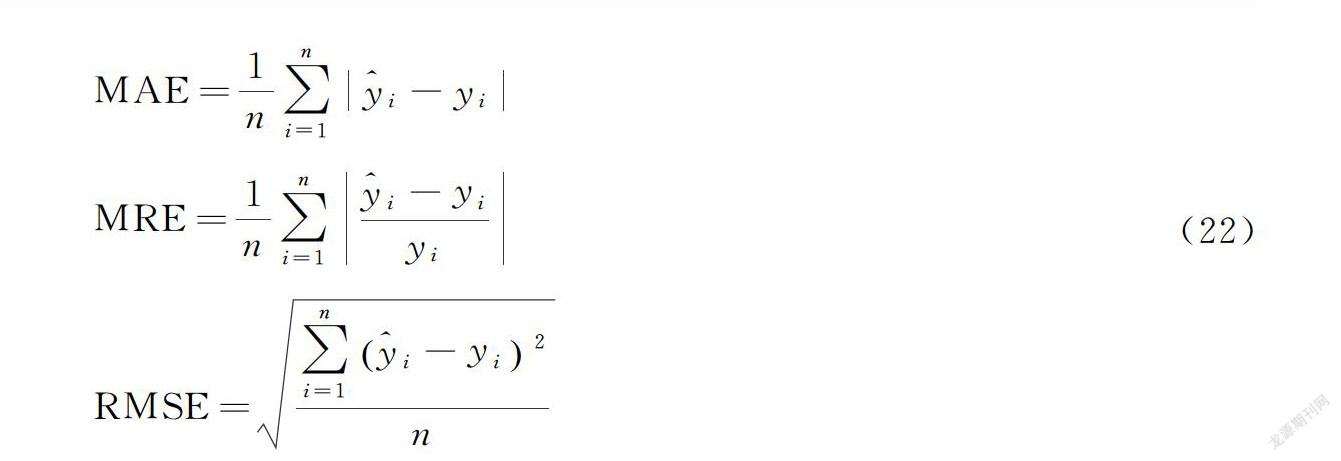




摘要:针对AHU系统中的多维、异构、非线性等特点,提出了一种基于改进粒子群的高斯过程回归(IPSO-GPR)算法。在传统的PSO算法上引进了混沌序列和交叉策略,使粒子在运动过程中能够自适应的调整搜索方向和速度,并针对局部最优解附近的区域进行了重点搜索,降低PSO陷入局部最优解的风险。使用平方指数和二次有理两种核函数的组合GPR来应对复杂的AHU非线性系统。对比PSO-GPR方法的预测性能,IPSO-GPR模型预测的送风温度误差保持在0.07℉以下,预测效果更加精确。
关键词:超参数优化;粒子群优化;混沌序列;高斯过程回归;暖通空调送风温度
中图分类号:TP399
文献标志码:A
收稿日期:2020-11-11
基金项目:
山东省重点研发计划(重大创新工程) ( 批准号:2019JZZY020101)资助。
通信作者:于忠清,男,博士,研究员,主要研究方向为嵌入式系统、普适计算、大数据。E-mail:1812661472qq.com
暖通空调(HVAC)中空气处理单元(AHU)影响系统整体性能和能耗[1]。在使用模型预测控制(MPC)降低AHU机组的能耗时[2],首先需要建立能耗和系统性能(送风温度,送风管道静压)的预测模型,然后在满足HVAC系统需求的前提下优化系统的控制以达到节能效果。系统性能预测模型的结果是优化控制的约束条件,如果系统性能的预测模型精度不够,就会产生相对错误的预测结果,优化控制模型为了满足错误的约束,就会产生偏离系统需求的控制指令,此时不仅能耗会有所增加,室内舒适度也会降低。为了使优化控制能够更加精确,需要建立高精度的系统性能预测模型。目前针对复杂的、非线性问题的预测方法包括:支持向量机(SVM)[3]、人工神经网络(ANN)[4]、神经网络MLP回归[5]等。但由于HAU系统不可控因素众多,如室外温度,设备性能,管道布置等问题专业的预测模型对现阶段的送风温度变化预测精度受限。在众多非线性回归算法中,GPR[6]是一种新兴的回归方法,相比ANN和SVM GPR更容易实现,超参数可自适应获取,GPR模型可以把送风温度看作众多因素导致的随机过程,使预测结果具有概率解释意义。然而,GPR算法存在优化效果对初值依赖性太强、迭代步长难以确定、易陷入局部最优等缺点。为了克服共轭梯度算法的不足,本文采用了改进的粒子群优化算法(IPSO)自动搜索模型的最佳超参数,使用平方指数、二次有理和两者组合核函数分别建立送风温度预测模型。
1 高斯过程回归预测模型
1.1 高斯过程
高斯过程是定义在连续域(时间/空间)上的无限多个高斯随机变量所组成的随机过程。对该性质简单的表示为,对于任意的n∈N+,任意一组随机变量xi∈X,i=1,2,3,…,n与其相应的Yx1,Yx2,Yx3,…,Yxn服从高斯分布。一个高斯过程由其均值函数μx=EYx和协方差函数Cx,x′=EYx-μxYx′-μx′来表示。高斯过程
f(x)~GP(μ(x),C(x,x′))(1)
其中,x,x′∈X属于任意的随机变量。
1.2 高斯过程回归
有n个观测值的训练集D,假设输出值与其实际值之差为ε,则高斯过程问题的一般模型为
yi=f(xi)+εi,i=1,…,nRd→R(2)
其中,xi∈X是d维输入向量,yi是输出标量,ε是符合高斯分布的独立随机变量,ε~N(0,σ2n)。
基于贝叶斯线性回归框架 f(x)=Φ(x)Tω,使用随机分布ω~N(0,Λ),通过式(1)可以得出观测目标值y的先验分布
y~N(0,Q=C+σ2nI)(3)
由式(3)得出的训练样本输出y与测试样本输出y*之间的联合高斯先验分布为
yy*~N0,C(X,X)+σ2nIC(X,x*)C(X,x*)C(x*,x*)(4)
其中,C(X,X)是n×n维对称正定协方差矩阵,其中,cij用于表示xi与xj之间的相关性,C(X,x*)是测试样本x*和所有训练数据X的n×1维的协方差矩阵,C(x*,x*)是测试样本x自身的协方差矩阵。
在给定测试样本x*和训练集D的条件下,贝叶斯概率预测的目标是计算&(y*|D,x*),根据贝叶斯后验概率
&(y*|x*,D)~N(μy*,σ2y*)(5)
其中,y*的均值和方差為
μt*=Cx*,XC(X,X)+σ2nI-1y,(6)
σ2y*=Cx*,x*-CTx*,XC+σ2nI-1Cx*,X(7)
高斯过程中要求协方差函数在有限输入点中是正定的,满足Mercer条件的对称函数。根据Mercer定理,协方差函数等于核函数。高斯过程中有两类核函数:ARD(自动相关性确定)核函数和ISO(各向同性)核函数[7]。在ARD核函数中超参数的每个分量ξi对应于X的xi,而ISO核函数的超参数ξ始终是一维标量,所有输入和输出的相关性都是相同的。为了减少超参数的数量,提高模型的计算速度,在AHU送风温度预测的问题中,各参数与送分风温度之间呈现高度非线性关系,单个核函数很难准确找到数据内部的所有特征关系,本文采用了不同的ISO核函数对该问题进行优化解决。
平方指数核函数(squared exponential,SE)
CSExi,xj=σ2fexp-xi-xj22+σ2nδij(8)
二次有理核函数(rational quadratic,RQ)
CRQxi,xj=σ2f1+xi-xj22α2α+σ2nδij(9)
SE+RQ的组合核函数(Combined,CC)
CCCxi,xj=CSExi,xj+CRQxi,xj(10)
其中,σ2f为核函数的信号方差,用于控制局部关联度;σ2n为噪声方差;为核函数的相关性判定超参数;值越大,输入和输出的相关性越差;α为核函数的形状参数。δij是克罗内克函数。
1.3 最优超参数
将式(8)、(9)、(10)中出现的超参数组成θ{σ2f,,σ2n,α},传统的寻优方式是使用对数似然函数,可以对超参数θ进行优化。使用共轭梯度算法,通过最大化训练样本的对数似然函数来搜索最优超参数
Lθ=logpy|X,θ=-12yTQ-1y+12logQ+n2log(2π) (11)
对θ求偏导
θiLθ=12tr(ααT-Q-1)Qθi(12)
将求解的最优超参数θ带入式(6)和式(7),得到测试样本x*的预测值和方差。
2 模型超参数寻优问题的求解
目前,由式(11)和式(12)获得GPR的超参数的方法对初始值的依赖性过强,难以确定迭代步骤以及易于陷入局部最优的缺点。本文用改进的粒子群算法(IPSO)在样本训练过程中自动搜索GPR模型的最优超参数,建立IPSO-GPR模型,以克服共轭梯度算法的缺点。
2.1 传统的PSO算法
PSO是基于群体和个体行为的优化算法,群体成员之间的信息共享能够提高群体的活动效率[8]。PSO算法使用了一组粒子进行并行搜索,每个粒子对应一个优化问题的候选解,都具有位置和速度属性。粒子根据其先前的移动经验以及同伴粒子的移动经验,按照当前的移动速度向着最佳方向移动。在N维搜索空间中,粒子i的位置和速度用向量Xi=xi1,xi2,…,xiN和Vi=vi1,vi2,…,viN表示,其中维数表示GPR预测模型中所需超参数的个数。Pbesti=xPi1,xPi2,…,xPiN和Gbest=xG1,xG2,…,xGN分别表示个体最优位置及全局最优位置。通常,在第n1≤n≤N维的位置变化范围限定在Xmin,n,Xmax,n内,速度变化范围限定在-Vmax,d,Vmax,d内。每个粒子的速度和位置更新计算公式
Vkin = ωVk-1in + c1r1Pbestin -xk-1in + c2 r2 Gbestn -xk-1in(13)
Xkin=Xk-1in+Vk-1in(14)
其中,Vkin是第k次迭代粒子i的速度矢量中的第n维分量;ω是惯性权重因子,用于调节对粒子当前状态的信任程度,ω越大,算法的全局搜索能力就越强,ω越小,局部搜索能力越好;c1和c2是学习因子,分别用于调节个体认知和社会认知的权重;r1和r2是两个取值范围为0,1的随机数,用于增加搜索随机性;Xkin表示第k次迭代粒子i的位置矢量的第n维分量。
2.2 改进的粒子群算法(IPSO)
由式(13)和式(14),参数的选择决定了PSO算法的主要性能。在传统的PSO算法中,参数ω、c1和c2设置为常数,因此PSO算法在对暖通空调的送风温度预测问题进行寻优和迭代过程中很容易丧失种群多样性,进而陷入局部最优解和过早收敛等问题[9],这会导致预测出的结果误差较大。本文提出了一种改进的粒子群优化算法(improved particle swarm optimization,IPSO),使用自适应策略和混沌序列对惯性权重和学习因子进行调整,引入遗传算法(GA)中的交叉思想,增加种群的多样性。
在粒子速度更新过程中,为了增强收敛特性,惯性权重因子ω通常被设计为线性减小,从惯性权重上界ωmax降到下界ωmin,自适应公式[10]
ωk=ωmax-ωmax-ωminkitermax(15)
其中,k为当前迭代数;itermax为算法最大迭代数,ωk为算法第k次迭代的惯性权重。
当学习因子c1>c2时,算法属于局部模型,此时收敛速度缓慢,但不容易陷入局部最优解。当学习因子c1<c2时,算法属于全局模型,此时收敛速度快,但更容易陷入局部最优解。为了保证算法的收敛速度和探索精度,将对算法采用先局部后全局的策略,算法前期提升搜索精度,后期加快收敛速度,自适应公式
ck1=c1,max-c1,max-c1,minkitermaxck2=c2,min+c2,max-c2,minkitermax (16)
其中,k为当前迭代数;itermax为算法最大迭代数,ck1和ck2分别代表算法第k次迭代的个体认知和社会认知的学习因子。
2.2.1 混沌序列在IPSO中的应用 混沌是一种确定性动力学系统因对初值敏感而表现出的不可预测的、类似随机性的运动。Ge等[11]应用混沌序列与量子秘钥相结合对图像进行了加密。Chen[12]使用混沌序列在加性高斯白噪声和码间干扰信道上进行了高效的通信。Alaa等[13]使用混沌序列提出了一种低成本、简单的真随机数发生器,并在密码系统中使用。混沌序列在各个领域中取得了良好的效果。
logistic混沌映射是能够体现混沌行为的动力系统之一
τk=μτk-11-τk-1(17)
其中,τk为第k次迭代的混沌参数,通常τk∈0,1; μ为控制参数,一般取值0,4。当μ的取值在3.56~4時,系统在0,1之间处于混沌状态,否则,若干次迭代后将会收敛到某个特定的数值,本文将μ的值设为3.6,4,τ0设为0.56。
由于混沌序列具有随机性、遍历性的特性。因此将混沌序列与式(15)、(16)相结合,利用混沌序列的遍历性提高全局搜索能力,减少算法陷入局部最优解的概率。结合混沌序列的自适应公式
k=τk·ωk(18)
k1=τk·ck1k2=τk·ck2 (19)
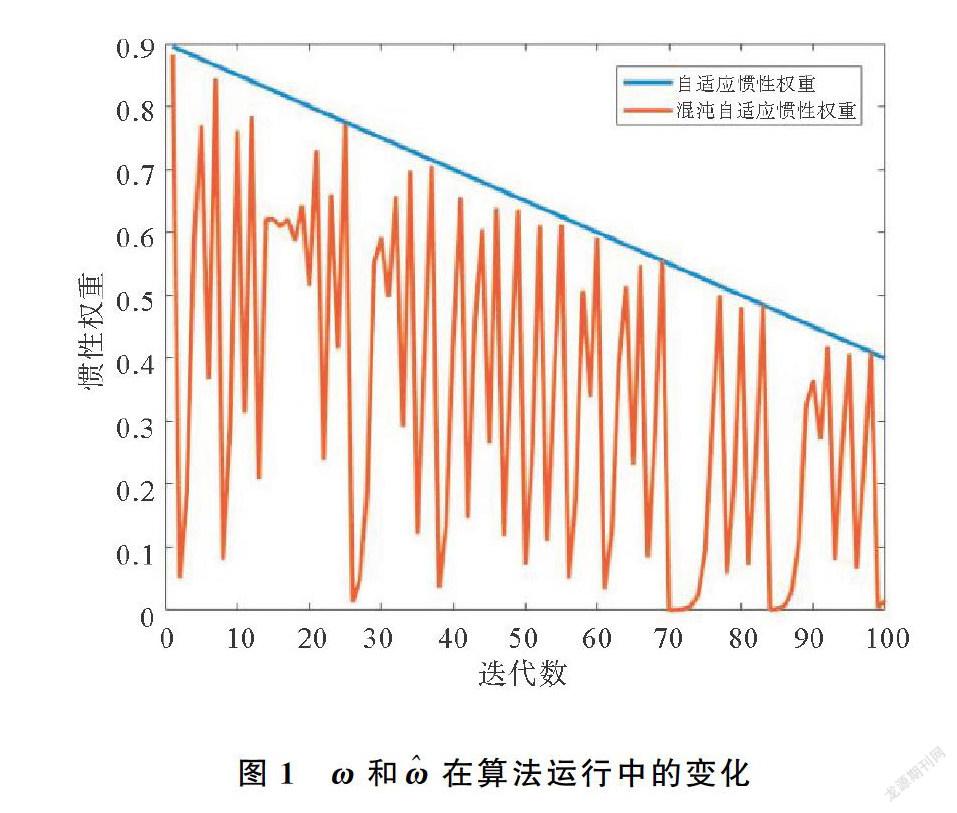
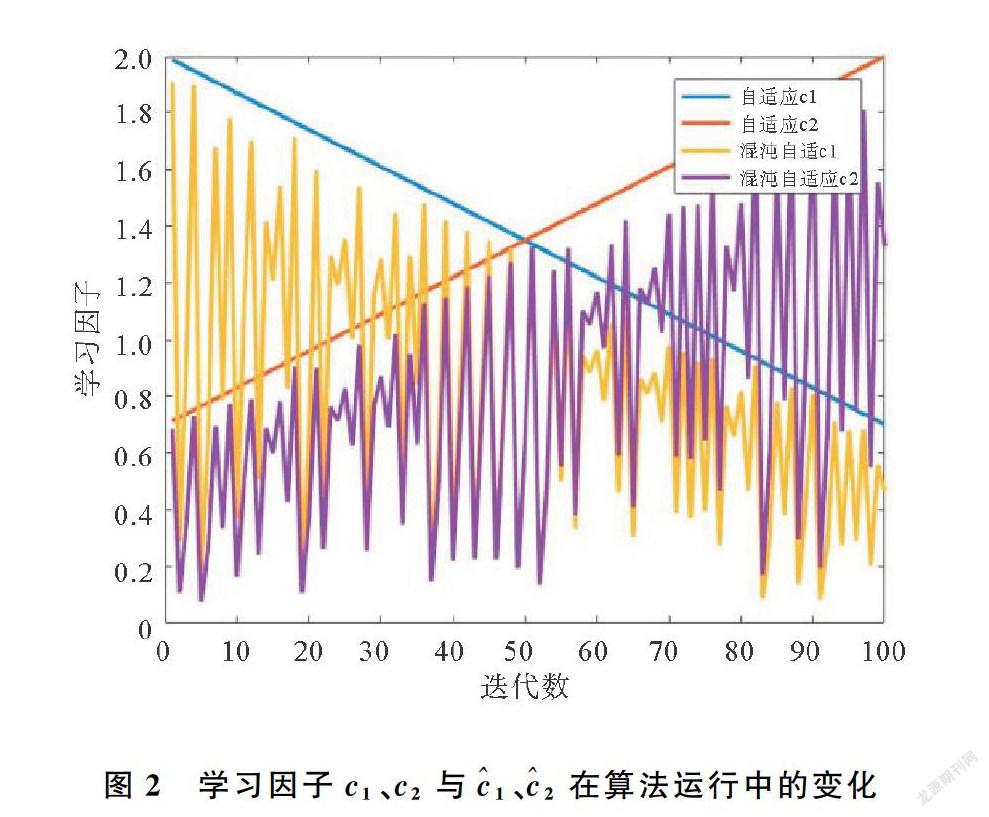
其中,k为IPSO算法第k次迭代的惯性权重;k1和k2分别代表算法第k次迭代的个体认知和社会认知的学习因子。在式(19)中,混沌参数τk将替代式(13)中的r1和r2。在式(15)、(16)中ω、c1和c2在自适应调整时,ω由ωmax向ωmin单调减小,c1和c2分别在自身范围内单调减小和单调增加,而在式(18)和(19)中,ω、c1和c2在单调减小或单调增加的同时进行震荡。传统的PSO的惯性权重因子ω通常设置为[0.4,1],学习因子c1和c2通常设置为2。本文将ω的搜索域定义在[0.4,1],学习因子c1和c2的搜索域定义为[0.5,2.5],使用传统的PSO对ω、c1和c2的最大值和最小值进行寻优,针对GPR模型中极值点较多的问题选用了rastrigin函数作为目标函数。结果确定了ωmax=0.9,ωmin=0.4,c1,max=2,c2,max=2,c1,min=0.7,c2,min=0.7。控制参数μ的取值在靠近4时,迭代产生的数值处于伪随机分布的状态,本文对4附近的多个值进行实验,结果表明在搜索ω和c1、c2过程中,控制参数μ的值分别在4和3.9时粒子群收敛效果最好,主要表现在收敛速度快且寻优精度高。如图1(itermax=100,ωmax=0.9,ωmin=0.4,μ=4,τ0=0.56)和图2(itermax=100,c1,max=2,c2,max=2,c1,min=0.7,c2,min=0.7,μ=3.9,τ0=0.56)所示,参数以混沌的方式覆盖整个递增线和递减线的下方区域,提高了算法的搜索能力。图3展示粒子的运动状态,粒子的速度和方向受参数调整影响,产生运动变化。
2.2.2 粒子交叉策略 为了增加种群多样性,本文借鉴了遗传算法中的交叉操作[14],从而有效的在解空间内探索和开发有前途的区域。算法每次迭代都向每个粒子分配一个0,1的随机数,当粒子Xkin的随机数不小于0.6时,Xkin进入交叉操作,对粒子位置矢量中的每个分量分配0,1的随机数,当位置分量xin随机数不小于0.5时,此位置分量xin被粒子个体最优的位置分量xpin所代替。图4给出了具体示例。
2.3 IPSO-GPR模型
IPSO-GPR模型算法流程图如图5所示。
Step 1 将数据样本分为两部分,85%数据作为学习样本,15%数据作为测试样本;
Step 2 初始化IPSO算法的参数,包括总迭代次数(itermax)、种群大小(N)、粒子速度和位置的变化范围、粒子的初始速度和位置。其中每个粒子代表一个GPR模型;
Step 3 根据每个粒子当前的位置信息,提取出GPR模型的超参数,通过GPR训练和测试样本; 然后预测测试样本的值;
Step 4 计算每个粒子(GPR模型)的适应度值fj,适应度函数采用平均绝对误差(MAE)
fj=1k∑ki=1i-yi(20)
其中,k为测试样本的数量,i是GPR模型对样本i的预测值,yi是样本i的样本标签值;
Step 5 将Step 4中计算的fi与迭代历史中计算的最优解fPbesti进行比较;如果fi<fPbesti,则用新的适应度值代替fPbesti,用新粒子代替以前的粒子;
Step 6 將每个个体最优解fPbesti与全局最优解fGbest进行比较;如果fPbesti<fGbest, 则用新的个体最优解代替原始的全局最优解,同时保存粒子的当前状态;
Step 7 判断算法是否满足预先设定的迭代步骤,如果满足,则结束算法,返回当前适应度值最小的粒子,同时解码获取超参数。否则进入Step 8;
Step 8 选取粒子进入交叉操作,交叉过程结束后,使用式(13)、(14)结合式(18)、(19)更新粒子的位置和速度。进入下一次迭代,迭代数加一;
Step 9 重复Step 3~Step 7,直到满足最大迭代步骤。结束算法,返回GPR模型的最优超参数。
3 实验验证
3.1 数据描述
本文所研究的暖通空调系统在某大学附属医院运行,该空气处理机机组总制冷量为122 500 BTU/H,总送风量为3 200 CMF,最大送风静压为979 Pa,送风机转速为1 834 rpm。传感器每隔1 min采集一次室
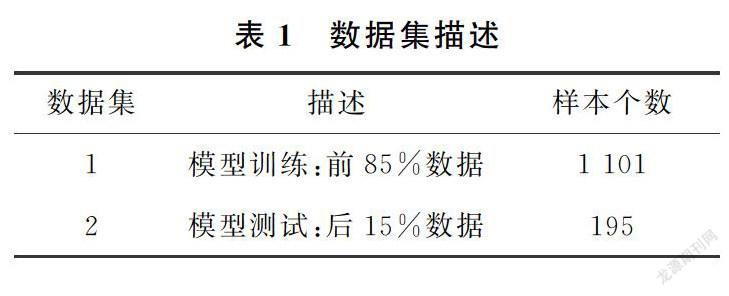
内温度、空气处理机组、加热和冷却设备等参数,将这些1 min频率下的数据转换为15 min的数据进行模型的训练和测试,转换后的数据集样本数量为1 296个。将数据集分为训练集(85%)和测试集(15%)。训练集用于选择所需特征参数和训练GPR预测模型。测试集用于计算IPSO算法中粒子的适应度以及评估模型准确性。所用数据集如表1所示。
3.2 参数选择
由于原始数据集包含了200多个参数,其中大部分的参数都与送分温度预测模型无关,不重要的参数会影响模型的准确性产生偏差。本文使用提升树(Boosting Tree)算法[15]进行参数选择,数据在每个节点被划分为两个样本,确立最佳分割,计算回归误差。并对后继树进行拟合,减少误差。在建立后继树的过程中,对每棵树的每个节点处的各个参数的重要性进行统计和归一化,参数重要性越高对模型的预测贡献越大。选择参数时,考虑了空调系统的设备状态和实际效果有一定的滞后性[16],由于数据的时间间隔为15 min,因此采用前一状态(15 min前)的参数值用来消除系统的延迟。表2总结了送风温度预测模型的最终输入参数。
3.3 实验描述和结果分析
实验中,送风温度的设定值保持在55.04℉(12.8℃)。送风温度预测模型
yt+1=fx1t+1,x2t+1,x3t+1,x4t+1,x4t,x5t,x6t,x7t(21)
其中,yt+1是指在t+1时刻的送风温度预测值。
根据图5所示的流程图,使用C++语言AILAB算法库编写IPSO-GPR算法程序。该算法库在对空调系统进行控制的过程中能够快速计算出需要发送的控制指令。IPSO的种群大小设置为50,惯性权重ωmax=0.9和ωmin=0.4,学习因子c1、c2的取值范围设为0.7,2。最大迭代itermax=300。GPR模型中超参数σf、、α、σn搜索空间分别为[0,100],[0,10],[0,10]和[0,0.05]。
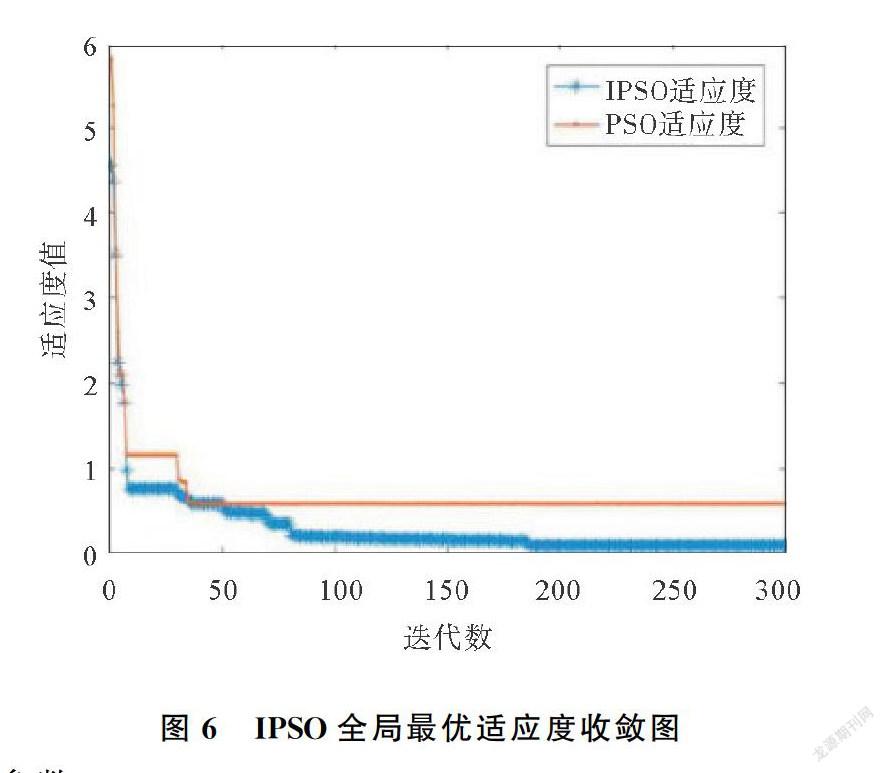
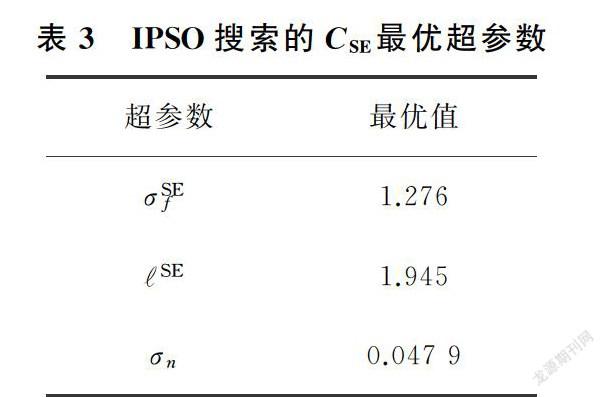
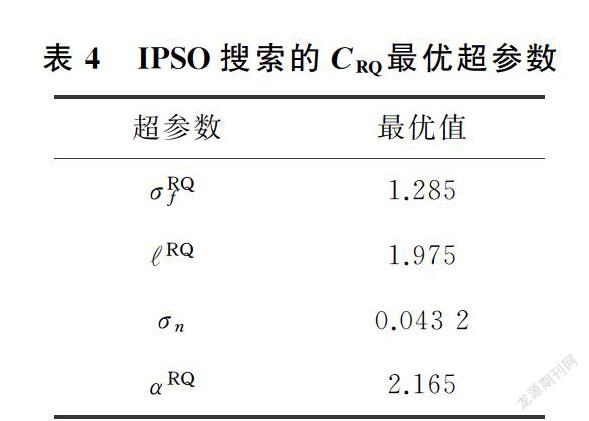
由于粒子群优化算法本身具有随机性,本实验运行10次IPSO-GPR,适应度值收敛到0.05。本文使用适应度与平均值相等的模型来进行预测分析。IPSO算法和PSO算法的比较结果如图6所示,可见适应值的减小过程是对GPR超参数的优化过程。适应值越小,回归精度越高。IPSO算法适应度值在前100次迭代中快速下降。在第200次迭代之后几乎不再有变化,适应度值几乎收敛到0.05,每次迭代全局最优的适应度值在0.002以内轻微震荡,此时已经找到了更高精度的最优超参数,表3、表4、表5中所示分别展示了CSE、CRQ和CCC的最优超参数。
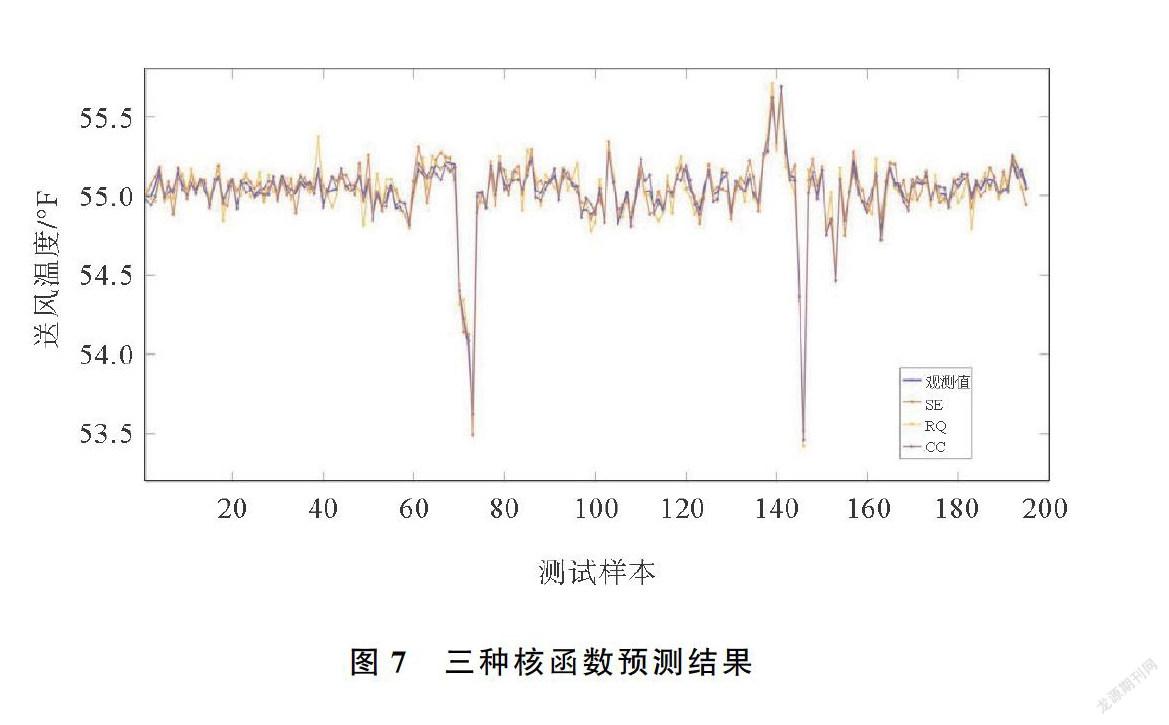
使用表3、表4、表5中的超参数对三种不同核函数的IPSO-GPR模型性能进行验证,图7展示三种不同核函数的IPSO-GPR模型对送风温度预测的结果,可以看出三种不同的核函数的预测模型结果都很理想。
为了进一步分析和评价IPSO-GPR算法的预测性能,采用三个指标来评估预测结果:平均绝对误差(MAE)、平均相对误差(MRE)和均方根误差(RMSE),MAE表示了预测值与实际值的相似程度,而RMSE则表示了预测值与观测值之间的总体偏差。MRE是预测送风温度的准确性的无单位度量[17]。值越小,预测效果越好
MAE=1n∑ni=1i-yi
MRE=1n∑ni=1i-yiyiRMSE=∑ni=1i-yi2n(22)
其中,n为测试样本的数量,i是IPSO-GPR模型对样本i的预测值,yi是样本i的样本观测值。
表6为不同核函数的IPSO-GPR和PSO-GPR以及GPR预测模型的评估结果,表明使用组合核函数CCC的IPSO-GPR对送风温度的测试样本进行预测,模型精度优于CSE和CRQ的IPSO-GPR。而PSO-GPR模型和GPR模型的精度明显低于IPSO-GPR。
4 结论
本文主要研究了暖通空调中AHU送风温度的预测问题,高精度的送风温度预测可以使模型预测控制(MPC)在降低AHU能耗问题中给出更准确的控制优化。利用混沌自适应策略和交叉策略的PSO算法,精确的搜索GPR模型的最佳超参数,使送风温度预测模型的误差低于0.05。此时,MPC在对AHU系统进行控制优化时,给出的控制指令会更加精准,节能效果和房间舒适度会更加理想。
参考文献
[1]SHEA R P, KISSOCK K, SELVACANABADY A. Reducing university air handling unit energy usage through controls-based energy efficiency measures[J]. Energy and Buildings, 2019, 194(JUL.):105-112.
[2]OGAWA Y, SHIRAISHI Y. Multi-objective optimization of energy saving and thermal comfort in thermo active building system based on model predictive control[C]// 40th AIVC-8th TightVent-6th Venticool Conference-Ghent. Belgium, 2019.
[3]GAO F. Quantitative structure-activity analysis of predicted drug targets based on Adaboost-SVM[J]. International Journal of Innovative Computing and Applications, 2020, 11(2/3):109-118.
[4]劉卫校.基于离散灰色预测模型与人工神经网络混合智能模型的时尚销售预测[J].计算机应用,2016,36(12):3378-3384.
[5]ANDREW K, ANOOP V, WEI X P. A data-mining approach to predict influent quality[J]. Environmental Monitoring and Assessment,2013,185(3): 2197-2210.
[6]LIU M M, LIU Z H, ZHOU D, et al. Recognition method of typical anomalies during karst tunnel construction using GPR attributes and Gaussian processes[J/OL]. Arabian Journal of Geosciences,2020,13(16). https://doi.org/10.1007/s12517-020-05782-0.
[7]BERGSTRA J, BENGIO Y. Random search for hyper-parameter optimization[J]. Journal of Machine Learning Research, 2012, 13(1):281-305.
[8]JIANG Y, HU T, HUANG C C, et al. An improved particle swarm optimization algorithm[J]. Advanced Materials Research, 2009, 195-196(1):1060-1065.
[9]YAO B, YU B, HU P, et al. An improved particle swarm optimization for carton heterogeneous vehicle routing problem with a collection depot[J]. Annals of Operations Research, 2016, 242(2):303-320.
[10] 王曙燕,溫春琰,孙家泽.基于自适应粒子群优化算法的测试数据扩增方法[J].计算机应用,2016,36(9):2492-2496.
[11] GE B, LUO H B. Image encryption application of chaotic sequences incorporating quantum keys[J].International Journal of Automation and Computing, 2020, 17(1):123-138.
[12] CHEN B, Efficient communication over additive white gaussian noise and intersymbol interference channels using chaotic sequences[R]. RLE Technical Report,1996,598.
[13] ALAA K F, MHAIBES H I. A low-cost true random bits generator based on chaotic system and light nature[J]. International Journal of Applied Engineering Research, 2018, 13(5):2141-2146.
[14] 徐占洋,郑克长.云计算下基于改进遗传算法的聚类融合算法[J].计算机应用,2018,38(2):458-463.
[15] SAPOUNTZOGLOU N, LAGO J, RAISON B. Fault diagnosis in low voltage smart distribution grids using gradient boosting trees[J]. Electric Power Systems Research, 2020, 182:106254.
[16] NASRUDDIN S, SATRIO P. Optimization of HVAC system energy consumption in a building using artificial neural network and multi-objective genetic algorithm[J]. Sustainable Energy Technologies and Assessments,2019,35:48-57.
[17] GUO J, CHEN F, XU C. Traffic flow forecasting for road tunnel using PSO-GPR algorithm with combined kernel function[J]. Mathematical Problems in Engineering, 2017(8):1-10.
Prediction Model of HVAC Supply Air Temperature Based on IPSO-GPR
KOU Teng-yue, YU Zhong-qing, YANG Xi-xin
(School of Data Science and Software Engineering,Qingdao University,Qingdao 266071,China)
Abstract: Aiming at the characteristics of multi-dimensional, heterogeneous, and non-linear in AHU system, a Gaussian Process Regression (IPSO-GPR) algorithm based on improved particle swarm was proposed. In the traditional PSO algorithm, chaos sequence and crossover strategy are introduced, so that the particles can adaptively adjust the search direction and speed during the movement process, and focus on the area near the local optimal solution to reduce the risk of PSO falling into the local optimal solution. The combined GPR of square index and quadratic rational kernel function is used to deal with the complex AHU nonlinear system. Compared with the PSO-GPR method, the supply air temperature error predicted by IPSO-GPR model is less than 0.07 ℉, and this method achieves a more accurate prediction effect than the PSO-GPR model .
Keywords:
hyperparameter optimization; particle swarm optimization; Chaotic sequences; Gaussian process regression; HVAC supply air temperature

