乐器识别中频谱特征与聚合策略性能评估
赵庆磊 邵峰晶 孙仁诚 隋毅





摘要:乐器识别领域中,传统降采样或全局映射方法得到的特征对输入表达不够准确且判别能力不足。为此借鉴图像领域聚合局部特征的思想,提出一种结合频谱特征和图像领域特征聚合策略的方法。考虑涉及中国传统乐器的研究较少,建立了包含12种中国传统乐器的独奏音乐数据集。为适应频谱图输入,对ResNet34的变体网络模型进行了修改,在建立的数据集上分别针对乐器识别和验证任务对不同特征和聚合策略的9种组合模型进行了性能对比。实验结果表明,基于短时幅度谱和GhostVLAD的组合模型,在乐器识别任务中达到93.3%的准确率,优于其他模型,且收敛速度最快。
关键词:中国传统乐器;乐器识别;卷积神经网络;特征聚合策略;性能评估
中图分类号:J62;TP183
文献标志码:A
收稿日期:2020-12-04
基金项目:
国家自然科学基金青年基金(批准号:41706198)资助。
通信作者:
孙仁诚,男,博士,教授,主要研究方向为大数据分析。E-mail: qdsunstar@163.com
随着深度学习理论的发展,深度学习方法在图像、音频、视频等处理和分析中得到广泛应用。乐器识别(musical instrument recognition,MIR)作为音乐信息检索和音乐数据分析的一部分,是获得音乐信号高级信息的关键任务[1]。准确的乐器识别可以使许多相关任务受益。例如,获得乐器类型可以辅助生成音乐播放列表,声音场景分类,体育音频分类等[2-4]。在过去的几十年里,乐器识别任务的问题之一就是为给定的识别任务选择最佳的特征。何蓉等[5-6]通过对音乐文件使用短时傅里叶转换和梅尔变换生成对应频谱图,对音乐中的乐器等信息进行识别,分别搭建出了符合用户偏好的音乐推荐系统和基于频谱图的音乐流派分类模型。Yu等[7]从音乐中提取梅尔频谱图、梅尔频率倒谱系数(MFCC)和其他五种特征,基于乐器的发作类型和家族构建了带有辅助分类的乐器识别模型。Ashwini等[8-9]分别通过从建立的新颖印度和波斯音乐数据集中提取MFCC等多种特征,实现对多种印度和波斯乐器的识别。王飞等[10]利用从不同类型的乐器中提取的听觉谱图,提出了基于改进卷积神经网络与听觉谱图的乐器识别模型。在识别任务中,不仅特征提取是关键,特征聚合策略的应用也颇为重要。早期的研究主要包括平均池化和最大池化,对邻域内的特征点求平均或取最大,在保持图像不变性的同时减少特征和参数数量。而Lin等[11]基于平均池化提出全局平均池化,将特征图中所有的像素值相加之后求平均,得到一个可以表示对应特征图的数值,通常用于替换分类器中的全连接层。最近的图像领域研究中,Arandjelovi等[12]提出NetVLAD结构,将传统的局部聚合向量(VLAD)结构嵌入到CNN网络中,使得网络可以更加有效地利用特征,提高对同类别图像的表达能力和针对分类任务的区分能力。而Zhong等[13]在此基础上进一步提出GhostVLAD结构,帮助神经网络丢弃对最终分类结果贡献度较小,即鉴别性不足的特征,大幅改进了基于图像集合的识别方法。尽管最近几年在乐器识别方面进行了许多研究,但大多数研究对从音乐中提取的特征直接进行降采样或全局映射,聚合得到的特征往往对输入的表达不够准确且判别能力不足。同时现有研究大多针对西方乐器,对中国传统乐器的研究相对较少。本文借鉴图像领域聚合局部特征的思想,提出了将音乐频谱特征与图像领域的特征聚合策略组合使用的方法,在新建立的中国传统乐器音乐数据集上,与使用传统聚合策略的方法进行对比实验,使用准确率、收敛速度和等错误率对模型性能进行对比讨论模型的性能差异,包括特征和聚合策略本身的影响以及不同类型乐器的影响。
1 模型方法介绍
本文建立了针对乐器识别任务且可以扩展到乐器验证任务的CNN模型,模型使用从原始音乐片段直接提取的频谱图进行训练,而无需对音乐数据进行其他预处理(例如,消除静音、声音活动检测等)。首先使用CNN网络从音乐数据中提取帧级频谱特征,然后基于应用于图像领域的特征聚合策略对提取到的局部特征进行聚合,以获得对输入表达更加准确和鉴别性更强的乐器嵌入,提高识别和验证任务的准确率,最后对整个模型进行端到端训练。
1.1 输入特征
尽管将原始音乐信号用作网络的输入可以减少对专业音乐知识和预处理技术的依赖,但是经过提取的特征可以提高识别精度[14]。本文分别考虑了将音乐数据经过短时傅里葉变换、梅尔变换得到的对应频谱图和MFCC作为整个网络的输入特征。
(1) 短时幅度谱,对经过短时傅里叶变换获得的音频特征求幅值得到的幅度频谱图。假设音乐信号为x(t),其短时傅里叶变换(STFT)[6]为
STFTx(τ,ω)=∫∞-∞w(t-τ)x(t)e-jωtdt(1)
其中,x(t)代表音乐信号;w(t)代表窗函数,通常是以0为中心的汉明窗函数(Hamming Function),τ和ω分别代表时间和频率指数。
(2) 梅尔频谱,输入音乐数据在梅尔标度频率上的幅度频谱图。梅尔标度(Mel scale)[15]是一种基于人类听觉感知定义的非线性频率标度。梅尔频谱图是通过对短时傅里叶频谱图的频率轴应用非线性变换,将普通的频率标度转化成梅尔标度获得的。将普通频率f转换为梅尔频率的公式[16]为
Mel(f)=2595log101+f700(2)
(3) MFCC[17],一种广泛用于自动语音和说话者识别以及自动音乐识别的特征,是在梅尔频率上获得的频率倒谱系数,简称MFCC。
1.2 网络结构
ResNet[18]网络结构已经被证明对于多种视觉任务(例如,图像识别、目标检测和图像分割)和听觉任务(例如,说话人识别、音乐流派分类和乐器识别)非常有效。ResNet网络与标准的多层CNN类似,但是其由残差单元块组成,使用残差连接[19]学习输入和输出之间的映射,使得各网络层可以将残差添加到通道输出的身份映射中。这种方法消除了身份映射时梯度消失的问题,为梯度通过网络提供了清晰的途径。
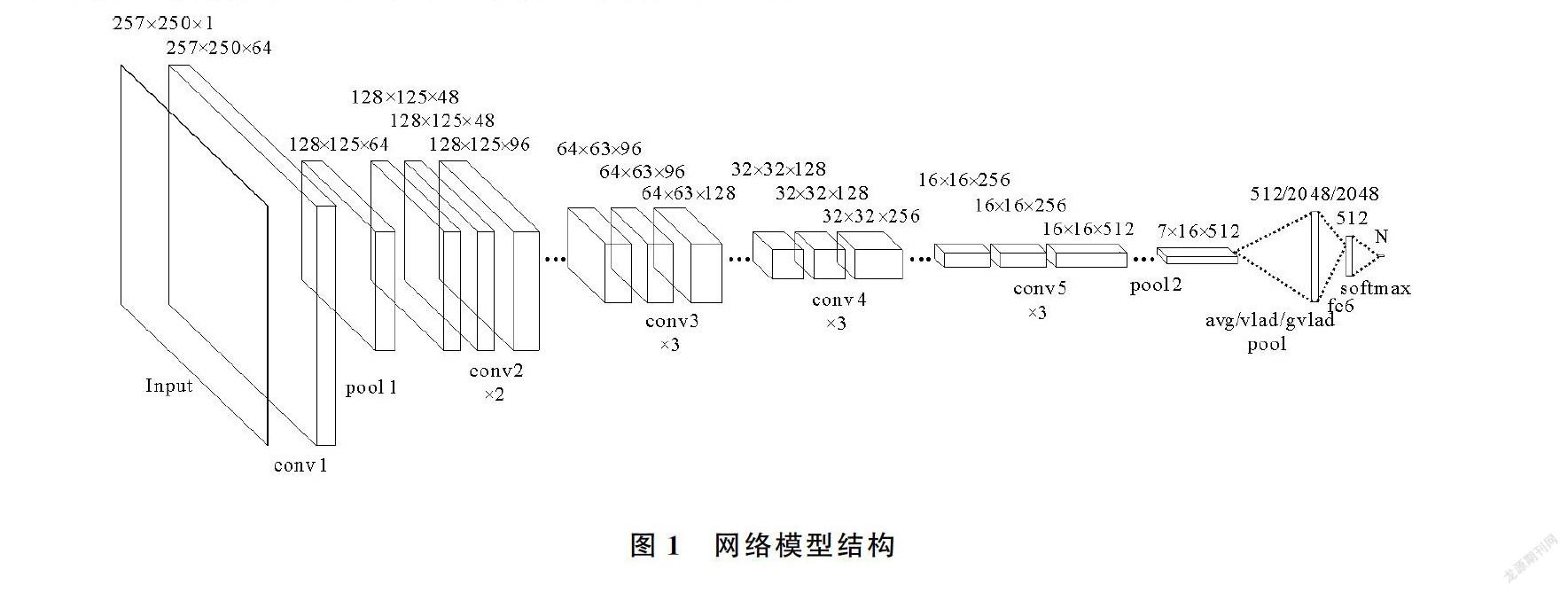
本文使用包含更少网络参数的ResNet34变体网络来进行所有的實验,将原始ResNet34网络中包含2个3×3卷积核的残差单元块替换为包含2个1×1和1个3×3卷积核的残差单元块,并根据频谱图输入的需要对网络层进行修改。最终的网络模型结构如图1所示。
1.3 特征聚合策略
聚合策略在由数据特征驱动的CNN训练中起着重要的作用,负责对网络层提取的特征进行聚合,以获得音频级别的乐器嵌入。本文尝试了三种聚合策略网络层:全局平均池化层,基于NetVLAD层的可训练的聚合层,以及基于NetVLAD层改进的GhostVLAD聚合层。
(1) 平均池化聚合。对于网络层输出的每一个通道的特征图的所有像素计算一个平均值。在聚合特征时,沿时间轴的全局平均池化层可以使得网络对于时间位置具有不变性,这对于属于时序数据的音频数据而言是理想的。此外,全局平均池化层还使得经过聚合后的输出特征与原始的完全连接层的输出特征具有相同的尺寸,同时也减少了网络中的参数数量,避免模型出现过拟合现象。
(2) NetVLAD聚合。CNN网络结构将输入频谱图映射到帧级别的输出特征,并经过降采样处理得到T×D局部特征图。然后,NetVLAD层将其作为输入并产生一个K×D维的全局特征矩阵V,其中K代表所选择的簇的数量,D代表每个簇的维数。全局特征矩阵V[12]
V(k,j)=∑Tt=1ewTkxt+bk∑Kk'=1ewTk'xt+bk'xt(j)-ck(j)(3)
其中,wk,bk和ck是可训练的参数;wk和bk分别代表滤波器和偏置;xt(j)和ck(j)分别代表第t个局部特征和第k个聚类中心的第j个特征值,k∈K,j∈D。式(3)中第一项对应于聚类类别k的输入向量xt的软分配权重,第二项计算向量xt与聚类中心ck之间的残差。然后对全局特征矩阵V中的每一行,即每个簇的残差进行L2归一化,最后通过将该矩阵展平为长向量(即将行向量进行串联)来获得最终输出。为了保持较低的计算和内存要求,使用全连接层进行降维,输出维度为512。
(3) GhostVLAD聚合。GhostVLAD聚合层基于NetVLAD聚合层进行改进,使某些被聚类到一起的簇不包含在最终的串联长向量中,因此这些簇不会对最终的输出表示有所影响,被称为“幽灵簇(ghost clusters)”(使用1个)。由于在对帧级特征进行聚合时,音频片段中嘈杂和不理想的部分,以及对最终结果贡献较小的特征的大部分权重已经分配给了“幽灵簇”,因此对正常VLAD簇和最终结果的影响将有效降低。
2 实验设置
2.1 概述/实验流程图
基于CNN进行特征和聚合策略性能评估的训练和测试框架如图2所示。在训练时的每个轮次中,经过所有批次的训练数据训练后学习到的网络权重,用于计算模型在训练数据集上的分类分数和准确率。然后,在经过所有轮次的训练之后,对于乐器识别任务,训练后的模型用于预测测试数据的类别,并根据预测类别与真实类别计算得到测试准确率。而对于乐器验证任务,训练后的模型用于提取成对测试数据的特征嵌入,并计算它们之间的余弦相似度,作为测试数据对的输出分数,最终再经过计算得到模型在测试数据集上的EER。
2.2 数据集及评价指标
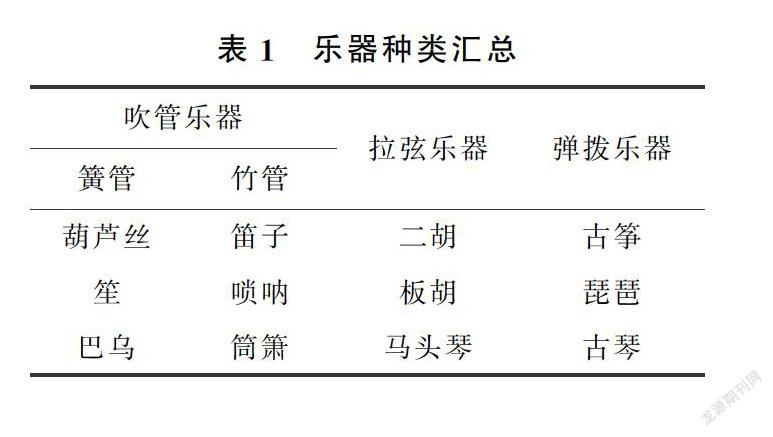
2.2.1 数据集 通过收集整理得到包含12种中国传统乐器的137首音乐数据,每种乐器平均有11首乐曲,根据发作类型可分为吹管、拉弦和弹拨乐器。其中吹管乐器根据乐器材质又分为簧管和竹管。乐器种类如表1所示。
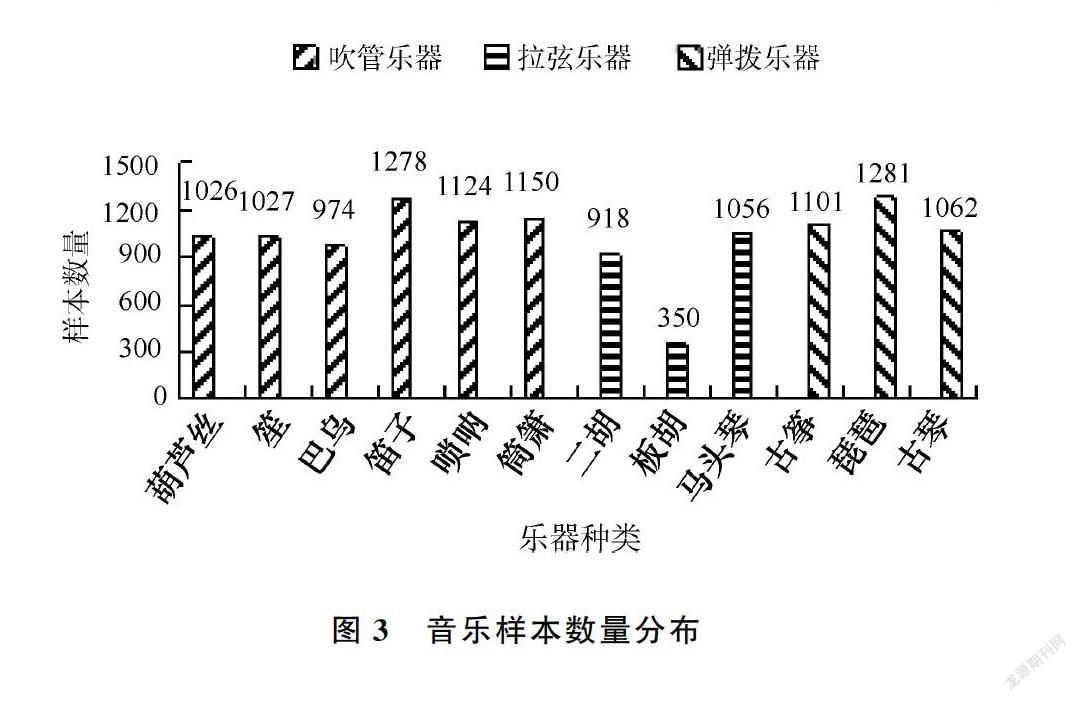
收集到的音乐数据为采样率44.1 kHz,16 bit单声道的数字信号,总时长约为10小时。根据模型和实验需要,以3 s的单位时间长度对原始音乐数据进行平均切割,得到12 347个样本,其中每首乐曲的平均样本数量为90。各种乐器的音乐样本数量分布如图3所示。
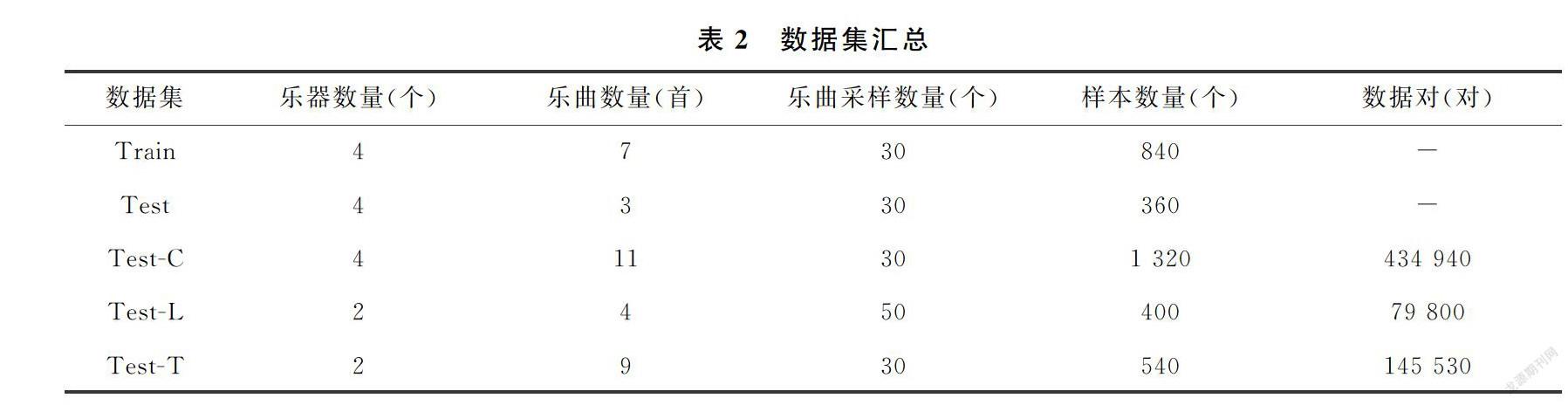
根据音乐样本的乐器种类和数量分布情况以及实际任务需要,对原始音乐数据进行划分,得到训练集(Train)和用于乐器识别任务的测试集(Test),以及用于乐器验证任务的3个测试集。其中训练集和乐器识别任务测试集由多个音乐样本组成,而用于乐器验证任务的测试集是由音乐样本组合而来的数据对组成。数据集汇总如表2所示。
训练集和乐器识别任务测试集:根据乐器识别任务的需要,对涉及3种发作类型的4种中国传统乐器:葫芦丝、笛子、二胡和古筝的音乐数据进行随机采样。由于不同乐器中最少的乐曲数量为10首,每首乐曲中最少的样本数量为30。因此实验从每种乐器音乐数据中选择10首乐曲,并从每首乐曲中随机采样30个音乐样本,按照7∶3的比例制作训练集和测试集,最终从4种乐器的音乐数据中采样得到840和360个音乐样本,分别作为训练集和乐器识别任务的测试集。
乐器验证任务测试集:根据乐器发作类型,并考虑到不同乐器中的最少乐曲数量以及每首乐曲中的最少样本数量,分别对训练集和乐器识别任务测试集之外的8种乐器音乐数据进行随机采样。然后根据乐器验证任务的需要,对采样得到的音乐样本进行组合,最终得到分别包括434 940对、79 800对和145 530对具有相同发作类型乐器音乐数据对的3个测试集:吹管乐器测试集(Test-C)、拉弦乐器测试集(Test-L)和弹拨乐器测试集(Test-T)。
2.2.2 评价指标 不同特征和聚合策略组合下的模型通过准确率(Accuracy)和等错误率(EER)进行评估。Accuracy用于衡量模型识别乐器的准确程度,是被预测为正确类别的样本数占总预测样本数的百分比
Accuracy=TP+TNTP+FN+TN+FP(4)
其中,TP(True Positive)代表真实标签为正例,预测标签也为正例的样本个数;TN(True Negative)代表真实标签为正例,预测标签却为负例的样本个数;FP(False Positive)代表真实标签为负例,预测标签却为正例的样本个数;FN(False Negative)代表真实标签为负例,预测标签也为负例的样本个数。
EER用于衡量模型验证乐器的准确程度,是错误拒绝率(FR,False Rejection)等于错误接受率(FA,False Acceptance),即FR=FA时的值。其中FR代表在真实标签为正例的样本中预测标签为负例的样本数所占的百分比;FA代表在真实标签为负例的样本中预测标签为正例的样本数所占的百分比。
2.3 实验环境和设置
本文所用机器的开发环境为Windows10(64位)操作系统,内存32.00GB;Inter(R)Xeon(R)W-2133处理器;显卡为 NVIDIA GeForce GTX 1080Ti,显存11GB。基于Python3.6.5在Anaconda3中的Spyder3.3平台下进行实验,实验结果的可视化处理由tensorboard、matplotlib库实现。
训练过程中,从每个音乐样本中随机采样,根据使用的输入特征,对音乐样本执行相应的变换,得到相当于2.5秒时间长度的257×250(频率×时间)固定大小的頻谱图,并通过减去均值并除以单个时间步长中所有频率分量的标准差来进行标准化,最后作为输入对模型进行训练。使用标准的softmax损失,初始学习率为0.01的Adam优化器,并设置每个批次的大小为64,在每10个轮次之后将学习率降低10倍。由于考虑的所有模型在经过20个轮次的训练后都趋于收敛,因此只对20个训练轮次内的模型进行性能评估。
3 实验结果分析
将不同特征和聚合策略进行组合并与softmax损失函数以及修改后的ResNet34变体网络架构一起使用,在训练数据集上进行训练,分别在乐器识别测试集和乐器验证任务的不同测试集上进行测试。将针对乐器识别任务的测试准确率和收敛速度,以及乐器验证任务的测试EER对模型性能进行对比。
对于输入特征,短时幅度谱能够保留音频数据中的大部分信息,但往往也会保留对最终识别结果贡献较小的特征信息。梅尔频谱削弱了以摩擦音和其他突发噪声为主的高频细节,因此会丢失一部分特征信息[20]。而MFCC虽然保留了音频的基本特征,但也破坏了一部分有用的特征信息[21]。
对于聚合策略,平均池化策略可以有效降低特征的维度,将特征聚合到一起,但是无法像NetVLAD聚合策略一样根据特征信息的特点更加有效地聚合特征。而GhostVLAD聚合策略在保留大量原始特征信息的同时,往往能够过滤掉许多噪声或贡献度较小的特征信息[22]。
3.1 乐器识别准确率对比
针对乐器识别任务,不同组合下的模型准确率对比如表3所示。其中stft、mel和mfcc分别代表短时幅度谱、梅尔频谱和梅尔频谱倒谱系数,avg、vlad和gvlad分别代表全局平均池化、NetVLAD和GhostVLAD聚合策略。实验中获得最高准确率的是stft-gvlad组合下的模型,该模型使用短时幅度谱作为输入特征,采用GhostVLAD聚合特征,在训练数据集上训练后,验证数据集上的准确率为93.2%。可知,对于使用短时幅度谱作为输入特征的模型,由于短时幅度谱保留了绝大部分的特征信息,并且训练后的GhostVLAD聚合层比全局平均池化层更加有效地对特征进行聚合,相对于NetVLAD聚合策略,可以在聚合特征的过程中过滤掉短时幅度谱本身存在的对识别结果贡献度较小甚至会产生负面影响的特征信息,因此stft-gvlad组合下的模型在验证集上的准确率最高。
对于使用梅尔频谱作为输入特征的模型,由于NetVLAD聚合策略可以将梅尔频谱中符合人耳听觉特点的特征信息比平均池化策略更加有效的聚合起来,且不会像GhostVLAD聚合策略一样损失掉部分有用的特征,因此mel-vlad组合模型在梅尔频谱模型中的准确率最高,在所有的模型中准确率对于使用MFCC作为输入特征的模型,由于MFCC在梅尔频谱的基础上丢失了一部分特征信息,使用GhostVLAD聚合策略会过滤掉更多的特征信息,因此mfcc-gvlad组合模型在验证集上的准确率最低。
3.2 乐器识别收敛速度对比
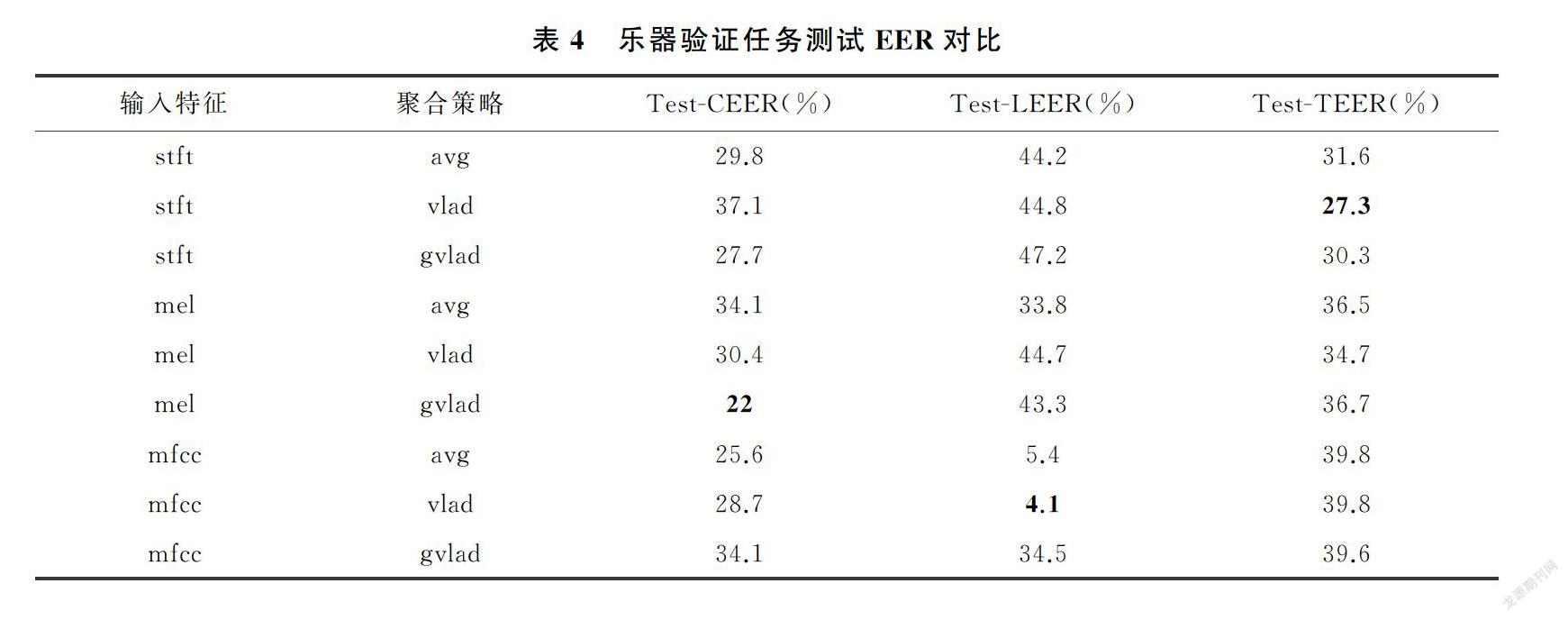
根据不同组合下的模型在乐器识别测试集上实现最高准确率所需的最少训练轮次来定义收敛速度,当比较不同组合下模型的收敛速度时,观察到与上一部分类似的结果。不同模型的收敛速度比较如表4所示。在考虑的所有模型中,stft-gvlad组合下的模型表现出最快的收敛速度,训练轮次为14。
对于不同的输入特征,实验观察到两种不同的收敛速度模式。使用短时幅度谱作为输入特征的模型与使用梅尔频谱和MFCC特征的模型相比,收敛速度更快,收敛所需的平均轮次为16。对于不同的聚合策略,当模型使用GhostVLAD聚合策略时,能够获得比使用全局平均池化和NetVLAD聚合策略更快的收敛速度,平均训练轮次为15。
3.3 乐器验证测试EER对比
针对乐器验证任务,不同组合下的模型在不同测试集上的EER对比见表4。当在不同的测试数据集上进行评估时,模型表现出不同的性能。当在吹管乐器音乐构成的Test-C数据集上进行测试时,使用梅尔频谱作为输入特征,并使用GhostVLAD聚合策略对特征进行聚合的模型表现最好,EER为22%。当使用拉弦乐器音乐构成的Test-L测试数据集时,使用MFCC特征和NetVLAD聚合策略的模型EER为4.1%,在所有的模型中表现最佳。当在弹拨乐器音乐测试数据集Test-T上进行测试时,使用短时幅度谱特征和NetVLAD聚合策略的模型表现最好,EER为27.3%。由于特定的输入特征和聚合策略的组合,以上实验能够从特定发作类型的乐器音乐中获得更多的有效特征,因此得到比其他模型更佳的EER。
综上所述,将频谱特征与图像领域的聚合策略组合使用的模型能够获得更高的乐器识别准确率,并且收敛速度更快,验证了该方法的有效性。同时特定的组合模型在特定类型乐器的音乐上能够获得更佳的乐器验证EER,表明不同的组合模型对于特定类型乐器的音乐具有一定的偏好性。
4 结论
针对乐器识别领域中特征聚合方式简单且涉及中国传统乐器音乐较少的问题,提出了一种将乐器识别中常用的频谱特征与图像领域的聚合策略进行组合的方法,并应用到ResNet34变体网络中。在新建立的中国传统乐器音乐数据集上,针对乐器识别和验证任务将所提出的方法与传统方法进行了对比实验和结果分析。实验结果表明,该方法可以获得对输入表达更加准确和更具判别能力的特征,从而提升乐器识别的准确率以及降低乐器验证的等错误率。后续研究将继续优化特征和聚合策略组合的方法,进一步提升其在乐器识别任务中的性能,并将其更广泛地应用到其他音乐相关领域。
参考文献
[1]DATTA A K, SOLANKI S S, SENGUPTA R, et al. Automatic musical Instrument recognition[M]. Berlin: Springer Singapore, 2017.
[2]AUCOUTURIER J J, PACHET F. Scaling up music playlist generation[C]// Proceedings IEEE International Conference on Multimedia and Expo. IEEE, 2002.
[3]MA L, MILINER B, SMITH D. Acoustic environment classification[J]. ACM Transactions on Speech and Language Processing, 2006, 3(2):1-22.
[4]XIONG Z, RADHAKRISHNAN R, DIVAKARAN A, et al. Comparing MFCC and MPEG-7 audio features for feature extraction, maximum likelihood HMM and entropic prior HMM for sports audio classification[C]// 2003 IEEE International Conference on Acoustics. Hong Kong, 2003: 628-631.
[5]何蓉. 基于卷积神经网络的音乐推荐系统[D]. 南京:南京邮电大学, 2019.
[6]黄琦星. 基于卷积神经网络的音乐流派分类模型研究[D].长春:吉林大学,2019.
[7]YU D, DUAN H, FANG J, et al. Predominant instrument recognition based on deep neural network with auxiliary classification[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2020, 28:852-861.
[8]ASHWINI, VIJAYA K V. Feature selection for Indian instrument recognition using SVM classifier[C]// 2020 International Conference on Intelligent Engineering and Management, ICIEM, 2020: 277-280.
[9]MOUSAVI S M H, PRASATH V B S. Persian classical music instrument recognition (PCMIR) using a novel Persian music database[C]// 9th International Conference on Computer and Knowledge Engineering, (ICCKE). Ferdowsi Univ Mashhad, 2019: 122-130.
[10] 王飞,于凤芹.基于改进卷积神经网络与听觉谱图的乐器识别[J].计算机工程,2019,45(1):199-205.
[11] LIN M, CHEN Q, YAN S C. Network in network[J]. Computer Science, 2013: arXiv:1312.4400.
[12] ARANDJELOVI R, GRONAT P, TORII A, et al. NetVLAD: CNN architecture for weakly supervised place recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(6): 1437-1451.
[13] ZHONG Y J, ARANDJELOVI R, ZISSERMAN A. GhostVLAD for set-based face recognition[C]// 14th Asian Conference on Computer Vision (ACCV). Perth, 2018, 11362:35-50.
[14] 李霞,劉征,刘遵仁,等.关于音乐可视化的研究——声音格式到音乐格式的转换[J].青岛大学学报(自然科学版),1997,9(4):68-72.
[15] STEVENS S S. A scale for the measurement of the psychological magnitude pitch[J]. J.acoust.soc.am, 1937, 8(3):185-190.
[16] DENG J D, SIMMERMACHER C, CRANEFIELD S. A study on feature analysis for musical instrument classification[J]. IEEE Transactions on Systems Man & Cybernetics Part B-Cybernetics, 2008, 38(2):429-38.
[17] WANG Y, HAN K, WANG D L. Exploring monaural features for classification—based speech segregation[J]. IEEE Transactions on Audio Speech & Language Processing, 2013, 21(2):270-279.
[18] HE K, ZHANG X, REN S, et al. Deep residual learning for image recognition[C]// 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR).Seattle, 2016,770-778.
[19] SRIVASTAVA R K, GREFF K, SCHMIDHUBER J. Highway networks[J]. Computer Science, 2015, arXiv:1507.06228.
[20] 馬英,张凌飞,冯桂莲.基于“音乐噪声”的修正谱减法算法分析[J].青岛大学学报(自然科学版),2017,30(3):25-28.
[21] 高铭,孙仁诚.基于改进MFCC的说话人特征参数提取算法[J].青岛大学学报(自然科学版),2019,32(1):61-65+73.
[22] NAGRANI A, CHUNG J S, XIE W, et al. Voxceleb: Large-scale speaker verification in the wild[J]. Computer speech and language, 2020, 60(3):101027.1-101027.15.
Performance Evaluation of Spectrum Features and Aggregation Strategies for Musical Instrument Recognition
ZHAO Qing-lei, SHAO Feng-jing, SUN Ren-cheng, SUI Yi
(College of Computer Science and Technology, Qingdao University, Qingdao, 266071, China)
Abstract:In the field of musical instrument recognition, the features, which obtained by traditional down-sampling or global mapping methods, are insufficient for input expression and discriminative ability. For this reason, drawn on the idea of aggregating local features in the image field, a method of combining spectral features and image field feature aggregation strategies is proposed. At the same time, considering that there are few researches involving traditional Chinese musical instruments, a solo music data set containing 12 traditional Chinese musical instruments is established. In order to adapt to the input of the spectrogram, the variant network model of ResNet34 is modified, and the performance of 9 combination models with different features and aggregation strategies in the task of musical instrument recognition and verification tasks on the established datasets is compared. The experimental results show that the model based on the short-term amplitude spectrum and GhostVLAD achieves 93.3% accuracy in the task of musical instrument recognition, which is better than other models and has the fastest convergence speed.
Keywords:
Chinese traditional musical instrument; instrument recognition; convolutional neural network; aggregation strategy; performance evaluation

