双凹料视觉送料系统的仿真计算与偏差分析

龚惠斌 朱秀球 方军华

关键词：双凹料;生克片（沉降片）;视觉送料系统;仿真计算;误差分析

0引言

某公司的一种圆机针生克片产品WY02，需要用到双凹料在冲床上冲压生产，如果双凹料采用固定问距送料且没有送料补偿的话，送料次数累计到一定数量后，薄料位置误差可能累积到较大值导致薄料在产品中的位置发生较大偏移，使得产品不能满足客户需求（根据产品要求，双凹料送料位置偏差在±0.05mm以内）。为此，需采用一种可以检测到厚薄交界线和该交界线到参考线的间距的方法来计算补偿送料。鉴于机器视觉在检测领域应用广泛、具有可实现高精度检测和响应快的特点，本文搭建了视觉送料系统进行测试验证，并且编写程序进行仿真计算。

1视觉送料系统

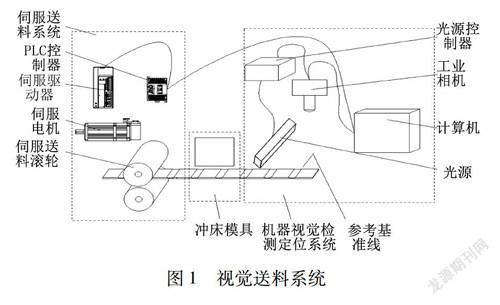
该视觉送料系统主要分成视觉检测系统和伺服送料系统两大部分，详细组件如图1所示。视觉检测系统将检测到的料带与参考线的偏差值发送给伺服送料系统中的PLC，然后PLC中通过计算决定下一次送料的送料距离，并通过发脉冲形式给伺服驱动器，驱动电机运转相应的角度。

2影响因素分析与仿真程序介绍

2.1影响因素分析

通过对双凹料视觉送料系统的分析，可知双凹料视觉送料系统送料偏差的影响因素有以下几种。

（1）料带总段数：如果说送料有累积误差，那么料带总段数越大，则送料偏差越大。

（2）料带的段长：料带段长的误差越大，每次送料的数据相差越大，可能潜在的误差也会越大。

（3）视觉定位处参考线与模具处标准位置之问的料带段數：如果这个段数越多，相当于视觉定位后的送料次数越多，受伺服送料误差的影响将会越大。

（4）送料的标准步距：如果送料的标准步距与实际段长差别较大，可能导致后续的送料偏差。

（5）送料的初始位置：初始位置（初始偏差）的不同可能导致后续的送料偏差不同。

（6）视觉定位误差：直接影响了视觉定位处的厚薄交界线与模具标准位置处的距离计算值，也就影响了送料偏差。

（7）料带的延展性：拉紧状态下和放松状态下的位置偏差，此处暂未考虑。

（8）冲床的振动：问接影响了视觉定位误差，此处也暂未考虑。

2.2仿真程序主要变量

（1）料带总段数m：此处取实际一卷料的料带段数的上限，m=60000。

（2）料带的标准步距I：这里取30.5mm为标准步距（料带段长的标准值），固定不变。

（3）光检处参考基准线与模具标准位置之间料带的段数n。

（4）光检处参考基准线与模具标准位置之间的距离x：此处假设x=lxn。

（5）实际料带段长为以标准步距为平均值的段长x：数组，其公差范围为ProdX。

（6）光检误差系数为ProdD：这里取0.4%（参考文献[1]中光检相对误差的比例0.38%左右）。

（7）送料误差随机数k：根据伺服送料器的送料精度1μm来给出，送料误差范围为0～0.001mm的随机数k。

（8）料带的起始位置t：t的选择一般在-0.5～0.5mm。

（9）厚薄交界线与模具标准位置的送料偏差数组S：数组，为所要求得的偏差分布。

（10）送料段长L：数组，表示每次送料的长度。

（11）T：数组，表示光检处厚薄交界线与参考线的距离，带符号，前正后负。

（12）S：数组，厚薄交界线与模具标准位置的送料偏差。

（13）S：光检处厚薄交界线到模具标准位置的距离。

（14）S：S。的数组，表示各段厚薄交界处到模具标准位置的距离。

（15）S：计算得到的n-1段的长度。

（16）FileHandle：文件句柄，用于记录送料偏差数据，将之保存至文本文档中。

2.3仿真程序

（1）该次送料偏差=前一次送料偏差+该次实际段长-前一次送料步距+前一次的送料误差;

（2）先计算第0段到第n-2段的送料偏差：该n-1段采用的是标准步距送料，送料偏差较大，实际送料偏差分析时，该部分数据剔除考虑。

（3）再计算第n-1段到第m-1段的送料偏差以及视觉定位误差，并将结果保存至文本文档中。

2.4 Halcon程序

3仿真结果及分析

通过改变其中一个变量，固定其他变量的方法来进行仿真对比试验，在不考虑冲床振动和料带延展性的情况下，得到仿真结果如图2～7所示。

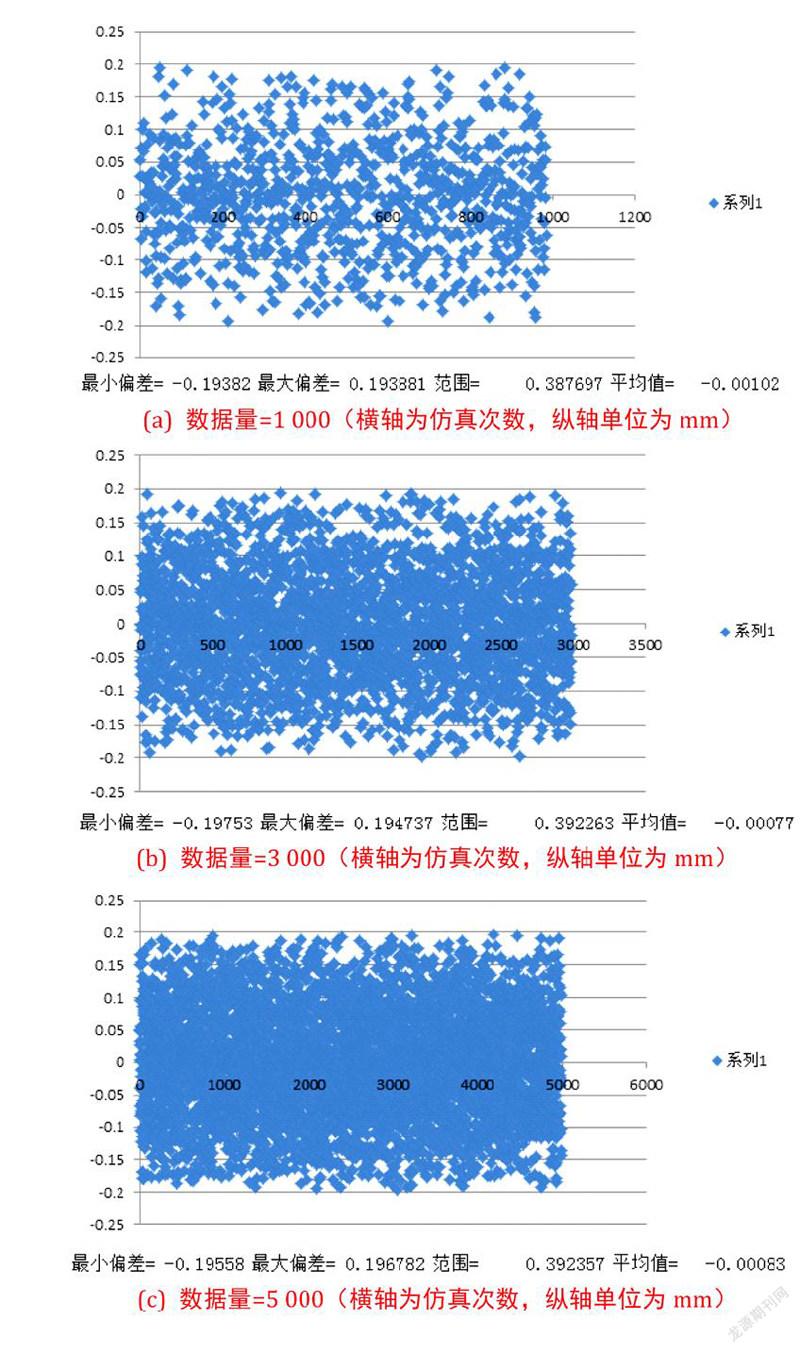
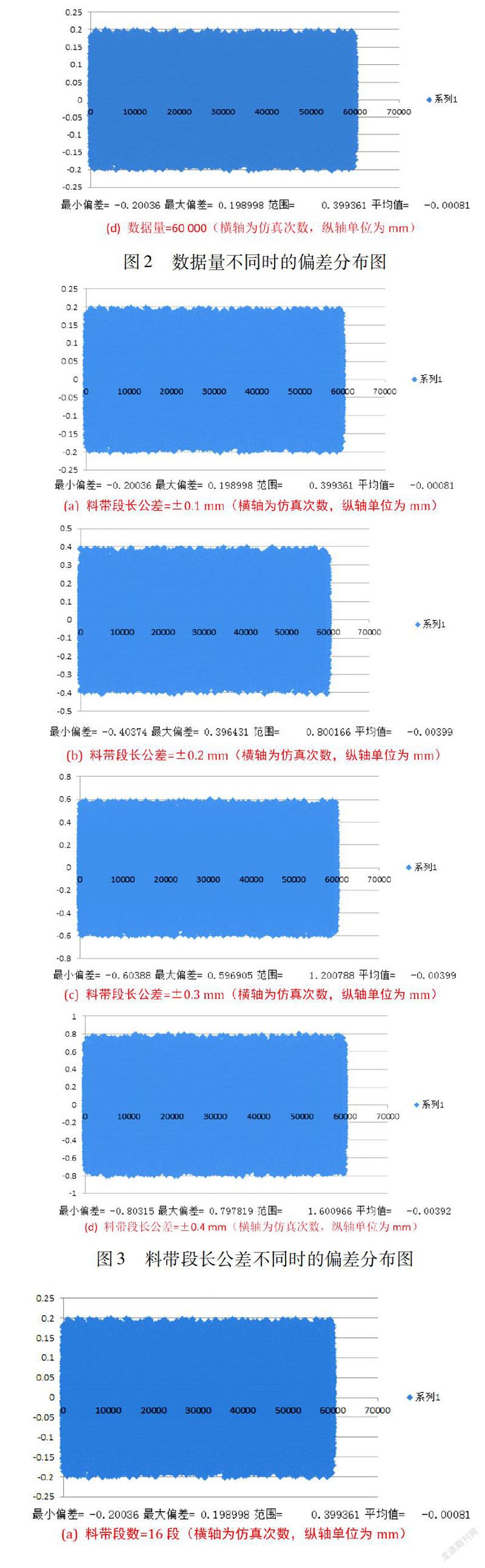
从图2的偏差分布图来看，对于段数等于16、标准段长等于30.5mm、公差范围等于±0.1mm的材料和初始送料位置偏差为0的情况下，无论仿真数据多少组（小到上千组，大到数万组），偏差的分布总是基本上在-0.2～0.2mm平均分布。

从图3的偏差分布图来看，对于段数等于16、标准步距等于30.5mm、初始送料位置偏差为0的情况下，料带段长的公差范围越大，导致送料偏差范围越大，而且几乎成2倍关系。

从图4的偏差分布图来看，对于标准段长30.5mm、公差范围在±0.1mm的材料来说，无论段数是几段还是几十段，偏差的分布总是基本上在-0.2～0.2mm平均分布，随着段数的增加到上百段到数百段，偏差分布的平均值逐渐向负值偏移。对于冲床上安装的距离来说，段数基本在5～20段以内，偏差的分布范围一般在-0.2～0.2mm，因此，段数对送料偏差的影响微小。

从图5的偏差分布图来看，标准段长设置偏小，会导致偏差分布的平均值变负值;标准段长设置偏大，会导致偏差分布的平均值变正值;设置值越是偏大或偏小，偏差分布的平均值的绝对值会越大;不过小范围内的偏差±0.4mm以内时，偏差分布偏移小于0.04mm。

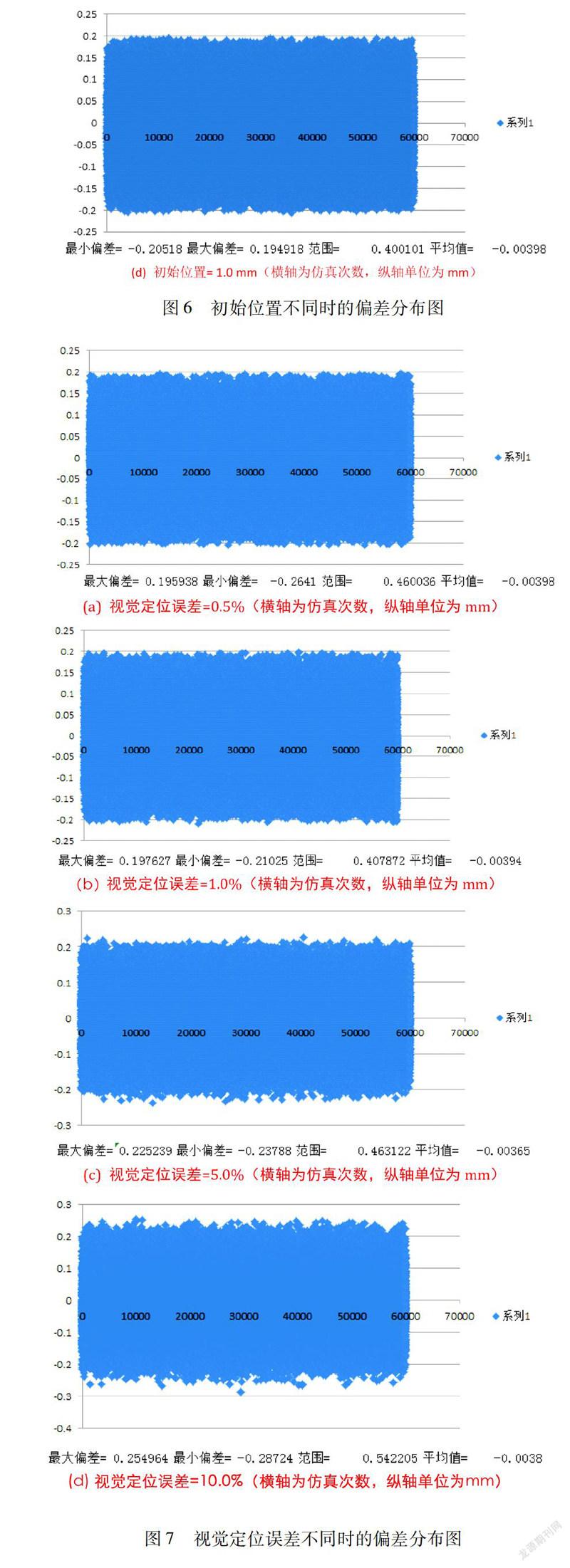
从图6的偏差分布图来看，初始送料位置偏差与模具标准位置的距离不同，对后续偏差分布的影响很小。

从图7的偏差分布图来看，视觉定位误差对最终偏差分布的影响也不大，定位误差虽然大幅度从0.5%上升到10%，但是偏差平均值几乎不变，偏差范围略微增大（从±0.2mm变成±0.25mm左右）。

4结束语

通过对仿真计算的结果进行分析，本文得出了这样一个结果，在保证视觉送料正常稳定的前提下，送料偏差在偏差范围内基本呈现均匀分布状态，送料偏差范围受料带自身的段长公差范围的影响很大，成两倍关系，送料偏差受段数、标准步距偏大或偏小的影响相对微小，送料偏差不受材料总段数和料带初始位置偏差的影响，送料偏差受视觉定位误差的影响较小。该仿真程序及其仿真结果分析的试验，为产品该项品质的控制和设备生产调试提供了依据。