多元表征让算理算法直观显现

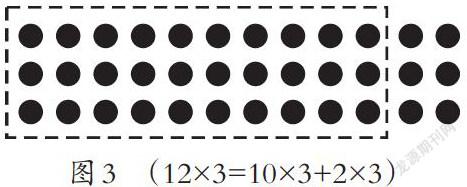
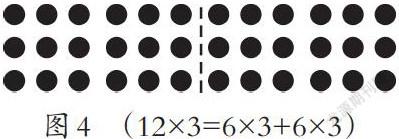
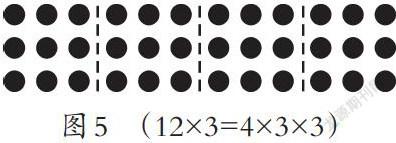
【摘要】本文论述在小学数学课堂教学中运用多元表征呈现算理的策略，提出动作表征、图形表征、语言表征和符号表征等四种教学方式，让学生经历由直观算理到抽象算法过渡和演变的过程，突破教学的重难点。

【关键词】小学数学 多元表征 算理 算法

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2021）09-0130-02

所谓数学多元表征，是指将数学学习对象进行心理多元认知编码并与之建立对应、建构意义联系的过程。新课标明确指出：“教师要根据学生的认知规律，引导学生进行有效的数学学习。”在数学学习领域，绝大部分学习对象都可以用实物情境、教具模型、图表、言语、书写符号等五种类型来表征，由此可见，数学多元表征，可以多维度建构算理，多层次抽象计算过程，多视角归纳计算方法，让算理算法“看得见”。

在探究计算题时，需要运用多元表征对算理进行解释，让学生从多角度深入理解算理，通过多元化的表征方式，从不同的角度解释算理，易于挖掘计算的核心，呈现算理，建构计算过程，凸显计算的本质属性。在小学数学低年段计算教学中，学生在探究计算算理和算法的过程中有四种表征方式，即动作表征、图形表征、图表表征和符号表征。如何帮助学生充分利用多元表征理解算理、掌握算法，这是笔者一直思考的问题。现根据自己在低年段计算教学中的实践，谈谈思考和体会。

一、动作表征，让学生经历操作的过程，探究算理

根据教育心理学理论，在小学数学教学中，学生多感官的参与有利于数学知识的学习。在多元表征中，所谓动作表征，就是指学生通过动手操作挖掘数学知识的本质，构建数学模型的一种方式。数学计算具有抽象性，学生容易只关注算法，漠视算理，久而久之就变成“只知其然，不知其所以然”，只会简单、机械地计算，导致只要题目有稍许变化，他们就无法理解和掌握。然而，正确理解算理是归纳算法的前提和基础，因此，教师要提供充分的自主操作的机会，让学生通过动手操作深入探究计算的本质，真正理解算理，掌握基本的数学知识和数学技能，积累丰富的数学活动经验。

如在教学北师大版一年级上册《9加几》时，学生根据题意列出算式9+5，但不会计算，这是学生遇到的新困难。教学时，教师要引导学生探究9加几的算理，并归纳出计算方法，而这正是教学的重点所在。为了帮助学生真正理解算理，从而归纳出计算方法，笔者引导学生分小组合作学习，让学生借助事先准备的学具（小棒、计数器）尝试计算9+5。学生通过摆小棒、拨计数器这些动作表征，得出不同的发现：有的学生发现左边摆9根小棒，右边摆5根小棒，合起来就是14根小棒;有的学生从5根小棒中拿出1根小棒放到左边，与9根合在一起是10根，右边还有4根，10+4=14;有的学生是利用计数器拨珠子，先在个位拨9，再一颗一颗地拨5颗，当个位10颗珠子拨满了，就把个位的10颗换成在十位拨1颗，继续在个位拨余下的4颗，得14颗，等等。通过这样的动作表征，学生能自主发现并理解9+5的算理，再引导学生将刚才的過程用简单的数学语言归纳出算法，实现了本节课的预设目标，有效地突破教学的重点和难点，培养学生借助学具自主学习的能力。

又如在教学北师大版三年级上册《两位数乘一位数口算》这部分内容时，教材呈现了一幅主题图。（如图1所示）

学生在理解题意后列出算式：12×3。本节课的教学重点是让学生理解“将12分成10+2，再相乘”的过程，并且能够理解将算式分为“10×3”和“2×3”计算的算理，归纳“两位数乘一位数”的计算方法。如何才能突破这个教学难点，实现本节课的教学目标呢？笔者设计了小组合作动手操作环节：让学生摆小棒进行操作，通过摆小棒帮助计算12×3，明白其中的算理。

学生先摆3个10，拿出3捆，表示3个10，即3×10=30;再拿出3个2根表示3×2=6;把两部分合在一起30+6=36。这种摆小棒的过程，通过动作表征将算理直观地呈现（如图2）。在这个教学环节，教师通过小组合作的形式，让学生动手摆小棒，形象地呈现“3个10+3个2”的过程，让学生深刻地理解“两位数乘一位数”的计算算理。一个小小的操作帮助学生深刻地理解了这一乘法计算的本质。通过动作表征，为学生接下来学习“多位数乘一位数”打下了良好的算理基础。

二、图表表征，将抽象内容具体化、直观化，培养学生的数形结合思想

所谓图表表征，是指学生利用已有的知识经验，将文字内容在脑中“画图表”，用画线段图、示意图、表格等形式表现出来。在小学数学教学中，有效地运用图表表征，可以帮助学生理解算理，使学生学会学习，实现过程性目标。

如在教学北师大版三年级上册《两位数乘一位数的口算》例题“计算12×3”时，当学生通过操作表征初步感知“分别用十位和个位的数与3相乘，再将两个积合起来”进行计算之后，笔者设计在小组合作中提供点子图给学生圈一圈，让他们通过圈图，直观地呈现“10×3+2×3”的算理，通过图表表征经历直观形象的算理到抽象算法的演变过程。

方法一：（如图3）学生通过圈图不难发现：12=10+2，左边10×3=30，右边2×3=6，左右两部分合起来是30+6=36。归纳得出算法：分别用十位的数与个位的数乘第二个乘数，再把两次相乘的积合起来。

方法二：（如图4）12=6+6，先将12分成2个6，用虚线分隔成左右两部分，每个部分的点子数都是6×3，是我们的表内乘法，就可以算得出6×3=18，左右两部分都是18，18+18=36。

方法三：（如图5）12=3×4，将12分成4个3，每部分点子数都是3×3=9，有4个9，9×4=36。

方法四：（如图6）也可以用表格帮助计算，将12分成10+2，分别与3相乘，填在相应的表格里，再将两个积相加。

学生用圈图形和画表格分析算理，表述方式呈现多样化。学生已经有了图表表征的经验，此时就可以很快得出两位数乘一位数的算理，梳理出两位数乘一位数正确的算法。

在这个教学环节中，教师由浅入深、由基础知识到数学的本质，一步一步深入，引导学生通过图表表征解析，让学生充分经历一个从抽象到形象的过程，不但掌握了“两位数乘一位数”的算理，而且培养了学生的数感。

三、符号表征，让学生经历抽象的过程，归纳算法

《义务教育数学课程标准（2011年版）》提出：“教师要培养学生理解并运用符号表示数、数量关系和变化规律的能力，帮助学生运用数学符号进行数学表达和数学思考。”在小学数学教学中，数学符号表征具有准确性、抽象性和规律性的特点，能够充分体现数学学习的特性。因此，教师要引导学生学会运用数学符号，经历简约抽象的数学表征过程，揭示数学规律。

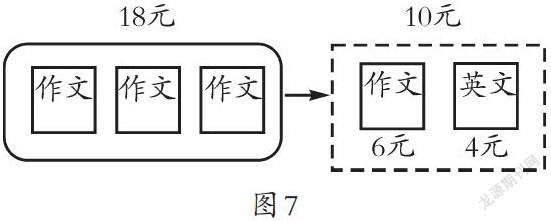
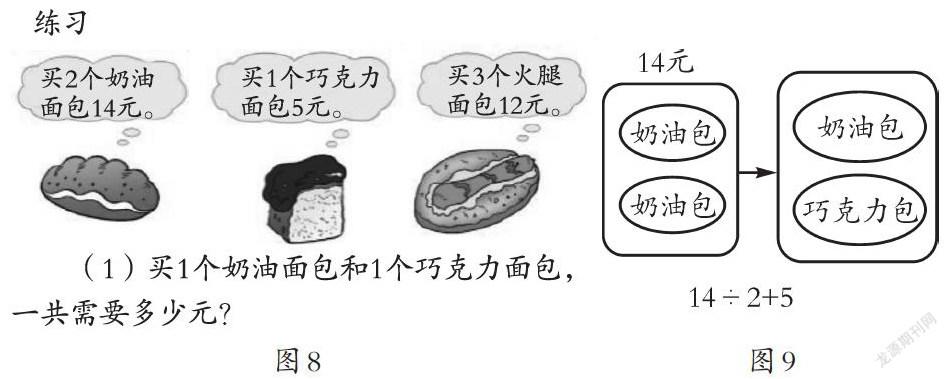
例如，在教学“除加除减混合运算”时，为了让学生自己理解运算顺序的算理，在学生找出题中数学信息和问题后，笔者请学生说出计算时需要先算“一本作文本多少元”，再算“笑笑买一本作文本、一本英语本需要多少元”。为了让学生进一步理解运算顺序，笔者引导学生用数学符号表示题意。（如图7）

在这个教学环节，利用符号表征“买3本作文本18元”可以先用18÷3=6（元）求出1本作文本6元，再用6+4=10元就能求出“笑笑买一本作文本、一本英语本需要10元”。用简单的符号，清晰地呈现出“有除法又有加法要先算除法再算加法”的运算顺序，进一步反映了思维的有序性。

学生在完成上面的练习题时也采用符号表征呈现运算顺序，他们根据数学符号变化，直接提炼出计算顺序：有除法又有加法要先算除法再算加法，让数学运算顺序的归纳自然而然、水到渠成。

四、語言表征，让朗朗上口的语言帮助学生掌握计算方法

语言表征重在“说”，将计算算理转化为朗朗上口的、合理的、可理解的语言，帮助学生掌握计算方法，促进学生计算能力的发展，同时训练学生的思维更加灵活多样，强化学生的数学表达能力。

如北师大版一年级《9加几》一课，在学生经历9+5的算理探究、归纳算法时，笔者引导学生归纳出算理：看大数9，分小数5，9和1凑成十，加剩下的4是14。通过这样朗朗上口的口诀帮助学生理解算理，牢固掌握算法，提升学生的计算能力。又如，在教学用计数器帮助计算时，让学生边拨计数器，边说出算理。如9+5，个位先拨9，9和1凑成十，个位满十，向十位进1，个位再拨4，9+5=9+1+4=14。在学生经历了实物的直观，逐步发展到语言的直观，由基于语言的表述描述来代替基于动作和形象的演示，可以帮助学生快速理解算理、熟练算法，提高效率。

总之，数学表征从内容上反映了数学学习对象信息的部分，但从形式上看是丰富的、互补的、变通的，合理运用数学多元表征，借助多元表征学习，能够让学生充分经历由直观算理到抽象算法的过渡，进而突破数学学习的难点，学会从数学的角度观察、发现、分析算理，归纳算法，从而让算理算法“看得见”。

【作者简介】秦虹（1974— ），女，广西桂林人，硕士研究生学历，一级教师，主要研究方向为小学数学教学，目前研究课题是培养小学低年级学生运算能力的实践研究。

（责编 林 剑）