含裂纹内啮合变位齿轮的疲劳性能研究

梁兴波

摘要：针对内啮合变位齿轮，裂纹是影响齿轮传动系统的主要因素。建立内啮合变位齿轮的动力学模型，得出内啮合变位齿轮的接触啮合力，并对虚拟样机进行有限元分析，结果表明，应力最大值点位于接触侧的齿根圆位置。在此基础上，运用联合软件分析的方法，对内啮合变位齿轮的裂纹疲劳分析。

关键词：变位齿轮;裂纹;啮合力;联合软件分析法

中图分类号：U463.3                                       文献标识码：A                                文章编号：1674-957X（2021）06-0001-03

0  引言

齿轮传动广泛用于各重工和制造行业[1]，同时常被用作减速器、增速器、差速器和换向机构以及其它特殊用途，是世界各国机械传动发展的重点[2]。但是它也有存在自身的一定缺陷，那就是齿轮疲劳，其中疲劳断齿所占比例最大。特别是出现裂纹之后，对疲劳寿命和接触啮合都有很大的影响，对整体的效应也会有影响。然而疲劳断裂不会发生明显的塑性变形，相对比较难检测和预防，这是影响齿轮传动效率以及造成经济损失的重要因素。

针对含裂纹内啮合变位齿轮疲劳性能的研究，为工程检查和评估提供依据参考，也有利于提高它的可靠性和寿命，大大提高工作效益。

1  內啮合变位齿轮模型建立

内啮合变位齿轮的主要参数如表1所示。

三环传动主要采用内啮合角度变位齿轮，所以要建立内齿板和外齿轮的模型就需要运用变位齿轮的构建方法。

在笛卡尔坐标系下，变位齿轮的齿廓曲线参数方程为：

在式（1）和式（5）中，db为基圆直径;theta为压力角由0到45°。

建立第一条变位齿轮的齿廓曲线，第二条变位齿轮的齿廓曲线通过创建基准面，再镜像生成，最后拉伸实体。对于外齿轮和内齿板的构建轮齿是不一样的，内齿板采用切除法构建轮齿。

2  内啮合变位齿轮动力学分析

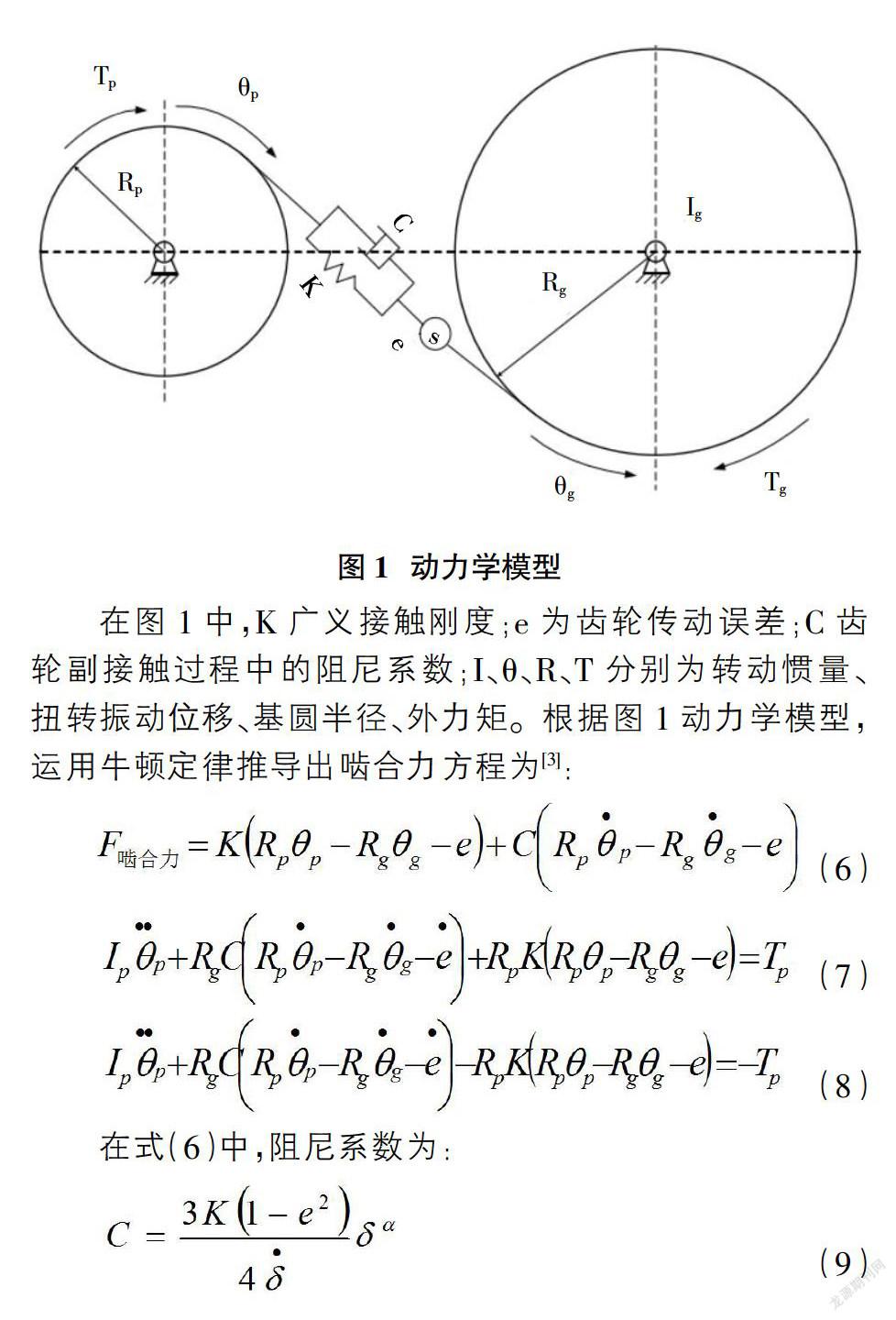
根据内啮合齿轮副的力学模型并结合齿轮动力学模型，创建本文内啮合变位齿轮的动力学模型，模型如图1所示。

在图1中，K广义接触刚度;e为齿轮传动误差;C齿轮副接触过程中的阻尼系数;I、？兹、R、T分别为转动惯量、扭转振动位移、基圆半径、外力矩。根据图1动力学模型，运用牛顿定律推导出啮合力方程为[3]：

动力学模型建立之后，运用MATLAB函数编程求解出啮合力，并进行对比分析。分析结果如图2所示。

从图2中可以看出啮合力在-600～600N之间，最大啮合力出现在波动幅值上方，为600N，当机构运动到波动幅值下方时。

3  内啮合变位齿轮有限元分析

因为内齿板和外齿轮接触啮合时齿轮工作情况是一样的，有限元分析效果也是一样的，所以选择两对啮合齿轮进行有限元分析。采用六面体网格划分，175179个节点。

根据齿轮的工作状态，对外齿板的轴孔内圈加固定约束，给外齿轮输入扭矩T，扭矩T为：

从图3中可以看出内齿板应力分布，最小应力为87.581Pa，最大应力为168.44×108Pa。最大应力和最小应力的差值比较大，主要是因为齿轮接触啮合部分受力比较大，其他部分受力比较小。最大应力出现主要是在齿根位置和接触啮合点，齿根位置的应力要比接触啮合点应力大，而且位于接触侧。

4  含裂纹内啮合变位齿轮寿命分析

对内齿板裂纹疲劳寿命分析时，将运用ABAQUS软件和FRANC3D软件联合运用分析法[4-6]，主要分析步骤如下：

4.1 对内齿板定义子模型

进裂纹分析时，首先是导入*.inp格式的模型，选择导入并划分为全局模型和子模型;分别输出子模型和全局模型的有限元模型，生成两个*.inp文件，用于后续的裂纹扩展分析。

4.2 在子模型中添加初始裂纹

首先建立裂纹，选择裂纹类型为椭圆形裂纹。其次定义裂纹的尺寸，椭圆裂纹的长轴半径a=1mm，椭圆裂纹的短轴半径b=0.25mm。再次就是定义椭圆形裂纹坐标为（73.5018，3.091，-20），围绕X、Y、Z轴在各旋转90°。最后再重新划分网格，为了保证计算精度，裂纹处的网格会自动加密。

4.3 求解应力强度因子

通过计算机计算出相关参数和应力强度因子，如图4～图6所示。

图4中，从图中可以看出，应力强度因子KI是呈现对称性，裂纹尖端的中部应力强度因子要比边缘位置的大;应力强度因子KI在边缘的变化趋势要比中部大，说明边缘的扩展速度要比中部大;节点0处的应力强度因子要比节点1处小一点，出现这种情况主要因为裂纹中部拉应力比较大。通过查相关的手册，可以找到相关材料的KIC。45号钢的KIC=281MPa，FRANC3D分析结果最大应力强度因子KI=13.6MPa，KI<KIC，所以满足要求，符合断裂准则。

在图5中，应力强度因子KII在节点0.2处和节点0.8处出现负值，负值是代表扩展方向为反方向。应力强度因子KII也是呈现对称性，节点0处附近的应力强度因子大于节点1处;裂纹尖端边缘是正方向扩展，裂纹尖端节点0.2处和节点0.8处是反方向扩展;虽然裂纹尖端节点0.2处和节点0.8处是反方向扩展，但是相比裂纹尖端边缘扩展速度，中部还是很小。这些也是因为II型应力在裂纹尖端边缘位置要大于裂纹尖端中部。

从图6中可以看出应力强度因子KIII近似一条直线，是以节点0.5处为界，左半部分是正方向扩展，右半部分是反方向扩展，扩展速度相近，1.89MPa为最大应力强度因子。节点0.5处应力强度因子KIII为零，说明节点0.5处III型裂纹是不扩展的。

求解出应力强度因子之后，下文将根据应力强度因子，判断主要裂纹类型，并对主要裂纹类型进行裂纹扩展分析。

4.4 裂纹扩展分析

根据上一节计算出的应力强度因子，对应力强度因子分析中发现KI的结果最大，比II型和III型应力强度因子要大很多。所以裂纹主要是I型裂纹为主，裂纹一开始扩展就发生比较严重的产生张开位移，但也有一点滑开位移。根据应力强度因子已经判断裂纹主要模式是I型为主，II型和III型为辅。

裂纹判断完成之后，开始裂纹扩展分析。裂纹扩展第一步设置最大周向应力准则，第二步添加材料相关Paris参数。第三步设置扩展增量为0.2mm，最后进行裂纹扩展。

裂纹开始扩展第一次之后，FRANC3D会自动对子模型进行裂纹识别并对裂纹子模型进行网格划分，网格划分之后;将进行第二次裂纹扩展，求出裂纹尖端的应力强度因子;第二次裂纹扩展完成之后，FRANC3D自动会网格划分，再进行第三次裂纹扩展。这样一个重复过程一直到断裂状态，或者设置自动扩展时到达到设置的终止条件为止。

4.5 疲劳裂纹寿命分析

第一次扩展完成之后，再进行应力强度因子求解，根据应力强度因子进行第二次裂纹扩展，这样一个反复循环的过程，直到实现断裂。这样一个循环过程，可以得出应力强度因子历程曲线数据，在利用FRANC3D的后处理模块可得出裂纹扩展寿命曲线。计算出的裂纹疲劳扩展寿命结果如图7所示。

从图7中可以看出，隨着裂纹扩展不断的增加，寿命次数也在逐渐增加，当裂纹扩展到8.37mm时，整个过程裂纹扩展了41次，出现断裂，最终寿命次数为36891次。通过对三环传动的传动齿轮进行寿命预测，将扩张裂纹长度8.37mm带入公式中：

综合上文分析发现，对内齿板进行疲劳寿命分析是运用联合软件分析，很大程度上弥补各自的不足，分析结果合理、可行。出现裂纹之后，寿命急剧下降为36891次，说明裂纹对寿命影响还是很大。

5  结论

从内齿板应力分布中看出，最大应力为168.44×108Pa。最大应力出现主要是在齿根位置和接触啮合点，齿根位置的应力要比接触啮合点应力大，而且位于接触侧。

三环传动的疲劳寿命分析，结果表明，扩张裂纹长度8.37mm，最终寿命次数为36891次，寿命次数大幅度降低。裂纹的主要扩展模式，以张开型裂纹为主，以滑开型裂纹和撕开型裂纹为辅。

参考文献：

[1]李秀.三环减速器齿轮参数化建模及其接触应力有限元分析[D].辽宁：辽宁科技大学，2014：1-3.

[2]饶振纲.行星传动机构设计[M].北京：国防工业出版社，1994：22-25.

[3]石珍.少齿差行星减速器多参量藕合非线性振动特性研究[D].重庆：重庆大学，2015：20-21.

[4]才建.汽车齿轮表面疲劳裂纹扩展机理研究[D].武汉：武汉理工大学，2015.

[5]王延忠，田志敏，侯良威.航空重载面齿轮三维裂纹分析与疲劳寿命预测[J].北京航空航天大学学报，2014，40（02）：148-153.

[6]尹土邦.基于载荷谱的航空发动机传动齿轮疲劳寿命研究[D].沈阳：沈阳航空航天大学，2012.