考虑频繁换道倾向的交通流元胞自动机模型

赵林涛， 尚 平， 冷军强

(1.哈尔滨工业大学 交通科学与工程学院， 哈尔滨 150090； 2.陕西省公安厅交通管理局， 西安 710061； 3.哈尔滨工业大学(威海) 汽车工程学院， 山东 威海 264209)

交通流在宏观层面呈现出复杂特征，其根源在于车辆之间复杂的相互作用，在多车道交通流中，换道是一类基本操作。随着换道研究的逐渐深入，交通工程学者已建立诸多微观模型[1]，但关于换道倾向对交通流定量影响的相关研究仍有不足。通过对换道倾向可能产生的影响进行研究，可实现对高速公路车辆进行及时信息诱导，有效提升交通运行效率。

在换道对交通流影响研究方面，Jin[2]引入换道强度变量修正基本图方法，分析了交织区车辆换道对交通瓶颈的影响；Suh等[3]基于实测数据，分析了交通拥堵时车辆换道对时走时停波的影响；何磊[4]建立信号交叉口通行能力折减系数模型和行车延误模型，分析了交叉口违规换道对交通效率影响。在研究方法方面，元胞自动机CA(Cellular Automaton)由于规则简单、灵活可调、易于编程等优点[5]，近年来在交通流研究，尤其是车辆微观仿真领域应用广泛。Ye等[6]考虑网联车运行特性，建立异质交通流元胞自动机模型，分析了网联车不同渗透率对道路通行能力影响；Pang等[7]建立考虑雨天驾驶行为的双车道元胞自动机模型，分析了不同降雨强度下交通事故影响；Zeng等[8]建立考虑停车行为影响的双车道元胞自动机模型，分析了出租车与公交车停靠站不同组合下交通流特征。

整体而言，目前研究多集中于车道流率、车道变换次数等宏观变量对交通运行效率的影响，而针对车辆驾驶行为倾向，特别是特殊驾驶行为倾向对交通运行效率影响的相关研究较少。为此，本文通过对车辆轨迹数据进行统计分析，以研究车辆速度、车头间距对换道倾向影响，改进换道概率函数刻画上述影响，并分析驾驶员屡次被超车后其驾驶行为变化情况，提出驾驶行为变化倾向函数。基于上述函数改进车辆换道规则，构建基于该换道规则的双车道元胞自动机模型。

1 数据分析

本文选取NGSIM中I-80路段[9]车辆轨迹数据进行分析，基于Python语言对自由流时段CSV文件进行提取处理。数据包含16:00—16:15时段内共2 052辆机动车的1 262 678帧信息，其中换道车辆670辆，总换道次数1 043次。为进一步研究车辆速度、车头间距对驾驶员换道的影响，统计车辆换道前最后一帧信息，分析车辆速度、车头间距与路段车辆换道次数间的规律，结果如表1、图1所示。

利用统计软件SPSS对分类变量换道次数进行样本T检验，结果表明：1) 在95%的置信区间下，换道4次与换道≤3次速度差异不明显的假设被拒绝，即样本数据提供显著证据表明2个样本中速度差异明显；在95%的置信区间下，换道5次与换道≤3次车头间距差异不明显的假设被拒绝，即样本数据提供显著证据表明2个样本中车头间距差异明显。2) 换道时刻速度与换道倾向正相关，车头间距与换道倾向负相关。即换道前车辆平均速度越高，车头间距越小，车辆换道概率越大，换道前车辆平均速度越低，车头间距越大，车辆换道该辆车越小。

表1 不同换道次数车辆速度、车头间距信息

图1 车头间距、速度与单位长度内车辆换道次数关系

2 模型构建

2.1 跟驰规则

NaSch模型通过简单的规则模拟车辆跟驰状态，一定程度上可以反映实际交通状况，但无法再现交通流中亚稳态、回滞等复杂现象。为更准确描述交通流状态，本文的跟驰规则采用夏运达等[10]的改进VDR模型，模型将路段拆分为N个长度为l的元胞，元胞有2个状态：0和1，分别代表未被车辆占用和被车辆占用，每辆车车速为0，1，2，…，Vmax，Vmax为最大车速，从时间t→t+1过程中，模型按照如下规则演化：

1) 确定下一时刻车辆随机慢化概率P与减速幅度ΔV

(1)

(2)

2) 加速

V(i,t+1)=min{V(i,t)+1,Vmax}

(3)

3) 减速

V(i,t+1)=min{V(i,t+1),d(i,t)}

(4)

4) 依概率P随机慢化

V(i,t+1)=max{V(i,t+1)-ΔV,0}

(5)

5) 位置更新

X(i,t+1)=X(i,t)+V(i,t+1)

(6)

式中：V(i,t)表示第i辆车在t时刻的速度，cells/s；X(i,t)表示第i辆车在t时刻的位置；d(i,t)表示第i辆车在t时刻行驶方向前未被占用的元胞数量；P0、P1、a0、a1、a2、Vmax均为常数。

但是要保证以下2点：1)P0>P1，保证车辆本时刻状态为静止时，下一时刻车辆随机慢化概率高；当车辆本时刻状态为运动时，下一时刻车辆随机慢化概率低；2)a1>a2=a0，当本车车速高于前车车速，车辆为避免追尾碰撞而保证减速度较大；当本车车速低于前车车速，车辆不必有驾驶行为担忧，因此减速度较小。

2.2 换道规则

考虑车辆频繁换道特性，经典STCA模型的保守换道规则不再适用。因为一方面驾驶员频繁换道时，凭借自身车辆与相邻车道后方车辆的相对速度来判断换道可能性，若自身车速较高，即使与目标车道后方车辆间距很小，仍有可能采取换道行为。另一方面，频繁换道会对驾驶员产生心理干扰，干扰结果表现为：少部分驾驶员因不满屡次被超车，从而跟随前车进行频繁换道；一部分驾驶员对自己驾驶技术产生怀疑，从而保守驾驶，转变为道路中的慢车；其余内心坚定的驾驶员则保持当前行驶状态。

通过上述分析，本文定义驾驶行为变化倾向函数Sn，并改进换道概率函数Pn,change，优化换道规则，构建考虑频繁换道倾向的双车道元胞自动机模型。模型换道规则如下：

1) 确定车辆类型。

(7)

2) 计算车辆换道概率Pn,change。

(8)

3) 换道条件是否满足

dndn

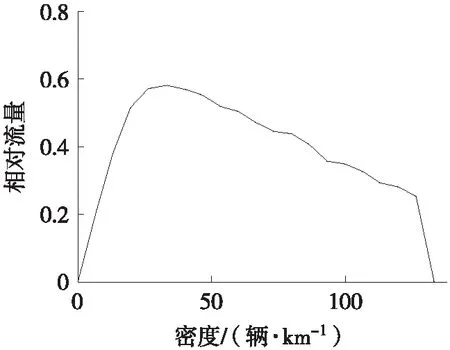
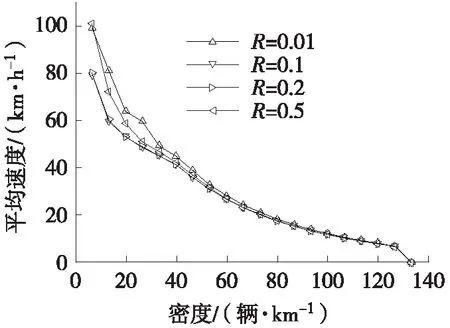
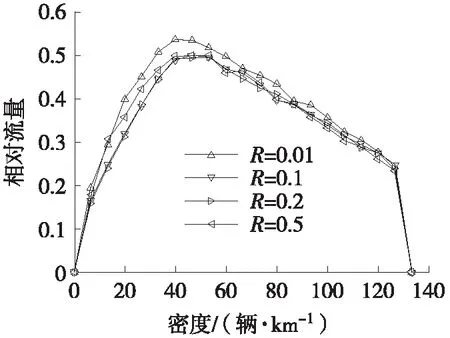
rand()

dn,back>dsafe

(9)

4) 驾驶行为是否转变：普通车辆(Sn=0)在特定n个时步内，累计被频繁换道车辆(Sn=1)超车3次，车辆驾驶行为会以一定概率发生变化。

(10)

式中：Sn=-1,0,1分别表示第n辆车为慢车、普通换道车辆、频繁换道车辆；dn表示第n辆车与本车道前车之间空元胞个数；dn,other表示第n辆车与相邻车道前车之间空元胞个数；dn,back表示第n辆车与相邻车道后车之间空元胞个数；dsafe表示确保不会发生撞车的最小安全距离；Pn,change表示换道概率；Δv为本车速度与前车速度的差值，两车速度差值越大，后车换道概率越大；Δd为车辆与相邻车道前车之间的空元胞数减去车辆与本车道前车之间空元胞数；γ表示频繁换道驾驶员在不同场景自发的换道倾向。

3 模型仿真分析

3.1 模型验证

图2 经典STCA模型流量与密度关系曲线

图3 不同车辆随机慢化率P1下流量与密度关系曲线

3.2 模型对比分析

STCA模型和STCA-FLC模型平均速度、相对流量与密度关系如图4、图5所示。

系统密度ρ∈(0,13)辆/km时，相较于STCA模型，STCA-FLC模型的平均速度、相对流量都有提升，分别约为6.67%和3.02%，主要是此时交通密度较低，频繁换道行为对相邻车道后车影响有限，此时无论车辆是否换道，目标车道后车都可保持期望速度运行。

系统密度ρ∈(13,41)辆/km时，相较于STCA模型，STCA-FLC模型的平均速度、相对流量有所下降，分别约为9.48%、14.91%，此时交通量逼近道路通行能力，车辆仅可实现有限换道，频繁换道行为致使慢车大量生成，慢车是抑制交通运行效率的主要因素，特别是2个慢车并行移动时，可导致系统出现移动堵塞，进而造成平均速度降低、相对流量下降，该现象与实际交通运行特征相符。

系统密度ρ∈(41,120)辆/km时，交通流趋于饱和，车辆换道困难，即换道过程中的安全条件、换道动机与换道概率Pn,change至少有一个条件不满足，STCA-FLC模型近似退化为STCA模型，2条曲线基本重合，与实际相符。

图4 STCA和STCA-FLC模型平均速度与密度关系曲线

图5 STCA和STCA-FLC模型相对流量与密度关系曲线

3.3 初始频繁换道车辆比例影响分析

STCA-FLC模型不同初始频繁换道车辆比例R下平均速度与密度关系如图6所示。由图6可见：1) 各条曲线均再现了交通流速度与密度关系规律，即随着交通流密度增加，车辆平均速度下降，且速度下降幅度减小；2) 系统最大速度vR=0.5>vR=0.01>vR=0.1=vR=0.2。当R= 0.5时，由于频繁换道车辆比例较高，无论交通如何运行，生成的慢车比例远低于快车比例；当R= 0.01时，此时交通密度较低且频繁换道车辆较少，车辆频繁换道并不影响目标车道后车运行，因此生成的慢车更少，对交通的抑制作用远无法抵消频繁换道车辆带来的速度增长；当R= 0.1时，慢车的低速行驶对平均速度抑制作用达到饱和，因此，当R= 0.1与R= 0.2时，曲线基本重合；3) 系统密度ρ∈(8,41)辆/km时，速度下降幅度ΔVR=0.5≥ΔVR=0.01>ΔVR=0.1=ΔVR=0.2。当R= 0.5、0.01时，仿真结束时系统中特殊车辆(频繁换道车辆与慢车)比例较高，由此导致的速度方差偏大，交通系统极不稳定，系统会由于单个参数的变化而产生剧烈波动；当R= 0.1、0.2时，特殊车辆对系统的影响相互抵消，交通系统已经稳定，交通系统不会因单个参数的改变而产生剧烈波动；4) 系统密度ρ∈(41,120)辆/km时，系统开始拥堵，车辆换道行为条件难以满足，频繁换道行为发生概率极低，STCA-FLC模型退化为STCA模型，此时4条曲线基本重合。

图6 不同初始频繁换道车辆比例R下STCA-FLC 模型平均速度与密度关系曲线

STCA-FLC模型不同初始频繁换道车辆比例R下相对流量与密度关系如图7所示。由图7可见：1) 各条曲线均再现了经典交通流理论模型的曲线特征，即随着密度的增加，相对流量先迅速上升至最高值，再缓慢下降；2) 系统密度ρ∈(0,41)辆/km时，相对流量FluxR=0.01≥FluxR=0.5>FluxR=0.1/0.2。以初始频繁换道车辆比例R= 0.5为例，随着车流密度的增加，系统中频繁换道车辆带来的速度提升逐渐被慢车抵消，此时慢车的存在对系统流量起决定性作用，而初始频繁换道车辆比例R= 0.1、0.2情况下，慢车的抑制作用已饱和，因此相对流量FluxR=0.5逐渐向FluxR=0.1/0.2靠拢，并最终重合；3) 系统相对流量最大值FluxR=0.01>FluxR=0.5=FluxR=0.1=FluxR=0.2。相对流量达到最高点意味着慢车对交通系统的抑制作用达到饱和，在初始频繁换道车辆比例R= 0.1时，慢车的抑制作用已达到饱和，因此，系统相对流量最大值不再随R的增大而改变。

图7 不同初始频繁换道车辆比例R下STCA-FLC 模型相对流量与密度关系曲线

4 结论

本文改进了换道概率函数刻画车辆速度、车头间距对换道倾向影响，并定义了驾驶行为倾向函数表征频繁换道对目标车道紧邻后车的影响，通过优化换道规则，构建了考虑频繁换道倾向的双车道元胞自动机(STCA-FLC)模型，分析了频繁换道对交通运行效率影响规律，据此得出以下结论：

1) 车流密度ρ∈(0,13)辆/km时，STCA-FLC模型较STCA模型车辆平均速度、流量分别最大提高约6.67%、3.02%；车流密度ρ∈(13,41)辆/km时，STCA-FLC模型较STCA模型车辆平均速度、流量分别最大降低约9.48%、14.91%。

2) 存在一定比例频繁换道车辆时，交通更为稳定。初始频繁换道车辆比例R= 0.1时，慢车带来的不良影响已饱和，此时系统稳定，不会由于单个因素的改变对整个系统造成巨大影响。

3) 频繁换道行为对交通流的影响并非完全负面。自由流状态下，频繁换道可提高交通运行效率；在自由流向堵塞流转变过程中，频繁换道会抑制车辆平均速度、流量；在堵塞流状态下，频繁换道发生条件难以满足，此时不考虑其对交通效率影响。