基于VMD-GRU和非参数核密度估计的风电功率概率区间预测

王 鑫，李 慧，范新桥，刘思嘉

(北京信息科技大学 自动化学院，北京 100192)

0 引言

风资源的不平稳性和随机性，导致风电并网会造成电网波动，给电网调度带来压力，危害电网安全。风电功率概率区间预测可以提供较为准确的风电功率波动区间，为电网调度提供有效信息[1]。

风电功率概率区间预测的基础是点预测[2]。常用的点预测方法包括：物理方法、统计学方法、人工智能方法以及组合预测方法[3]。物理方法主要是根据风电场的数值天气预报(numerical weather prediction,NWP)信息，通过功率曲线计算得到功率预测值，预测精度受NWP精准度的影响。统计学方法主要有时间序列法、卡尔曼滤波法、支持向量机(support vector machine，SVM)[4]等，这些方法适用于少量数据的研究。人工智能方法[5]有卷积神经网络(convolutional neural network，CNN)、回声状态网络(echo state network，ESN)以及循环神经网络(recurrent neural network，RNN)等，更适用于海量数据的研究。

与点预测目的不同，区间预测是通过一定的方法得到目标的取值区间，而这个区间是由一定置信水平下点预测结果的最大值和最小值组成。利用概率区间预测值可以构造完整的概率密度曲线，以估算风电功率值的可能范围。文献[6]提出一种改进混沌时间序列的风电功率区间预测方法，结合蚁群聚类和SVM对单一预测法加以改进，获得了较好的预测效果。薛阳等[7]提出了一种基于双向长短期记忆神经网络(long short-term memory，LSTM)和Bootstrap法的风电功率概率区间预测方法，该方法强调了数据之间的关联程度对预测精度的影响。除了Bootstrap法以外，分位数回归法[8-9]、NKDE算法[10-11]等都广泛应用于概率区间预测。

为降低原始序列波动性对预测的影响，张亚超等[12]将聚类经验模态分解(ensemble EMD，EEMD)—样本熵和核极限学习机(kernel extreme learning machine，KELM)组合构造预测模型，得到了良好的预测效果。除EEMD外，完备经验模态分解(complete EEMD，CEEMD)、小波分析(wavelet analysis，WA)、变分模态分解(variational mode decomposition，VMD)[13]等也常用来进行风电数据预处理，降低功率序列的不平稳性。

本文将VMD和GRU相结合，构建风电功率点预测模型，得到风电功率的点预测值及误差分布情况；统计并分析误差集，将其划分为多个子区段，采用NKDE算法对不同的子区段分别构建概率区间预测模型，得到概率密度曲线；重组各子区段的预测结果，得到风电功率的概率预测区间；通过仿真实验对比不同核函数和不同窗宽的预测结果，确定出最佳核函数和最优窗宽，并对比区段划分和不划分两种情况下区间预测的效果。

1 变分模态风电功率点预测

1.1 变分模态分解算法

VMD是由Konstantin Dragomiretskiy和Dominique Zosso于2014年提出的一种完全自适应、非递归的信号分解算法，它可以将强波动性的风电功率信号分解成若干个特征、频段互异且带宽有限的子模态(intrinsic mode functions，IMF)序列，记为uk，记ωk为uk的中心频率。对风电功率信号v(t)进行K阶VMD分解，可以看成约束变分问题：

(1)

式中：{uk}={u1,u2,…,uK}为K个IMF分量集合；{ωk}={ω1,ω2,…,ωK}为K个IMF分量中心频率集合；δ代表Dirac分布；*代表卷积因子。

引入二次罚项以及拉格朗日乘子后，得到增广拉格朗日方程如式(2)，于是将式(1)转化为求解式(2)鞍点的问题，即无约束优化问题。

L({uk},{ωk},λ)=

(2)

式中：α为二次惩罚因子；λ为拉格朗日乘子。

常采用乘子交替方法(alternate direction method of multipliers，ADMM)求解式(2)的鞍点。由ADMM算法迭代更新计算uk和ωk：

(3)

(4)

图1 VMD计算步骤

1.2 门控循环单元神经网络

传统RNN在进行大数据量的拟合映射时，容易产生梯度消失和梯度爆炸现象，从而导致预测能力有限。基于深度学习的RNN设置有循环机制和门结构使自身具有记忆功能，弥补了上述问题，从而可以处理不同长度的功率等信号序列，提升预测能力。LSTM[14]和GRU[15]是RNN的两种深度学习模式下的流行变体，LSTM设置有输入门、遗忘门和输出门，GRU在LSTM的基础上进行改进，未设置存储单元，采用更新门代替LSTM网络中的输入门和遗忘门，不但保留了LSTM良好的计算能力，同时在结构上进一步简化，减少了计算时间，其内部结构及单元间连接如图2所示。本文采用GRU网络进行风电功率点预测建模。

图2 GRU结构

图2中，A、B、C分别表示前一时刻、当前时刻和后一时刻的激活单元，r表示重置门，z表示更新门，tanh和σ为激活函数。

σ为Sigmoid函数，值域为(0,1)：

(5)

tanh为双曲正切函数，值域为(-1,1)：

(6)

假设网络单元的输入为xt，隐藏层的输出为ht，则ht可由式(7)～(11)得出。

更新门：zt=σ(Wzhht-1+Wzxxt)

(7)

重置门：rt=σ(Wrhht-1+Wrxxt)

(8)

(9)

(10)

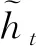
1.3 风电功率点预测实例

本文将VMD分解算法同GRU网络相结合，构建风电功率点预测模型。以我国某风电场采集到的历史实测功率序列作为样本，采样间隔为15 min。

首先，对风电功率序列训练样本集进行VMD分解，统计各子模态IMF的中心频率，确定分解阶次为K=10，将其记为IMF1～IMF10，并计算SE将分解后的IMF分量进行组合，减少建模数量，此时得到3个子序列，记为k1、k2和k3：

(11)

然后，采用GRU分别对重构的子序列k1、k2和k3进行点预测建模。GRU点预测模型的输入层元素为待预测时刻t前的10个功率值，GRU层的激活神经元个数设定为150，全连接层的激活单元数设定为128，激活函数选用ReLU：

(12)

输出层输出为t时刻的功率值。点预测模型的损失函数选用均方误差(mean square error,MSE)：

(13)

最后，将各子序列GRU点预测模型的预测结果叠加，得到最终功率预测值。

为了说明VMD-GRU组合预测方法的有效性，本文采用VMD-BP、VMD-ELM、GRU三种点预测方法与之进行对比，图3为4种点预测模型3天共288个采样点的预测结果。表1为4种方法下归一化平均绝对误差eNMAE和归一化均方根误差eNRMSE的对比。

图3 四种点预测方法的预测结果对比

表1 四种点预测方法的eNMAE和eNRMSE

由表1可知，采用本文方法的eNMAE和eNRMSE分别是3.08%和3.95%，均低于其他3种预测方法。可见本文提出的VMD-GRU点预测方法具有较高的预测精度。

2 风电功率概率区间预测建模

2.1 非参数核密度估计

NKDE算法是由Rosenblatt和Emanuel Parzen提出的一种非参数检验方法，不需要利用有关数据分布的先验知识，对数据分布不附加任何假定，可从数据样本本身获得相应预计时段的分布情况。由于它可以直接估计随机变量的密度，不需要假设分布的优越性，因此，适用于风电功率区间预测研究。NKDE算法的表达式为

(14)

式中：N为样本总数；h>0表示窗宽也称为平滑参数，可任意设定；p为风电功率点预测误差随机变量；pi为功率点预测误差的第i个样本点值；K(·)表示所选用的非负核函数，采用不同的核函数会得到不同的估计结果。

通过NKDE算法，可以得出连续且光滑的累积分布函数(cumulative distribution function，CDF)和概率密度函数(probability density function，PDF)。

窗宽h的设置和核函数K(·)的选取直接影响着NKDE算法中密度曲线的光滑程度以及拟合程度，进而影响计算精度。常用于NKDE算法中的核函数有：高斯核函数(Gaussian)、三角核函数(Triangle)、Epanechnikov核函数等，这3种常用核函数如表2所示。本文将选取这3种核函数进行对比，确定最佳核函数。

表2 三种常用核函数

2.2 概率区间预测建模

本文采用基于VMD-GRU的组合预测方法实现风电功率点预测，得到相应的点预测功率值和预测误差集，再将误差集划分为多个子区段，对不同的子区段分别采用NKDE算法构建概率区间预测模型，得到概率密度曲线，最后将各子区段的预测结果值重组，得到风电功率的概率预测区间，并通过仿真实验对比不同核函数和窗宽下的预测结果，确定最佳核函数和最优窗宽。具体步骤如下：

1)筛选所需的风电场历史数据，构建训练样本集和测试样本集。

2)采用VMD算法对风电功率序列进行分解，设置合适的K值，得到多个特征、频段互异的IMF分量。

3)计算各个IMF分量的样本熵值(sample entropy，SE)，将多个IMF分量重构成新的子序列，记为k序列。

4)采用GRU网络对每一路子序列分别构建点预测模型，得到各个子序列预测结果，再将所有子序列预测模型的预测结果叠加，得到待测功率的点预测值及预测误差值。

5)统计预测误差并划分成多个子区段，对于每个子区段分别采用NKDE算法，构建概率区间预测模型。

6)确定最佳核函数和最优窗宽，得出某置信度下风电功率的概率预测区间分布情况。利用测试集样本数据加以验证。

图4为基于VMD-GRU和NKDE的风电功率概率区间预测框图。

图4 基于VMD-GRU和NKDE的风电功率概率区间预测

2.3 窗宽的计算

在核密度理论中，窗宽h的求取对区间估计结果影响较大。本文采用渐进积分均方误差[16](asymptotic mean integrated square error，AMISE)来计算窗宽hAMISE：

(15)

式中：K(·)表示所选用的核函数；n为样本数。

选取不同的核函数K(·)，窗宽的计算也随之改变。当选取高斯函数为核函数时，窗宽的计算可简化为

hAMISE=1.06σn-1/5

(16)

式中σ为样本的标准差。

2.4 评价指标

常用的概率区间预测评价指标有两个，即覆盖率和平均宽度[17]。预测区间的覆盖率(prediction interval coverage probability，PICP)是用来评价区间预测的可靠性，其值越大越好；预测区间的平均宽度(prediction interval average width，PIAW)是用来考量区间预测的清晰度，其值越小越好。PICP和PIAW分别为：

(17)

(18)

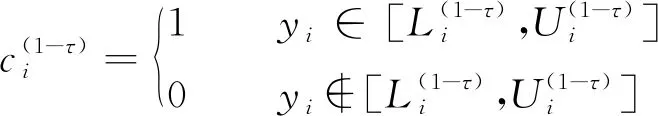
3 算例分析

利用VMD-GRU预测方法得到的预测误差进行概率区间预测研究，对比不同核函数和不同窗宽下的预测结果，确定最佳核函数和最优窗宽。在此基础上，对分区段和不分区段两种情况下，不同置信度时区间预测结果的PICP值进行对比。

对VMD-GRU点预测方法输出结果的预测误差进行统计，发现误差分布在[-0.15,0.17]范围内。为了提升概率区间预测效果，将误差集均等划分成8个子区段，对各子区段进行预测拟合。

选取3天的预测误差进行仿真验证，分别采用高斯核函数、三角核函数和Epanechnikov核函数进行对比，窗宽取h=0.002。表3为85%置信度下3种核函数区间预测PICP和PIAW的计算结果。

表3 三种核函数区间预测PICP和PIAW对比

由表3可知，不同的核函数在同一窗宽下的预测结果差别不大，PICP值均为98.61%，且PIAW值相差也不大，均满足预测要求，但高斯核函数PIAW值最小。因此，将高斯核函数确定为概率区间预测模型的最佳核函数。

表4为采用AMISE方法得到的8个子区段最优窗宽计算值hAMISE。

表4 八个子区段的hAMISE计算值

表5为85%置信度、不同窗宽下的区间预测的PICP和PIAW对比。其中，各子区段的hAMISE窗宽计算值由表4给出。由表5可知，随着窗宽的增大，PICP会有所增加，但是预测区间的PIAW值也会随之增大；在hAMISE窗宽下，PICP值已经达到98.61%，同时预测区间的平均PIAW也最小，因此更适用于风电功率概率区间预测研究，选其为最优窗宽。

表5 85%置信度、不同窗宽下区间预测PICP和PIAW对比

选用高斯核函数和AMISE窗宽，将误差集分8个子区段和不分子区段两种情况下，置信度分别取80%、85%、90%时，对比区间预测的PICP结果如表6所示。

表6 区段划分与不划分情况下的区间预测PICP对比 /%

由表6可知，在同一置信度下，划分子区段预测的区间覆盖率均明显高于不划分区段直接预测的结果；随着置信度的降低，二者的PICP值均会下降，但分区段的PICP值下降幅度较小。比如，在90%置信度下，分区段时的PICP值为99.31%，高于不分区段时的94.79%；当置信度降至80%时，分区段的PICP值仅减少了1.74%，而不分区段的减少了12.15%。由此可见，本文所提出的划分子区段方法得到的区间预测效果更好。图5为选用高斯核函数和AMISE窗宽，置信度为90%、划分8个子区段后建模得到的区间预测结果图。

图5 置信度90%下分区段概率区间预测结果

4 结束语

本文提出一种基于VMD-GRU和NKDE的风电功率概率区间预测方法，它是在VMD-GRU模型得到较为精准的点预测结果基础上，通过构建划分子区段的概率区间预测模型得到未来某时刻风电功率可能值范围，提高了概率区间预测精度，并利用仿真分析确定出适用的最佳核函数和最优窗宽。相比于点预测而言，概率区间预测能够更加有效地刻画出未来时刻风电功率的不确定性和波动区间，从而为电网的调度和安全运行决策提供更多可参考的信息。