基于PCT的飞行体转速提取方法研究

邓 睿，苏 中

(1.北京信息科技大学 高动态导航技术北京市重点实验室，北京 100192；2.北京信息科技大学 现代测控技术教育部重点实验室，北京 100192)

0 引言

随着科技发展，常规武器技术不断提高，对武器系统精度的要求也随之提高，相应地对弹丸复杂运动特征进行解耦得到单一运动特征的精度就有了越来越高的要求。提取瞬态信号一直是数据处理研究中的热门，军工领域对高动态载体测试数据的瞬态信号的提取具有重大工程意义[1]。高动态飞行体要飞行平稳需保持高速旋转，利用其陀螺定向性保证弹头向前稳定飞行，但高动态飞行体的飞行数据超出了陀螺仪的量程精度[2]，这使得对高动态载体运动特征的认知成为当今研究与应用领域的一大难点。

常见的对飞行体运动特征进行分析的研究方法有很多，如过零法、短时傅里叶变换[3](short-time fourier transform，STFT)、极值法、魏格纳-威利分布[4](Wigner-Ville distribution，WVD)、小波变换[5](wavelet transform，WT)、希尔伯特-黄变换[6](Hilbert-Huang transform，HHT)等。算法不同，估计精度不同，适用的信号不同，优缺点也不同。

1947年R.K.Potter 等首次提出了STFT，其核心思想是对时域信号加窗，然后对加窗后的信号做傅里叶变换，对视窗函数做平移，最后得到由一系列频谱组成的二维图像[7]。

但由于STFT的窗函数固定，因此STFT无法保障同时在时域和频域内都达到令人满意的测量精度。WT继承了STFT的视窗函数，但同样无法保障同时在时域和频域内都达到令人满意的测量精度[8]。HHT分析信号时，第一步先对信号进行EMD分解(empirical mode decomposition)，分解结果为IMF(intrinsic mode function)，然后对分解信号进行希尔伯特变换(Hilbert transform，HT)解调，以此获取目标信号的瞬时频率，但是这种算法因为EMD固有的问题而存在一定的缺陷[9]。

杨扬[10]将参数化时频分析方法通过构造与信号匹配的变换核的方式，提出多项式调频小波变换(polynomial chirplet transform，PCT)。因PCT的计算特性，这种算法只能分析有限长度的信号，通过循环逼近估计多项式变换核参数的方法，使变换核参数与信号匹配度更好，时频分析结果集中度更好。因此本文以PCT为核心算法，提取高动态飞行体转速。

1 多项式调频小波变换

参数化时频方法分析非平稳信号会采用可准确逼近信号时频特征的变换核，利用这种方法构造出与信号相匹配的频率旋转算子和平移算子，多项式线性调频小波变换是变换核参数估计方法，这种参数估计方法通过迭代逼近求精，其本质基于频率旋转算子和平移算子的短时傅里叶变换，选择多项式为变换核，信号的频域分辨率更高，对信号的时频特征表示得更准确。在噪声条件下这种方法可以有效确定多项式调频小波变换的变换核参数[11]。

以二阶多项式相位信号为例，信号模型为

(1)

(2)

其中ci(i=1,2,…,n)是多项式的变换核参数。由此可得多项式调频小波变换的公式为

(3)

其中

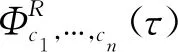
从多项式线性调频小波变换公式可知其本质是采用变换核逼近信号的时频特征，根据Weierstrass逼近定理，在闭区间中任意的、连续的函数均可用多项式级数一致逼近，因此多项式调频小波变换适用于长度有限的非平稳信号，以多项式相位信号为例：

s(t)=sin[2π(10t+5t2/4-t3/6+t4/160)]

t∈[0,15]

(4)

对该信号加入白噪声，时域波形如图1所示。

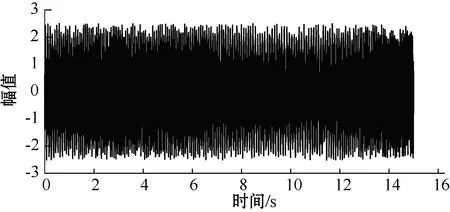
图1 模拟信号s(t)的时域波形

未加入噪声的信号频率变化曲线如图2所示，其瞬时频率

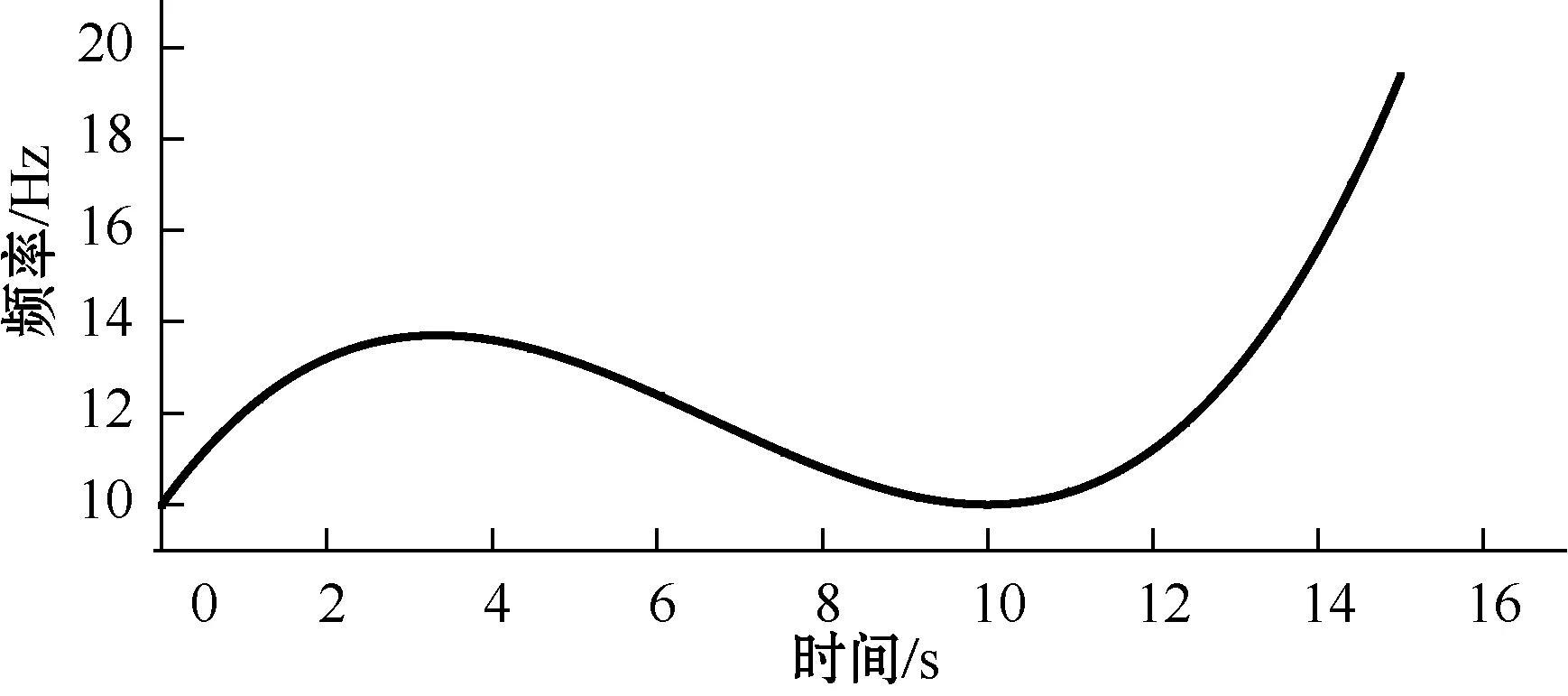
图2 瞬时频率变化曲线

IF=10t+5t/2-t2/2+t3/40t∈[0,15]

使用PCT对加入噪声的s(t)进行分析，得到其时频表示如图3所示。

图3 多项式调频小波变换时频图

从图中可以看到信号在整个时段内都具有很好的能量集中度。

图4是经PCT解算加入噪声后s(t)的频率变化曲线，图5是PCT解算瞬时频率误差。

图4 瞬时频率变化曲线

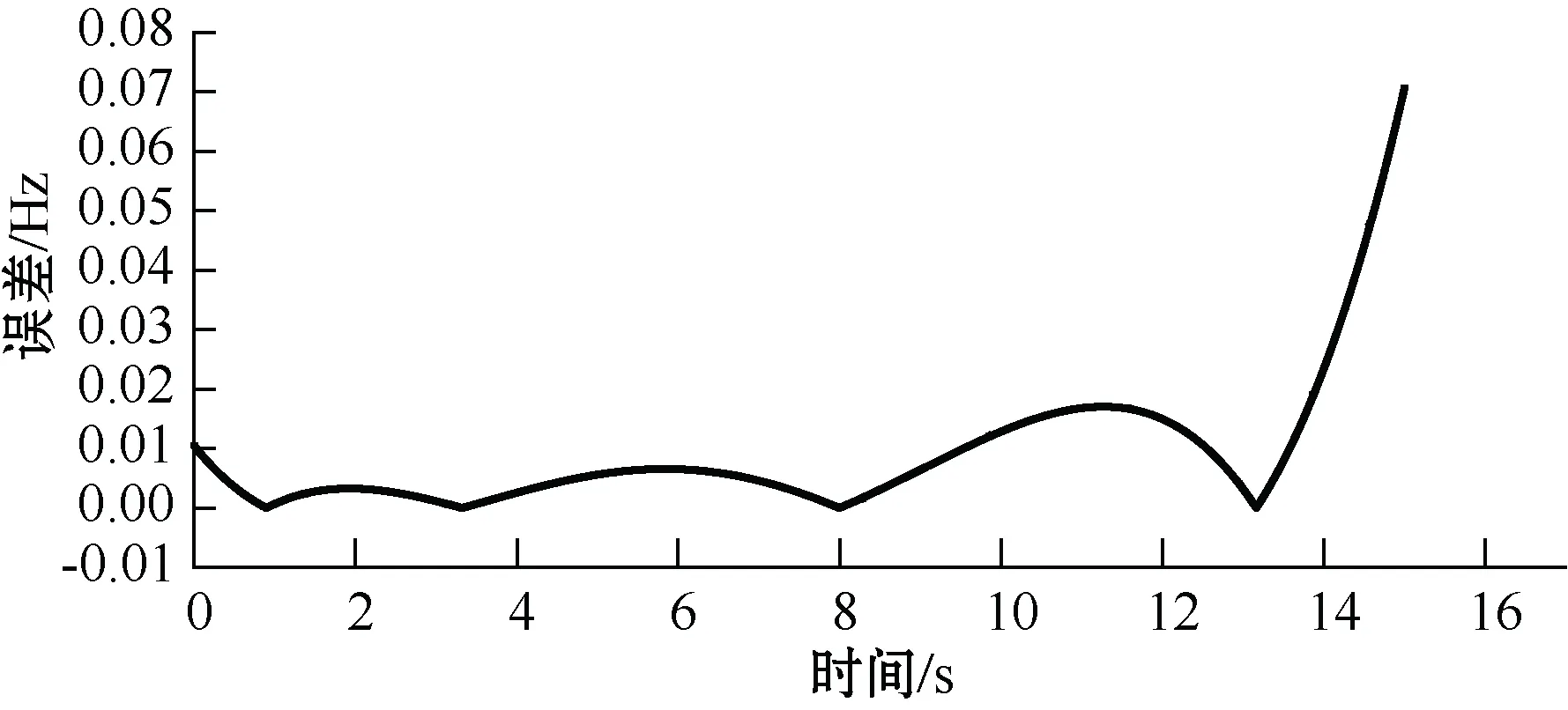
图5 PCT解算瞬时频率误差

从图中可以看到采用PCT对信号的瞬时频率进行求解，误差最大为0.08 Hz，说明该方法时频集中度高、降噪性好，在理论上PCT可以解算多分量信号的瞬时频率。

2 实验验证

飞行体的地磁信号是一个近似正弦的多分量信号，该信号包含地磁信号、环境噪声信号等多种信号，地磁传感器的采样频率为1 000 Hz，截取飞行阶段的数据为实验数据，图6、图7分别为Y、Z轴地磁信号的时域波形。

图6 Y轴地磁信号的时域波形

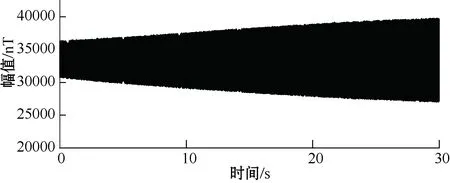
图7 Z轴地磁信号的时域波形

利用PCT对地磁信号进行分析，得到地磁信号的Y、Z时频曲线分别如图8、图9所示。由于PCT计算量大，因此将地磁数据分开计算，图8(a)、9(a)表示前2万个点的地磁信号时频曲线，图8(b)、9(b)表示后2万个点的时频曲线。

图8 Y轴时频曲线

图9 Z轴时频曲线

图10、图11分别表示采用PCT对Y、Z轴地磁信号处理，提取的高动态飞行体转速曲线。由于PCT的条件是分析有限时间段的信号，因此对飞行阶段数据进行截取，图中转速曲线为拼接后的曲线。利用PCT提取地磁信号的转速，PCT作为时频分析方法在分析地磁信号时，具有一定优越性，即当参数选择恰当时，其时频表示集中度较高，能反映信号真实的时频特征，最终实现瞬时转速的准确估计。

图10 Y轴转速变化曲线

图11 Z轴转速变化曲线

3 结束语

高动态飞行体地磁信号是非平稳信号，与传统的非平稳信号分析方法不同的是，PCT通过构造多项式核函数改善了信号时频表示的集中度。

仿真实验结果表明，PCT解算的频率与未添加噪声的信号最大误差仅为0.08 Hz，解算频率精度高，抗噪效果好，在全部的时间频段能量集中度高。

采用PCT处理实测的地磁数据，得到其能量高度集中的时频特性曲线，可以观察到在全部的时间频段内信号的能量集中度都很好，最后从地磁信号中提取转速信号，实验证明PCT可以应用于处理工程信号。