动态滑模在航天器姿态控制中的应用
罗宗樾,管 萍,戈新生
(北京信息科技大学 自动化学院,北京 100192)
0 引言
现代航天器通常配备有大型挠性附件(天线、柔性机械臂、太阳能电池板等),挠性附件与刚体之间的强耦合会在挠性航天器快速跟踪和旋转等姿态控制过程中,引起严重的振动,影响航天器的姿态稳定和指向精度。航天器在实际运行过程中,其姿态控制系统往往会受到空间中各种未知的外部扰动力矩的干扰,因此大挠性航天器的高精度姿态控制一直是通信、导航、遥感等航天任务中的难点和重点[1]。
针对挠性航天器姿态控制的问题,国内外学者进行了相关研究,如PID控制、H∞控制、滑模控制等。文献[2]设计了自适应PID控制器应用于静止卫星姿态控制,该控制器采用了单输入模糊推理机和优先模糊推理机两种模糊推理引擎,保证了系统的稳定和较好的控制性能。文献[3]针对挠性航天器的多目标姿态跟踪问题,提出了一种集成的鲁棒H∞控制器,用H∞方法和凸优化方法解决系统对扰动、参数不确定性和不精确配置的鲁棒性问题。滑模控制对系统不确定性以及外界干扰具有较强的鲁棒性,受到越来越多的关注。文献[4]设计了滑模控制器应用于航天器姿态控制,并在滑模控制律中设计引入滞后因子,以减小系统所需的最大控制力矩,从而节省航天器的控制成本。文献[5]提出了滑模变结构控制器,应用于欠驱动刚体航天器的姿态控制。然而传统滑模为了满足滑动条件,构造了开关控制律,当状态轨迹到达滑模面,由于符号函数的抖振问题,状态轨迹难以沿着滑模面向着平衡点滑动,而是在滑模面两侧来回穿越,而对于传统滑模的高频切换,目前许多实际控制器、执行机构无法实现,因此抖振问题很大程度上限制了滑模控制系统在工程实践上的应用[6]。
国内外许多学者为减少滑模控制系统抖振进行了大量的研究,并提出了多种解决方案。文献[7]用饱和函数代替符号函数,实现导弹的精确打击,但会削弱滑模控制的鲁棒性。文献[8]设计了高阶滑模控制器,应用于空间飞行器的姿态控制,将传统滑模控制律中的不连续项转移到滑模切换函数的高阶导数上,但受到系统相对阶的限制。文献[9]提出了一种动态滑模方法,应用于高超声速航空飞行器的姿态控制,首先将模型进行输入/输出线性化,构造辅助的滑模变量,然后为求取滑模控制量,对不连续的控制量输出加以积分作用,抑制传统滑模控制器的抖振。但是目前在挠性航天器姿态控制系统中鲜少采用动态滑模控制方法。
基于以上分析,本文将动态滑模控制器应用于挠性航天器姿态控制中。采用三轴姿态角描述挠性航天器的姿态运动学方程。针对挠性航天器姿态控制系统,设计动态滑模控制器,将传统滑模控制律中的不连续项引入到控制的一阶导数上,得到本质上连续的动态滑模控制律,有效消除了滑模到达阶段的抖振,抑制了外界扰动和挠性附件振动对姿态产生的影响。
1 挠性航天器姿态的数学模型
挠性航天器姿态动力学方程为[10]:
(1)
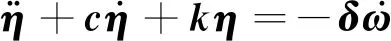
(2)
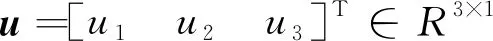
(3)
式中:i=1,2,…,N,N为航天器上挠性体模态的数量;ζi为挠性体振动模态阻尼比;ωni为挠性体振动模态的频率。符号ω×为如下反对称矩阵:
(4)
将式(2)代入式(1)中可得
由上式可得
(5)
用Θ=[φ,θ,ψ]T表示航天器的三轴姿态角,其中φ、θ、ψ分别为滚动角、俯仰角和偏航角。考虑航天器作惯性定向飞行,则在x-y-z转序下的姿态运动学方程可表示为[11]
(6)
(7)
针对挠性航天器系统(7),控制律的设计目标如下:设计控制律u使系统姿态角Θ能够跟踪期望姿态角Θd(Θ→Θd),同时减小挠性附件的振动。
2 动态滑模控制器设计
为使挠性航天器姿态跟踪误差能收敛到零,采用动态滑模算法,对挠性航天器系统式(7),设计动态滑模面如下:

(8)
(9)
式中:a1、a2、b1和b2为非零正常数。
对式(9)求导,并将式(7)和式(8)代入可得

(10)

Jmb=J-δTδ
则式(10)可以写为
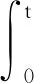
(11)
考虑如下积分切换函数
(12)
其中ξ(t0)为ξ(t)的初始值。
(13)
式中:
(14)
ψdis=-l1ζ-l2sgn(ζ)
(15)
其中:
选取如下Lyapunov函数:
(16)
对式(16)求导,并将式(11)和式(13)代入可得

(17)
选择如下Lyapunov函数:
(18)
结合式(17),对式(18)求导得
(19)
因此,在控制律式(13)作用下,挠性航天器姿态控制系统是稳定的,挠性航天器的跟踪误差可以收敛于零。
3 仿真分析
将所提出的动态滑模控制应用于挠性航天器数学模型上,进行参数仿真研究,挠性航天器所取参数如下[12]:
转动惯量J为
挠性附件与中心刚体间的耦合矩阵为
自然频率为
相应的阻尼为
挠性航天器的初始姿态角和初始角速度设为
挠性航天器姿态期望值设定为
扰动干扰项设置为

控制律参数选取为:a1=0.1,a2=0.01,b1=5,b2=6,k=0.1,β=0.6,α=0.6。
为验证方法的有效性,将本文方法(式(13))与传统滑模控制(文献[13])相比较,仿真结果如图1~4所示。

图1 姿态角Θ的响应曲线

图2 姿态角速度ω的响应曲线
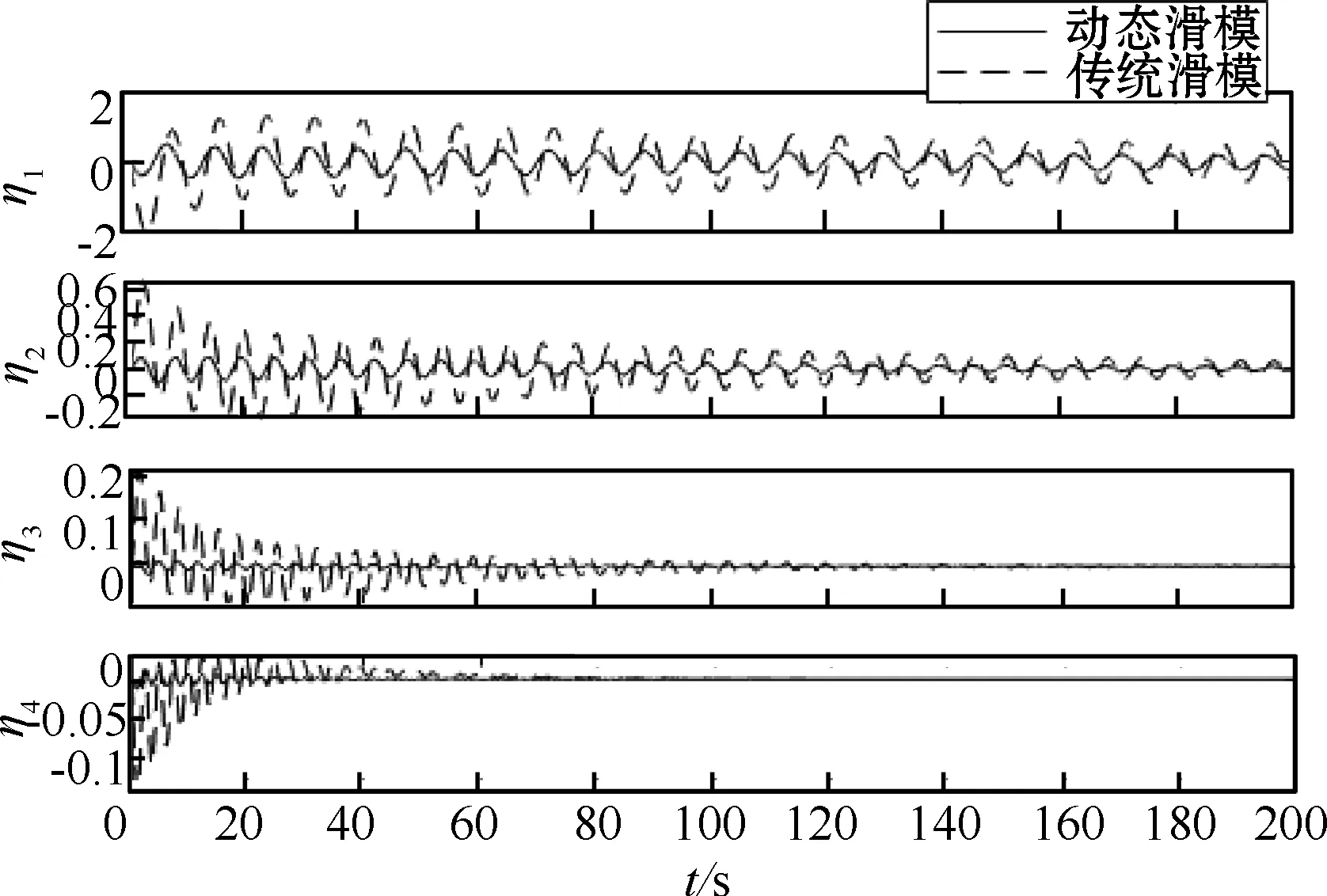
图3 挠性模态位移η的响应曲线

图4 控制力矩u的响应曲线
从图中可以看出,在传统滑模控制下,姿态角和姿态角速度在80 s左右趋于稳定,挠性模态振动幅度较大;在动态滑模控制器下,姿态角和姿态角速度在20 s左右趋于稳定,挠性模态和抑制时间都在30 s以内,且各个阶次挠性模态振动幅度均小于传统滑模控制的振幅。
由以上仿真结果可知,传统滑模控制中姿态稳定时间较长,挠性附件振动幅度较大,振动抑制时间较长,控制力矩有抖振现象;由于动态滑模控制器将传统滑模中的不连续项引入到控制的一阶导数上,由此得到的动态滑模控制律本质上是连续的,控制力矩随时间增加没有抖振现象,姿态响应时间比传统滑模控制的响应时间更短,具有较快的姿态响应速度和较高的稳态精度。
4 结束语
本文针对挠性航天器大角度姿态机动和附件振动抑制问题,采用了动态滑模控制的方法设计姿态机动控制律。将传统滑模控制律中的不连续项引入到控制的一阶导数上,有效地抑制了传统滑模姿态控制律中符号函数项引起的抖振。仿真结果表明,本文方法能有抑制挠性附件振动,对外界扰动有较强的鲁棒性,从而使挠性航天器的跟踪误差能够快速收敛到零,具有较好的控制性能。

