多重Dirichlet级数的线性型及线性准确型

陈覃膻，霍颖莹

（广东工业大学 应用数学学院，广东 广州 510520）

n重Dirichlet级数是具有下列形式的级数：

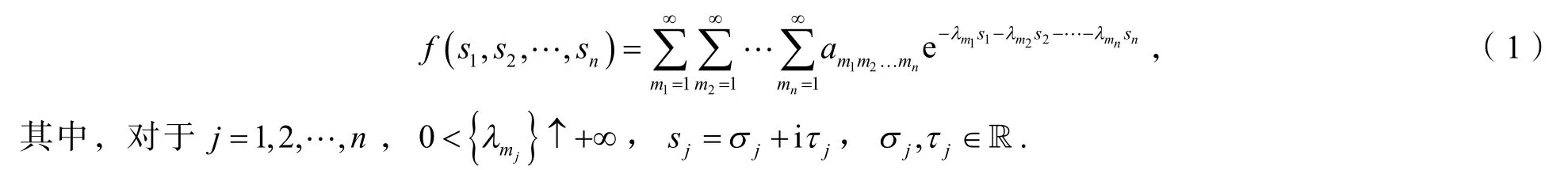
特别地，当1n=时，式（1）为一重Dirichlet级数. Valiron[1]研究了其收敛性并给出了其收敛坐标公式；Ritt[2]定义了一重Dirichlet级数所确定的整函数的级；余家荣等[3]在此基础上研究了一重Dirichlet级数的有限级与其系数、指数间的关系；许全华[4]则在此基础上研究了它的型及其准确型并得到了这些型与其系数、指数间的关系. 关于一重Dirichlet级数的更多理论成果可参考文献[3,5]. 对于式（1），梁美丽等[6]定义了它的线性级并得到了其与系数、指数间的关系，而本文将研究式（1）的线性级所确定的线性型与其系数、指数间的关系.

为了简化级数（1）的表示，记：s=（s1,s2,…,sn）∈Cn，m=（m1,m2,…,mn）∈Nn，λm=（λm1,λm2,…,λmn）∈Rn，并且约定内积λms=（λm1,λm2,…,λmn）（s1,s2,…,sn）=λm1s1+λm2s2+…+λmnsn，则级数（1）就可以简写为：

若记k=（k1,k2,…,kn），那么级数（1）的前m项和为：

一个自然的问题是文献[4]许全华关于一重Dirichlet级数的型的结果是否能推广到多重Dirichlet级数？这里先给出级数（1）的线性型和线性准确型的定义.

定义1当级数（1）的线性级ρ满足0＜ρ＜∞，它的线性型τ定义为

接下来考虑级数（1）的线性准确级. 当0＜ρ＜∞时，文献[8-9]证明存在一个单调递减函数ρ（r）满足

则称ρ（r）为f（s）的线性准确级. 由ρ（r）定义级数（1）的线性准确型.

定义2f（s）关于其线性准确级ρ（r ）的线性准确型τ′定义如下：

本文将许全华关于一重Dirichlet级数的型的结果推广到多重Dirichlet级数，得到了以下结果.

定理2若级数（1）的横坐标分布在Rn中的某一直线Φ，满足条件（2）和（3）且其确定的整函数f（s）具有线性准确级ρ（r） (0＜ρ＜∞)，则其关于ρ的线性准确型τ′满足β≤τ′≤eDφρβ，其中

1 引理

2 定理证明

2.1 定理1的证明

2.2 定理2的证明

令0ε→ 即可证明第2个不等式.

注意到当β有限时τ也有限，结合第一部分证明可知β和τ同时有限或无限，从而定理得证.