加载速率对40Cr 钢Ⅱ型动态断裂特性的影响*
范昌增,许泽建,何晓东,黄风雷
(北京理工大学爆炸科学与技术国家重点实验室,北京 100081)
40Cr 钢是航空航天以及国防领域中使用最广泛的高强钢之一,因其淬透性良好,经热处理后有良好的综合力学性能和低温冲击韧性,常被用于制作机翼大梁、坦克变速器扭轴以及装甲车辆的轴承类零件等[1],但这些构件在服役过程中容易受到冲击剪切载荷的作用而发生Ⅱ型断裂失效。因此,工程材料在Ⅱ型加载下的动态断裂问题日益受到人们的关注,Ⅱ型裂纹在动态载荷下的起裂及扩展行为也成为力学和材料学科的交叉前沿课题。20 世纪80 年代,Kalthoff 等[2-5]发现42CrMo4 钢在低加载速率下Ⅱ型裂纹发生拉伸型失效,裂纹扩展方向与韧带方向成−70°夹角,而在高加载速率下裂纹沿韧带方向以绝热剪切带形式发生失效。Zhou 等[6-8]的研究表明,材料的失效模式转变行为更多地依赖于材料特性,而不是试样的几何形状。Ravi-Chandar 等[9-10]发现,随着冲击速度的增大,聚碳酸酯(PC)的失效模式存在从延性到脆性再到延性的转变,且第二次模式转变会导致裂纹尖端附近形成剪切带。Mason 等[11]对C-300 钢单缺口试件进行动态剪切试验,研究了不同失效形式之间的转换。Chu 等[12]对金属材料的韧脆模式转变进行了相场损伤演化,发现应力波的传播在脆性-韧性破坏模式转变中起着重要作用。在实验测试方面,莫尔云纹法、全息法和光弹性法等光测力学方法[13-15]已被应用到断裂试验中[16-20],并取得了满意的效果。但是,目前对于高强钢Ⅱ型裂纹在冲击载荷下失效行为的研究大多仍采用类似Kalthoff 的加载方法或单杆加载方法对单边裂纹试样进行测试[21],这类加载方法不易于对断口形貌特征的转变行为进行定量控制和精确测量。近期,许泽建等[22-24]提出了一种新型Ⅱ型动态断裂实验方法,该方法可以实现对加载速率的精确控制,从而可以对材料的失效模式转变行为进行系统的量化研究。他们通过对TC4 材料的研究,发现失效模式转变(FMT)不是突变的结果,而是受不同微观机制主导的渐变过程。随着加载速率的增加,材料的失效模式及断口特征均发生改变,是多种失效机制协同作用的结果。以上结果为Ⅱ断裂的失效行为研究提供了新的方法和思路。
本文中采用该新型Ⅱ型动态断裂实验方法,基于分离式霍普金森压杆(SHPB)技术[25],对40Cr 高强钢开展不同加载速率下的动态断裂实验;采用实验-数值方法确定材料的动态断裂韧性值,并通过高速摄影观察裂纹的起裂及扩展过程;结合试样断口的宏、微观形貌特征分析,对材料的失效模式及微观机理进行研究。
1 实验方法
采用SHPB 系统[26]对Ⅱ型裂纹进行动态加载和测量,并采用实验-数值方法对裂尖的应力强度因子和断裂韧性进行确定。实验时,通过入射杆对特殊设计的Ⅱ型断裂试样进行加载,并在裂尖形成Ⅱ型载荷,试样的几何外形及尺寸如图1 所示。入射杆、透射杆和试样上均贴有应变片,分别记录入射波 εi(t) 、透射波 εt(t) 信号和试样的起裂信号。为避开裂尖的塑性区,试样上应变片的粘贴位置位于裂尖的一侧,应变片中心点位于距离裂尖约3 mm 处(见图1)。根据一维应力波理论,可获得压杆与试样接触面处的载荷和位移曲线,如下式:

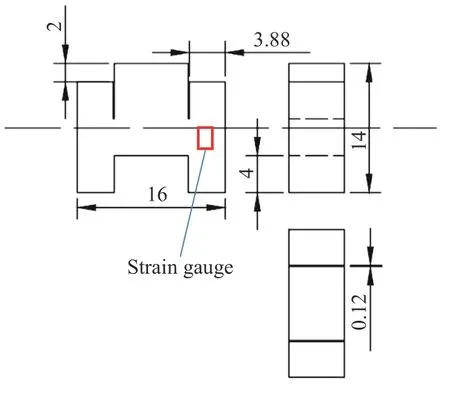
图1 Ⅱ型断裂试样几何尺寸(单位:mm)Fig. 1 Geometric dimensions of the mode Ⅱfracture specimen (unit: mm)
把实验所测入射杆的应力波波形与实际位移边界条件等作为输入量,对试样的受载过程进行数值模拟,并通过位移法[22]计算裂尖的应力强度因子曲线KⅡ(t),如下式:

式中:Fin、Fout为入射杆与透射杆端部的载荷,Uin、Uout为入射杆与透射杆端部的位移,A为横截面积,E为杨氏模量,c0为杆的纵波波速,r为距裂尖的距离,G为剪切模量,µ为泊松比,u(r,t)为裂尖位移场。
在此基础上,结合试样的起裂信号可以确定材料的Ⅱ型动态断裂韧性。
另外,裂尖的加载速率K˙Ⅱd可由下式确定:

式中:tf为试样的起裂时间,KⅡd为动态断裂韧性。
实验材料为40Cr 高强钢,元素成分见表1,热处理工艺为:40Cr 正火850 ℃,冷却方式为空冷,40Cr 淬火温度为780 ℃,冷却方式为水冷,回火温度为200 ℃,冷却方式为空冷。针对同批次、同炉热处理的材料进行了力学性能测试,得到40Cr 材料的力学性能测试参数,见表2,表中ρ 为密度,E为弹性模量,µ为泊松比,σb为抗拉强度。实验中通过控制气压大小和子弹长度来控制加载速率。
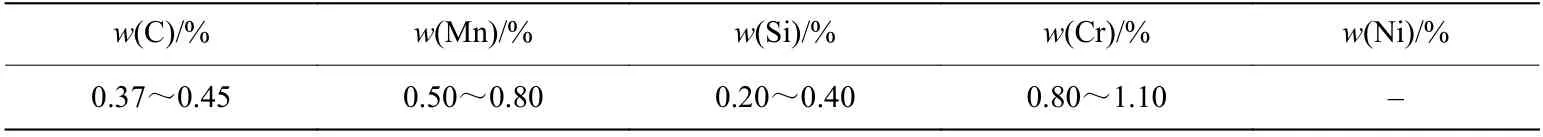
表1 高强钢40Cr 的元素成分及质量分数Table 1 Composition and mass fraction of high-strength steel 40Cr

表2 高强钢40Cr 的力学性能参数Table 2 Mechanical properties of high strength steel 40Cr
在1.08~5.53 TPa·m1/2/s 加载速率范围内对40Cr 试样进行动态加载,为避免压杆中反射的应力波对试样造成重复加载,实验中采用了单脉冲加载技术[27]。图2 为在4.86 TPa·m1/2/s 加载速率下获得的原始波形。由图2 可知,反射波在入射杆端部经单脉冲系统吸收后,剩余的反射波成分很少,幅值接近于零,因此可以实现对试样的单次加载。通过该技术,可以避免压杆中因应力波的反射给试样造成重复加载,有利于对材料的失效模式进行确定和研究。另外,试样的起裂时间采用应变片法[22]进行测定,原理为当应力波作用于试样时,试样先发生弹性变形,此时应变信号从零开始线性增加;当裂尖出现塑性区并开始起裂时,模拟中试样应变信号与实测信号发生分离,其分离点即为起裂时间。这部分时间包括了裂尖起裂时的应力波传到应变片的时间[23],见下式:
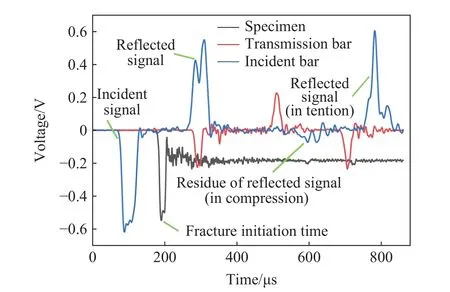
图2 典型实验信号(4.86 TPa·m1/2/s)Fig. 2 Typical experimental signals (4.86 TPa·m1/2/s)

式中:D为应变片中心到裂尖的距离,B为试样的厚度,c0为卸载波的波速, 一般为弹性波纵波波速。
2 实验结果
在1.25 TPa·m1/2/s 加载速率下的实验波形如图3 所示,试样发生了拉伸型起裂。由图3 可知,反射波电压先上升到0.2 V,然后骤降;与此同时,透射波信号也不断降低。在138 µs 左右,反射波恢复到0.2 V并保持稳定,透射波对应的信号上升至−0.1 V。结合高速摄影观察分析知,反射波与透射波信号下降阶段对应于应力波对试样的加载过程,此过程中试样始终与压杆保持接触,且试样发生起裂但尚未完全断裂。当反射波信号上升至0.2 V、透射波信号上升至−0.1 V 时,试样完全起裂,且通过高速摄影观察可知,试样单边支撑端先发生断裂。此后透射端载荷未降至0 V,说明该阶段透射杆与试样支撑端仍保持接触状态。

图3 试样拉伸起裂的典型信号(1.25 TPa·m1/2/s)Fig. 3 Typical signals of tensile fracture initiation of a specimen (1.25 TPa·m1/2/s)
在4.86 TPa·m1/2/s 加载速率下的实验波形见图4,试样发生绝热剪切型断裂。由图4 可知,反射波电压在上升到0.45 V 后开始缓慢下降;与此同时,透射波信号也较为平缓地下降。在38 µs 左右,反射波恢复到0.5 V 并保持稳定,透射波对应的信号上升到0 V。结合高速摄影(见图5)观察分析知,反射波与透射波信号下降阶段对应于应力波对试样的加载过程,此过程中试样始终与压杆保持接触,且试样发生起裂但尚未完全断裂。当反射波电压值保持为0.5 V、透射波电压保持为0 V 时,试样完全起裂,且通过高速摄影观察可知试样双边支撑端同时发生断裂。此后透射波电压降为0 V,说明该阶段透射杆与试样两支撑端已脱离接触。
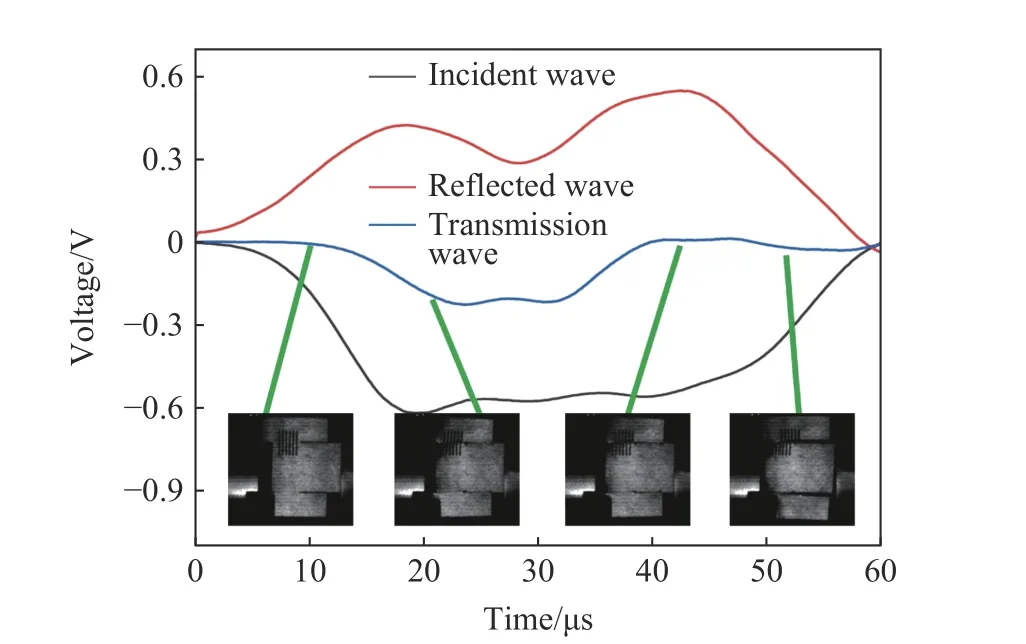
图4 试样绝热剪切起裂的典型信号(4.86 TPa·m1/2/s)Fig. 4 Typical signals of ASB initiation of a specimen (4.86 TPa·m1/2/s)
以上两次实验的加载过程如图5 所示,其中图5(a)、(e)分别为试样初始受载时刻;图5(b)、(f)为试样裂尖开始起裂的时刻,可以观察到此时裂尖局部出现白亮区域,说明已经发生了小范围屈服现象;图5(c)、(g)为不同加载速率下试样完全断裂的失效形态。根据以上分析可将加载过程分为2 个阶段:第1 阶段为从试样开始受载到临界起裂(即出现白点)的阶段,此阶段表现为试样吸收能量发生弹性变形,同时在裂尖区域形成小范围塑性变形和微裂纹;第2 阶段是从裂尖处的微裂纹集聚形成新的界面(即发生起裂)至试样以拉伸型或绝热剪切型失效模式发生完全断裂。在第2 阶段,随着加载速率的增加,裂纹扩展角及扩展路径也随之发生变化。该现象说明裂纹扩展过程中裂尖的应力状态和材料特性会发生改变并决定着裂纹面的发展趋势。

图5 拉伸型起裂(1.25 TPa·m1/2/s)与ASB 型起裂(4.86 TPa·m1/2/s)的高速摄影图Fig. 5 High-speed photographic images of tensile fracture initiation (1.25 TPa·m1/2/s) and ASB initiation (4.86 TPa·m1/2/s)
3 分析及讨论
3.1 有限元模拟及验证
有限元模拟采用ABAQUS/Explicit,此软件的显示动力学模块在计算高速冲击加载和接触性问题时具有显著的优势。根据实际工况和尺寸进行1∶1建模,并将实测的入射杆应力波作为输入量。入射杆、透射杆和试样的材料均定义为线弹性模型,参数见表3;入射杆、透射杆与试样的接触端面均设为法向硬接触,并在试样支撑端的侧面施加横向位移约束以模拟实际工况中夹具的限位作用。入射杆与透射杆均采用八节点六面体单元;为提高计算精度,在裂尖区域采用六面体-楔形体-四面体的过渡方式划分网格,并进行网格细化,使裂纹端部与裂纹半长处的网格尺寸比值控制在0.001~0.02 之间,此时裂尖弹性应变场的计算误差约为1%。模型装配图如图6 所示。

图6 试样裂尖网格细化Fig. 6 Mesh refinement of the specimen crack tips

表3 入射杆、透射杆的力学性能参数Table 3 Mechanical properties of the incident and transmission bars
将模拟结果中试样粘贴应变片区域的应变信号与实测的应变信号进行对比,如图7 所示。当材料处于线弹性阶段时,试样的模拟真实应变与实测的试样应变信号基本吻合,佐证了材料参数的准确性以及有限元模拟的可靠性。当时材料处于塑性变形阶段,且实测应变为0.005 时,模拟信号与实测信号发生分离,该分离点作为起裂时刻。由图8 可知,随着子弹速度的增加,试样的起裂时间明显提前,且基本保持线性关系。采用位移法确定的应力强度因子(dynamic stress intensity factor, DSIF)曲线如图9 所示。根据起裂时间,在DSIF 曲线上确定了试样Ⅱ型断裂韧性,结果见表4。图10 中还给出了文献[21]采用单杆加载单边裂纹试样方法所测出的40Cr 钢动态断裂韧性结果。从图10 中可看出,新型Ⅱ型加载方式测得的动态断裂韧性DFT(dynamic fracture toughness)明显高于文献结果,这可能是由于文献中的单杆加载方式在对试样加载的过程中,单边裂纹在弯矩作用下出现了Ⅰ型断裂现象(即张开型断裂),因此裂尖起裂时受到Ⅰ型断裂的影响,导致所测得的Ⅱ型动态断裂韧性值偏低。

图7 试样的实测应变与模拟应变Fig. 7 The measured strain and simulated strain of the specimen

图8 子弹速度与起裂时间的关系Fig. 8 Relationship between bullet velocity and crack initiation time

图9 不同加载速率下的DSIF 曲线Fig. 9 DSIF curves at different loading rates
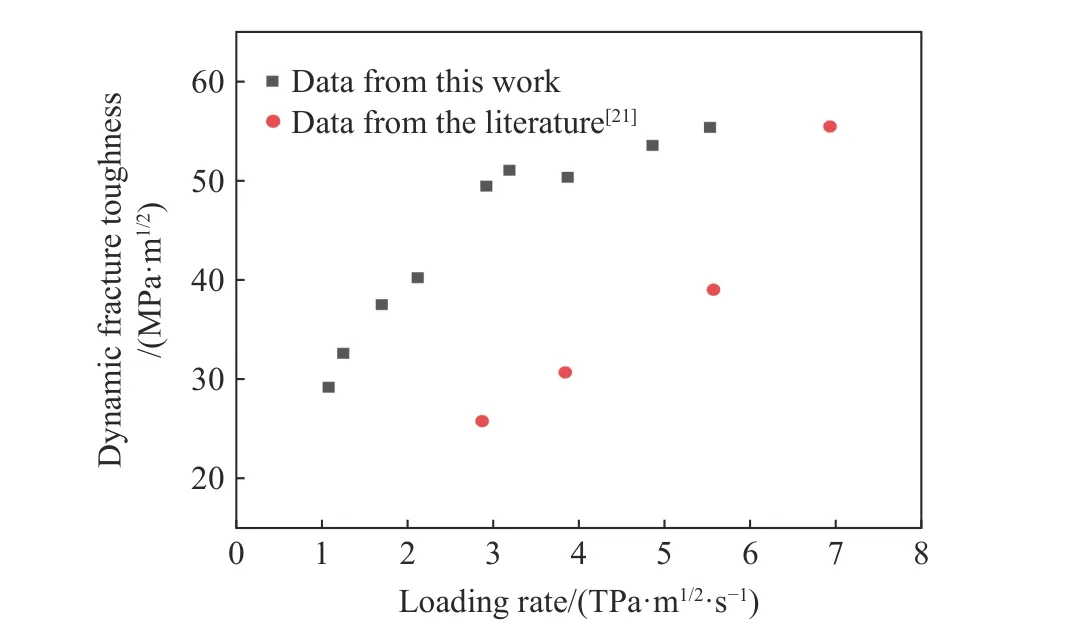
图10 不同加载方式下的DFT 与加载速率关系图Fig. 10 Relationship between DFT and loading rate under different loading methods

表4 高强钢40Cr 的动态断裂韧性值Table 4 Dynamic fracture toughness values of high strength steel 40Cr
综上所述,当加载速率在1.08~5.53 TMPa·m1/2/s范围时,40Cr 材料Ⅱ型断裂韧性与加载速率呈现正相关趋势。其中当≤2.92 TPa·m1/2/s时,40Cr 试样均属于拉伸型失效模式,裂纹扩展方向与韧带方向夹角由−60°逐渐减小至−45°,动态断裂韧性(DFT)与加载速率的拟合表达式为y=10.45x+18.83;当≥3.19 TPa·m1/2/s时,试样均表现为绝热剪切型失效模式,裂纹扩展与韧带方向夹角约为−16°,拟合表达式为y=2.09x+43.39。
3.2 断口形貌分析
采用Phenom Pro扫描电镜对试样断口形貌进行观察,根据形貌特征分为脆性、韧性以及绝热剪切型3种断口。由图11可知,拉伸型失效模式下存在脆性、韧性两种断口形貌,而绝热剪切型失效模式下仅存在绝热剪切型断口形貌特征。在不同的断口形貌下,DFT与的线性拟合参数见表5。
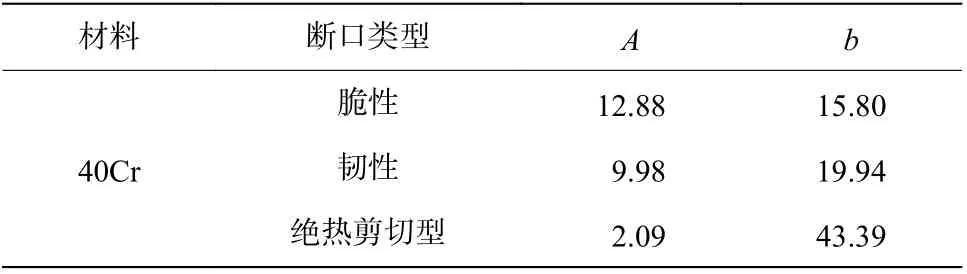
表5 不同断口形貌下DFT与加载速率的线性拟合参数Table 5 Linear fitting parameters of DFT and the loading rates under different fracture morphology
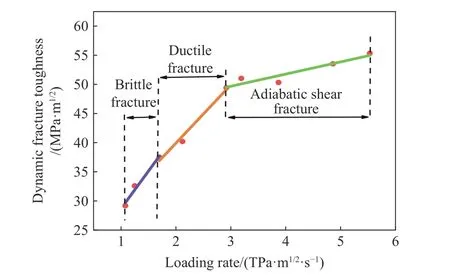
图11 不同断口形貌特征的DFT 与加载速率关系图Fig.11 Relationship between DFT and loading rate of different fracture morphology characteristics
在中加载速率(2.12 TPa·m1/2/s≤≤2.92 TPa·m1/2/s)下,40Cr 试样断口宏观上呈亮灰色,断面有平滑的剪切滑移带且有金属光泽。将图13局部区域放大后可观察到明显的韧性断口形貌特征:抛物线型的剪切韧窝以及平滑的长条状形貌。其原因一般为微孔洞在剪切应力作用下萌生、成核、长大、集聚形成剪切韧窝,随着加载速率的增加,形变不断加剧,由此产生的绝热温升使剪切韧窝软化,同时在剪切应力作用下被快速剪切为平滑的长条状形貌,甚至形成无特征的平坦面,该区域面积占比伴随着加载速率的增大而不断增大。因此,在中加载速率下,40Cr 材料断口属于由应变/应变率硬化以及热软化机制共同主导的韧性断裂模式。

图13 40Cr 试样韧性断裂特征(2.92 TPa·m1/2/s)Fig.13 Ductile fracture characteristics of 40Cr specimen (2.92 TPa·m1/2/s)

图14 40Cr 试样绝热剪切型断裂特征(3.87 TPa·m1/2/s)Fig.14 Adiabatic shear fracture characteristics of 40Cr specimen (3.87 TPa·m1/2/s)
由以上分析可知,不同加载速率下,材料的断口形貌特征也不同。低加载速率下,40Cr 材料断口属于由应变率硬化机制主导的脆性断裂模式;中加载速率下,属于由应变/应变率硬化以及热软化机制共同主导的韧性断裂模式;高加载速率下,属于由热软化机制主导的绝热剪切型断裂模式。
4 结 论
采用新型Ⅱ型动态断裂测试技术,对40Cr 钢进行了不同加载速率下的Ⅱ型动态断裂特性研究,得到如下结论:
(1)在加载速率范围(1.08~5.53 TPa·m1/2/s)内,40Cr 材料的Ⅱ型断裂韧性值与加载速率基本呈正相关趋势。
(2)在1.08~5.53 TPa·m1/2/s的加载速率范围内,40Cr 存在拉伸型失效模式向绝热剪切型失效模式转变,且临界加载速率为2.92 TPa·m1/2/s。
(3)当K˙Ⅱd≤1.70 TPa·m1/2/s时,40Cr 材料的断口表现为脆性断裂;当K˙Ⅱd介于2.12~2.92 TPa·m1/2/s之间时,断口表现为韧性断裂;当K˙Ⅱd≥3.19 TPa·m1/2/s时,断口表现为绝热剪切型形貌特征。
(4)脆性断裂由应变率硬化机制主导,韧性断裂由应变/应变率硬化和热软化机制共同主导,绝热剪切型断裂由热软化机制主导。

