冲击载荷作用下圆孔缺陷对裂纹动态扩展行为的影响规律*
王 磊,朱哲明,周 磊,2,董玉清,牛草原,杨正艳
(1.四川大学建筑与环境学院深地科学与工程教育部重点实验室,四川 成都610065;2.成都理工大学地质灾害防治与地质环境保护国家重点实验室,四川 成都610059)
深部地下岩体结构中,岩体周围不仅会存在裂纹、节理与断层等各种缺陷,而且岩体周围也可能存在圆形或椭圆形等不同形状的空腔。当地下岩体结构受到突如其来的地震或爆破等动力扰动载荷作用时,岩体结构中的裂隙与空腔的共同作用将会导致岩体结构整体的失稳坍塌,最终造成岩体结构垮塌、泥石流、地裂缝、地面沉降等各种地质灾害,同时伴随着惨烈的人员伤亡和大量的经济损失[1-3]。因此,很有必要对含空腔缺陷裂隙结构的动态破碎行为进行分析研究。
在静态断裂力学方面,Fan 等[4]采用单轴压缩实验测试了含有单孔双裂纹缺陷和双孔双裂纹缺陷的矩形砂岩试样的破坏形态。Gong 等[5]给出了Ⅰ/Ⅱ型裂纹缺陷尖端附近存在椭圆孔缺陷时的理论求解的方法,并用复变函数的方法得到了Ⅲ型应力强度因子的表达式。Meguid 等[6]用积分变换和贝塞尔函数计算了在反平面载荷下裂纹尖端附近任意位置存在圆孔缺陷时的理论解。在动态断裂力学方面,杨仁树等[7]用动态焦散线实验方法,研究了圆孔缺陷对原生裂纹在爆炸载荷下扩展行为的影响,结果表明,爆生裂纹扩展到圆孔附近时裂纹扩展速度会增加;李盟等[8]研究了双孔对爆生裂纹动态扩展行为的影响,结果表明双孔会降低裂纹的扩展速度。
地质灾害的常见诱因包括地震、爆破、工程开挖等,它们都属于动力扰动载荷。因此本文将基于动态载荷研究岩体内裂纹的动态扩展规律,包括裂纹的扩展速度,扩展机理及扩展韧度等。近年来,研究岩石动态断裂行为的方法主要有实验-数值模拟法[9-10]、高速摄影法[11-12]、应变片法[13-14]、动态焦散线法[15,16]、动态数字图像相关法[17]等。研究内容主要聚焦于裂纹扩展的动态起裂、动态扩展及动态止裂三阶段[18-23],但很少有研究综合考虑了空腔缺陷与裂纹缺陷共同遭受动力载荷作用下的破碎行为演变规律。
此外,分离式霍普金森压杆(split Hopkinson pressure bar,SHPB)装置已经被广泛运用于动力学实验的相关研究[24-25],但是由于其杆件的直径较小,不适于大尺寸试件的冲击实验。因此,基于SHPB原理,团队设计了适用于大尺寸试件动态断裂行为研究的大型落锤冲击实验装置。并且本文创新性提出了直裂纹空腔圆弧开口试件(circular opening specimen with straight crack cavity,COSSCC),然后利用落锤冲击实验装置进行动态加载,同时搭配裂纹扩展计(CPG)监测裂纹扩展的动态断裂过程,随后借助于数值计算软件进行了裂纹破坏行为的时效变形数值分析,完善与补充动态实验数据捕捉的局限性,模拟出裂纹扩展过程中的应力场变化情况以及计算动态断裂韧度值,最后结合实验结果和数值模拟结果分析裂纹的扩展形态及其扩展机理。
1 实 验
1.1 实验模型
实验采用脆性材料有机玻璃(polymethyl methacrylate,PMMA),相对于岩石,它具有更好的均质性和透光性,方便于测试与观察裂纹的起裂与扩展行为。PMMA 材料的密度为1180 kg/m3,弹性模量为6.1GPa,泊松比为0.31,纵波波速cp为2320 m/s,横波波速cs为1260 m/s。试样的制备是由工厂定制,裂纹缺陷和圆孔缺陷都是采用激光线切割的方法,用这种工艺切割的裂纹,加工精度高,切口光滑平整,其切割缝隙宽度为0.1 mm,能够有效减小裂纹宽度对实验结果造成的影响。
直裂纹空腔圆弧开口试件尺寸如图1所示,首先在300 mm×400 mm×30 mm 的矩形有机玻璃板试样上端切割直径为150 mm 的半圆弧,圆弧开口能够使得裂纹更容易起裂与扩展,裂纹起裂阶段能够更好的表征为纯I型裂纹断裂特征,防止起裂阶段裂纹尖端剪应力场对裂纹扩展行为的影响,能够更好地分析圆孔缺陷对裂纹扩展路径的影响规律,这是在研究团队前期研究基础上所证明的优势构型[26]。随后激光切割圆孔缺陷的直径为10 mm,切割预制裂纹长度为50 mm,并使得裂纹尖端与圆孔圆心直线距离为50 mm,而裂纹尖端与圆孔中心连线的夹角定义为θ,即圆孔的倾角。为了探究不同倾角的圆孔对裂纹扩展的影响规律,本次实验以圆孔倾角θ 为变量设计了θ 分别为0°、10°、20°、30°、40°和50°的6组实验,每组实验制备3 个试件。试件命名#00-1表示圆孔倾角为0°的1号试件,#30-3为圆孔倾角为30°的3号试件。
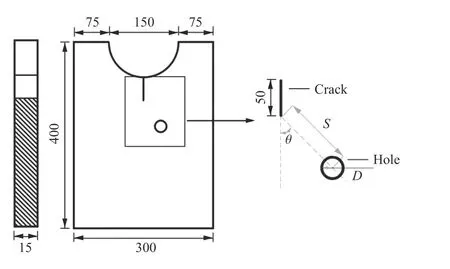
图1 试件的构型及尺寸(单位:mm)Fig.1 Sketch map of specimen (unit:mm)
1.2 动态加载实验设备
采用基于SHPB原理设计的落锤冲击实验装置,如图2所示,该装置主要由落锤、入射板、透射板、阻尼器组成。冲击锤是尺寸为480 mm×150 mm×30 mm 的钢板,动态实验时让其自由落体撞击入射板,使入射板能够获得一个正弦应力脉冲信号。入射板和透射板均采用LY12CZ铝合金材料制作,经过测试得到其弹性模量为71.7 GPa,密度为2850 kg/m3,纵波波速为5006.5 m/s,泊松比为0.33。其中入射板的尺寸为300 mm×3 000 mm×30 mm,透射板的尺寸为300 mm×1000 mm×30 mm。经过前期多次测试,在入射板距离底端75 mm 处贴一个应变片(strain gauge,SG)测量入射波和反射波信号,在透射板距离顶端75 mm 处贴应变片测量透射波信号。在入射板顶端配置一块黄铜片,其作用是减小加载波形的高频振荡和弥散效应,同时也可以提高加载波的上升沿[27]。加载前,在COSSCC试件上下端涂抹黄油,以减小试件与入射杆底端和透射杆顶端之间的摩擦力。
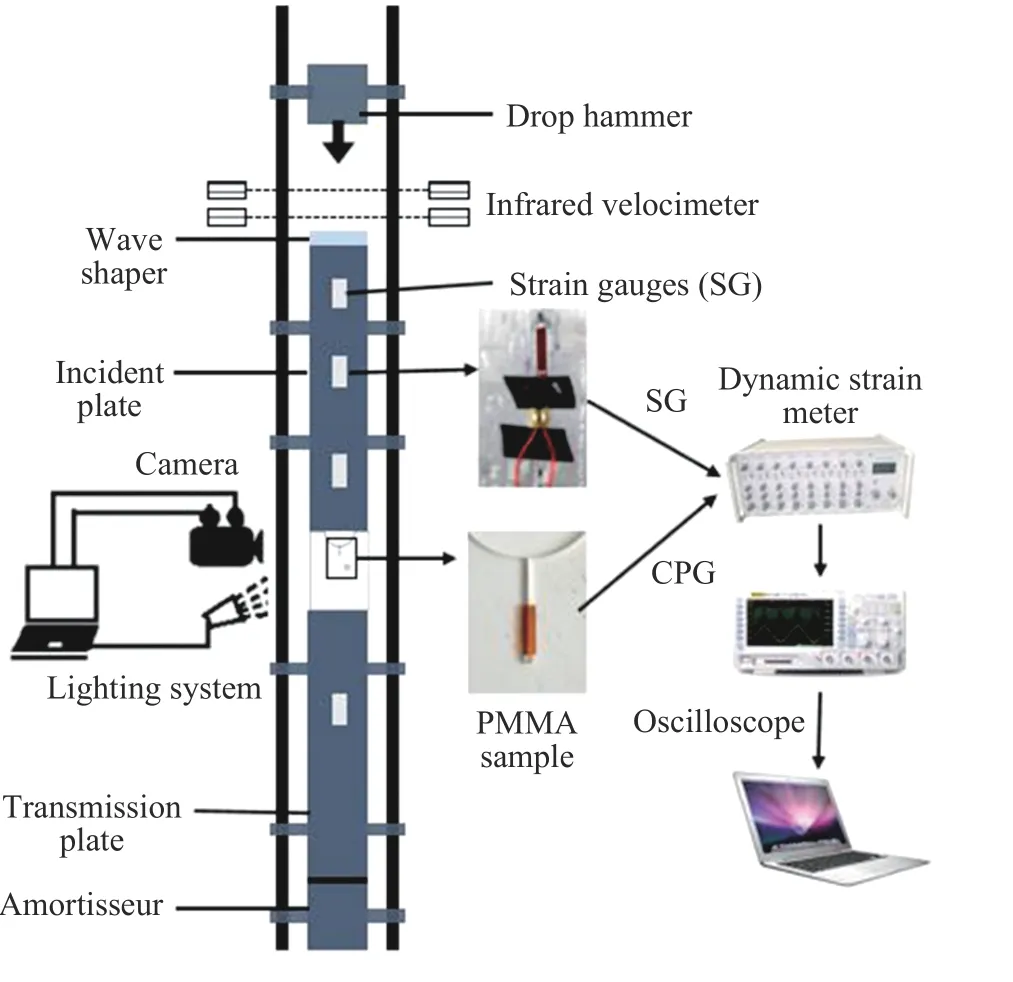
图2 落锤冲击实验装置Fig.2 Drop hammer impact test system
1.3 裂纹扩展计测试系统
实验采用裂纹扩展计(crack propagation gauge,CPG)采集实验数据,CPG型号为BKX3-17.8CY-21-W,电阻值为3.5Ω。CPG 如图3所示。裂纹扩展计由基底、引线、两根横向栅丝和21根竖向栅丝构成。21根竖向栅丝相当于21根阻值不同的电阻,分别命名为R1,R2,···,R21,它们被两根横向栅丝并联起来。CPG 监测裂纹扩展的有效长度即为横向栅丝接入电路的有效长度,值为L=44 mm,竖向栅丝的长度为b=20 mm。在本实验中,先将CPG 与一个50Ω 的电阻并联,然后再串联一个阻值为50 Ω的电阻,这样可以保证CPG两端电压变化不会太大从而影响实验结果的精度。整个电路由一个16 V 的稳压源提供稳定的电源电压。CPG可以监测到裂纹扩展到CPG 每根栅丝位置的时刻,其原理是:实验时,将CPG粘在试件待测位置,CPG的栅丝会随着裂纹的扩展一起断裂。当CPG上的敏感栅丝每断一根,CPG 的总电阻值就会产生突变。将CPG 接入电路中,电阻值的突变就会表现为输出电压值的突变,而突变时刻就是CPG 金属栅丝的断裂时刻,也就是裂纹扩展到栅丝位置的时刻,设裂纹扩展到Rn栅丝位置的时刻为tn.,在粘贴CPG 时,保证裂纹尖端与CPG 第1根栅丝R1位置重合,以确保R1的断裂时刻t1即为裂纹的起裂时刻tf。裂纹扩展经过相邻两根栅丝的距离都为l0=2.2 mm,这样就可以算出裂纹扩展经过相邻两根栅丝之间的平均裂纹扩展速度vn:

图3 裂纹扩展计(CPG)示意图Fig.3 Sketch map of the crack propagation gauge (CPG)

裂纹扩展经过CPG 的21栅丝的平均速度为va:

1.4 实验结果分析
实验中,入射板和透射板上的应变片分别独立的接入两个桥式电路中,采用单臂桥式电路,应变片型号为BX120-5AA,张贴在入射端和透射端的应变片分别接入单臂桥式电路中,应变片测得应变ε 和电桥的输出电压∆U应满足:

式中:n为超动态应变仪控制的增益系数,实验时该增益系数设置为n=1000;电桥电压E=2 V;应变片的灵敏度系数KS=2.1。
在动态加载过程前,用红外线测距仪测量落锤冲击高度,随后根据动能定理,可计算得到落锤的下落冲击速度。落锤冲击实验中,各组实验的落锤冲击高度均约为1.8 m,计算得到落锤产生的冲击速度约为6.0 m/s。每组试件冲击完成后,记录入射板和透射板上应变片的电压信号数据。这个电压信号就是入射波、反射波和透射波电压信号。由于实验室存在干扰,实验采集到的信号数据难免有噪点,因此将得到信号导入Origin 软件中做降噪处理和寻找波头[28],处理得到入射波、反射波、和透射波应变如图4(a)所示。
根据一维弹性应力波假设[29],入射波和反射波的叠加可以得到入射板对试件的载荷,而透射波是透射板对试件的载荷,即:

式中:Pi为入射板对试件的载荷;Pt为透射板对试件的载荷;A为入射板、透射板与试件的接触面积;E为入射板与透射板材料的弹性模量;εi为入射波应变;εr为反射波应变;εt为透射波应变。叠加后的入射端和透射端的加载曲线如图4(b)所示,这个加载曲线将导入有限元软件中,作为加载边界条件计算应力强度因子。

图4 入射波和透射波信号Fig.4 Signals of incident wave and transmitted wave
通过实验测得CPG的电压信号,将采集的数据导入数值分析软件Origin 中,再对电压信号求导,导数的极值对应为电压信号的突变时间,即为栅丝的断裂时间,如图5所示。图5(a)为#00-1号试件的CPG 电压信号,可以看到,裂纹扩展经过21根栅丝,相应的CPG 电压信号出现了21个台阶。并且电压信号的第21 个台阶明显较窄,意味着裂纹扩展从栅丝R20到R21的时间较短,即此处的裂纹扩展速度较大。而对于#20-3和#40-2号试件,电压信号的第21个台阶没有出现明显变窄的现象,即此处裂纹的扩展速度没有显著增大,如图5(c)~(e)所示。图5(a)、(c)、(e)中红色曲线即为电压信号的导数,可以看到导数曲线都出现了21 个极值点,极值点对应的时间即为21根栅丝分别断裂的时间,特别地,第1根栅丝R1的断裂时间即为裂纹的起裂时刻tf,试件#00-1的起裂时刻为423.2µs,试件#20-3的起裂时刻为425.6µs,试件#40-2的起裂时刻为424.4µs。图5(b)为#00-1的裂纹动态扩展速度和裂纹扩展位移时程曲线,可以看出裂纹扩展速度基本在200~350 m/s范围内,裂纹扩展的平均速度va为281.79 m/s。比较特别的是,当裂纹扩展到栅丝R21时,裂纹扩展速度出现了显著的增大,达到了464.60 m/s,而此时裂纹距离圆孔边缘仅1 mm。而对于试件#20-3和试件#40-2,裂纹扩展到第21根栅丝时,裂纹尖端距离圆孔边缘分别为12.4 mm 和27.6 mm,此时裂纹扩展速度并没有出现显著增大,如图5(d)和5(f)所示。并且计算出裂纹的平均扩展速度va分别为235.59 m/s和254.79 m/s,均小于试件#00-1的裂纹的平均扩展速度va。
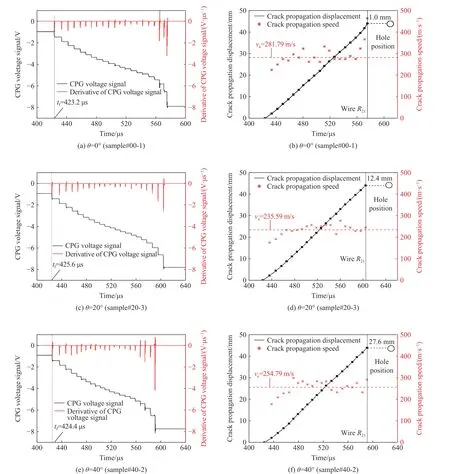
图5 CPG 测试数据Fig.5 Test results of CPG
各组实验的CPG 测试数据如表1所示。从表中可以看出,各组试样的裂纹起裂时刻均在417~427µs之间,其最大差距小于2%,因此,在误差范围内,可以认为圆孔对裂纹的起裂时间没有影响。而其误差可能是由于试样制备时,激光切割的预制裂纹尖端的尖锐程度不同,导致裂纹起裂的难易程度产生细小的差异,使得裂纹的起裂时间存在着误差。
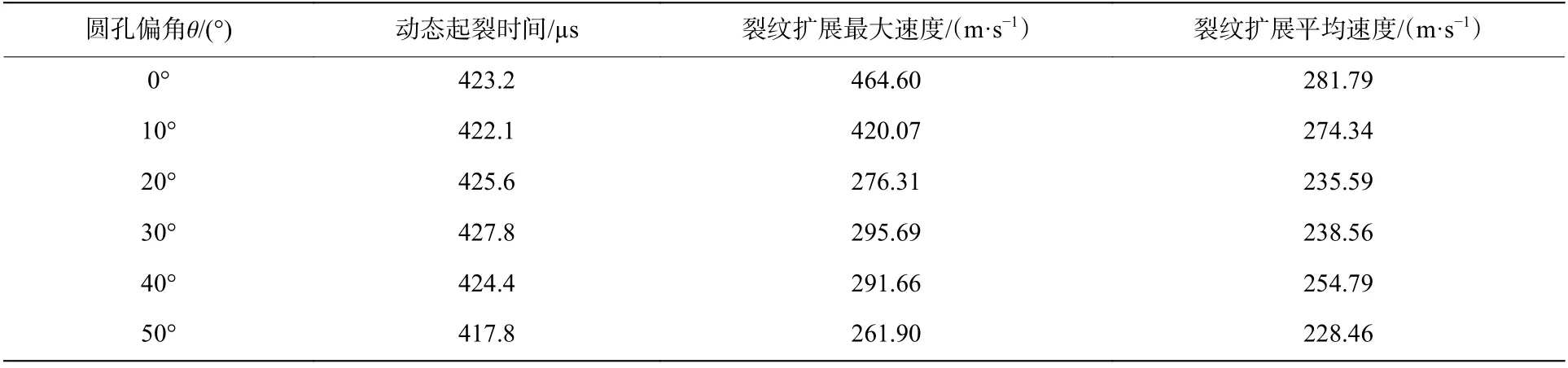
表1 各组式样的CPG 测试结果Table 1 CPG test results of each specimens
各组试件的裂纹扩展变化趋势如图6所示,对于θ=0°的编号为#00-1试样,裂纹扩展从栅丝R1到栅丝R21时,裂纹扩展速度发生小幅度的波动,但当裂纹扩展到达栅丝R21,距离圆孔边缘1 mm 时,裂纹扩展速度显著增大,并且达到最大值464.60 m/s;对于θ=10°的编号为#10-3的试样,同#00-1号试样类似,裂纹扩展栅丝R1到栅丝R21时,裂纹扩展速度发生小幅度波动,且裂纹扩展到栅丝R21时,距离圆孔边缘5.1 mm 时,裂纹扩展速度显著增大,并且达到最大值420.07 m/s。而试件#20-3裂纹扩展到R21时距离圆孔12.4 mm;试件#30-2裂纹扩展到R21时距离圆孔20.0 mm;试件#40-2裂纹扩展到R21时距离圆孔27.6 mm;试件#50-3裂纹扩展到R21时距离圆孔35.1 mm,这四组试样裂纹扩展距离圆孔边缘较远,因此裂纹扩展速度没有增大的现象。由此可以分析出,当扩展的裂纹距离圆孔较远时,裂纹扩展速度无大幅度变化,可以认为圆孔对裂纹扩展速度无影响,而裂纹扩展速度的小幅波动是由于PMMA 材料的非均质性和实验误差造成的;当裂纹扩展到圆孔边缘附近时,裂纹扩展速度会显著增大。
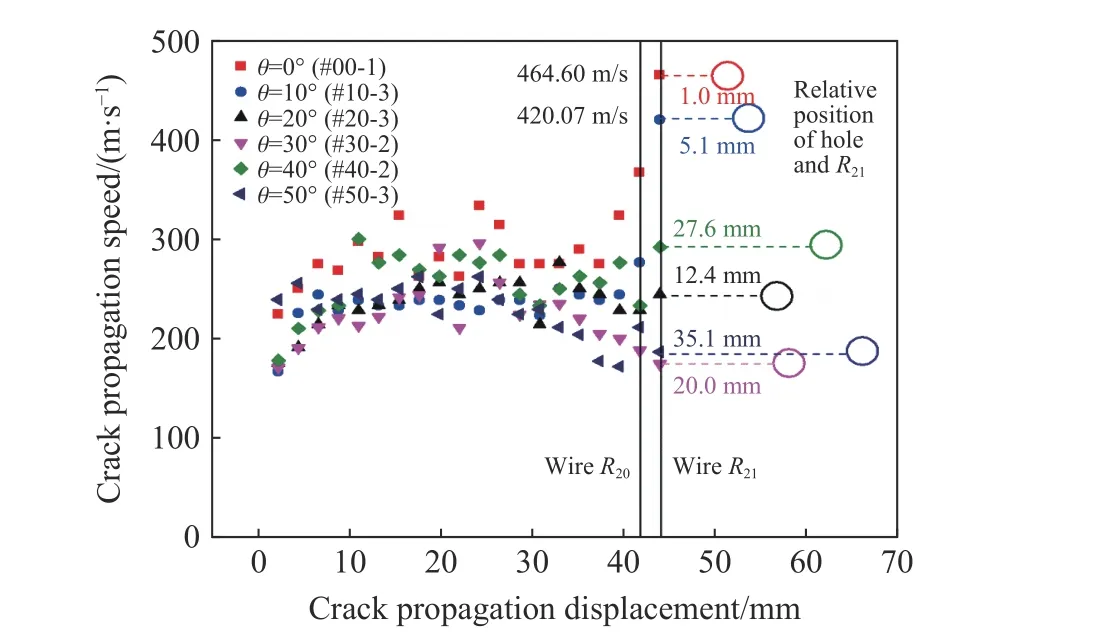
图6 典型试件裂纹扩展速度变化趋势图Fig.6 Trend of crack propagation speed of typical specimens
2 数值模拟
2.1 数值模拟原理简介
本文采用Autody n 软件进行数值模拟来验证实验结果的准确性和分析裂纹扩展的机理。Autodyn 采用有限差分算法,是显式非线性动力分析系统,能够很好地运用于脆性材料在动态载荷下的断裂分析。近年来越来越多的学者运用Autodyn 进行数值模拟研究,并验证了其准确性,如Zhu 等[30-31]、朱哲明等[32]对爆炸载荷下的岩石结构裂纹扩展进行了数值分析,Zhou 等[33]利用Autodyn 模拟了巷道围岩在动载荷作用下Ⅰ/Ⅱ复合型裂纹扩展研究,动态数值模拟结果和动态实验结果非常接近。
构建整体数值模型时,根据冲击实验的边界条件和部件尺寸建立落锤、入射板、试件、透射板及阻尼器,并设立各个部件的实际材料参数,网格采用四面体网格,设定落锤速度初始边界条件为6.0 m/s。数值分析时,为了避免网格的大变形扭曲,采用侵蚀模型(erosion model)。采用最大主应力准则来表征PMMA 材料的动态断裂行为,即:

式中:τmax为材料的最大剪切应力值,τc为材料的最大剪切强度,σ1为材料的最大主应力值,σT为材料的最大拉伸强度。
2.2 数值模拟结果分析
当θ 为0°~50°时的实验结果与数值计算结果对比如图7所示。从裂纹扩展轨迹可以看出,当θ=0°时,裂纹呈直线扩展,到达圆孔上表面后停止扩展,这是由于裂纹到达圆孔上表面后,裂纹尖端的应力集中现象转化为圆孔周围的应力集中现象,这时要让裂纹继续向前扩展需要比原来大很多的断裂能来克服圆孔缺陷所需要的能量;而当θ=10°时,裂纹扩展到圆孔附近时,向圆孔方向发生偏转并到达圆孔表面,表现为圆孔对裂纹具有显著的引导效果;当θ=20°时,裂纹扩展到圆孔附近时,依旧向圆孔缺陷方向发生了偏转,但最终裂纹并未扩展达到圆孔表面,说明圆孔对裂纹的引导效果较θ=10°时要弱一些;当θ=30°时,裂纹扩展出现和θ=20°类似的偏转现象,但相对θ=20°时来说,裂纹偏转的幅度更小,说明θ=30°时圆孔对裂纹的引导效果更小;当θ=40°,50°时,圆孔对裂纹扩展路径几乎没有影响裂纹扩展轨迹不会产生明显的偏折现象,裂纹呈现出明显的纯I 型裂纹扩展行为。总体上来说,动态实验的裂纹扩展轨迹与动态数值模拟结果基本吻合一致,验证与完善了动态实验结果的局限性。

图7 实验结果和模拟结果对比Fig.7 Comparisons of experimental and simulation results
为了分析圆孔使裂纹扩展路径发生偏转的作用机理,以θ=20°的模拟结果为例的试件第一主应力σ1随时间的演变规律如图8所示。从图中可以看出,裂纹扩展的过程中,裂纹尖端和圆孔边缘都会形成很大的第一主应力,随着裂纹扩展靠近圆孔,圆孔边缘的第一主应力逐渐增强,而当裂纹扩展远离圆孔时,圆孔边缘的第一主应力逐渐减小;当裂纹扩展发生明显偏折时(从t=839.3µs开始),裂纹尖端的应力场和圆孔表面的应力场距离较近,使得两拉应力场之间形成较强的应力场,使得裂纹沿着这个拉升应力场方向发生了偏转,最终表现为裂纹扩展向着圆孔方向发生了偏折。
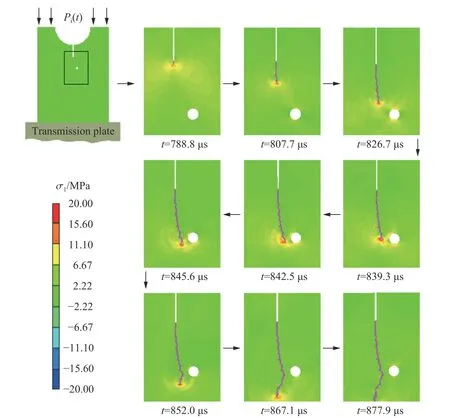
图8 裂纹扩展中的第一主应力云图(θ=20°)Fig.8 Contour mapsof the first principal stress during crack propagation (θ=20°)
PMMA 作为一种脆性材料,它的破坏是由拉应力造成的。因此,本文中根据Autodyn 的模拟结果,计算了距离裂纹尖端1 mm 的环形位置各个网格单元的拉应力方向,即为裂纹尖端的最大周向应力方向,如图9所示,分别计算了不同圆孔偏角时裂纹扩展至圆孔缺陷附近裂纹尖端的最大周向拉应力。从图中可以看出,θ=0°,40°时,在0°方向周向应力是最大的,所以裂纹竖直向下扩展,并未发生偏转;θ=10°时,在54°方向上的周向应力是最大的,因此裂纹沿着54°方向扩展,即裂纹沿着如图7(θ=10°)所示的方向发生了偏转;θ 为20°时,在41°方向上的周向应力是最大的,因此裂纹沿着如图7(θ=20°)所示的方向发生了偏转;θ 为30°时,在4°方向上的周向应力是最大的,因此裂纹沿着圆孔方向轻微的发生了偏转;θ=40°,50°时,在大约0°方向上的周向应力是最大的,因此裂纹并未发生偏转。

图9 裂纹尖端的最大周向应力方向Fig.9 Maximum circumferential stress direction at the crack tip
综合对比各组实验结果和模拟结果可以发现,圆孔偏角θ<10°时,裂纹扩展会达到圆孔,圆孔偏角θ<30°时,圆孔对裂纹扩展具有引导作用,圆孔偏角θ>30°时,圆孔对裂纹扩展几乎没有引导作用。
3 动态断裂韧度计算
采用基于有限元软件Abaqus进行动态应力强度因子的计算,随后结合裂纹扩展计测得的每根栅丝的动态断裂时刻,就可以得到裂纹的起裂韧度和动态断裂韧度,这也是被许多研究学者所采用的实验-数值法[8]。
3.1 有限元数值模型
根据实验的实际尺寸建立数值模型,力学性质材料参数设置根据上文所述的PMMA 材料参数设置,分析步中采用动力隐式计算(dynamic,implicit),因为动力隐式计算能够很好地反映冲击载荷下的瞬时特性。载荷导入实验测得的入射波和透射波,分别加载在模型顶部和底部。裂纹尖端区域采用六节点的三角形CPS6单元,其余网格采用八节点的四边形CPS8单元[14],如图10所示。
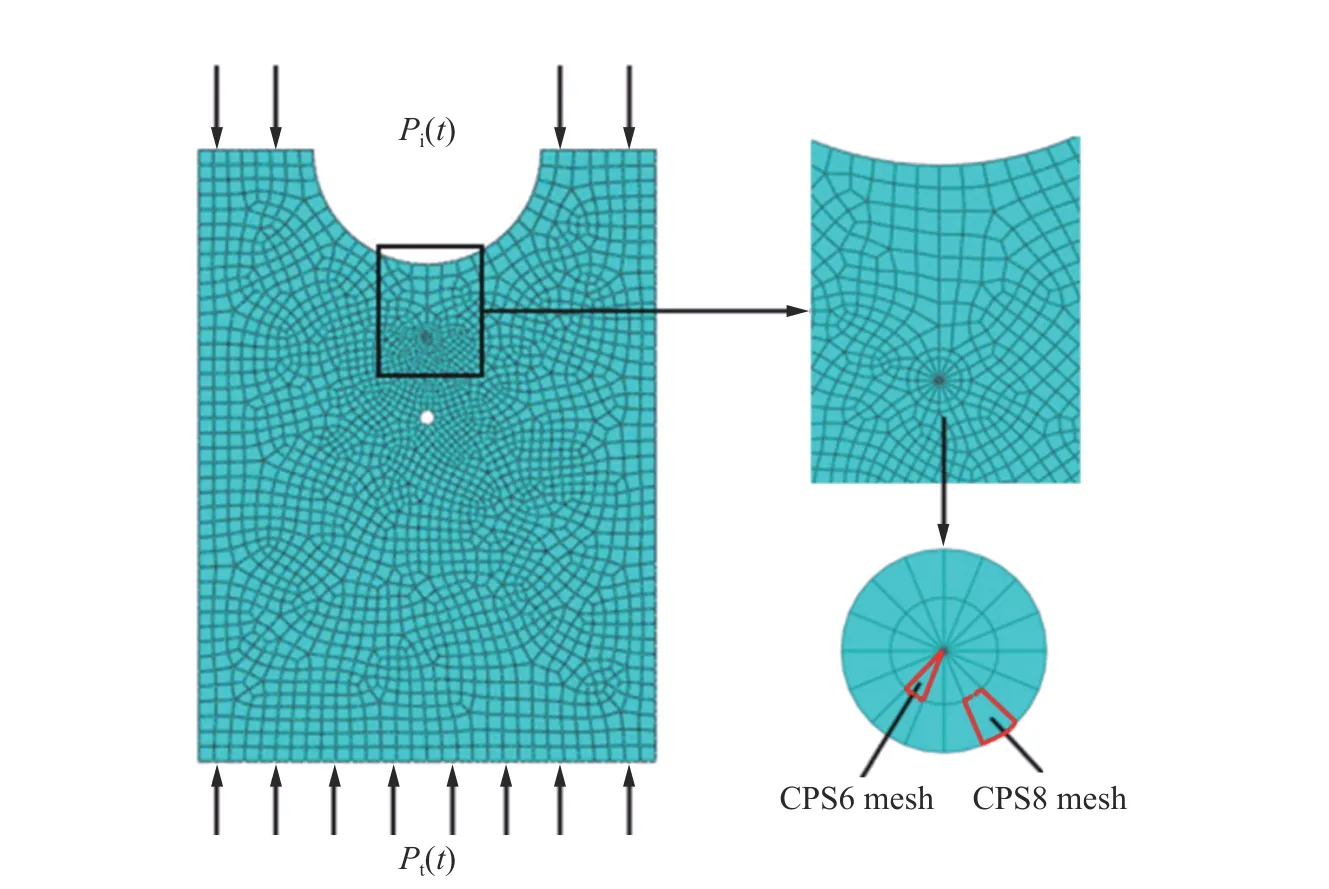
图10 ABAQUS数值模型网格示意图Fig.10 Sketch map of the numerical model in ABAQUS
3.2 动态应力强度因子计算
计算的不同圆孔倾角θ 时裂纹尖端的动态应力强度因子如图11(a)所示,再根据表1的裂纹动态起裂时间,可标定出裂纹的动态起裂韧度,如图11(b)。从图中可以看到,各组式样的裂纹集中在417~427µs之间起裂。在裂纹起裂后,圆孔倾角为θ=0°时的动态应力强度因子的时程曲线值最大,圆孔倾角θ 为10°和20°时次之,倾角为θ=30°、40°及50°时最小,且几乎重合。说明圆孔对裂纹尖端应力强度因子产生影响,当θ 小于30°时,θ 越小裂纹起裂后的裂纹尖端应力强度因子越大,说明θ 大于30°时,圆孔对裂纹尖端应力强度因子几乎没影响。
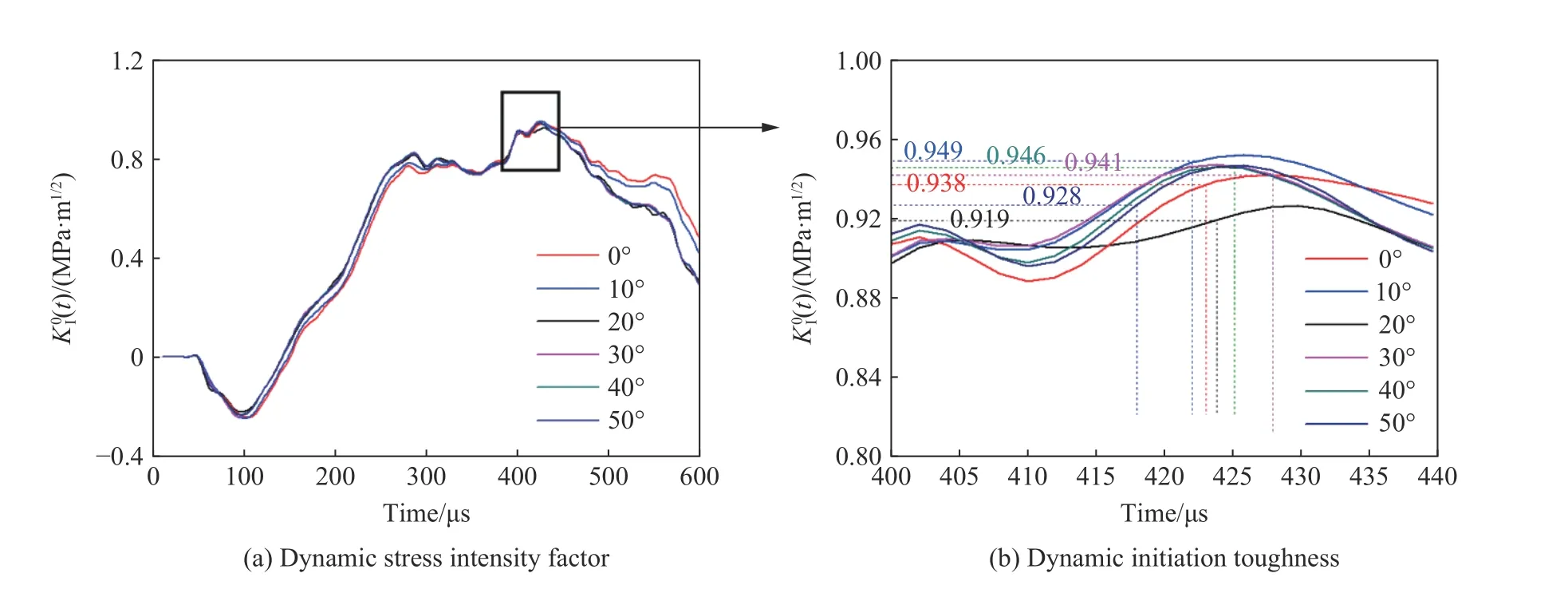
图11 动态应力强度因子时程曲线Fig.11 Histories of the dynamic stress intensity factor
3.3 普适函数修正
Freund[34]认为,裂纹的动态应力强度因子等于该处裂纹静止时的应力强度因子和裂纹扩展的普适函数k(v)的乘积,它表征了裂纹扩展速度对动态应力强度因子的修正函数关系。特别地,对于静止裂纹的临界应力强度因子和动态扩展裂纹的动态断裂韧度也满足普适函数关系,即:


3.4 计算结果分析
以θ=0°为例,用普适函数对静止裂纹的临界应力强度因子进行了修正,如图12(a)所示。可以看出,经普适函数修正后的动态断裂韧度比静止裂纹的临界应力强度因子都要小,这是因为动态裂纹刚开始起裂时裂纹尖端不是理想化的尖锐裂纹,需要克服的起裂阻力较大,当裂纹动态扩展时,裂纹尖端是接近于理想化的尖锐裂纹,克服裂纹起裂的阻力较小。最后计算出各组试样的动态断裂韧度如图12(b)所示,可以看出裂纹初始扩展时的断裂韧度要大于裂纹扩展稳定后的断裂韧度,这是由于裂纹初始扩展时的裂纹扩展速度较小,使得裂纹扩展的惯性效应较弱,所以裂纹扩展的断裂韧度更大;随着裂纹扩展速度趋于稳定,各组试样的动态断裂韧度值也趋于稳定,仅仅发生小幅波动;而对于0°和10°的第21根栅丝位置,由于其紧邻圆孔边缘,其断裂韧度明显减小,这是由于此处的裂纹扩展速度增大,裂纹的惯性效应增大,使得裂纹更易发生扩展。
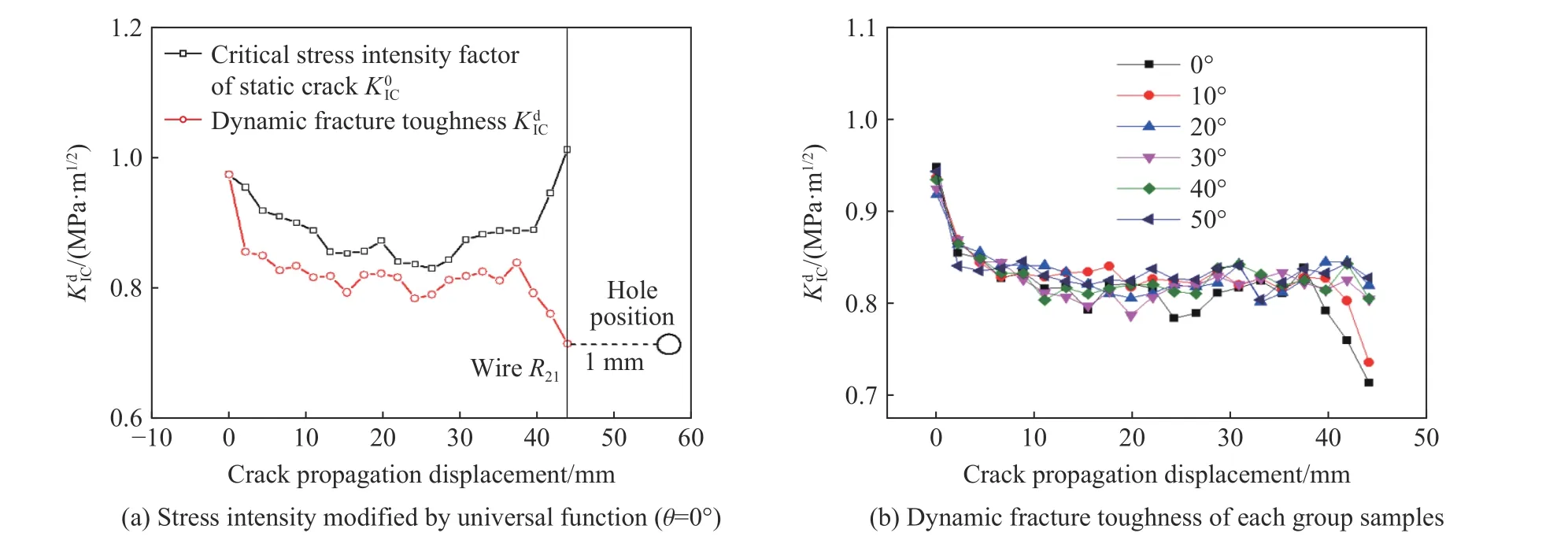
图12 各组试样的动态断裂韧度Fig.12 Dynamic fracture toughness of each specimens
为了验证裂纹动态断裂韧度与裂纹扩展速度之间的关系,对所有试样计算结果的裂纹扩展速度和动态断裂韧度进行了拟合,如图13所示,其中前几个孤立点表示各组试件的起裂韧度,后两个孤立点表示θ=0°,10°的试件裂纹扩展速度显著增加的数据点。根据拟合结果,裂纹动态断裂韧度和裂纹扩展速度关系为=0.9899−0.00055v,决定系数R2达到了0.95775。因此可以说明裂纹扩展速度和动态断裂韧度成负相关关系,即裂纹扩展速度越大,裂纹动态扩展韧度越小。

图13 动态断裂韧度与裂纹扩展速度的关系Fig.13 The relationship between dynamic fracture toughness and crack propagation speed
4 结 论
本文中基于大尺度落锤冲击实验装置对直裂纹空腔圆弧开口试件(COSSCC)进行了动态冲击实验,研究了裂隙试件内圆弧空腔对裂纹扩展轨迹、起裂时刻、裂纹扩展速度及最大周向应力方向的影响规律,采用数值软件Autodyn 分析了裂纹扩展过程中裂尖动态应力场的演变规律,并借助于有限元软件Abaqus 计算了动态断裂韧度随裂纹扩展速度的变化趋势,得出如下结论:
(1)圆孔缺陷对裂隙试件内裂纹扩展轨迹有严重的影响作用。当圆孔相对于裂纹尖端距离一定时,圆孔相对于裂隙的倾角越小,对裂纹扩展的影响越大。当圆孔倾角为10°时,裂纹会向圆孔面进行偏转并到达圆孔面;当圆孔倾角为20°和30°时,裂纹也会继续向圆孔偏转但不会到达圆孔面;当圆孔倾角超过40°以后,圆孔对裂纹扩展轨迹几乎没影响。
(2)COSSCC试件中裂纹扩展到圆孔附近时,裂纹扩展速度会明显增大,裂纹的动态断裂韧度会显著减小。
(3)动载荷作用下裂纹扩展过程中动态扩展韧度不是定值,在逐渐的上下波动,都小于裂纹的动态起裂韧度;裂纹动态断裂韧度与裂纹扩展速度成负相关关系。

