长期持荷工况下钢管混凝土构件的抗撞击性能*
王文达,陈振福,纪孙航
(兰州理工大学土木工程学院,甘肃 兰州730050)
钢管混凝土结构在超高层建筑、大跨桥梁、地铁站台等工程中的应用日益广泛。该类结构柱在承受持续荷载的生命周期内,易遭受一些发生概率低但危害极大的偶然荷载作用,严重威胁人们的生命和财产安全,撞击荷载便是较为常见的一种。2012年阿根廷一辆列车脱轨撞到站台柱,造成49人死亡,600余人受伤[1]。服役中的钢管混凝土柱遭受撞击荷载时,普遍存在一个共同的特点—受到撞击前往往会经历长期持荷的过程,此过程中核心混凝土产生收缩、徐变、刚度退化,导致外钢管和核心混凝土应力重分布。已有较多研究成果表明,长期荷载作用对钢管混凝土构件的静力力学性能有一定的不利影响[2-3],但长期荷载作用对CFST(concrete-filled steel tubular)构件遭受撞击等动力荷载的影响鲜有报道。
目前,对CFST 构件抗撞击性能的研究主要以一次加载为主。Wang 等[4]进行了轴向荷载作用下CFST构件的侧向撞击试验,并建立了有限元分析模型。王潇宇等[5]进行了CFST构件的柱式撞击试验,提出一种CFST柱抗撞击承载力计算方法。Bambach[6]基于目前CFST构件抗撞击性能研究现状,提出构件抗撞击承载力的两种刚塑性计算方法。Yang 等[7]进行了钢管可再生混凝土构件的撞击试验,并与普通CFST构件的抗撞击性能进行了对比。Han 等[8]对大截面圆形钢管高强混凝土构件进行了撞击试验,建立了适应高强混凝土的有限元分析模型。史艳莉等[9]建立了高温下CFST 构件遭受侧向撞击的有限元模型,对构件在高温作用下的抗撞击性能进行了分析。Xian 等[10]、史艳莉等[11-12]、朱翔等[13]、Wang 等[14-15]进行了新型复合截面CFST 构件的撞击试验,分析了不同参数对构件抗撞击性能的影响。亦有学者对CFST 构件撞击后的剩余承载力进行研究,章琪等[16]通过对CFST构件撞击后的承载力进行有限元计算,拟合了撞击后的剩余承载力计算公式。Hou 等[17]分析了多种工况耦合下CFST 构件遭受撞击的破坏模式,对构件剩余承载力进行了计算。Zhang等[18]对侧向撞击后的CFST构件进行了轴向受压承载力试验。上述研究鲜有考虑长期荷载作用对构件抗撞击性能的影响,亦没有对构件从遭受撞击到撞击后继续持荷的过程进行完整分析,对构件抗撞击性能的评价主要以撞击过程中的冲击力时程、位移时程为指标,没有联合考虑钢管混凝土柱作为主要承重构件在撞击后的剩余受压承载能力,而承重构件在撞击后的剩余承载能力则是构件抗撞击性能的主要表现之一,并且物理意义明确。长期荷载作用对CFST构件的静力力学性能较一次加载模式存在差异,因而长期荷载作用对CFST 构件的抗撞击性能可能有一定影响,所以有必要对考虑长期荷载作用的CFST构件的抗撞击性能进行进一步研究。此外,对构件撞击以及撞击后的持荷过程进行完整分析也将更符合构件实际的持荷工况。
本文中,利用ABAQUS建立了长期荷载作用下CFST构件遭受撞击荷载的有限元模型以及构件撞击后的剩余承载力计算模型,对构件在撞击荷载作用下的动力响应和撞击后的承载力进行分析,体现了构件在生命周期内进行多工况耦合受力性能分析的一种思路。将撞击后的剩余受压承载力作为构件抗撞击性能的一个评价指标,可以更加全面地反映构件的抗撞击能力。同时与一次加载模式下构件的抗撞击性能进行了对比,量化分析两种加载模式下构件遭受撞击荷载的动力响应,以期为工程设计提供参考。
1 长期荷载作用下构件遭受撞击荷载的过程
CFST柱在服役期内可能经历多种持荷工况,撞击荷载作用时可能存在的一种持荷过程[17]如图1所示。在施工阶段(图1(a)),钢管首先承担由施工产生的荷载Ns0。施工完成,构件进入正常使用阶段(图1(b)),此时钢管和核心混凝土共同承受荷载N0。在服役期内,构件进入长期持荷阶段(图1(c)),在荷载N0作用下,随着时间的推移,核心混凝土发生收缩、徐变和刚度退化,核心混凝土和钢管发生应力重分布。在正常使用阶段的某个时刻(图1(d)),构件遭受偶然的横向撞击荷载,使构件同时受到轴向荷载N0和侧向撞击荷载的作用。撞击后构件进入继续承受轴向荷载的阶段(图1(e)),构件剩余受压承载力Nd可能大于N0,在修复后可继续使用,也可能小于N0,构件发生破坏。

图1 钢管混凝土柱持荷过程Fig.1 Load history of a concrete filled steel tubular column
对CFST柱考虑长期荷载作用时其加载路径可用一个三维坐标表示,如图2所示,图2中OS、SA、AB、BC、CD(CD´)过程分别与图1中的(a)、(b)、(c)、(d)、(e)等5个阶段相对应。将坐标(x,y,z)分别定义为横向撞击力(F)、时间(t)、轴向压力(N)。当CFST 柱经过图1(a)、(b)两个阶段,轴向荷载达到N0时,构件开始正常服役。随着时间的推移,构件轴向荷载不变,核心混凝土发生收缩、徐变,钢管及核心混凝土进行内力重分布(图1(c))。在某个时刻t1,构件遭受不在轴力作用平面内的侧向撞击荷载,侧向撞击力迅速达到峰值P点(Fp,t2,N0),然后发生衰退,轴向荷载在N0附近上下波动(图1(d))。在整个撞击阶段(图1(d))中,构件始终承受轴向荷载以及横向撞击荷载,两个方向的荷载同时对构件做功。遭受撞击后构件继续持荷(图1(e)),构件的剩余受压承载力可能大于N0,达到D点,在修复后继续使用;亦可能小于N0,达到D′点,发生破坏。本文中将利用有限元软件ABAQUS对AB、BC、CD过程进行计算,并对构件的撞击过程以及撞击后的剩余受压承载力(即BC、CD)进行分析。
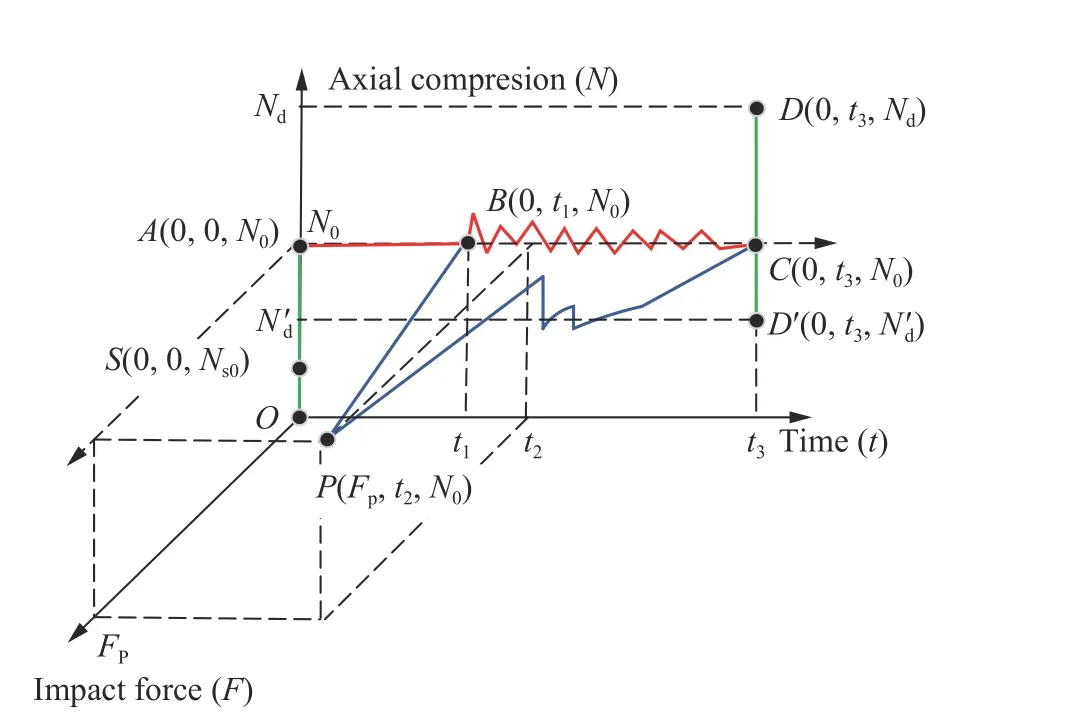
图2 考虑长期荷载作用时构件加载路径示意图Fig.2 A schematic loading path of the concrete filled steel tubular column bearing a long-term load
2 有限元模型
采用ABAQUS对构件在长期荷载作用下遭受撞击荷载的动力响应进行分析,并进行剩余受压承载力计算。整个计算过程需要准静态隐式求解(收缩徐变计算)到动态显式求解(撞击荷载计算)再到静态隐式求解(剩余受压承载力计算)的结果传递,动态分析向静态分析传递时的初始不平衡力可能会产生收敛性问题,可让初始不平衡力在静态隐式计算第1步中线性消失,此过程采用较小的初始增量步(10−4~10−5s)可取得良好的收敛效果。模拟过程分为3步进行:(1)在构件上施加轴向荷载,利用自定义子程序UMAT完成核心混凝土收缩徐变的计算;(2)采用弹簧单元(*Spring)保持构件轴向荷载不变,对构件施加侧向撞击荷载;(3)用位移加载的方式,计算构件的剩余受压承载力。在每一步的衔接中,保持构件单元类型、单元网格划分不变,采用*Input 命令将前一步的计算结果*Res文件导入下一步中。
2.1 材料本构关系
钢材的本构关系采用弹塑性模型,其应力-应变关系采用二次塑流模型[19]。计算撞击荷载时应考虑钢材动力加载所导致的应变率效应[20],根据以往的数值研究,采用Cowper-Symonds模型计算钢材在不同应变率下的屈服强度:

式中:ε˙为钢材的应变率,σd为钢材应变率为 ε˙时的应力值,σs为钢材在静力下的应力值,G和p为材料参数,取G=6 844 s−1,p=3.91。
长期荷载作用下核心混凝土的收缩与徐变理论模型采用ACI209 模型[21],该模型中混凝土徐变系数φ(t,τ)的表达式为:

式中:φmax(τ0)为徐变终值系数,t为持荷时间,τ0为加载龄期。
该模型中混凝土收缩应变计算公式为:

式中:tsh为干燥时间,(εsh)max为干燥收缩最终值。
由于ABAQUS本构库中没有CFST构件核心混凝土的收缩和徐变计算模型,本文采用自定义子程序UMAT 建立核心混凝土在长期荷载作用下的收缩和徐变本构模型,使用ABAQUS子程序接口实现用户自定义本构模型和主求解器之间的数据交换。
核心混凝土在进行撞击荷载计算以及剩余受压承载力计算时,本构关系采用塑性损伤模型。考虑长期荷载作用效应时,对一次加载时核心混凝土单轴受压应力-应变关系模型进行修正[19]:保持应力坐标值不变,将一次加载模式下应变ετ0进行放大平移,得到长期荷载作用时钢管混凝土的应变εt,即εt=[1+φ(t,τ)]ετ0+εsh。一次加载模型与考虑长期荷载作用的核心混凝土应力-应变关系模型如图3所示。本文研究的撞击属于低速撞击的范畴,混凝土的应变率效应并没有钢材表现明显,且长期荷载作用下混凝土的应变率效应缺乏相关研究,因此本文暂不考虑混凝土的应变率效应。由下文中的模型验证可知,不考虑混凝土的应变率效应时,对一次加载模式的侧向撞击试验进行模拟时仍取得了较好的计算结果。

图3 考虑长期荷载作用与否的混凝土应力-应变关系Fig.3 Stress-strain curves of concrete with and without long-term loading
2.2 模型单元选取
核心混凝土采用三维实体单元(C3D8R),钢管采用壳单元(S4R),落锤采用三维离散刚体单元(discrete rigid),混凝土与端板采用Tie绑定,钢管与端板采用壳实耦合。采用弹簧单元(*Spring)为构件施加长期荷载N0,主要有2 个目的:(1)目前一次加载模式下的撞击试验多采用弹簧施加轴向荷载,采用相同的荷载条件有利于进行一次加载模式和考虑长期荷载作用时的对比分析;(2)确保构件受到侧向撞击荷载时有稳定持续的轴向荷载存在。
在钢管-混凝土以及钢管-落锤界面采用“通用接触”,接触属性为:所有接触面法向采用硬接触,即垂直于接触面的压力可以在界面上完全传递;切向采用库伦摩擦模拟界面切向力的传递,其中钢管与混凝土界面库伦摩擦因数为0.6,钢管与落锤界面库伦摩擦因数为0[19]。构件进行撞击荷载计算时进行了网格试验,保证沙漏能控制在总能量的5%以内,构件网格划分及边界条件示意图如图4所示,图中ux、uy、uz分别为x、y、z方向的位移,θx、θy、θz表示绕x、y、z轴的转角。
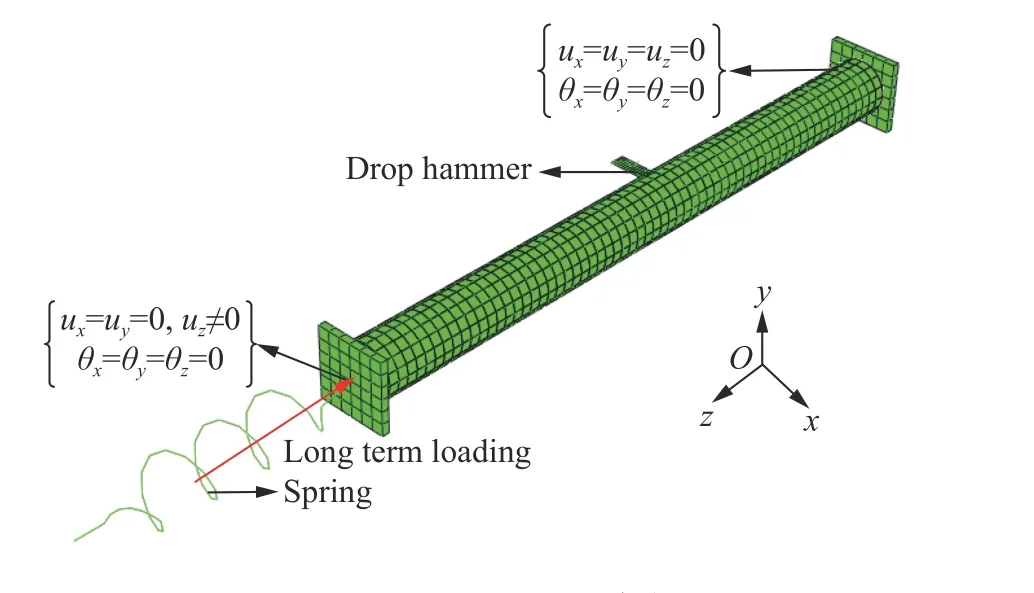
图4 网格划分及边界条件Fig.4 Boundary conditions and element division
3 模型验证
目前缺少CFST构件考虑长期荷载的撞击试验,本文中采用分段验证的方式对有限元模型进行验证。分别对一次加载模式下构件的撞击试验、长期荷载作用下构件的承载力试验、H型钢构件撞击后剩余受压承载力试验进行有限元模型验证。一次加载模式下构件遭受撞击荷载的有限元分析模型包括了施加轴向荷载和撞击荷载两个部分,考虑长期荷载作用时唯一的区别在于施加轴向荷载后进行了收缩和徐变计算,两种加载模式利用ABAQUS进行有限元计算的方法并无本质区别,所以分段验证有限元模型在理论上可行。
3.1 撞击试验有限元模型验证
为验证模型具有普遍性,选取文献[7-8,13]中具有不同边界条件、撞击能量、轴压比n、试件形状、试件尺寸的试验数据进行模型验证,验证内容主要包括撞击力时程曲线、跨中最大挠度、撞击时间。表1给出了试验构件的基本参数,表中d为圆钢管混凝土构件的直径,b为方钢管混凝土构件的边长,δa为钢材厚度,l为构件长度,m为落锤质量,v为冲击速度。
图5和图6分别给出部分构件试验和计算的撞击力(F)时程曲线和跨中位移(Δ)时程曲线对比,可见试验与计算曲线整体变化趋势一致。表1中给出了撞击时间的实测值(tc)与计算值(te)的比值,最大挠度的实测值(Δc)与计算值(Δe)的比值,所有试件tc/te的平均值为1.07,Δc/Δe的平均值为0.99。图7为构件NC-0.3-6跨中位置遭受侧向撞击后试验与数值模拟的破坏形态对比图,图中箭头所指的是构件产生的鼓曲变形,可见计算结果与试验结果吻合良好。
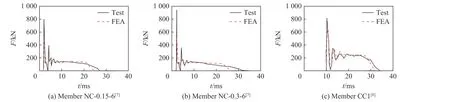
图5 钢管混凝土构件撞击试验与计算撞击力时程曲线对比Fig. 5 Comparison of impact force-time history curves of concrete-filled steel tubular members between tested and calculated results

图6 钢管混凝土构件撞击试验与计算位移时程曲线对比Fig.6 Comparison of displacement-time history curvesof concrete-filled steel tubular members between tested and calculated results

图7 构件NC-0.3-6 试验与模拟破坏形态对比[7]Fig.7 Comparison between tested and calculated failure modes of member NC-0.3-6[7]
3.2 长期荷载作用下构件的承载力试验模型验证
选取文献[22]中具有不同长期荷载比(n)、长细比(λ)的6组CFST构件进行模型验证,构件尺寸d(mm)×δa(mm)×l(mm)、长期荷载比(n)、长细比(λ)在图8中列出,构件持荷时长为462 d,构件的轴向荷载(Fa)-应变(ε)关系曲线的试验与计算结果对比如图8所示,可见试验结果与数值模拟吻合良好。

图8 钢管混凝土构件轴向荷载-应变关系曲线试验与计算结果对比[22]Fig.8 Comparison of load-strain curves of CFST members between tested and calculated results[22]
3.3 钢构件撞击后剩余承载力试验模型验证
对文献[23]中在撞击时具有不同撞击高度、边界条件的H 型钢构件在撞击后的剩余承载力试验进行计算,H 型钢构件的型号为HW100×100×6×8,长度为1500 mm。图9为两组构件的轴向荷载(Fa)-位移(Δa)关系曲线。由图9可知,两组构件的荷载-位移关系曲线试验与计算结果变化趋势一致,计算的极限承载力与试验的极限承载力的比值分别为1.05、0.98,表明数值计算结果良好。

图9 H 型钢构件荷载-位移曲线试验与计算结果对比[23]Fig.9 Comparison between tested and calculated curves of load-displacement of H-section steel members[23]
4 长期荷载作用下与一次加载模式下构件遭受撞击荷载的全过程对比分析
建立圆形CFST 构件在长期荷载作用下遭受横向撞击荷载的有限元分析模型,构件参数为:构件长度为1800 mm,钢管外径为160 mm,壁厚为4 mm,钢材屈服强度为235 MPa,混凝土强度等级为C50,长期荷载比(轴压比)为0.4,持荷时间为365 d,落锤质量取600 kg,撞击速度为5 m/s。
4.1 撞击力时程曲线对比和位移时程曲线对比
一次加载模式与考虑长期荷载时构件的撞击力时程曲线和跨中位移时程曲线以及撞击力-跨中位移曲线如图10所示。由图10(a)可知,与一次加载模式相同,长期荷载作用下撞击力时程曲线也可以分为峰值段、平台段、卸载段3个阶段[4],在峰值段结束后,撞击力存在一个2 ms左右的零值段,零值段的存在与构件侧向刚度大小有关,而侧向刚度主要受边界条件和长细比等因素的影响,当撞击发生的瞬间构件获得较大速度,以大于落锤的速度向下运动,导致构件和落锤发生短暂分离。但考虑长期荷载时,撞击力峰值下降34.7%,撞击力平台值下降11%,撞击时间延长12.4%,零值段的时间延长。其原因在于核心混凝土截面刚度降低,导致组合截面的刚度下降,使构件的线刚度减小。由图10(b)可知,在0.015 s之前两种加载模式下构件跨中位移随时间变化的差异很小,相同时刻下考虑长期荷载时的位移比一次加载模式增加1~2 mm。在0.015 s 之后两种加载模式下构件跨中位移随时间变化的差异逐渐增大,构件跨中最大位移较一次加载模式增加10.9%。

图10 撞击力和位移时程曲线以及撞击力与跨中位移关系曲线Fig.10 Time history curves of impact and displacement aswell as relation of impact force and displacement
利用数据分析软件ORIGIN 中的曲线积分功能,撞击力分别对撞击时间和构件跨中位移进行积分。通过图10(a)计算一次加载模式下撞击力冲量为3 494 N∙s,长期荷载作用下撞击力冲量为3 465 N∙s。通过图10(c)计算一次加载模式下撞击力做功7 540 J,长期荷载作用下撞击力做功7 476 J。可见考虑长期荷载时,虽然冲击力峰值和平台值都减小,但撞击力冲量和撞击力做功较一次加载模式只下降了0.83%和0.85%,所以撞击力冲量和撞击力所做的功与一次加载模式基本相同,但构件的变形增大。
4.2 撞击过程能量变化对比
在撞击荷载作用下,构件的塑性变形为其主要耗能方式[4],两种加载模式的撞击过程,外荷载对构件所做的功主要有两部分:一部分是落锤动能,另外一部分为轴力沿轴向位移所做的功。对外荷载所做的功进行叠加计算,考虑长期荷载时外荷载对构件所做的功比一次加载模式增加了7.2%。图11为一次加载模式与考虑长期荷载时构件的塑性耗散能时程曲线和落锤动能时程曲线,可见长期荷载作用下外钢管塑性耗能显著增大,而落锤动能差异很小,所以外荷载做功增加的部分主要来自轴向荷载。计算可知长期荷载作用下轴向荷载所做的功比一次加载模式增加13.9%,核心混凝土的塑性耗散能增加0.84%,钢管的塑性耗散能增加12.6%。所以考虑长期荷载作用时轴向荷载做功增加的部分主要通过外钢管的塑性变形耗散,核心混凝土贡献较小。

图11 落锤动能以及构件各部分塑性耗散能时程曲线Fig.11 Time history curvesof kinetic energy of drop hammer and energy dissipation of the components of CFST members
4.3 构件轴向荷载-位移曲线对比
通过数值模拟,构件在本文研究时的加载机制下的轴向荷载-位移曲线如图12所示。结合图2构件的加载路径,长期荷载作用下构件轴向荷载-位移曲线经历了OA、AB、BC、CD等4 个阶段。在撞击前,构件经过OA阶段开始服役,长期荷载作用下(AB段)构件持荷大小不变,轴向位移增加,而一次加载不会经历这个过程。在撞击过程中(BC段),两种加载模式下构件轴向荷载在0.4的长期荷载比(轴压比)上下波动,但长期荷载作用下构件的轴向位移较一次加载模式增加18.3%。轴向位移增大的原因主要考虑两个方面:长期荷载使构件的核心混凝土发生收缩徐变,刚度退化;此条件下撞击荷载引起的构件跨中挠度增大,从而二阶效应较一次加载模式显著。构件在撞击后继续承受轴向荷载(CD段),可见一次加载模式下构件的剩余受压承载力为584 kN,长期荷载作用下构件的剩余受压承载力为540 kN,考虑长期荷载时构件的剩余受压承载力较一次加载模式下降7.5%,原因在于构件受到长期荷载的影响,而且二阶效应较一次加载模式显著。
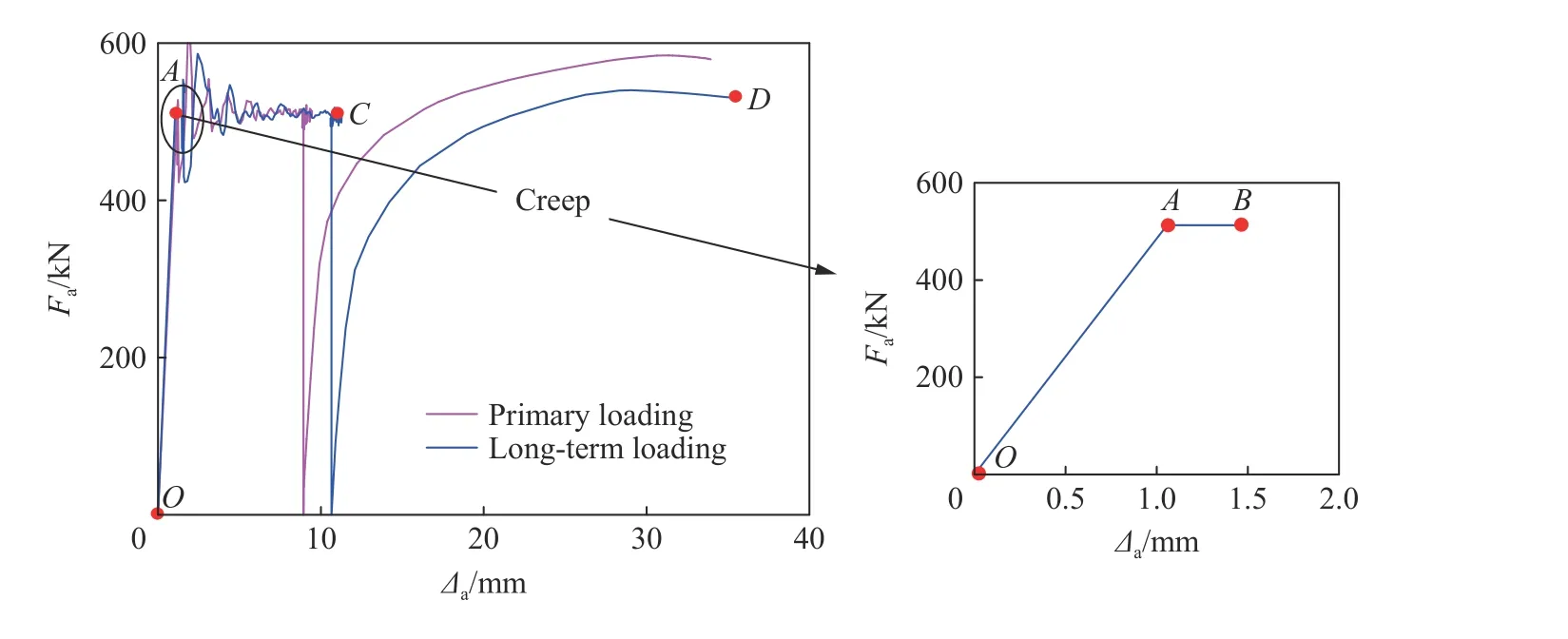
图12 钢管混凝土构件轴向荷载-位移曲线Fig.12 Axial load-displacement curvesof CFST members
5 不同参数下长期荷载对构件抗撞击性能的影响
以第4节中的有限元模型为基础,保持落锤质量和速度不变,对比CFST构件考虑长期荷载时与一次加载模式下的抗撞击性能,长期荷载持荷时间为365 d。参数包括长期荷载比(轴压比n)、混凝土强度(fcu)、钢材屈服强度(fy)、长细比(λ)、含钢率(α)。构件的抗撞击性能主要以跨中极限挠度,剩余受压承载力系数衡量。跨中极限挠度(Δmax)被定义为撞击过程中构件跨中产生的最大挠度,定义剩余受压承载力系数k,如下式:

式中:Nd为撞击后的受压承载力峰值,Nu为构件撞击前不考虑长期荷载作用的轴心受压承载力。剩余受压承载力系数k可反映构件剩余承载力大小,同时可与长期荷载比n(n=N0/Nu)通过比较数值大小直观反映构件在撞击后是否发生破坏,所以可以作为构件抗撞击性能评价的一个指标。
5.1 长期荷载比
选取长期荷载比(轴压比)n为0.3、0.4、0.5,对两种加载模式下构件的抗撞击性能进行对比。图13给出了不同长期荷载比(轴压比)时构件在撞击荷载作用下的跨中极限挠度以及撞击后的剩余受压承载力系数(k)。由图13(a)可知,随着长期荷载比n增大,跨中极限挠度逐渐增大,但考虑长期荷载作用时,相同条件下构件跨中极限挠度较一次加载模式差异明显。长期荷载比n为0.3、0.4、0.5时、构件跨中极限挠度较一次加载分别增加4.7、6.6、7.8 mm,这种差异随着轴向荷载的增大而增大。由图13(b)可知,随着长期荷载比n的增大,构件在撞击后的剩余受压承载力系数逐渐降低,一次加载模式下的撞后剩余受压承载力明显高于考虑长期荷载作用的结果,长期荷载的影响随着长期荷载比n的增大而增大。值得注意的是,长期荷载比n为0.4时,若按照一次加载模式分析,构件遭受撞击后k大于0.4,可继续承载,但是考虑长期荷载作用,构件遭受撞击后k小于0.4,则会丧失承载能力。以上分析表明随着长期荷载比n的增大,长期荷载对构件的抗撞击性能较一次加载模式影响愈大,适当减小长期荷载比n,有利于减小长期荷载对构件抗撞击性能的不利影响。

图13 不同长期荷载比下跨中极限挠度及剩余受压承载力系数Fig.13 The mid-span deflections and residual compressivestrength coefficients at different long-term load ratios
5.2 混凝土强度
混凝土强度fcu采用30~80 MPa,n为0.4。图14(a)为两种加载模式下构件撞击后的跨中极限挠度,可见随着混凝土强度的提高,跨中极限挠度逐渐降低。混凝土强度相同时,长期荷载作用下构件跨中极限挠度增大,混凝土强度较低时差异愈大,混凝土强度为30和80 MPa 时,构件跨中极限挠度比一次加载模式分别增加21.1%和8.4%。此外,一次加载模式下混凝土强度对构件的跨中极限挠度影响并不明显,文献[4]和文献[8]中亦给出了相似结论,但是考虑长期荷载时,跨中极限挠度随混凝土强度变化的趋势明显变得陡峭,可见考虑长期荷载时混凝土强度对构件跨中极限挠度的影响增加。图14(b)为两种加载模式下构件在撞击后的剩余受压承载力系数(k),随着混凝土强度的提高,剩余受压承载力系数下降。混凝土强度相同时,长期荷载作用下构件的剩余受压承载力系数均比一次加载模式下降0.1左右。一次加载模式下,混凝土强度为30~60 MPa 时,k均大于0.4的轴压比,构件可继续承载,但考虑长期荷载作用时,k均低于0.4的长期荷载比,构件丧失承载能力。随着混凝土强度的提高,k却逐渐降低,这是由于提高混凝土强度显著提高了构件的轴心受压承载力,而对构件的弯剪承载力贡献不大,撞击荷载作用下构件主要以弯剪破坏为主,构件遭受撞击后继续承载时弯曲破坏对构件的承载力起控制作用。

图14 不同混凝土强度下跨中极限挠度及剩余受压承载力系数Fig.14 The mid-span deflections and residual compressivestrength coefficients at different concrete strengths
5.3 钢材屈服强度
分别对钢材屈服强度fy为235、345、420 MPa 时两种加载模式下构件的撞击过程及撞后剩余受压承载力进行计算,n为0.4。图15给出了不同钢材屈服强度下构件的跨中极限挠度及剩余受压承载力系数(k)。由图15(a)可知,随着钢材屈服强度的提高,构件跨中极限挠度逐渐降低。与一次加载模式相比,考虑长期荷载时构件在同等钢材强度下跨中极限挠度增加。钢材屈服强度为235 MPa 和420 MPa 时跨中极限挠度比一次加载模式分别增加10.9%和8.7%,所以差异随着钢材屈服强度的提高而减小。由图15(b)可知,随着钢材屈服强度的提高,构件的剩余受压承载力系数逐渐增大。钢材屈服强度相同时,与一次加载模式相比,长期荷载作用下k均有不同程度下降,钢材屈服强度为235 MPa 时k下降幅度可达20.7%。值得一提的是,提高混凝土强度和钢材屈服强度均可提高构件撞击前的轴向受压承载力,但提高混凝土强度,构件剩余受压承载力系数降低,而提高钢材屈服强度可有效提高构件的剩余受压承载力系数,其原因在于钢材屈服强度的提高可以显著提高构件的抗弯和抗剪性能。
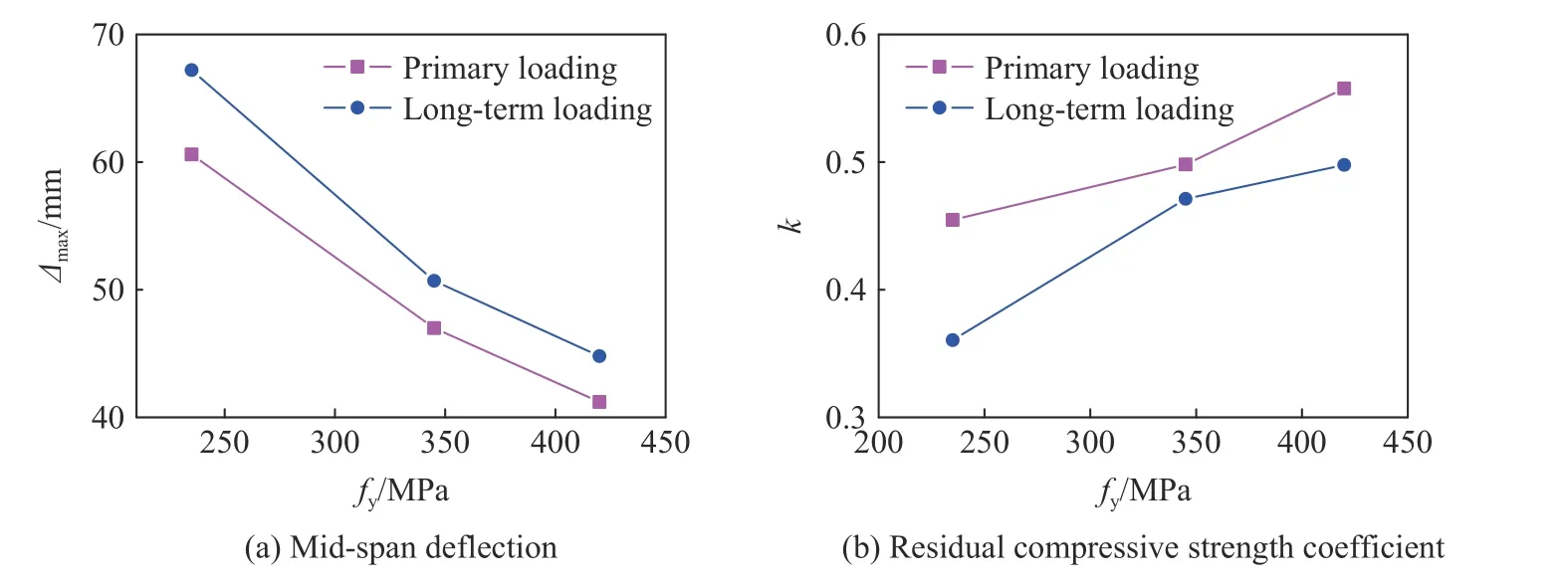
图15 不同钢材屈服强度下跨中极限挠度及剩余受压承载力系数Fig.15 The mid-span deflections and residual compressive strength coefficients at different steel yield strengths
5.4 长细比
n为0.4,对比长细比λ 为20、45、70时构件在两种加载模式下的抗撞击性能。图16给出了不同长细比对应的跨中极限挠度及剩余受压承载力系数(k)。由图16(a)可知,随着长细比的增大,构件跨中极限挠度逐渐增大,长期荷载作用下构件跨中极限挠度较一次加载模式上升。长细比为20和70时跨中挠度较一次加载模式分别增加2.5%和21.4%,可见差异随着长细比的增大而增大。由图16(b)可知,随着长细比的增大,构件剩余受压承载力系数减小,考虑长期荷载的计算结果较一次加载模式均有所降低。但与跨中挠度的变化规律不同,随着长细比的增大,长期荷载作用下与一次加载模式下剩余受压承载力系数k之间的差异减小,λ 为20和70时k分别比一次加载模式下降18.3%和11.7%。原因在于随着长细比λ 的增大,遭受撞击后构件的二阶效应增强,此时构件不再发生材料破坏,几何因素起主导作用,整体失稳和局部失稳为其破坏特征。
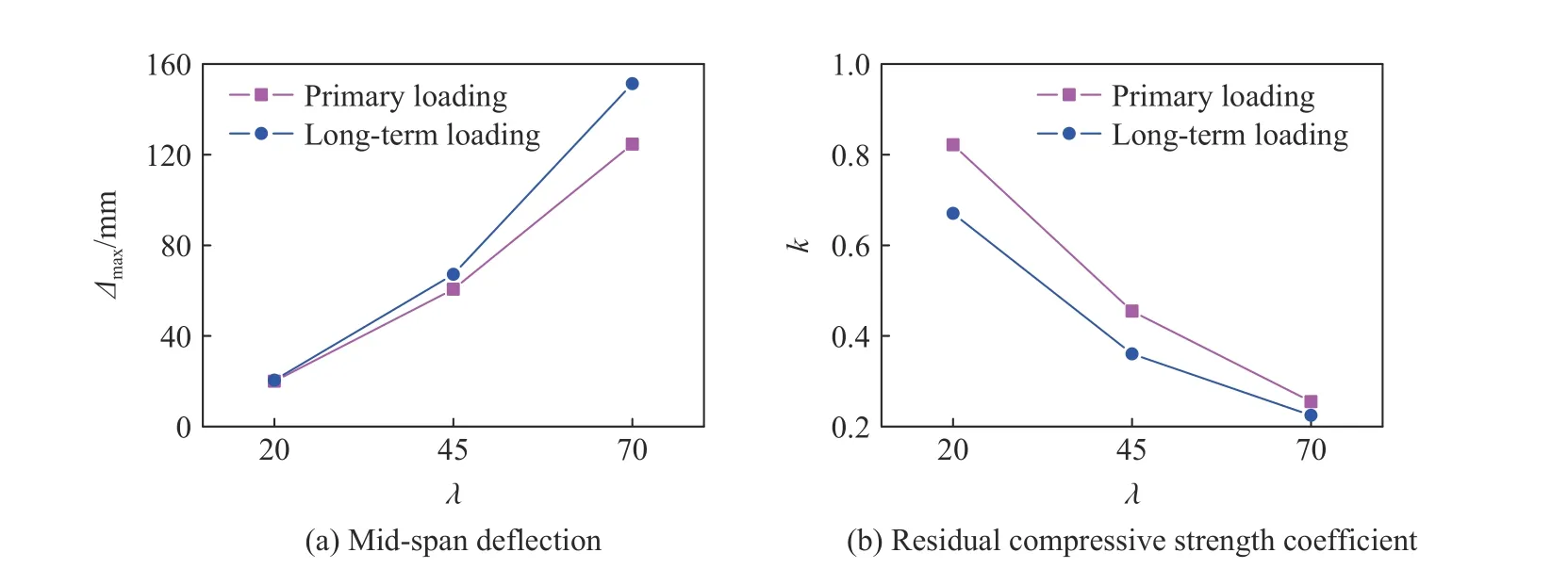
图16 不同长细比下跨中极限挠度及剩余受压承载力系数Fig.16 The mid-span deflections and residual compressivestrength coefficients at different slenderness ratios
5.5 含钢率
保持构件直径不变,通过变化钢管厚度来改变构件的含钢率α,分别对含钢率α 为0.4、0.8、0.12、0.16、0.2的构件进行计算,n为0.4。图17(a)为两种加载模式下构件撞击后的跨中极限挠度,可以看出,随着含钢率α 的提高,构件跨中极限挠度减小。长期荷载作用下,含钢率α 为0.04和0.20时构件跨中极限挠度比一次加载模式分别增加22.4%和9.9%,可见随着含钢率α 的提高,两种加载模式跨中极限挠度存在的差异减小。图17(b)为两种加载模式下构件撞击后的剩余受压承载力系数(k),可见随着含钢率α 的提高,构件的剩余受压承载力系数增大,考虑长期荷载时构件的剩余受压承载力系数低于一次加载模式。含钢率α 为0.04和0.20时剩余受压承载力系数k比一次加载模式分别下降20.7%和2.0%,差异随着含钢率α 的提高而减小。差异减小的原因在于撞击能量较小时,随着含钢率α 的增大,构件遭受撞击的能量大多被钢管吸收,混凝土并未完全发挥作用,钢管的材料性质在考虑长期荷载时并未发生变化,构件撞击后的损伤程度和一次加载模式差异很小。以上分析表明提高含钢率可以有效改善长期荷载对构件抗撞击性能的不利影响。

图17 不同含钢率下跨中极限挠度及剩余受压承载力系数Fig.17 The mid-span deflections and residual compressive strength coefficientsat different steel ratios
6 结 论
建立了长期荷载作用下钢管混凝土柱遭受侧向撞击荷载的有限元分析模型和撞击后剩余受压承载力计算模型,并对模型的准确性进行了合理的验证。在此基础上,对长期荷载作用下和一次加载模式下钢管混凝土柱的抗撞击性能进行了对比,通过典型的有限元模型对钢管混凝土柱的撞击力时程曲线、位移时程曲线、撞击能量、撞后剩余受压承载力进行分析,主要得到以下结论。
(1)与一次加载模式相比,长期荷载作用下构件撞击力时程曲线的撞击力峰值和平台值下降,撞击时间延长,跨中极限挠度增大,外钢管塑性变形增大,但两种模式下落锤对构件所做的功基本相同。
(2)撞击能量在一定范围内时,长期荷载作用下构件轴向荷载做功比一次加载模式增加,做功增加的能量主要通过外钢管的塑性变形耗散,核心混凝土的贡献很小。
(3)两种加载模式下构件的跨中极限挠度和剩余受压承载力系数变化规律相同;考虑长期荷载作用会增大构件跨中挠度、降低撞击后的剩余受压承载力。
(4)撞击条件相同时,一次加载模式下撞击后可以继续承载的构件在考虑长期荷载作用时可能会丧失承载能力;提高含钢率、降低长期荷载比可以减小长期荷载作用对构件抗撞击性能的不利影响。
(5)提高混凝土强度和钢材屈服强度均可降低构件撞击后的跨中挠度,但随着混凝土强度的提高,剩余受压承载力系数减小,而随着钢材强度的提高,剩余受压承载力系数增大。

