基于数轴模型的“四舍五入”教学实践研究

摘 要：“四舍五入”是求近似数的主要方法，四年级学生求解近似数的错误率居高不下，五年级学生求解小数的近似数错误率更是明显增加。为此，笔者深入分析教材，关注数学知识整体性，借助数轴，帮助学生构建“四舍五入”模型。

关键词：小学数学;数轴;四舍五入

中图分类号：G420                                  文献标识码：A                                       文章编号：2095-9192（2021）07-0028-02

引 言

苏教版四年级下册第二单元呈现了“近似数”和“四舍五入”的概念。中低年级学生已经具备了用四舍五入法求近似数的浅层思维，如“289最接近几百”，但在四年级教材中呈现出用四舍五入法求近似数后，学生却不知如何解决问题。

一、追溯问题本源，探寻解决策略

学生用四舍五入法求近似数出现错误的原因一般有三点。一是数域扩大，认知难度提升;二是机械地利用四舍五入法求解某数的近似数，不清楚为什么要看省略尾数部分的最高位，为什么“四舍”，为什么“五入”;三是教学过于注重方法，忽略了对四舍五入背后隐藏的道理的讲解，忽视了数轴对求近似数的作用。

在苏教版教材中，数轴概念正式出现在七年级，但小学数学教材中经常出现数轴的身影。对小学生而言，数轴的原型是直尺，教材中的呈现先把“数尺”抽象成“数线”，再把“数线”逐渐变为数轴，这样编排符合学生的认知规律，凸显了数轴的作用[1]。

教师应深入理解知识教学，思考面对近似数这一难点应如何设计教学，从而实现提质增效。笔者借助数轴，加深学生对近似数本质的理解，引领学生寻根溯源，探究四舍五入法背后的道理。

二、厘清教材编排体系，找准认知起点

朱乐平老师曾说：“只有精细地研读数学教材，才有可能看到编者闪光的思想。”笔者深挖一至六年级的数学教材，发现低年级涉及近似数的问题中都会出现数轴，形象直观;四年级正式出现近似数和四舍五入法的概念时也穿插了数轴，但在实际教学中并没有充分利用数形结合思想解决实际问题。

为了打通学段边界，帮助学生实现知识迁移，使其把握数学知识的整体性，教师应从低年级开始逐步向学生渗透数形结合思想。

（一）借数轴直观呈现——近似数的含义

图1是苏教版数学一年级上册“期末复习”中的一道练习题，是小学阶段学生首次接触近似数的练习。

“接近几十”既是两位数的近似数的含义，又是求两位数的近似数的思考方法，这个方法可以迁移到求三位数、四位数的近似数。教材中虽然没有强调使用具体的方法进行判断，但实质上渗透了利用四舍五入法求近似数的思想。学生利用数轴，再根据两数之间的距离大小便可作出判断。

（二）借数轴初步感知——求近似数为什么以“5”作为分界点

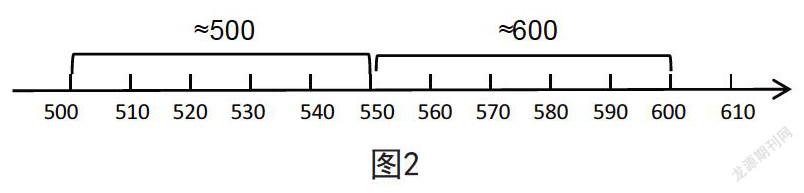
二年级下册教材第四单元出现认识三位数和四位数的内容，第一次在例题中呈现出整数的近似数，没有出现“近似数”这个词，也没有强调用“四舍五入法”求近似数，但首次出现“约等号”，并用它表示近似数。除例题外，教材中安排的“想想做做”，如图2所示，在数轴上表示出500，510，520，…，600，让学生体会哪几个数接近500，哪几个数接近600。

学生通过观察数轴可以发现，以500和600中间数550作为分界点，十位上小于5的数都接近500，十位上等于或大于5的数都接近600，初步体会求一个三位数接近几百需要关注十位。学生在此积累的学习经验，将会有效支撑他们求三位数或四位数的近似数，也为四年级用四舍五入法求近似数打下了基础。

（三）借数轴深入理解——求近似数为什么只看省略部分的最高位

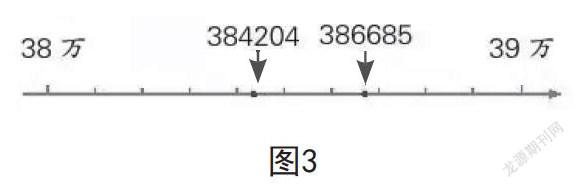
苏教版四年级下册第二单元“认识多位数”中正式引入了“近似数”和“四舍五入法”的概念。在教学中，教师应着重让学生体会画点活动，如图3所示，通过在数轴上画出384204和386685这两个点，体会384204接近38万，386685接近39万，借助认知经验和数轴的直观特点化解教学难点。

教材中“小辣椒”的思考方法直观形象，方法是“384204在385000左边，接近38万;386685在385000右边，接近39万”。“小番茄”的思考相对抽象，方法是“384204千位上是4，比385000小，接近38万;386685千位上是6，比385000大，接近39万”。在教学多位数的近似数时，教师既要引导学生经历像“小辣椒”那样的形象思考，也要总结“小番茄”的经验，以进行抽象思考。

在此基础上，教师应借助数轴，引导学生探究为什么四舍五入求近似数要看省略的尾数部分的最高位，让学生以百以内某数的近似数为起点，体会求两位数接近几十要看个位;再探索千以内的数，发现三位数接近几百需要看十位。初步感知四舍五入后，教师应将研究拓展到万以内的数。例如，根据数轴，找一找接近7000的数有哪些？学生将前面两个问题的探究经验和结论迁移过来，观察数轴可以发现，6500～6999，7001～7499这些数都近似7000，如图4所示，且只需要关注百位上的数即可，六千多的数，百位上是5～9对应“五入”，七千多的数，百位上是0～4（此处7000为精确数，除外）对应“四舍”。将此教学结构迁移到大数的探究中，学生可以得出相同的结论，“四舍五入”的模型已经基本形成。

三、巧用学习正迁移，完善“四舍五入”数轴模型

（一）借数轴自主推理——小数的近似数求解方法

从一年级到四年级，学生完整建构了“整数的四舍五入”模型，随着数域的扩大，求小数的近似数有着相同的思考过程。苏教版五年级上册第三单元“小数的意义和性质”中安排求小数的近似数，笔者利用数轴，深入浅出地剖析小数的近似数求解方法。笔者将数轴中的一小部分进行放大，整数的近似数和小数的近似数构成完整体系。如图5所示，数轴上2.72更接近2.7，2.78更接近2.8，由此可知，2.72保留一位小数是2.7;2.78保留一位小数是2.8。

（二）借数轴深刻体会——小数的四舍五入隐藏的道理

如果小数的位数增多，如2.781，2.785，2.789999，在数轴上画出这三个点后，学生则会很明显地发现虽然小数无限接近2.79，但无论2.78末尾有多少个9，它们仍然比2.79小。从千分位开始数位上的数对精确到十分位并没有影响，即精确到哪一位只需要關注它后面的数位上的数，这也就充分解释了为什么小数的四舍五入法同样需要根据省略尾数部分最高位上的数来判断是“舍”还是“入”。

结  语

小小的数轴中蕴藏着巨大的教学价值，它直观形象地使学生将四舍五入和数在数轴上的位置密切联系起来，能够凸显学生思维中的盲点。学生理解了四舍五入为什么只需看省略的尾数部分最高位的难点，其思维能够更好地从直观形象向抽象概括发展，从而延伸思维的深度和广度，不断培养自身的高阶思维。

[参考文献]

张云萍.依托数轴之形  助力素养提升[J].小学数学教师，2020（04）：79-82.

作者简介：陈娟（1978.11-），女，江苏淮安人，一级教师，曾获区级“学科带头人”、市级“骨干教师”称号。