在数轴上表示不等式的解集

黄日坤

在解不等式时，通常要求在数轴上表示不等式的解集.然而，很多同学在利用数轴表示不等式的解集时，对向右边画还是向左边画以及该使用实心圆点还是空心圆圈搞不清楚.下面请黄老师通过实例介绍一些秘诀。供同学们参考.

例 请同学们在数轴上表示下列不等-式的解集.

（1）z+l>-1.（2）X-2≤1.（3）X+3<4.（4）X≥-2.

解析：首先要求出不等式的解集，然后正确画出图形. （1）解不等式x+l>-I，得x>-2. 把不等式的解集x>-2在数轴上表示出来.如图1所示.

点评：在数轴上，右边的点表示的数总是比左边的点表示的数大，并且不等式的解集中没有等号，因此应该向右边画且用空心圆圈.

（2）解不等式x-2≤1，得x≤3.

把不等式的解集x≤3在数轴上表示出来，如图2所示.

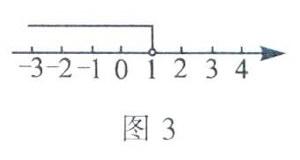
点译：在数轴上，左边的点表示的数总是比右边的点表示的数小，并且不等式的解集中有等号，因此应该向左边画且用实心圆点. （3）解不等式x+3<4，得x<1. 把不等式的解集x

点评：在数轴上，左边的点表示的数总是比右边的点表示的数小，并且不等式的解集中没有等号，因此应该向左边画且用空心圆圈。

（4）把不等式的解集X≥-2在数轴上表示出来，如图4所示.

点译：在数轴上，右边的点表示的数总是比左边的点表示的数大，并且不等式的解集中有等号，因此应该向右边画且用实心圆点.

综上可知，要在数轴上表示不等式的解集，可运用如下秘诀：大于向右边画，小于向左边画，有等号的画实心圆点，无等号的画空心圆圈。