以动探静,变中求定
周凌宇


“认识垂线”是苏教版四年级上册教材“垂线与平行线”单元中的一课时,属于“图形与几何”领域中的“图形的认识”版块。
教学思考:
1.教学的意义在哪里?
本课是学生对于两条直线位置关系的初次探索,学生很容易就能掌握“两条直线相交成直角,这两条直线就互相垂直”;通过测量,也不难发现“点到直线,垂直线段是最短的”。我认为本课的教学意义是让学生在两条直线的运动过程中感受位置关系的变与不变,对相交与互相垂直构建起整体的认识。
2.教学的起点在哪里?
学生对于两条线的位置关系、点到直线的距离,是有一定生活经验的,学生在很多事物上见过交叉的线,但并未抽象到数学层面,仅仅停留在具体的实物上,比如知道两条道路,有的交叉,有的不交叉;也在本单元第一课时中,知道了由一点引出的两条射线可以组成角。因此,本课教学从学生的已有经验入手,在直线运动、变化的过程中,发现相交的变与不变,体会点到直线垂直线段最短。逐步加深对两条直线位置关系的理解,整体构建学生的空间观念。
一、以动探静,构建垂线概念
互相垂直是两条直线相交成直角时的一种特殊情况,那如何体现出垂直的这一特殊性?本环节借助两条相交直线绕着交点的一次动态旋转,将无数种相交的情况作为一个整体来进行教学,由具体到抽象,实现相交与垂直概念的整体建构。
【片段一】
师:根据“挑花棒”的游戏经验,现在只有2根小棒,撒下去,可能出现怎样的情况?(生:相交或不相交。)把小棒看做直线,拿起桌上的2根小棒自己撒一次。刚才大家出现了各种情况的相交。其实,这些相交,我用两条直线,一次就能全演示出来。看!整体不变,但让一条直线放平,然后第二条直线慢慢地旋转(课件演示图1),过程中出现你的那种相交了吗?(生:出现了!)
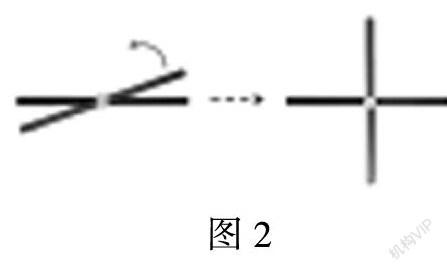
师:其实,在旋转过程中,所有的相交,都有始终不变的地方。(生:中心点不变;角的数量不变,都是4个角。)相交的这个点我们叫做交点。除了有交点,还都有4个角。那有什么是变化的?(生:角度在变。有的角在变大、有的在变小。)那在所有情况中,你认为哪种相交情况最特殊?(生:转到中间时。)请你来转一转(板贴、旋转,图2)。这种情况特殊在哪里?(相交的其他情况有锐角、有钝角,但这种情况4个都是直角。)
【思考】本環节通过两条直线的一次旋转运动将所有相交情况全部呈现,化零为整,再在抽象中引导学生发现旋转过程中的变与不变。在此基础上学生很容易体会出最特殊的相交情况,真正感受到垂直这一概念是包含于相交的。
二、变中求定,探索距离概念
学生已经掌握了两点之间线段最短,且线段只有一条。但点到直线的无数条线段里哪条最短?本环节放手让学生自主探究,边操作边思考,在变中求定,最终得出科学的结论。
【片段二:马里奥取水桶灭火】
师:(点A到点P)情况紧急,走哪一条?(生:线段,因为两点间线段最短。)(点P到直线ɑ)这回怎么走?比画一下。(生1横着比画:直着走最短。)还是走线段。(生2竖着比画:这条线段更短。)这回有不同的线段了,但从大家的回答里,我都听出一个共同的目的,都想走最短的线段。
师:刚才两点间线段最短,而且只有一条;现在,点到直线。有多少条线段?(生:无数条。)那有什么办法能在无数条里找出最短的?拿出桌上的学具,同桌一起,找到点到直线最短的线段,并画下来。注意:上面这根小棒是能左右摆动,可以比较点到直线各条线段的长短。
生1:我们把小棒从一边开始摆动,发现点到直线的线段先变短,然后又变长,所以在中间时最短。
生2:我们先把小棒从中间向左摆动,再从中间向右摆动,都很容易发现直线下方露出的小棒在变短,所以小棒在中间时下方露出最长,那这时候上方那段线段是最短的。
师:这条线段除了最短,还有什么特殊的?继续探究。(生:直线ɑ是互相垂直的,因为相交成直角。)这条线段我们就叫做点P到直线ɑ的垂直线段。
师:我们都说垂直线段最短。把这条垂直线段往左摆动,它离直线ɑ越来越远。这些线段还和直线ɑ垂直吗?(生:不垂直。)再从中间往右摆动呢?(生:离直线ɑ也越来越远,也不垂直。)
师:结合摆动和数据。我们发现点到直线,的确垂直线段最短。这样的垂直线段有几条?(生:只有一条)。因此,我们把垂直线段的长度,叫做点到直线的距离。
【思考】本环节在已有经验的基础上,让学生借助学具自主探究。通过摆动学具,学生用不同的方法来找出最短的线段,但答案始终唯一,在变中求定,由抽象到具体。并在此基础上继续探究还有什么特别之处。学生在研究了长度之后,自然会将方向转到位置关系上,从而发现,这是一条点到直线的垂直线段。再在验证中发现垂直线段只有一条。

