数学史料进课堂，文化浸润兴趣长

王国军

数学是自然科学的基础，有其自身完整、清晰的逻辑体系和准确、规范的表达体系，教师必须在课堂上牢牢“抓住”学生的眼和脑，让学生经历数学知识的形成和发展过程。为此，笔者结合数学史的相关素材，编成诗作应用于课堂，学生们对这种形式很感兴趣，学习数学的兴趣越来越浓了。

一、概述数学核心概念的发展简史，激发兴趣

函数是数学中的核心概念，函数从形成到完善经历了三百多年的时间。学生在初中阶段已经学习过函数的相关知识，也知道了与之相关的解析式、图像等表示方法。在高一阶段，该如何重讲函数呢？在讲解函数的概念时，笔者用一首诗开头：

莱氏创词欧氏简，概念发展三百年。

贝式欧变狄对应，清李善兰译数函。

翻阅数学史，可以清楚地看到，在函数概念的发展过程中有几个重要的时间节点及数学家。1692年，德国数学家、哲学家莱布尼茨用“function”表示函数，函数这个名词从此面世。但函数到底是什么，其内涵与外延还不清楚明了。1718年，瑞士数学家约翰·贝努利（莱布尼茨的学生）指出了函数的形式—函数要用一个式子表示—突出了函数的形式化特征。这可以称为函数概念发展的第一阶段。1755年，瑞士数学家欧拉指出函数的内容—变量及变化，并且用f （x）表示函数，函数的符号从此固定下来。这就是函数概念发展的第二阶段。这就是学生在初中学习过的函数的概念，这样函数的概念虽然模糊，但基本上建立起来了。德国数学家狄立克莱于1837年进一步指出函数概念的本质内涵，函数是建立在非空数集上的映射，函数的本质就是一种对应。这就是函数概念发展的第三阶段。1895年，清朝数学家李善兰将“function”译为“函数”，从此函数的概念进入我国，成为数学工作者的专用术语。

教材上对数学核心概念也有相应的补充，作为阅读材料出现。这部分内容因考试不考，教师往往不讲，学生自然也不会过多注意。笔者认为，这一部分应该引起教师的注意，这既是数学史的有机组成部分，也是数学文化的重要载体。通过这一板块的学习，学生可以从另一角度看数学，也有利于学生构建数学整体的知识系统。

二、评析数学概念产生历程的得失，激发动力

对数的发明是数学史上的重大事件，也是人类文明发展历程中的重要里程碑。笔者曾经询问过学生对数的简单历史，大部分学生对此不甚了解，不少学生因对数过于抽象且不好理解而产生了畏难情绪。笔者在讲解对数时，用这样的诗句开头：

天文航海算数繁，曾借三角化加减。

史萌纳得欧揭底，根式指对一幂涵。

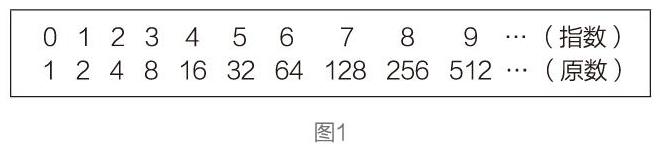
16、17世纪之交，随着天文观测和航海、工程、贸易以及军事的发展，解决大数运算的问题日益凸显，改进数字计算方法成了当务之急。16世纪前半叶，德国数学家约翰·维尔纳用三角函数的积化和差公式进行大数的计算，但对于大数的乘方与开方运算却没有好的解决方法，这就是前两句诗的内容。第三句涉及对数发展中的三个人，史提非、纳皮尔和欧拉。史提非天才地创造了两排数（见图1），将数的运算成功简化。比如，计算16×64的值，就在上排指数列中找到4和5两个数，相加得到9，再在下排原数列中找到9对应的数512，这就是16×64的计算结果。这就是对数产生的萌芽。1614年，纳皮尔用运动学、几何术语重新解释了上述原理，发明了对数。1624年，纳皮尔与布里格斯共同商定了以10为底的对数叫常用对数，公布了以10为底1～2000及90000～100000的14位常用对数表，极大地发展了对数的运算价值。1770年，大数学家欧拉用y=ax定义对数x=loga y，并指出对数源于指数，但对数的发明却早于指数（指数符号在1637年由法国数学家笛卡尔开始使用），成为数学史上的一大珍闻。

通過解读这首小诗，学生们既为史提非天才的创造所折服，又为其与对数的发明失之交臂而感叹;为纳皮尔另辟蹊径发明对数而感叹，又为其没有揭示对数的本质而遗憾;深深佩服数学大师欧拉的高瞻远瞩，又为对数最终有了数学的解释而兴奋。由认识到对数源于指数，学生自然而然地想到了用指数的运算性质对应记忆对数的运算性质，这样指数与对数的联系就更加紧密。这样处理教材，既减少了学生不必要的记忆量，又突出了数学概念间的天然联系，加之对历史人物得与失的感慨，学生怎么会没有学习数学的兴趣呢？

三、总结数学核心板块的公式系统，激励精神

三角函数部分由于有大量的公式需要记忆，学生对此颇有怨言：一怕公式记不准，二怕不能正确选择合适的公式。三角函数有一句流传甚广的记忆口诀—奇变偶不变，符号看象限。虽然此口诀言简意赅，减少了记忆量，但对诱导公式如何使用却没有交代。笔者在讲授“三角函数的诱导公式”时，先对课题里的“诱导”一词进行了新的解读，怎么诱呢？诱在这里就是凑角，用第一象限里的锐角α表示其他三个象限的角。用什么导呢？这里的导就是发现两个角对应的三角函数值的关系。成功引起学生的关注之后，笔者将三角函数的诱导公式分成两组进行解构，一组是保名变换，一组是改名变换。重点关注诱导前后三角函数名称和符号的变化，并利用单位圆结合对称性将公式改名与否、变号与否进行了解释和说明。在总结阶段，笔者抛出这样一首诗，作为本节课的结束：

三角化简先诱导，负角化正大变小。

奇变偶同定符号，圆中对称自明了。

笔者没有对这首诗做任何解释，当这首诗完整出现在黑板上时，正好下课铃声响起，同学们自发鼓掌，沉浸在数学学习的乐趣中。

教无定法，教无常法。在教学上从来没有一种方法包打天下。作为一种有益的尝试，笔者将数学史编成诗，将“数学诗”引入课堂，取得了很好的教学效果。笔者希望与更多的同行交流，也欢迎大家批评指正。

（作者单位：河北省石家庄市第二中学）

责任编辑：胡玉敏

huym@zgjszz.cn