0.005级压力式水深测量仪器检定装置的测量不确定度评定

王朋朋，程 杰，张艳昆，赵士伟，孟庆军

（32217部队，山东 烟台 264100）

1 引言

水深是重要的水文要素之一，压力测深是目前主要的测深原理。压力式水深测量仪器检定装置以准确度高、技术性能稳定、使用范围广等优点被用作压力计量的标准器。压力式水深测量仪器检定装置按照工作介质分为气体活塞压力测量仪器检定装置和液体活塞压力测量仪器检定装置，两者工作原理一致，但影响量有细微差别。评定其测量不确定度是压力计量人员的一项重要工作。李迪对活塞压力计标准进行了不确定度评定，着重分析了专用砝码的影响［1］；黄智渊等对气体活塞压力计进行了测量不确定评定［2，3］；李杨眉等对海洋压力测量仪器的校准结果进行了不确定分析［4，5］；其他学者还对活塞式压力计的活塞有效面积进行了大量研究［6，7］；李文博等用蒙特卡洛法对气压传感器进行检定结果的不确定度进行评定［8］。

上述研究工作主要针对单一工作介质的活塞压力计，多采用GUM法理论分析及针对单次测量结果的不确定度评定，没有对气体活塞压力计和液体活塞压力计的不确定度进行综合分析。据此，本文采用自适应MCM 和GUM 法分别对0.005级的气体活塞压力测量仪器检定装置和液体活塞压力测量仪器检定装置进行了测量不确定度评定，并通过自适应MCM 对GUM 法进行了验证。

2 压力式水深测量仪器检定装置测量原理

压力式水深测量仪器检定装置的主标准器是活塞式压力计。其主要是基于流体静力学原理和帕斯卡原理设计的，作为测量压力的标准装置，它由活塞系统、砝码和底座3部分组成。活塞式压力计的工作原理如图1所示。活塞系统工作时，活塞杆应稳定悬浮于活塞筒中并处于标称工作位置。此时作用于活塞底部向上的力F（F＝p×A，p为压强，A为活塞杆面积）与加于活塞上的砝码所产生的重力相平衡。被测压力可以由砝码所受重力和活塞杆面积计算，对于一定的活塞杆面积，改变砝码质量就可以测量不同的压力。为了避免产生静摩擦力，在工作时使活塞杆与活塞筒之间可相对旋转运动，从而使活塞杆处于活塞筒的标称工作位置，与活塞筒之间有一个均匀的介质层。

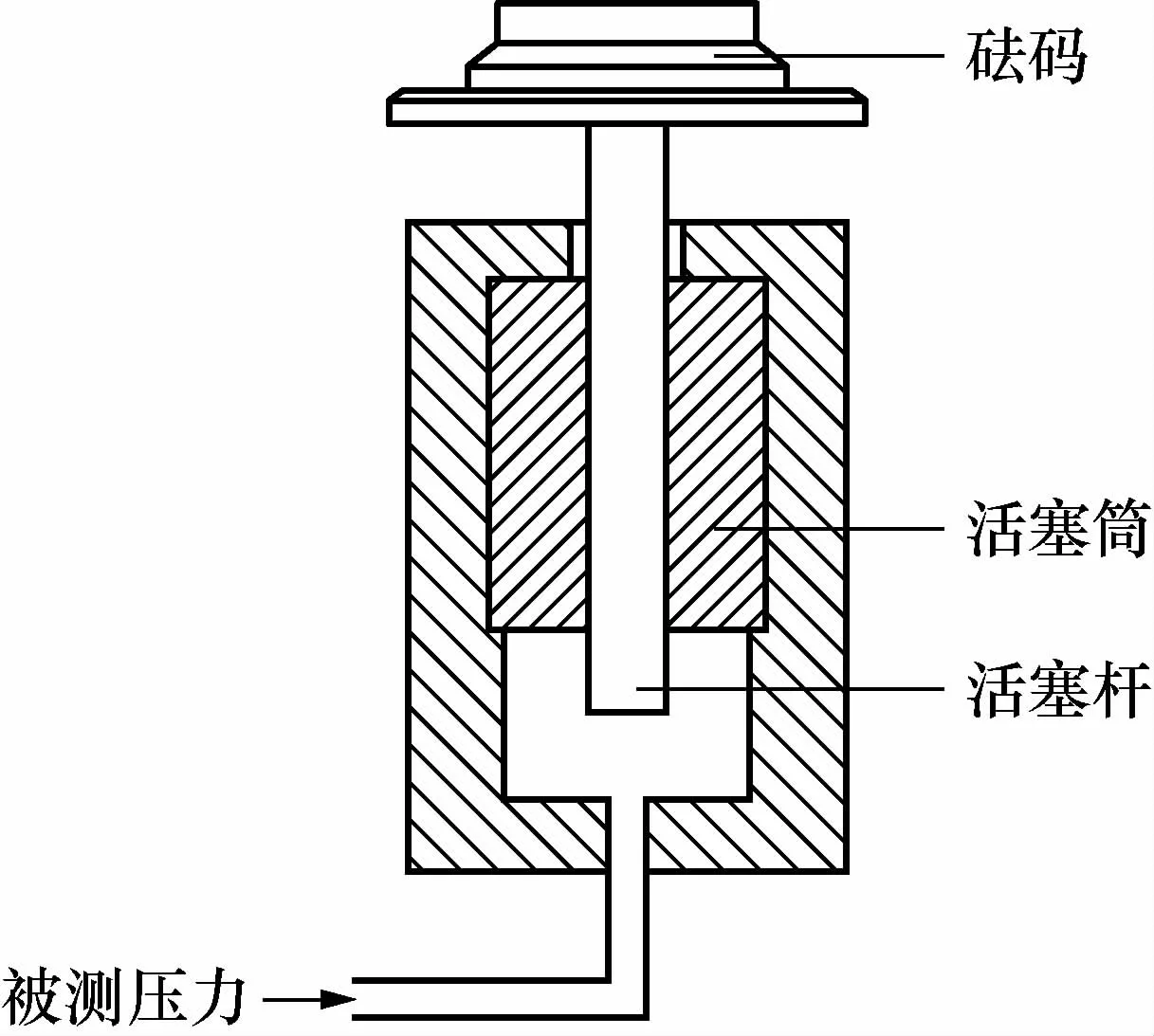
图1 活塞压力计工作原理图Fig.1 Working principle diagram of piston pressure gauge

根据活塞式压力计的工作原理知，其所测得的压力可由砝码质量和活塞面积共同表示。实际工作中，必须考虑活塞压力计的其他影响因素，通过修正使其对活塞压力计输出压力准确度的影响减到最小。这里面，需要考虑活塞压力计的温度变化以及压力形变的影响，应进行温度、压力形变修正，也要考虑工作介质的表面张力影响因素，还要对质量进行浮力修正。

当活塞处于工作位置时，活塞所产生（或者测量）压力的计算修正公式如式（1）：

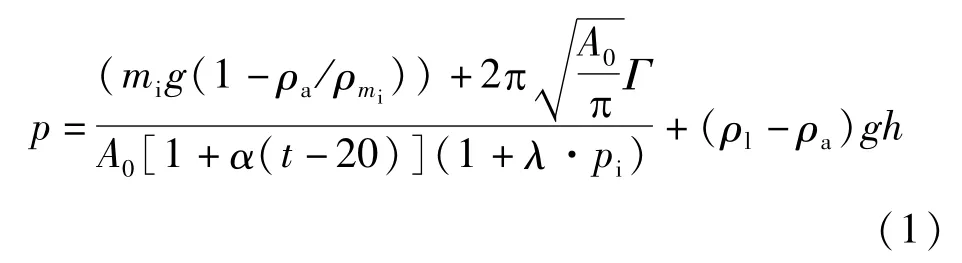
式中：A0为在参考温度和零压力下活塞系统的有效面积，m2；λ为压力形变系数，为常量，1／MPa；α为活塞组热膨胀系数，为常量，1／℃；t为活塞工作温度，℃；mi为压力测试点相应的活塞杆及专用砝码质量总和，kg；g为当地重力加速度，由于其实测误差仅为10－7量级，可取为常量，m／s2；ρa为空气密度，kg／m3；ρmi为砝码（或活塞、连接件、承重盘）密度，为常量，kg／m3；ρl为介质密度，kg／m3；Γ为活塞表面张力系数，N／m；pi为压力名义值，MPa；h为活塞参考平面与测量平面的差，m。

为了计算方便，对式（1）进行变换，令：

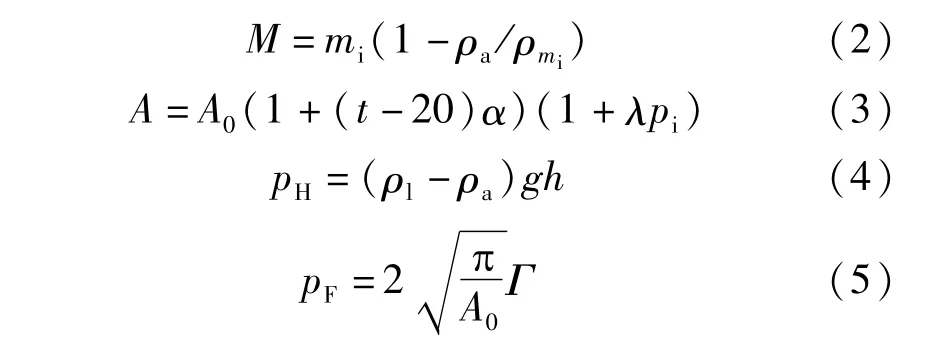
则有：

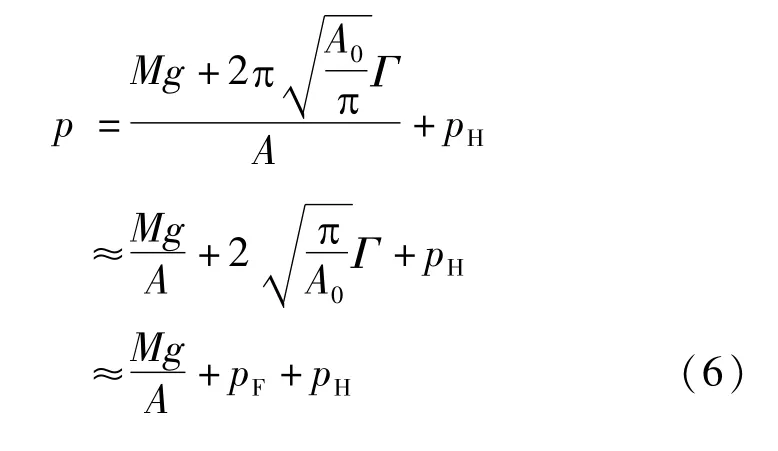
3 GUM法评定测量不确定度

3.1 数学模型

根据压力式水深测量仪器检定装置的测量原理，测量模型如式（1）所示。

3.2 测量不确定度评定

3.2.1 活塞及砝码组件质量误差引入的不确定度分量u（M）

活塞专用砝码以及活塞与连接件质量的不确定度是活塞压力计不确定度的重要来源，根据式（2），考虑影响量，可以得到灵敏系数：

根据不确定度传播率得：

以相对不确定度表示为：

（1）活塞以及活塞承重盘、专用砝码等的质量不确定度u（mi）

根据活塞压力计检定证书知，活塞及专用砝码允许误差为±0.001%，假设服从均匀分布则按B类不确定度评定，标准不确定度为：

用相对不确定度表示为：

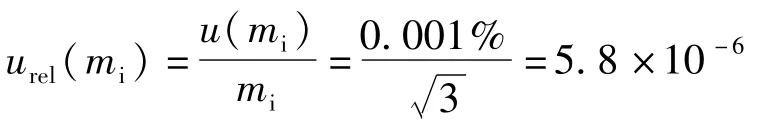
式中：mi为压力测试点相应的活塞杆及专用砝码质量之和，kg。

（2）空气密度的不确定度u（ρa）

我国空气密度范围为（1.2±0.05）kg／m3，假设服从均匀分布，k＝，则按B类不确定度评定，标准不确定度为：

用相对不确定度表示为：

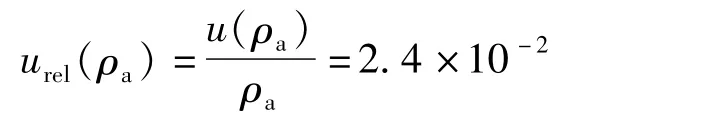
3.2.2 活塞有效面积引入的不确定度分量u（A）

根据式（3），得到灵敏系数：

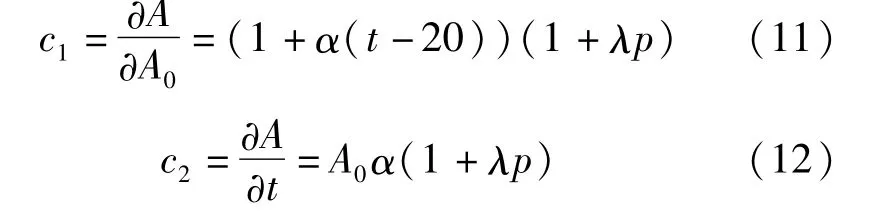
根据不确定度传播率得，

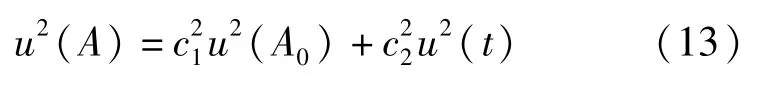
以相对不确定度表示为：

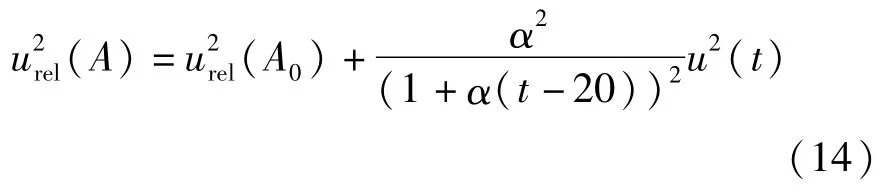
其中活塞系统的热膨胀系数α取决于活塞杆以及活塞筒的材料，对于某种材料而言，此项一般为常数，故引入的标准不确定度可以忽略；形变系数λ取决于活塞杆和活塞筒的材质以及结构，此项一般为常数，故引入的标准不确定度可以忽略。

（1）活塞在标准状态下有效面积A0的不确定度u（A0）

根据活塞压力计检定证书可知活塞面积的检定结果为（A0±ΔA）／cm2，假设活塞面积服从均匀分布，，则按B类不确定度评定，标准不确定度u（A0）／m2为：

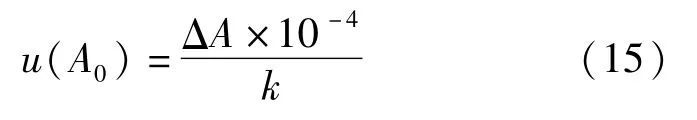
以相对不确定度表示为：

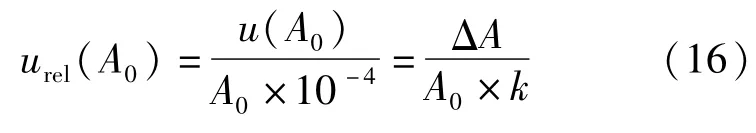
（2）活塞温度测量的标准不确定度u（t）

在活塞工作时，由于摩擦等因素会使活塞系统温度上升。这时，测量活塞的温度然后对于活塞有效面积进行温度修正是必须的。根据活塞压力计的使用说明书，温度误差±0.2℃（20℃时），假设服从正态分布，k＝2，则按B类不确定度评定，标准不确定度为：

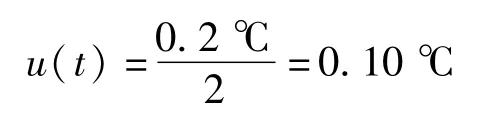
以相对不确定度表示为：

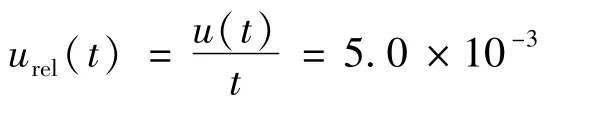
3.2.3 工作介质表面张力引入的不确定度u（pF）

表面张力对于液体介质的活塞有影响，对于纯气体介质活塞可以忽略不计。

根据表面张力计算式（5），可得到灵敏系数为：

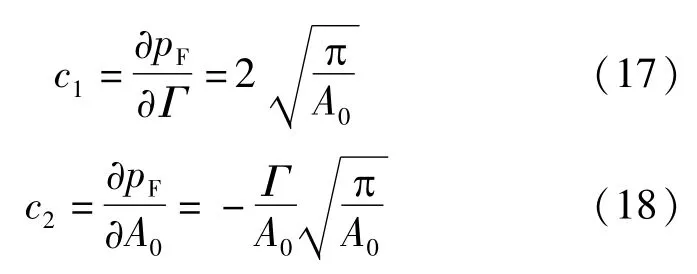
根据不确定度传播率得：

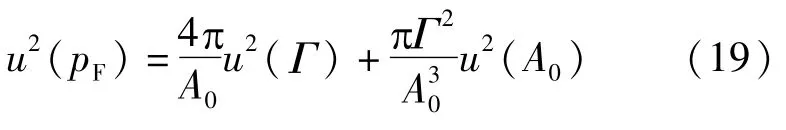
以相对不确定度表示为：

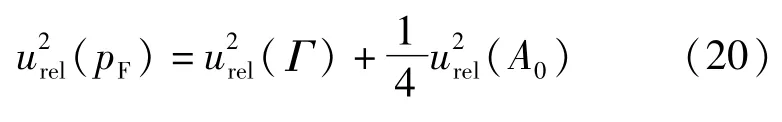
（1）活塞表面张力系数的不确定度u（Γ）

使用的测压介质，其张力系数在30 mN／m左右，其不确定度主要由温度变化造成，变化范围为25～35 mN／m。

假设服从均匀分布，k＝，则按B类不确定度评定，标准不确定度为：

以相对不确定度表示为：

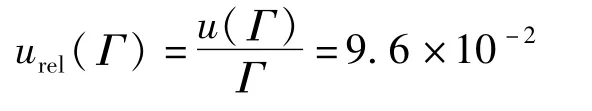
（2）活塞在标准状态下有效面积的不确定度u（A0）

活塞有效面积引入的不确定度u（A0）如前面所述。

3.2.4 与活塞工作位置的位置差带来的不确定度u（pH）

根据压差计算式（4），可得到灵敏系数：

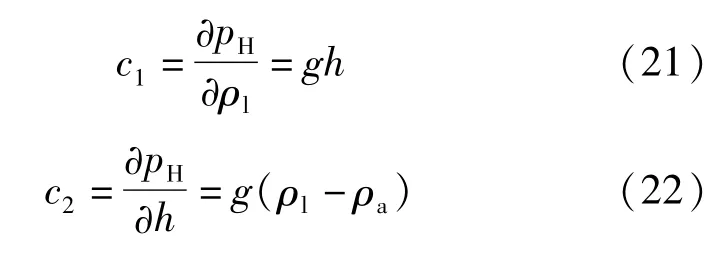
根据不确定度传播率得，

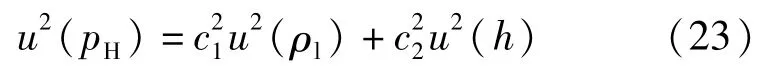
以相对不确定度表示为：

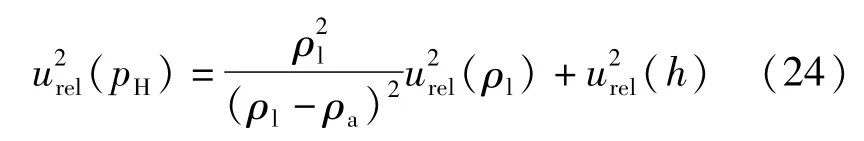
（1）气／液柱差不确定度u（h）

根据活塞压力计使用说明书，活塞的工作位置为0±Δhmm，其中气体活塞压力计为0±2 mm，液体活塞压力计为0±1 mm。设服从均匀分布，k＝，则按B类不确定度评定，标准不确定度为：

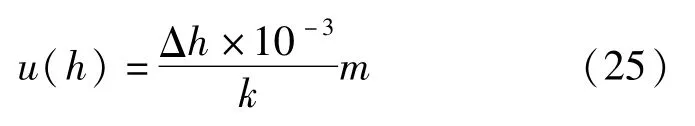
（2）介质密度的不确定度u（ρl）

如果介质是气体，由于气体的可压缩性，在进行高度差修正时应考虑不同压力检定点介质密度的变化，对于氮气可以采用式（26）计算其密度。

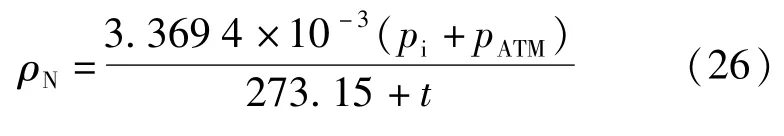
式中：pATM为当地大气压，Pa。

根据不确定度传播率，标准不确定度为：

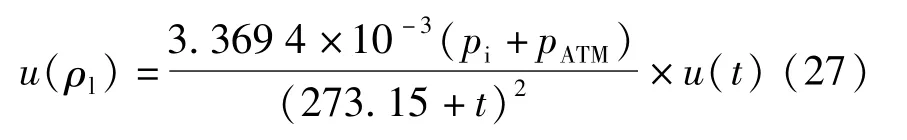
以相对不确定度表示为：

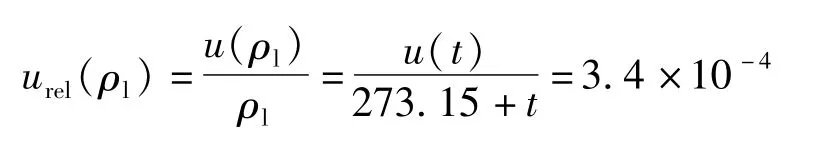
对于液体，其可压缩性较小，近似为常数，不确定度可以忽略，即u（ρl）＝0。

3.2.5 活塞轴线垂直度θ带来的不确定度u（pθ）

活塞的安装以及活塞本身结构有可能造成活塞轴线的不垂直，从而使加在活塞有效面积上的力小于活塞杆以及砝码所产生的重力。如果θ为轴线倾斜角度，那么轴线倾斜可能带来的影响量即为（1－cosθ）pi。规程规定，活塞安装垂直度要小于2′。假设服从均匀分布，k＝，则按B类不确定度评定，标准不确定度u（pθ）／Pa为：

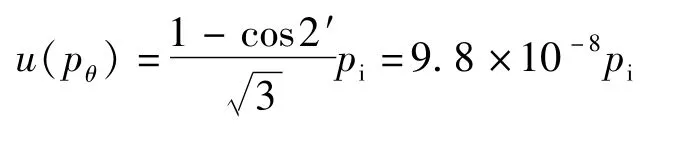
以相对不确定度表示为：

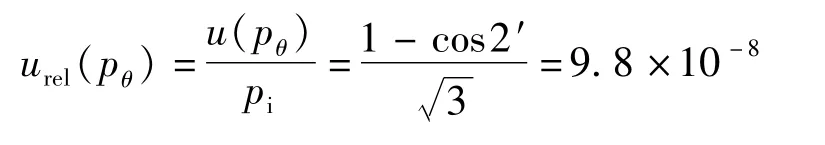
3.2.6 活塞压力计分辨力的影响u（r）

根据活塞压力计的使用说明书，气体活塞压力计的分辨力r＝1×10－3Pa，液体活塞压力计的分辨力r＝1 Pa，假设服从均匀分布，k＝，则按B类不确定度评定，标准不确定度u（r）／Pa为：

3.2.7 压力标准装置的测量重复性引入的不确定度uA

压力标准装置在各个检测点重复测试10次，测量重复性的不确定度分量用不确定度的A类评定方法得到。根据压力标准装置的重复性实际计算结果可以忽略不计。

3.3 合成标准不确定度

根据不确定度的传播率得，压力测量标准的合成标准不确定度用式（29）计算。

各压力测试点的合成标准不确定度见表1～3。

3.4 扩展不确定度

取置信因子k＝2，扩展不确定度根据式（30）计算得出。

各个压力测试点的扩展不确定度见表1～3。

表1 标准不确定度一览表Tab.1 List of standard uncertainty

表2 气体活塞压力计不确定度列表Tab.2 List of gas piston pressure gauge uncertainty

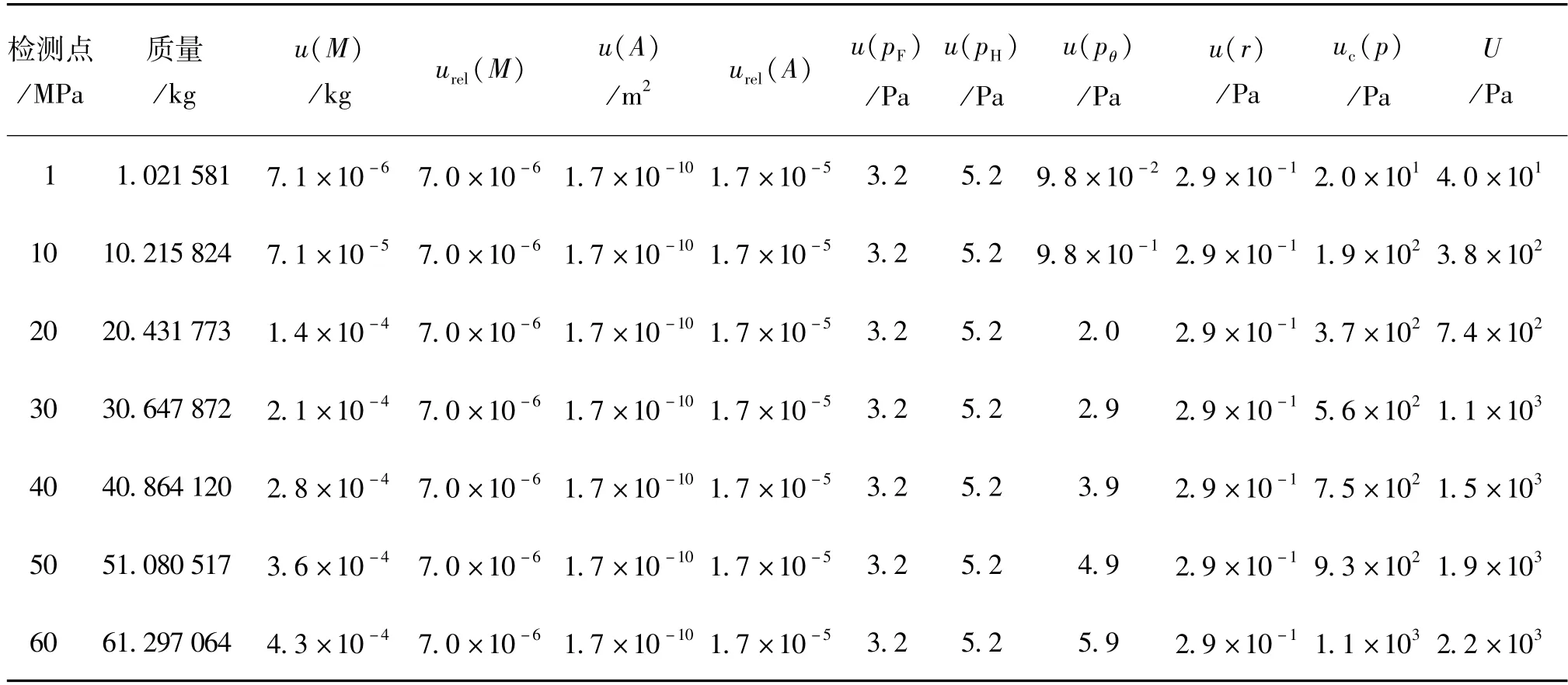
表3 液体活塞压力计不确定度列表Tab.3 List of liquid piston pressure gauge uncertainty

4 自适应MCM评定测量不确定度

根据压力测深的原理，建立的测量模型如式（1）所示。

每个输入量都由一个概率密度函数（PDF）表征，PDF由输入量的信息推导得到。表4为所有输入量及设定的PDF。

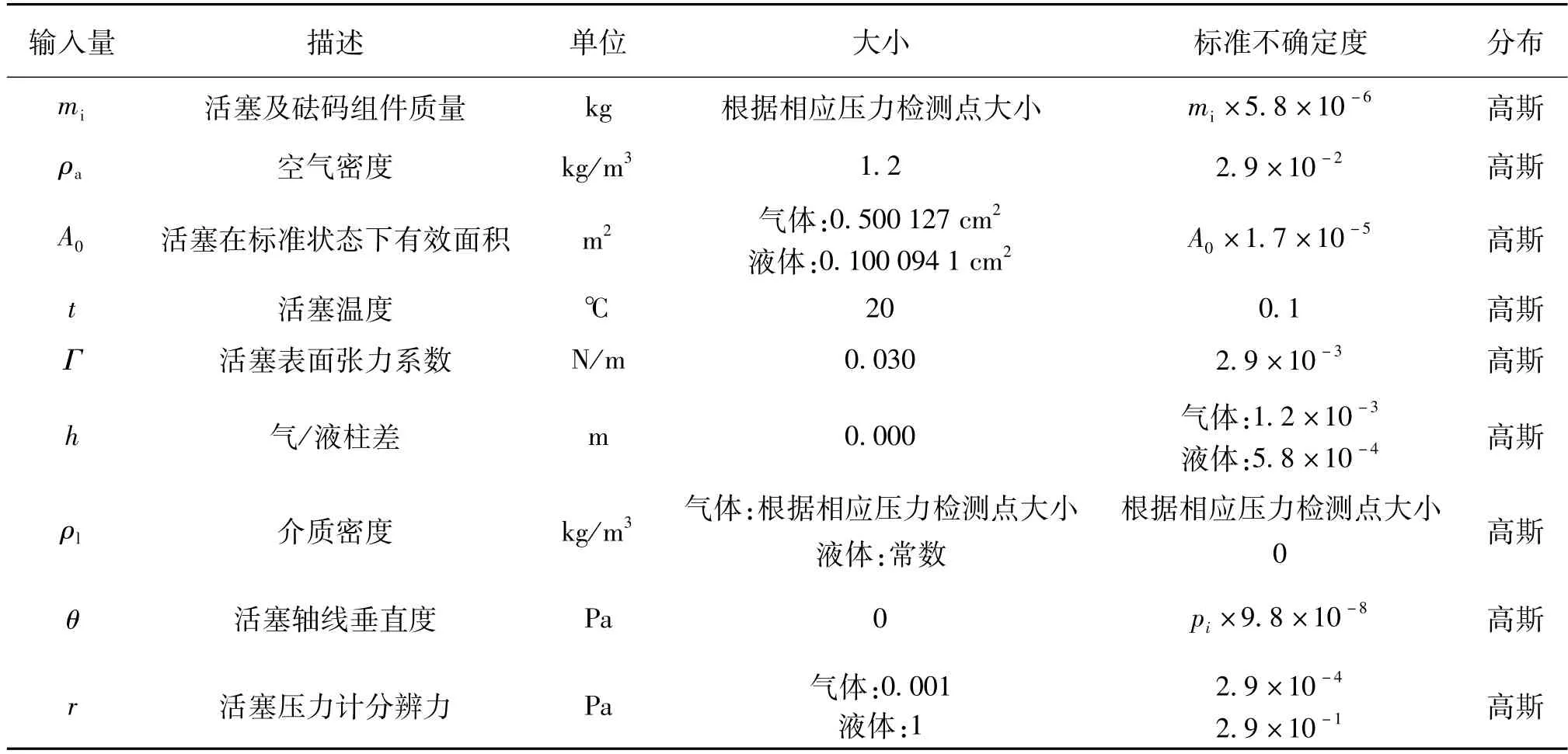
表4 输入量的大小、不确定度和设定分布列表Tab.4 Input size，uncertainty，and set distribution

根据自适应MCM的步骤［9～13］，编程得到满足条件的各输入量的随机数，取标准不确定度的有效数字位数为1位，当标准不确定度的有效数字首位为1或2时，给出2位有效数字［14］，确定数值容差δ，运用自适应MCM获得压力的估计值p、标准不确定度u（p）及在约定包含概率为95%时的包含区间。

对GUM法和自适应MCM获得的包含区间进行比较，当满足式（31）和式（32），则GUM不确定度框架可通过验证，结果见表5和表6。

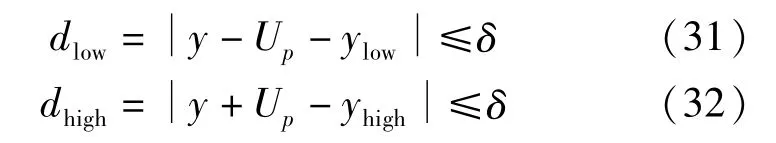
由表5和表6可知，自适应MCM与GUM法给出的气体活塞压力计和液体活塞压力计的压力估计值和标准不确定度具有很好的一致性，且各个检测点GUM法均验证通过。

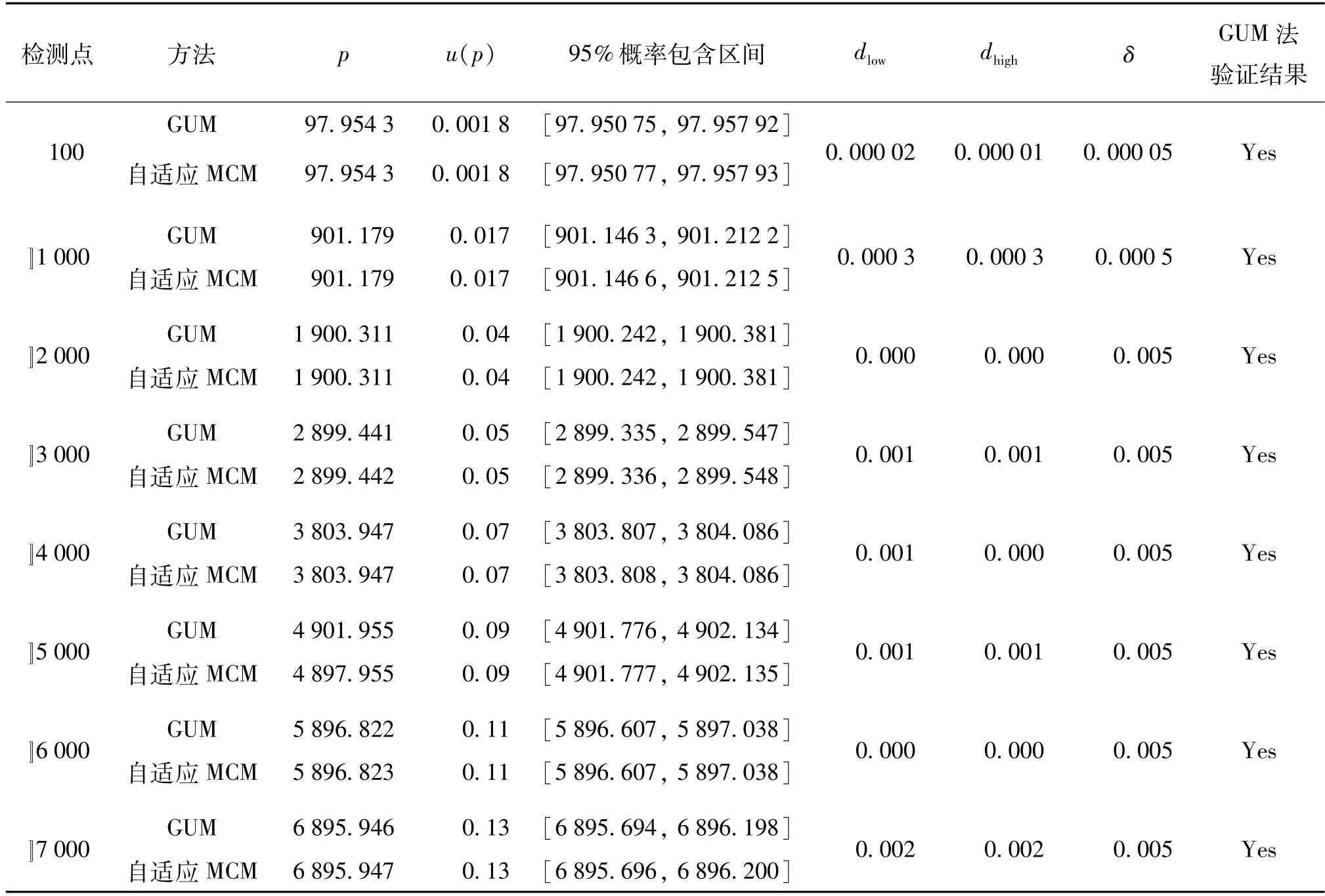
表5 气体活塞压力计自适应MCM与GUM法结果对比列表Tab.5 Comparison of adaptive MCM method and GUM method for gas piston pressure gauge kPa

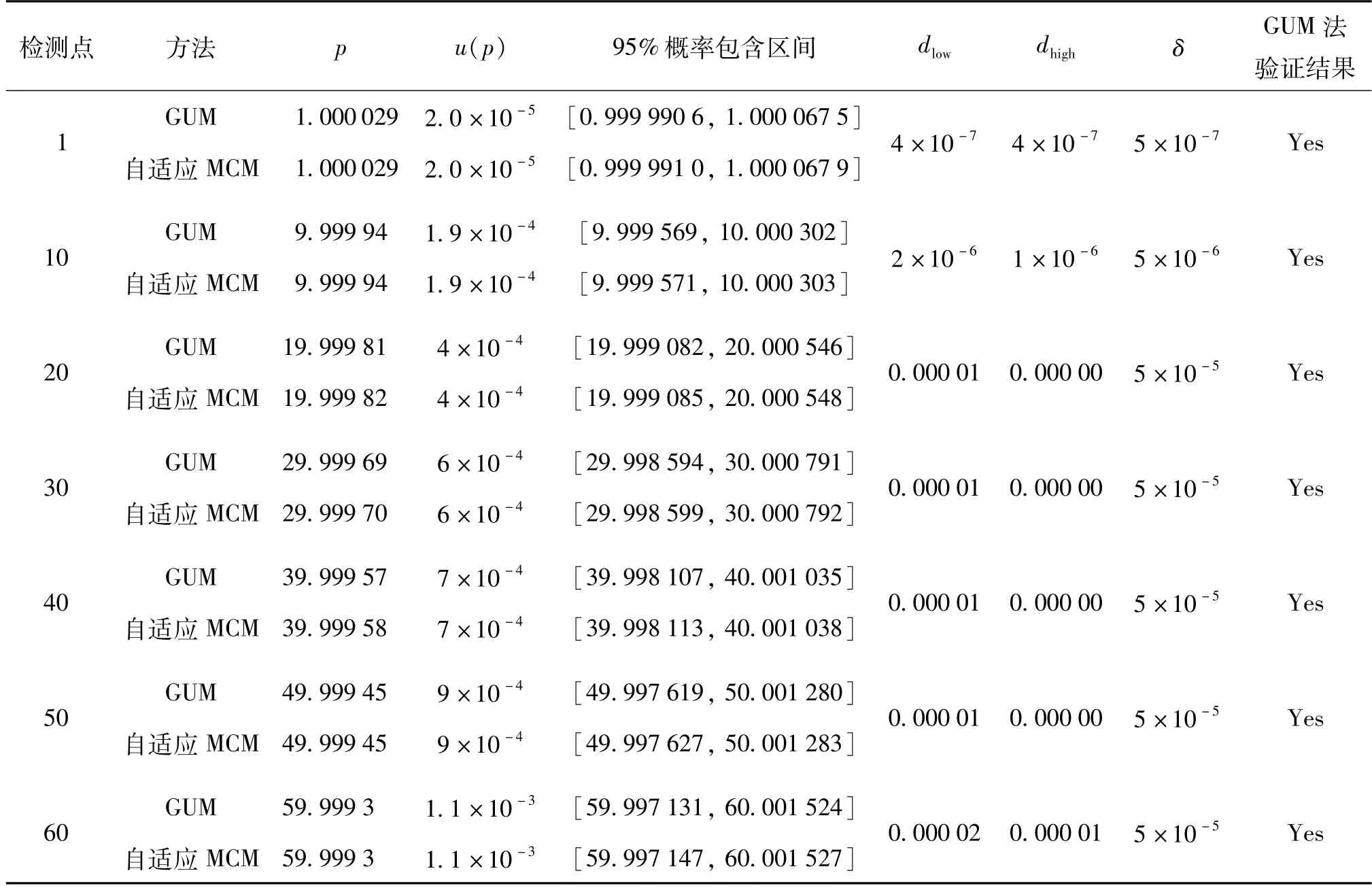
表6 液体活塞压力计自适应MCM与GUM法结果对比列表Tab.6 Comparison of adaptive MCM method and GUM method for liquid piston pressure gauge MPa

在验证过程中发现，当标准不确定度取两位有效数字时，气体活塞压力计在5 000 kPa测试点、液体活塞压力计在40 MPa和50 MPa时GUM法均未通过验证。因此合理的数值容差取值非常重要，实际测试中，测量结果位数的选取应考虑仪器的测量精度和使用要求，还要考虑标准仪器的标准不确定度的有效位数。

5 结论

本文分别采用GUM 法和自适应蒙特卡洛法（自适应MCM）对压力式水深检定装置进行不确定度评定，并使用自适应蒙特卡洛法对GUM法进行了验证。结果表明，虽然压力测量模型比较复杂，两种方法均适合用来评定其测量不确定度，并且在标准不确定度有效位数取1位时，GUM法在各个检测点均通过了验证，但自适应蒙特卡洛法适用条件更广泛，精确度也更高。采用自适应蒙特卡洛法对GUM法进行验证时，标准不确定度有效位数的选择对验证结果影响很大，取两位有效数字时，有些检测点没有通过验证。经分析，自适应程序中判断收敛的判据为数值容差，数值容差的大小与标准不确定度的有效位数有关，一般为一个很小的数，其大小反映了实际测量中的准确性和不确定度评定的可靠性，没有通过验证的检测点的标准不确定度和压力估计值在自适应MCM和GUM法时虽然具有较好的一致性，但在数值容差较小（有效数字为2位）时没有通过验证，在放宽了数值容差（有效数字取1位）后验证通过，因此数值容差取值的合理性很重要。